0115-不同的子序列

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 10:42:28 2023-09-13 10:42:28 Updated    

给你两个字符串 s **** 和 t ，统计并返回在 s 的 子序列 中 t 出现的个数，结果需要对 109 + 7 取模。

示例 1：

**输入：** s = "rabbbit", t = "rabbit"
**输出** **：**3
**解释：**
如下所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。
**_rabb_** b ** _it_**
**_ra_** b ** _bbit_**
**_rab_** b ** _bit_**

示例 2：

**输入：** s = "babgbag", t = "bag"
**输出** **：**5
**解释：**
如下所示, 有 5 种可以从 s 中得到 "bag" 的方案。 
**_ba_** b _ **g**_ bag
**_ba_** bgba ** _g_**
_**b**_ abgb ** _ag_**
ba _ **b**_ gb _ **ag**_
babg ** _bag_**

提示：

  • 1 <= s.length, t.length <= 1000
  • s 和 t 由英文字母组成

方法一：动态规划

假设字符串 $s$ 和 $t$ 的长度分别为 $m$ 和 $n$。如果 $t$ 是 $s$ 的子序列，则 $s$ 的长度一定大于或等于 $t$ 的长度，即只有当 $m \ge n$ 时，$t$ 才可能是 $s$ 的子序列。如果 $m<n$，则 $t$ 一定不是 $s$ 的子序列，因此直接返回 $0$。

当 $m \ge n$ 时，可以通过动态规划的方法计算在 $s$ 的子序列中 $t$ 出现的个数。

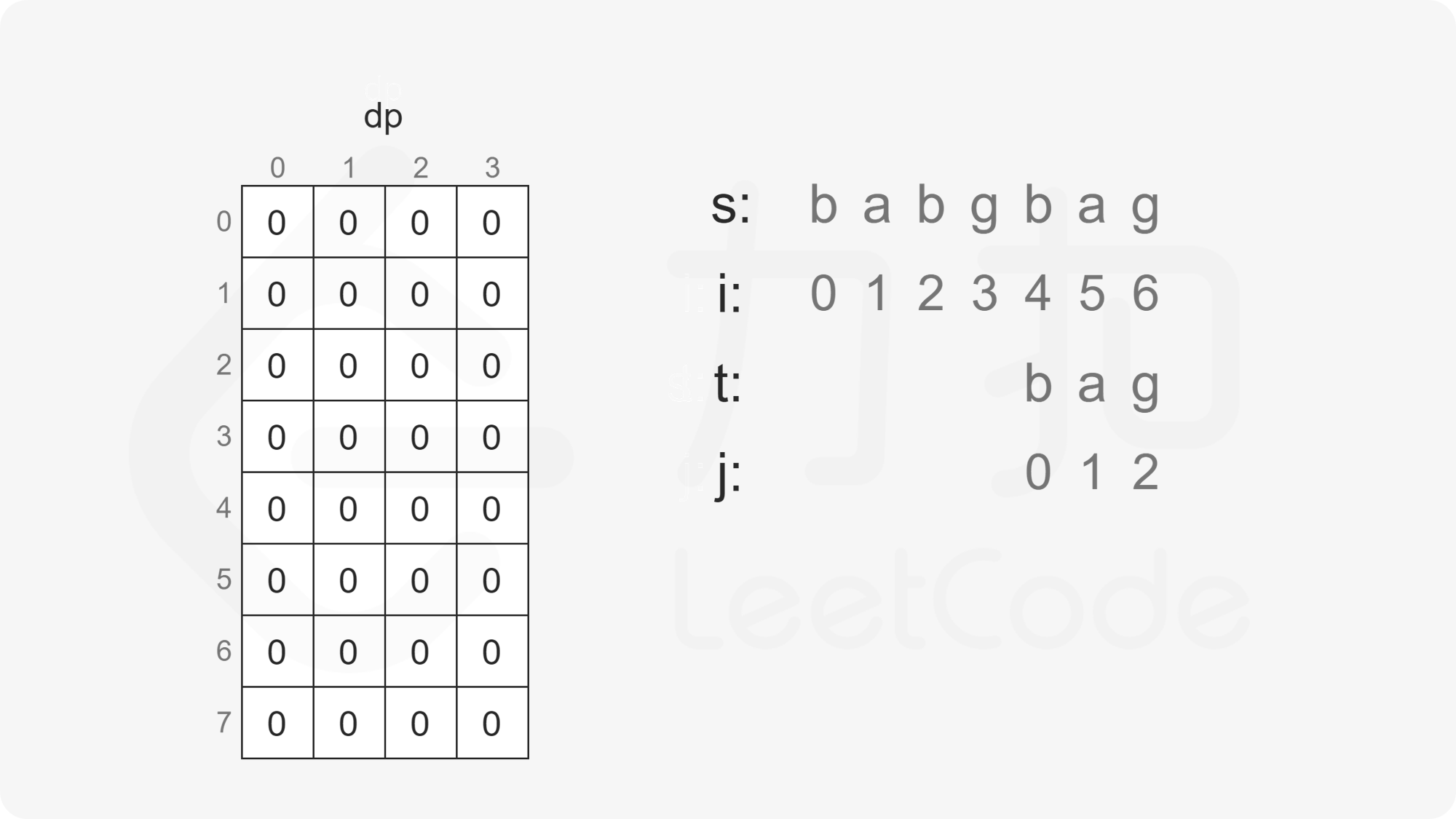
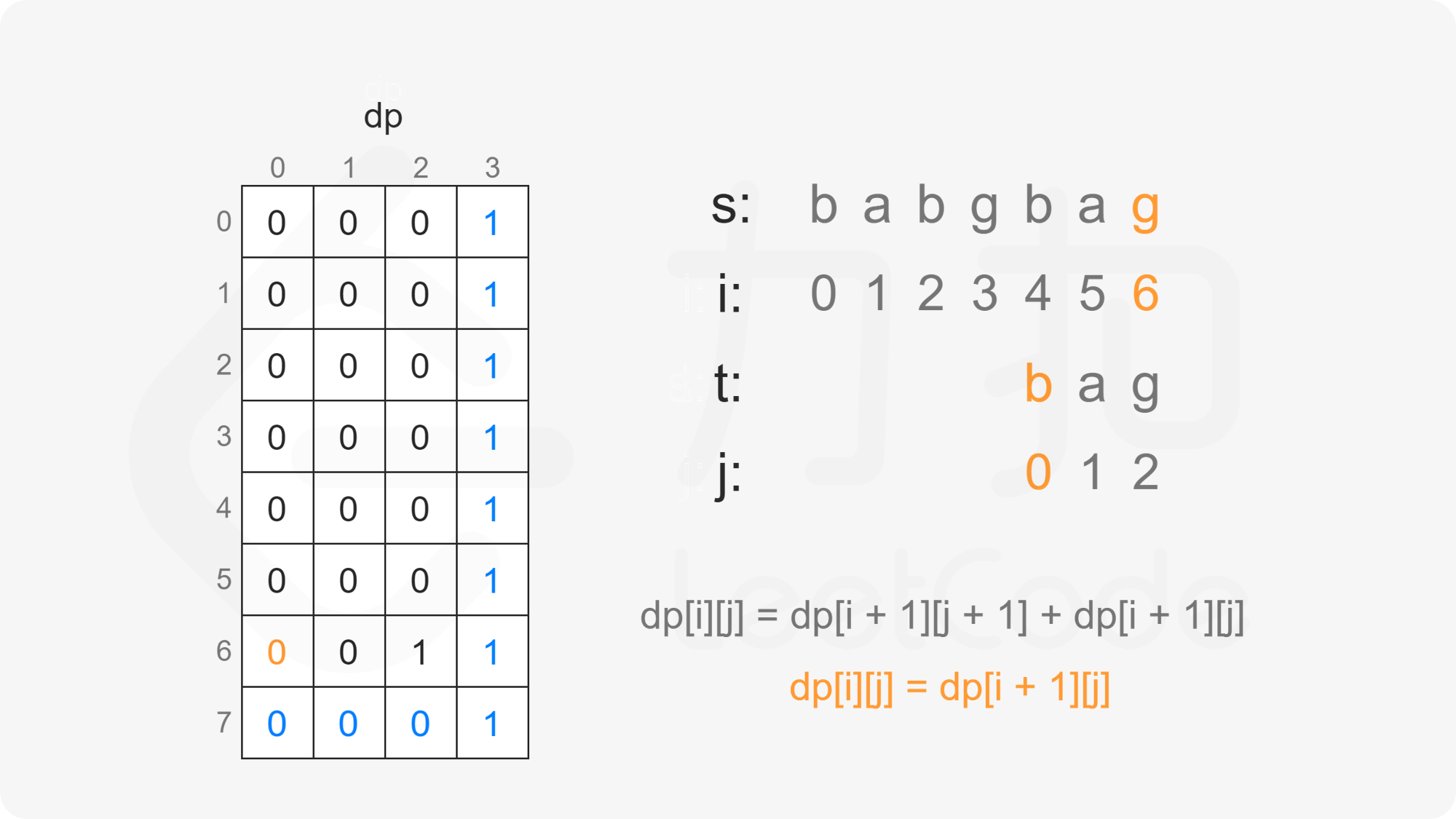
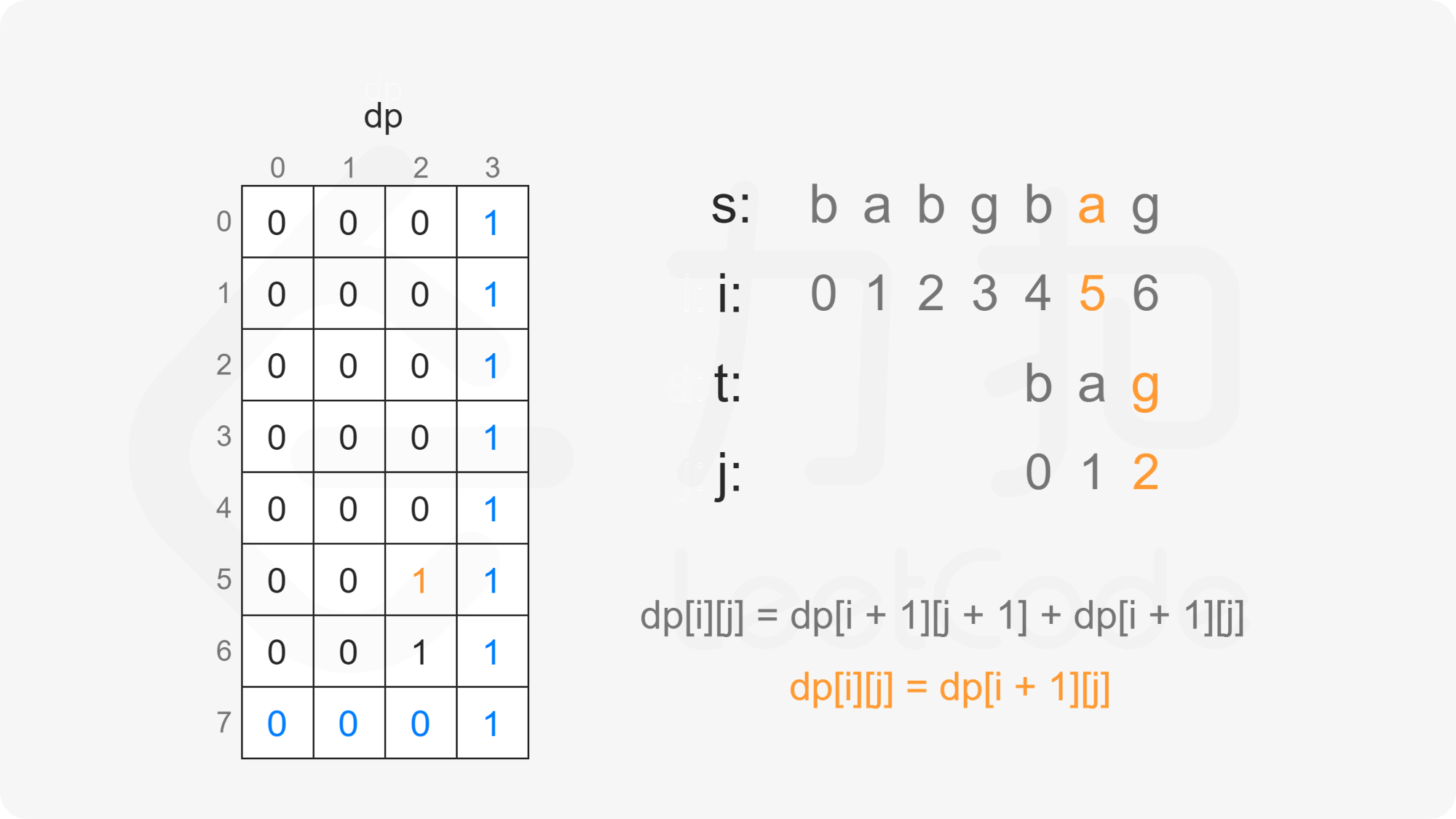
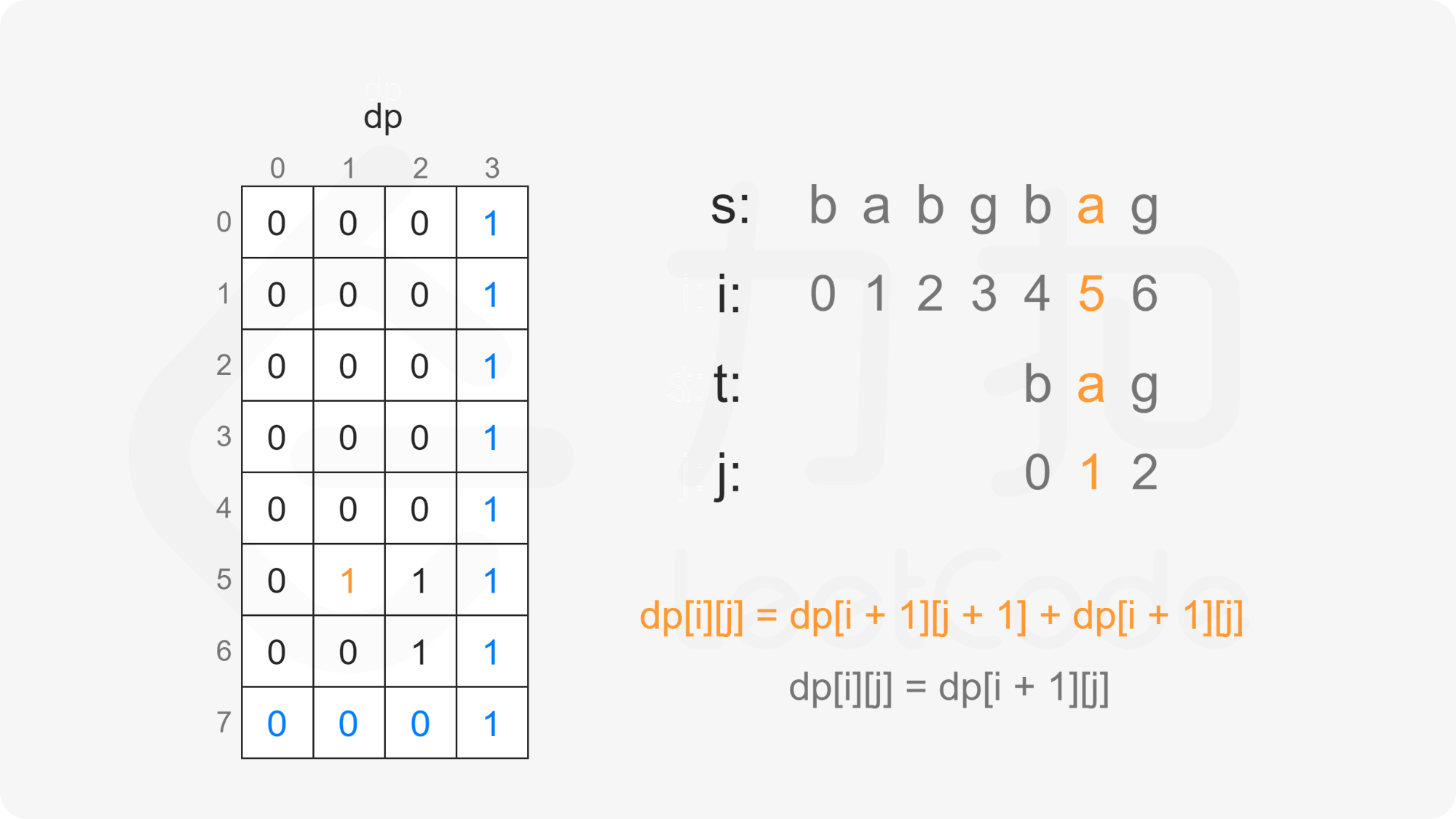
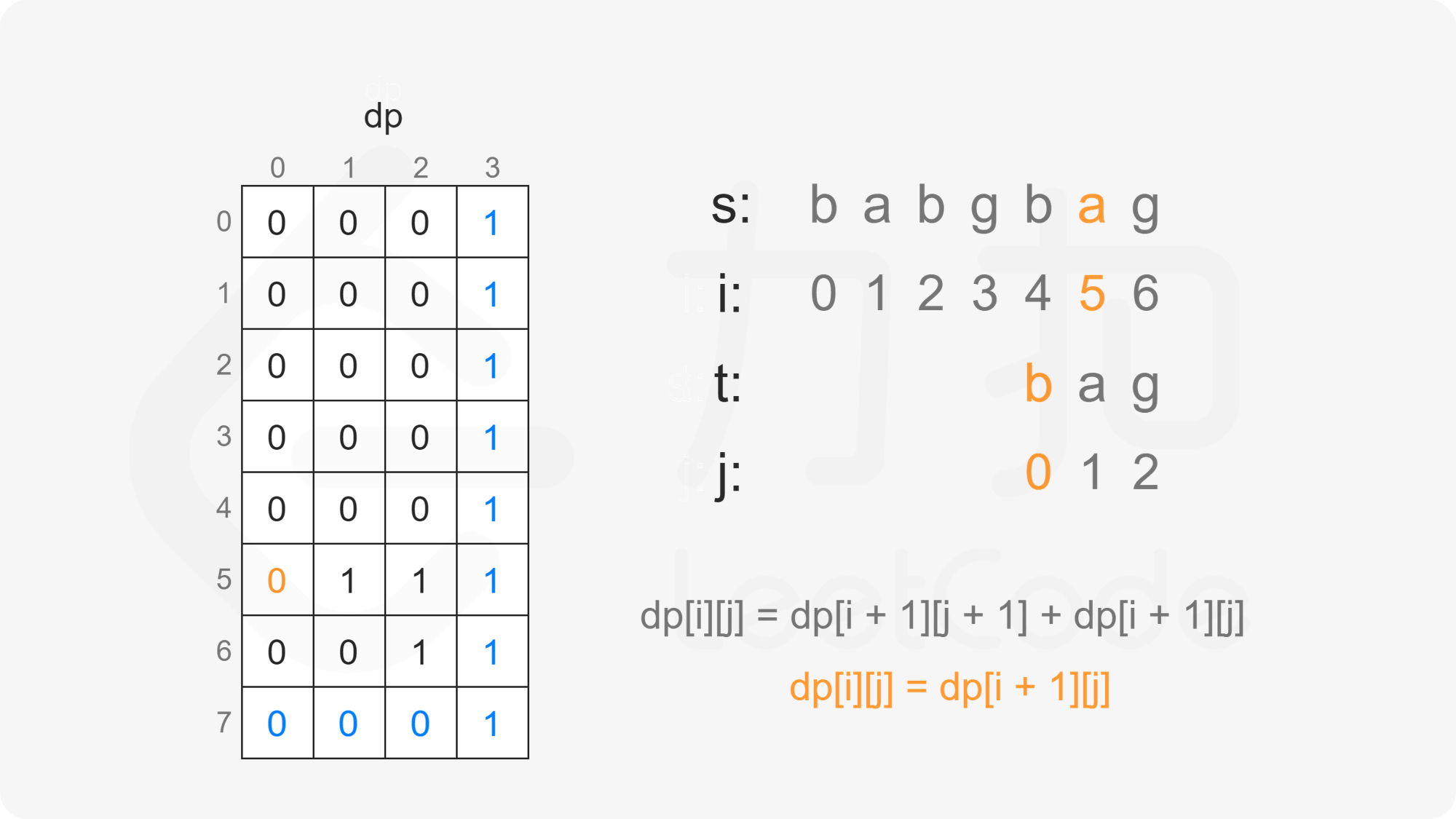
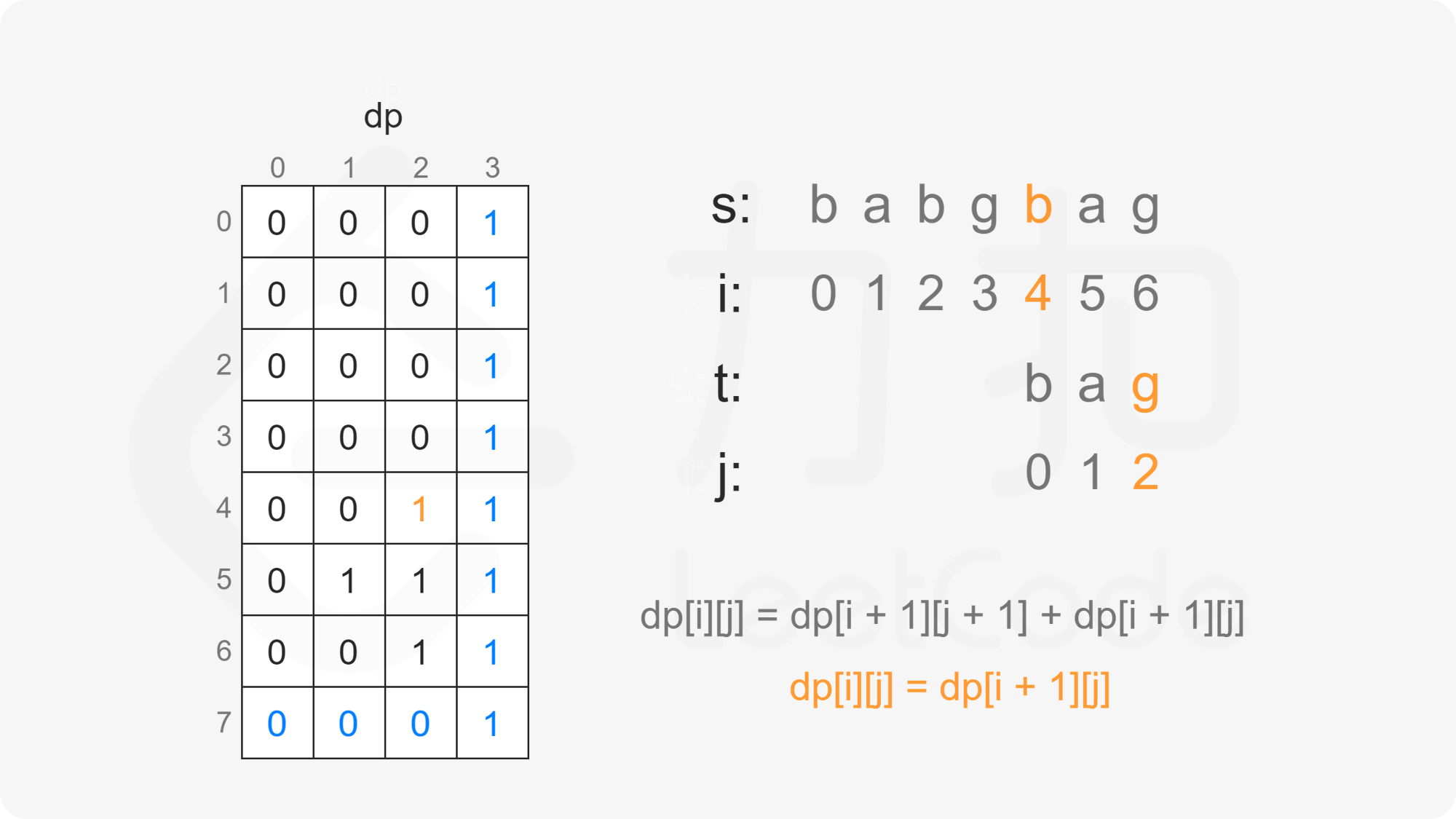
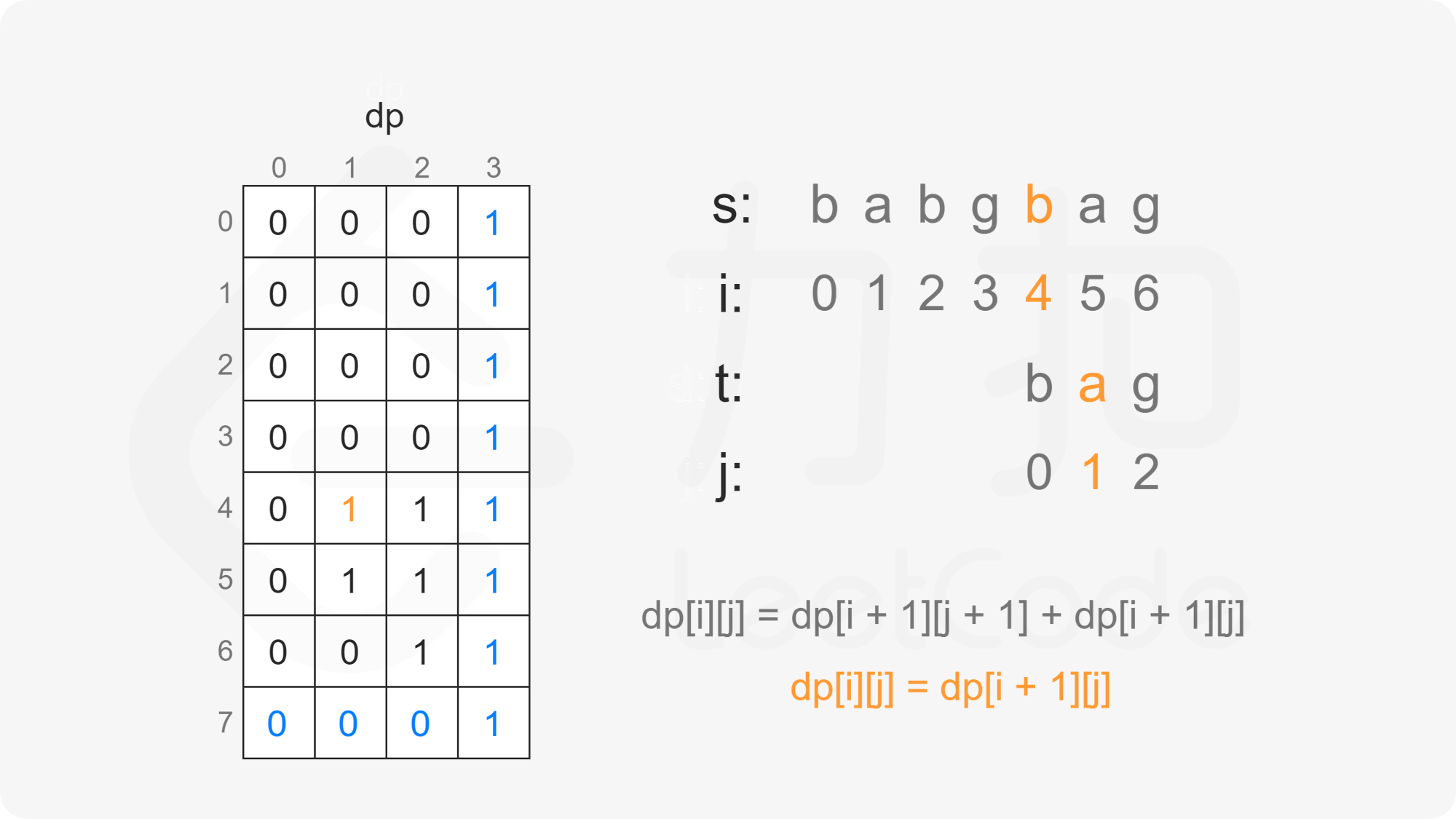
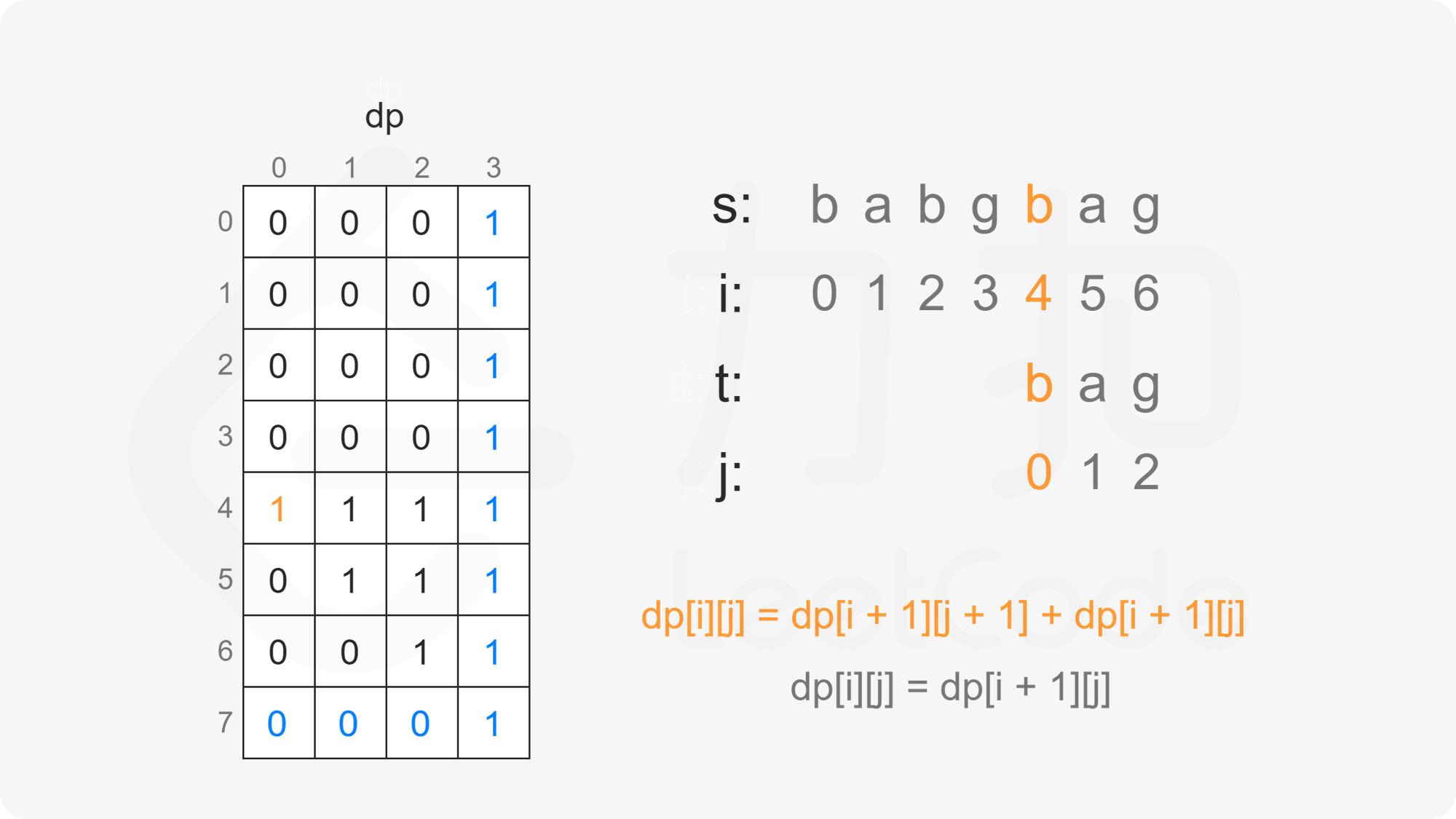
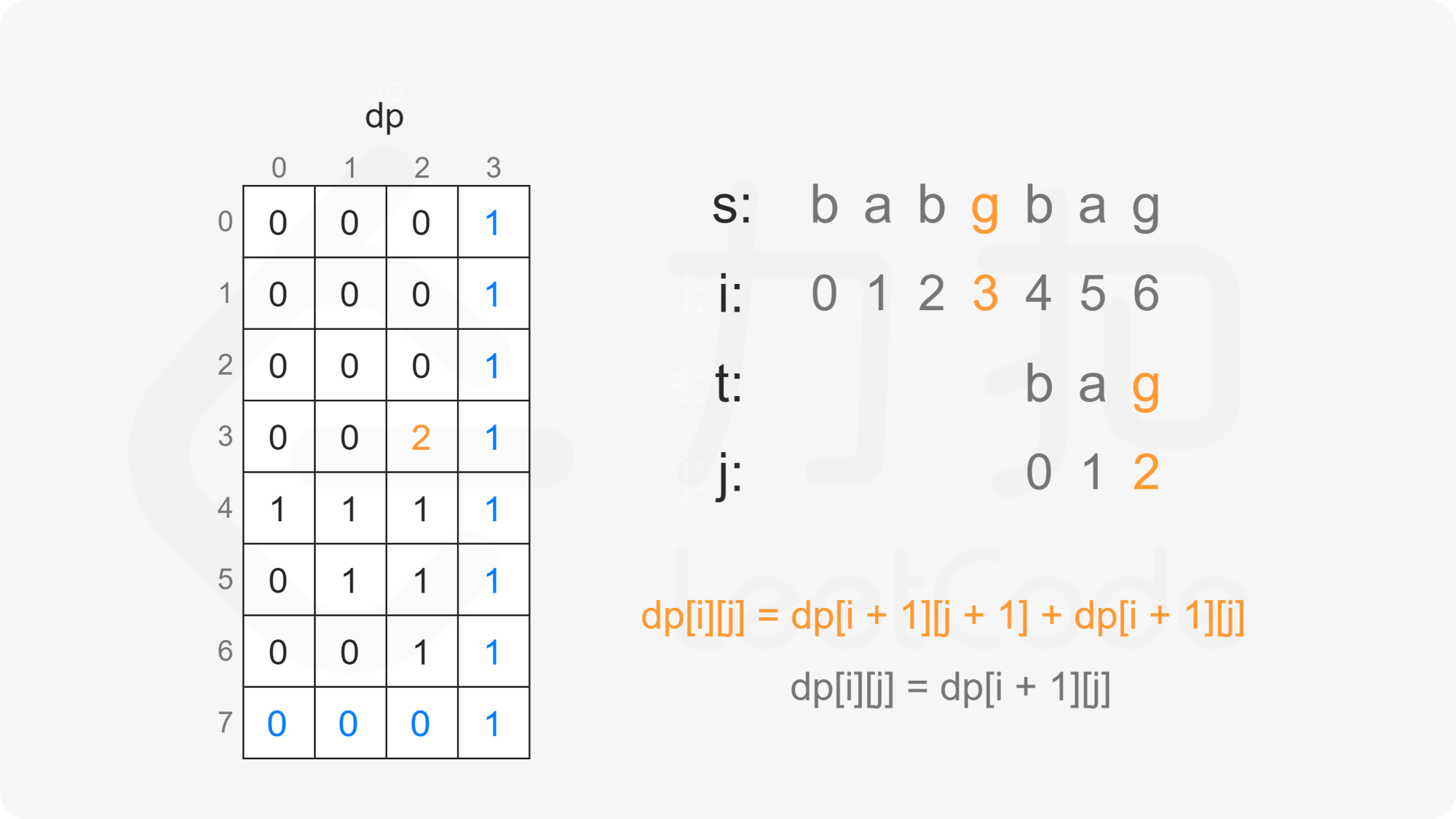
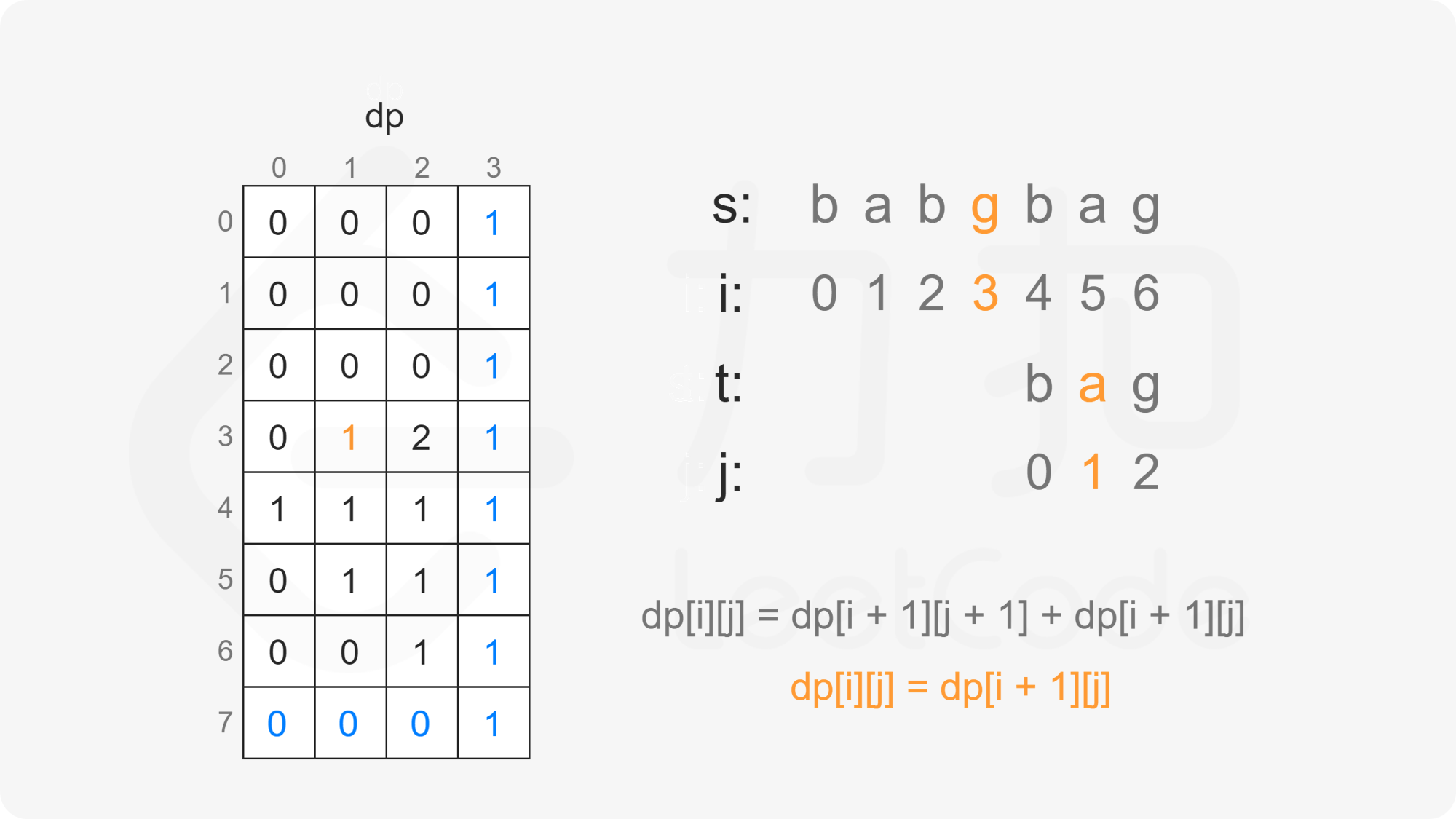
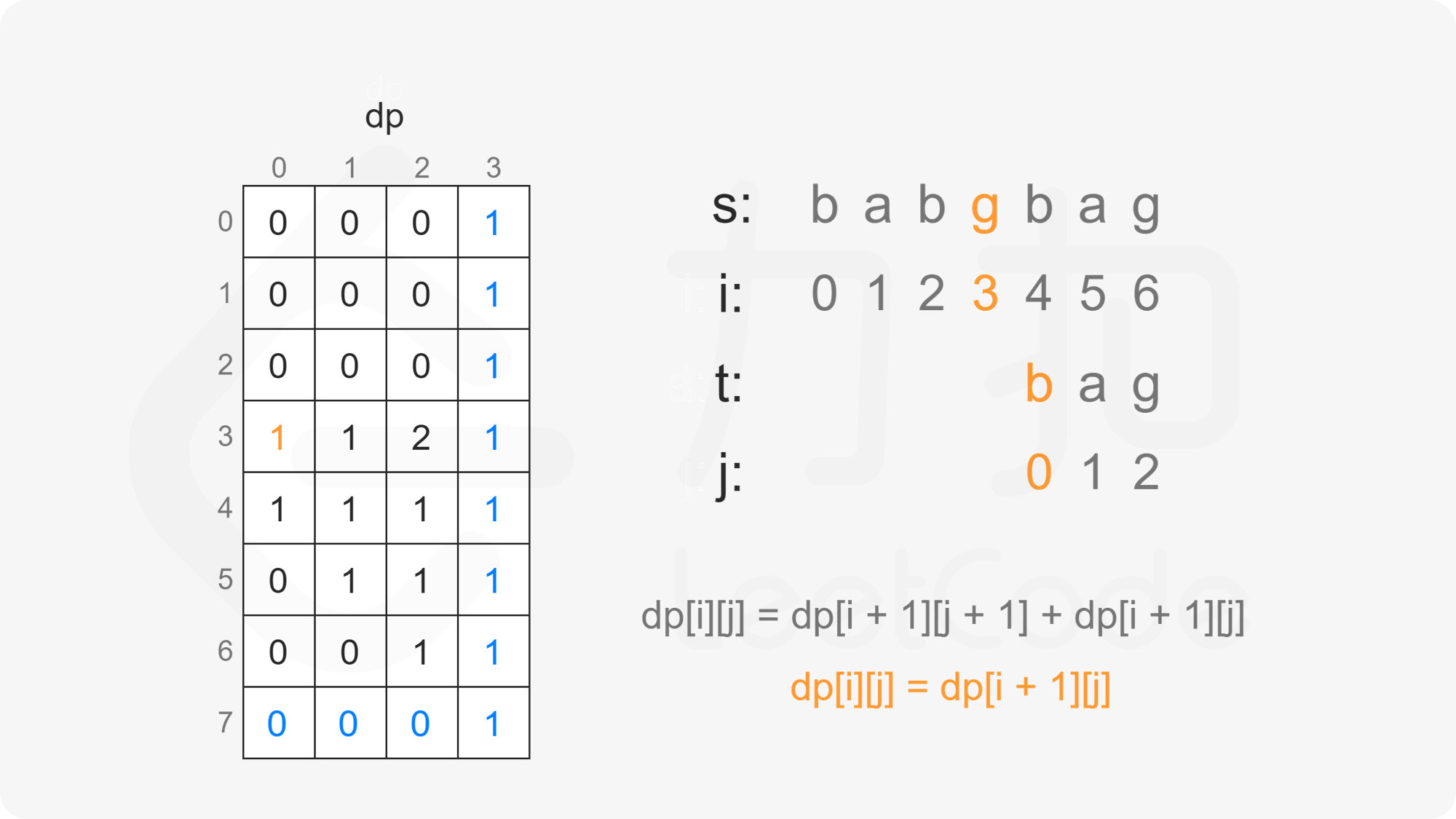
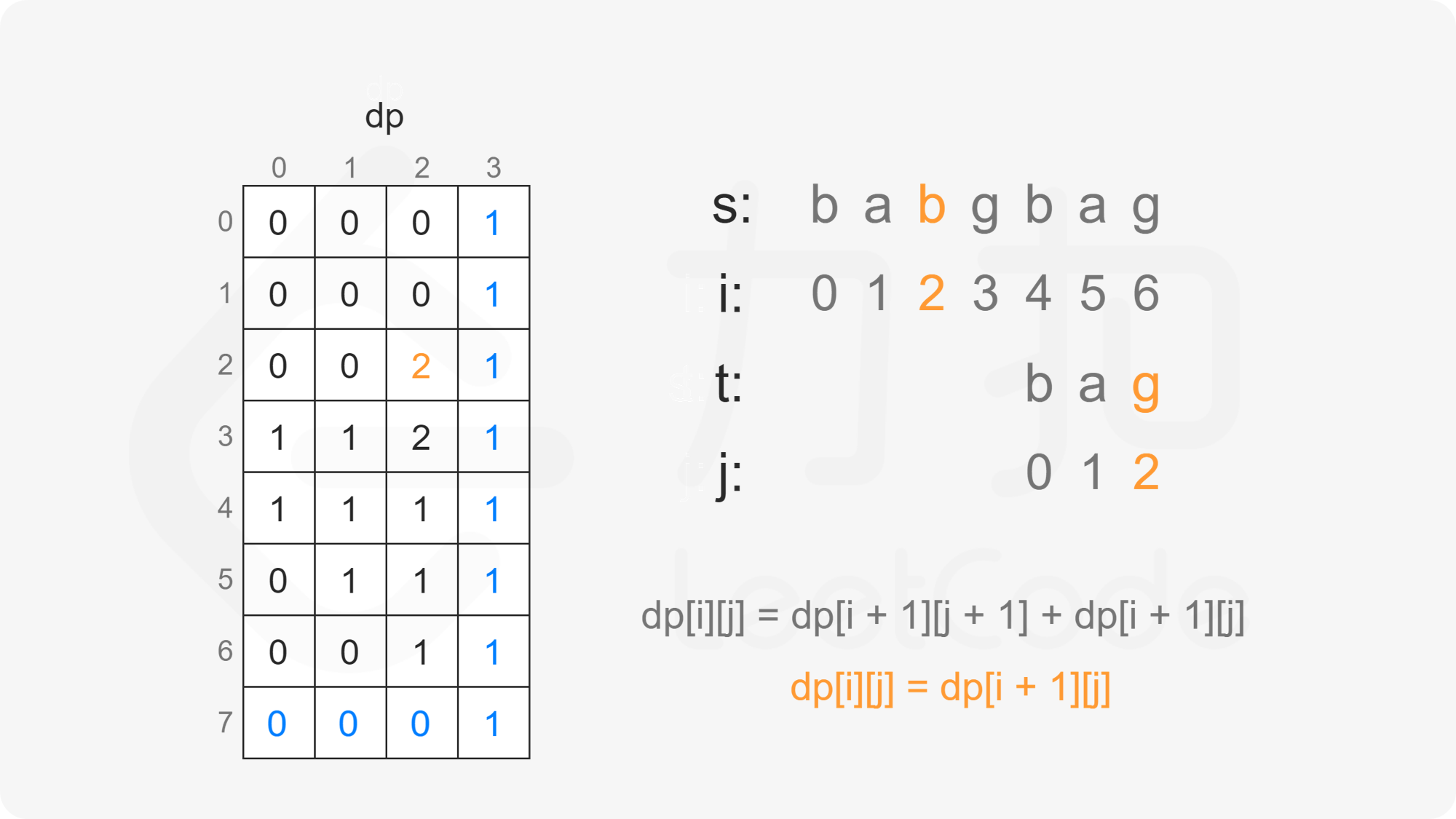
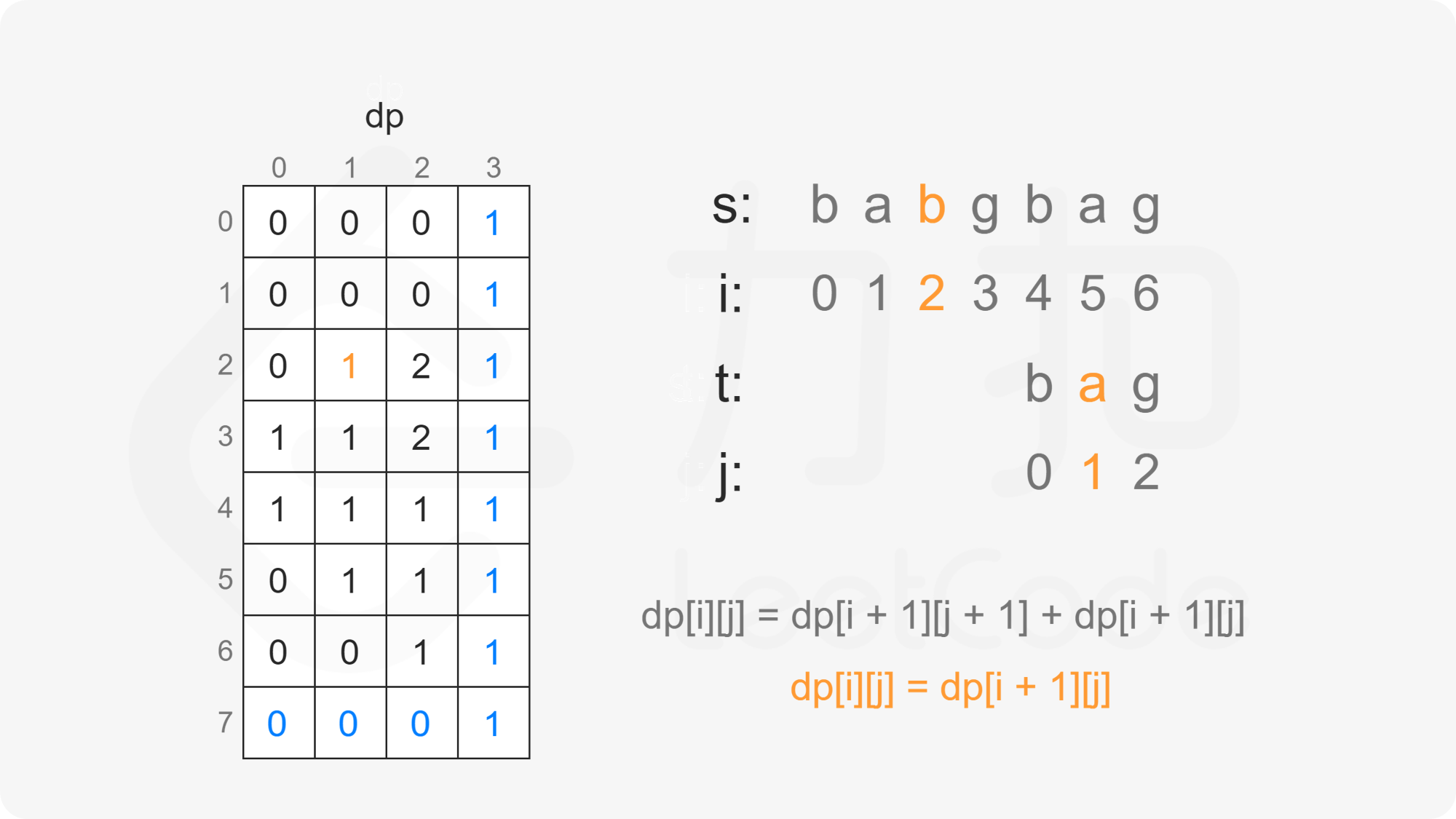
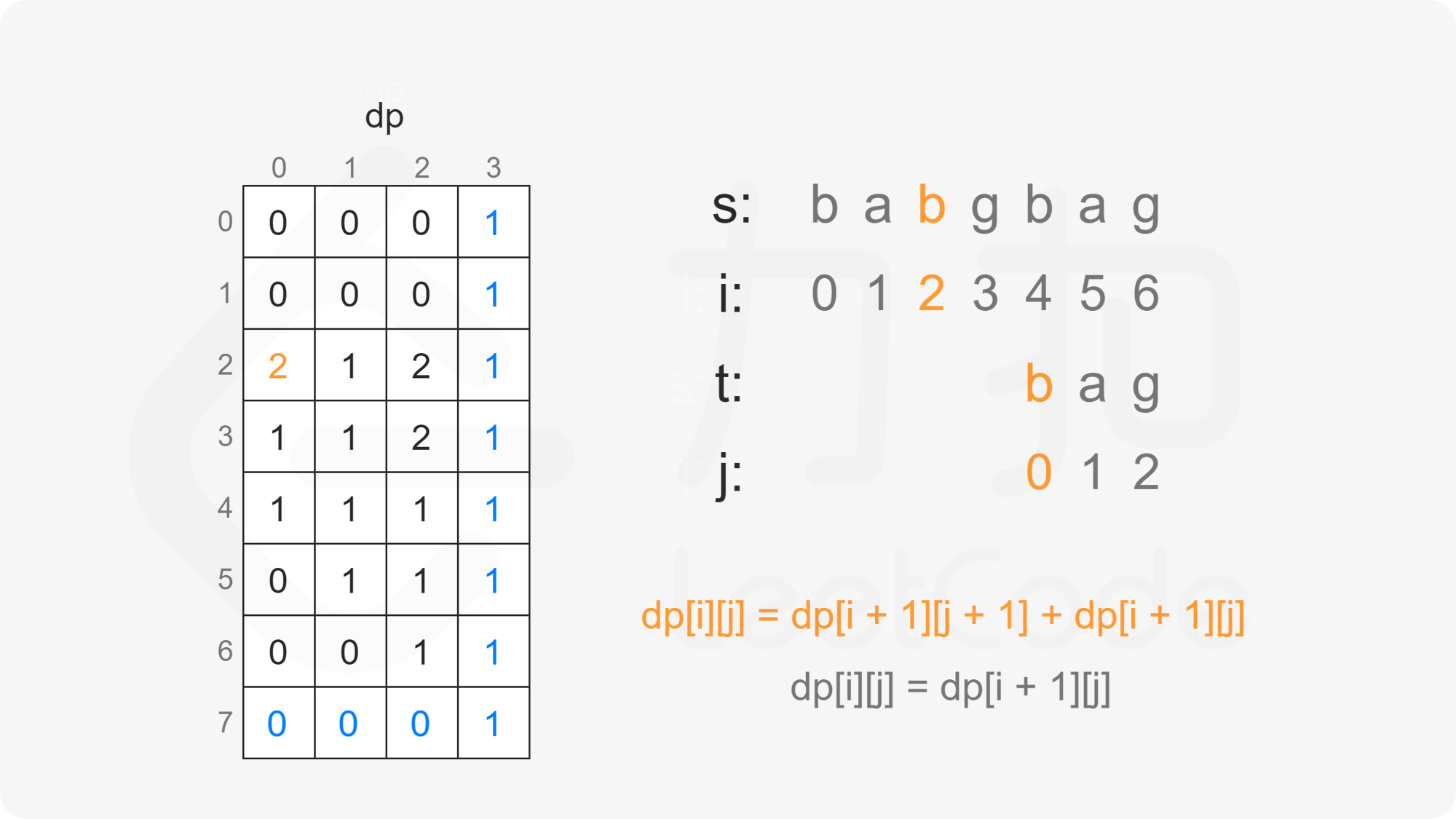
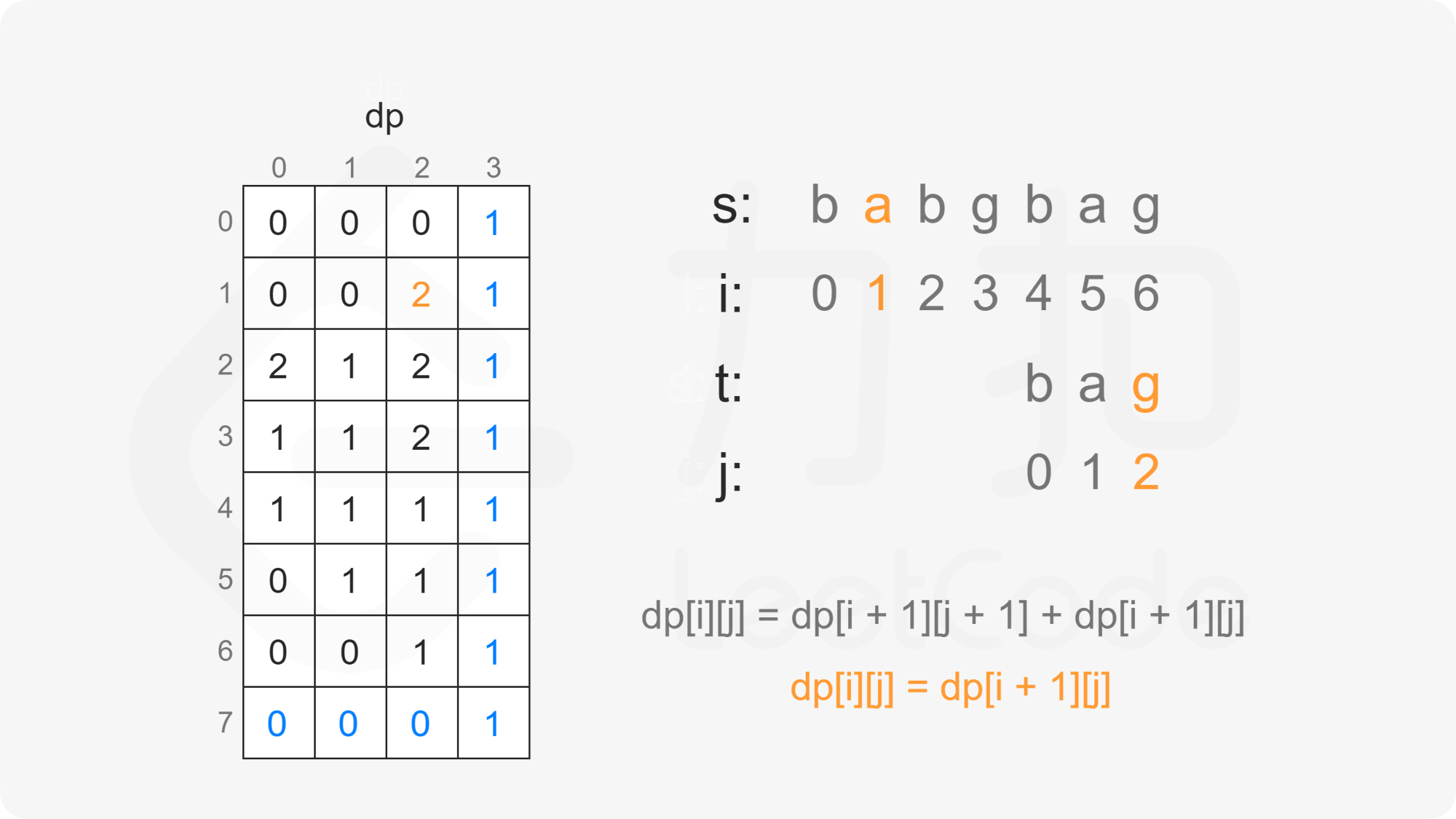
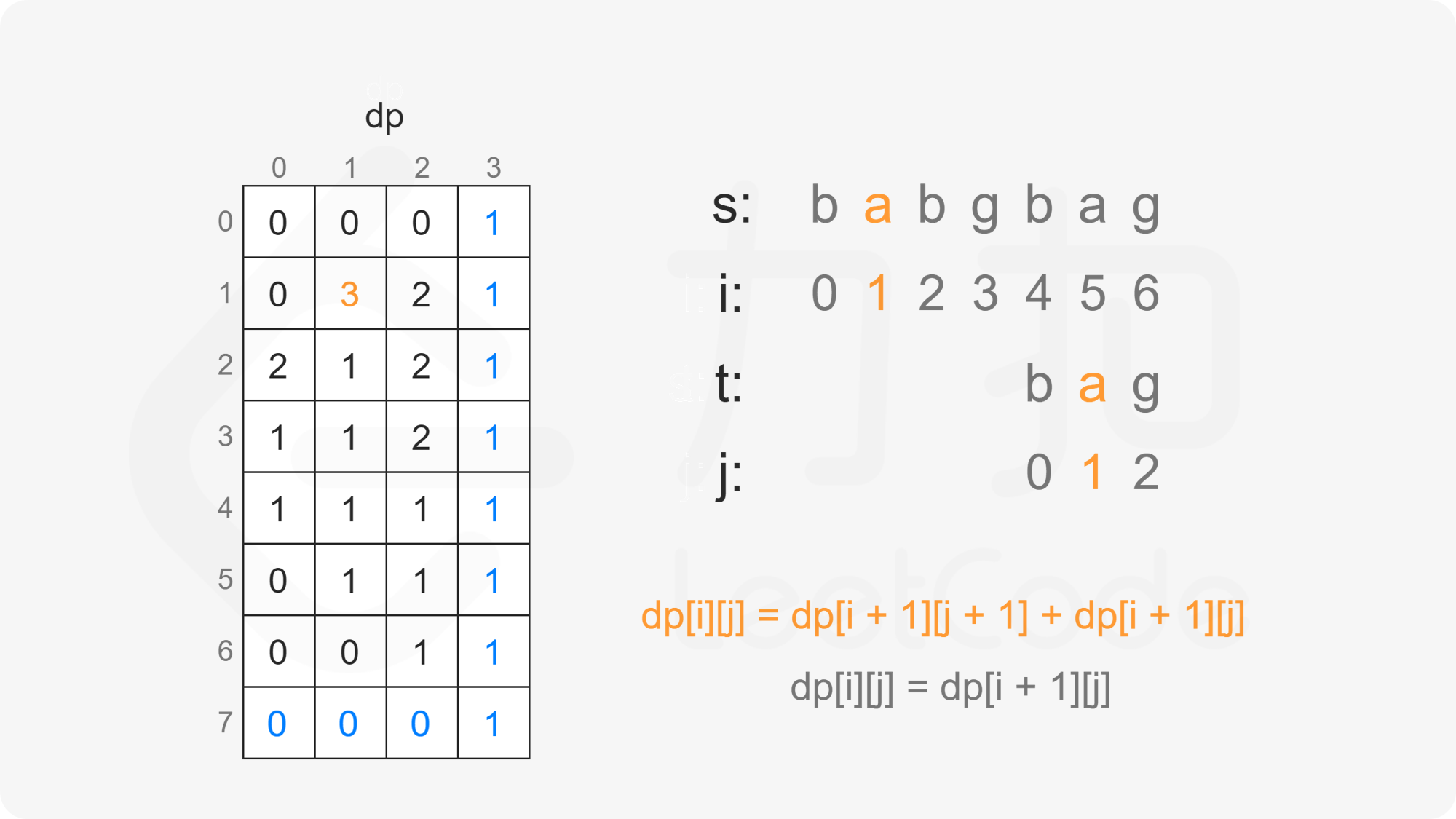
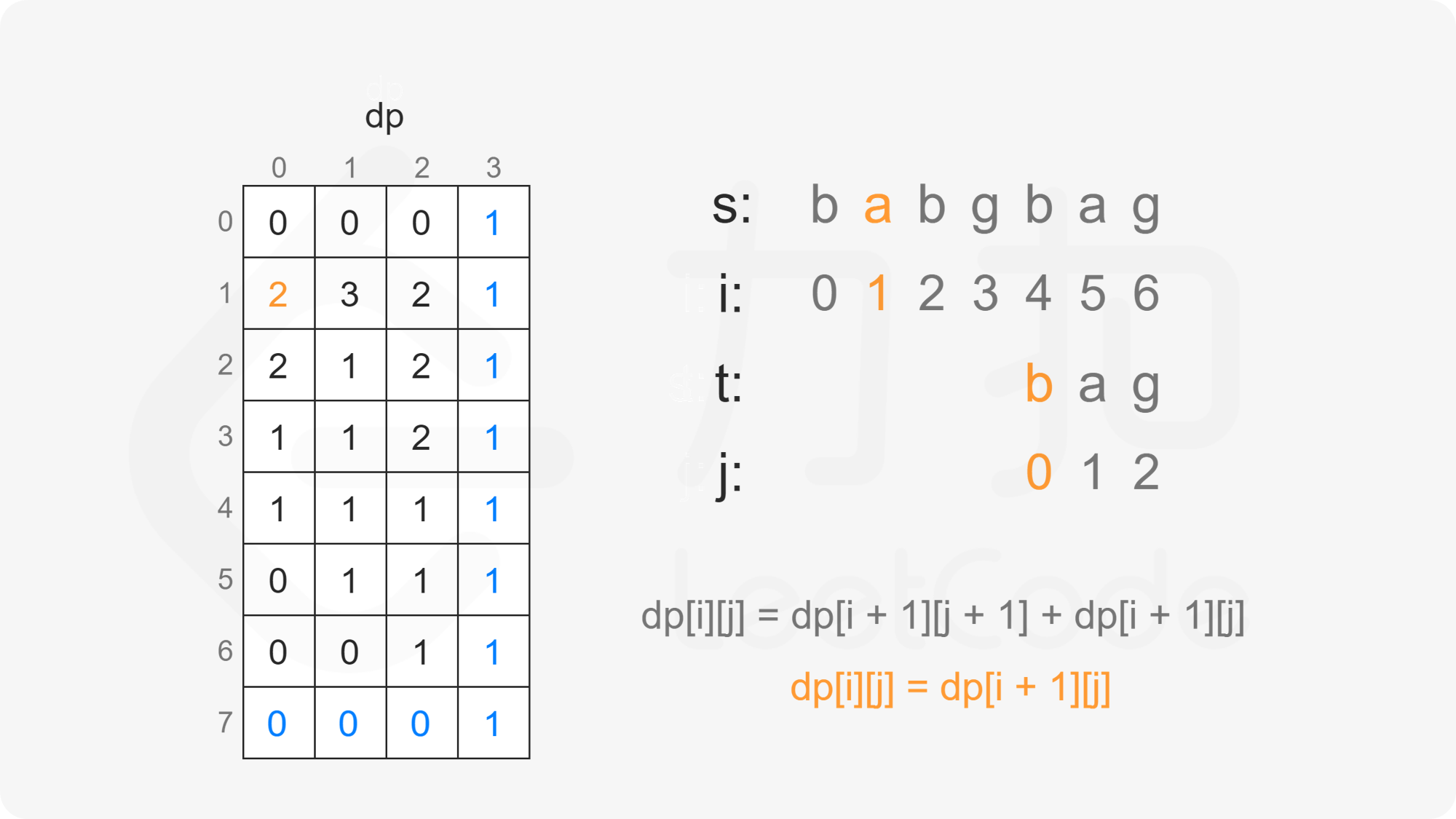
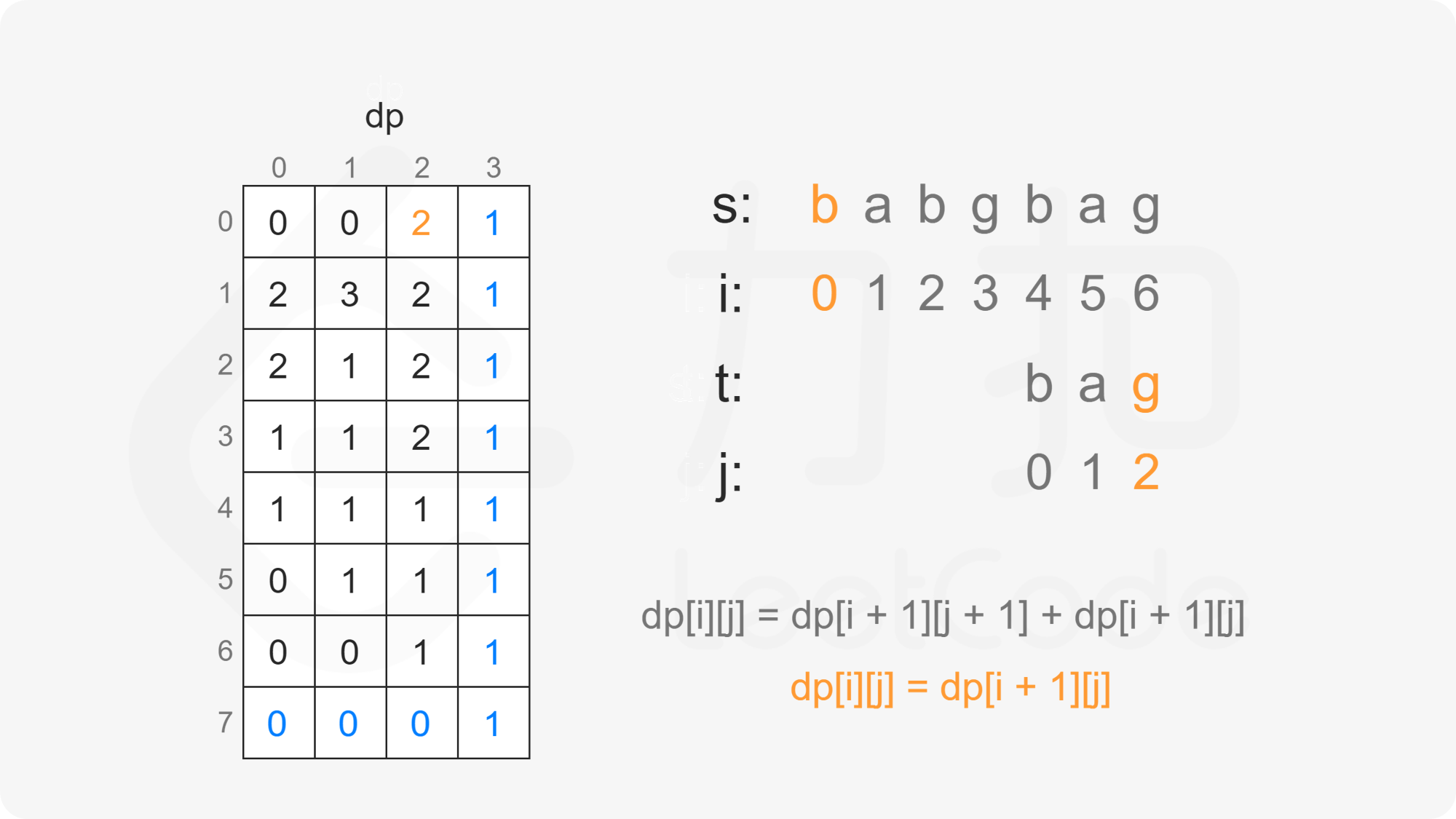
创建二维数组 $\textit{dp}$，其中 $\textit{dp}[i][j]$ 表示在 $s[i:]$ 的子序列中 $t[j:]$ 出现的个数。

上述表示中，$s[i:]$ 表示 $s$ 从下标 $i$ 到末尾的子字符串，$t[j:]$ 表示 $t$ 从下标 $j$ 到末尾的子字符串。

考虑动态规划的边界情况：

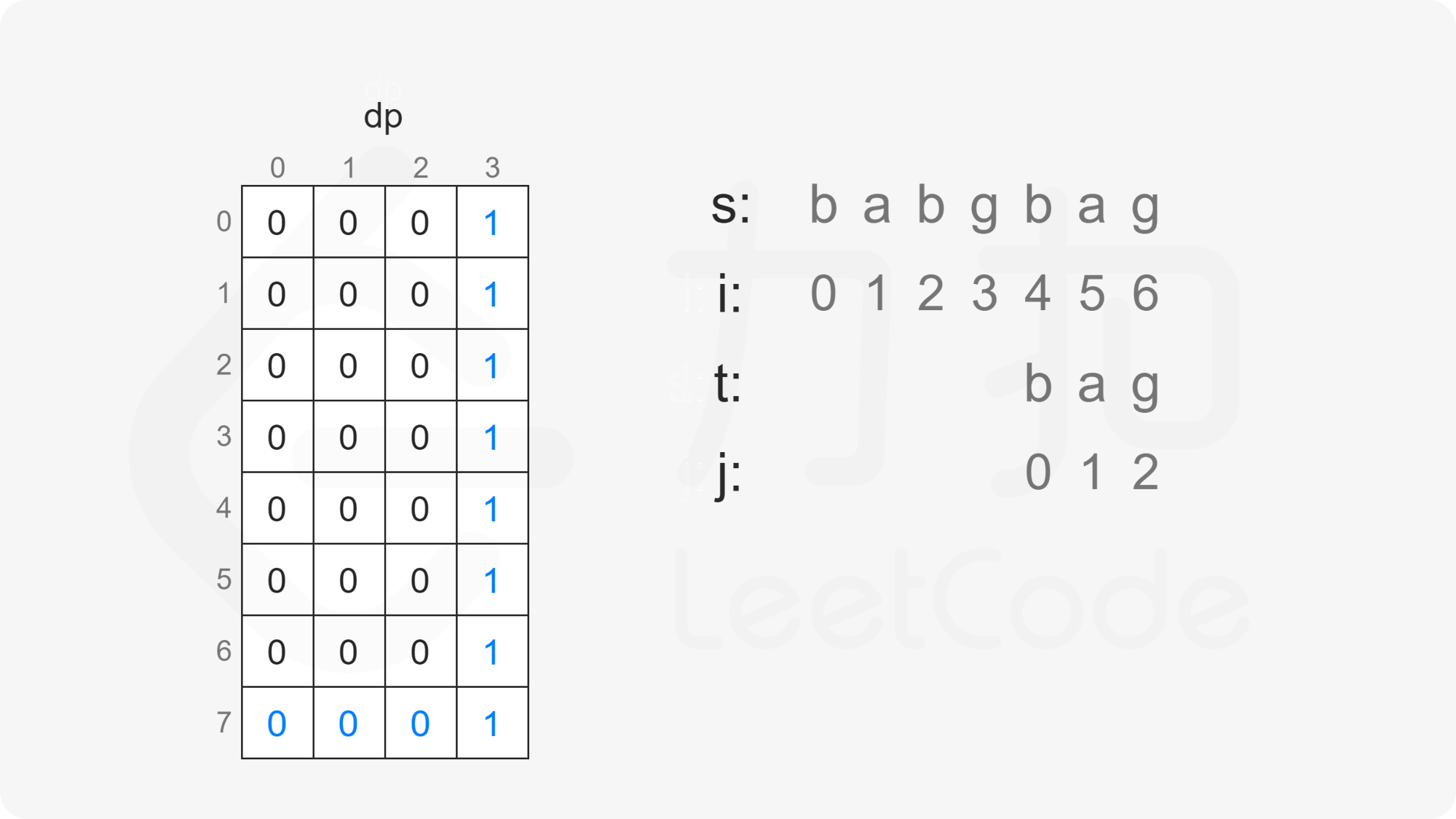
  • 当 $j=n$ 时，$t[j:]$ 为空字符串，由于空字符串是任何字符串的子序列，因此对任意 $0 \le i \le m$，有 $\textit{dp}[i][n]=1$；

  • 当 $i=m$ 且 $j<n$ 时，$s[i:]$ 为空字符串，$t[j:]$ 为非空字符串，由于非空字符串不是空字符串的子序列，因此对任意 $0 \le j<n$，有 $\textit{dp}[m][j]=0$。

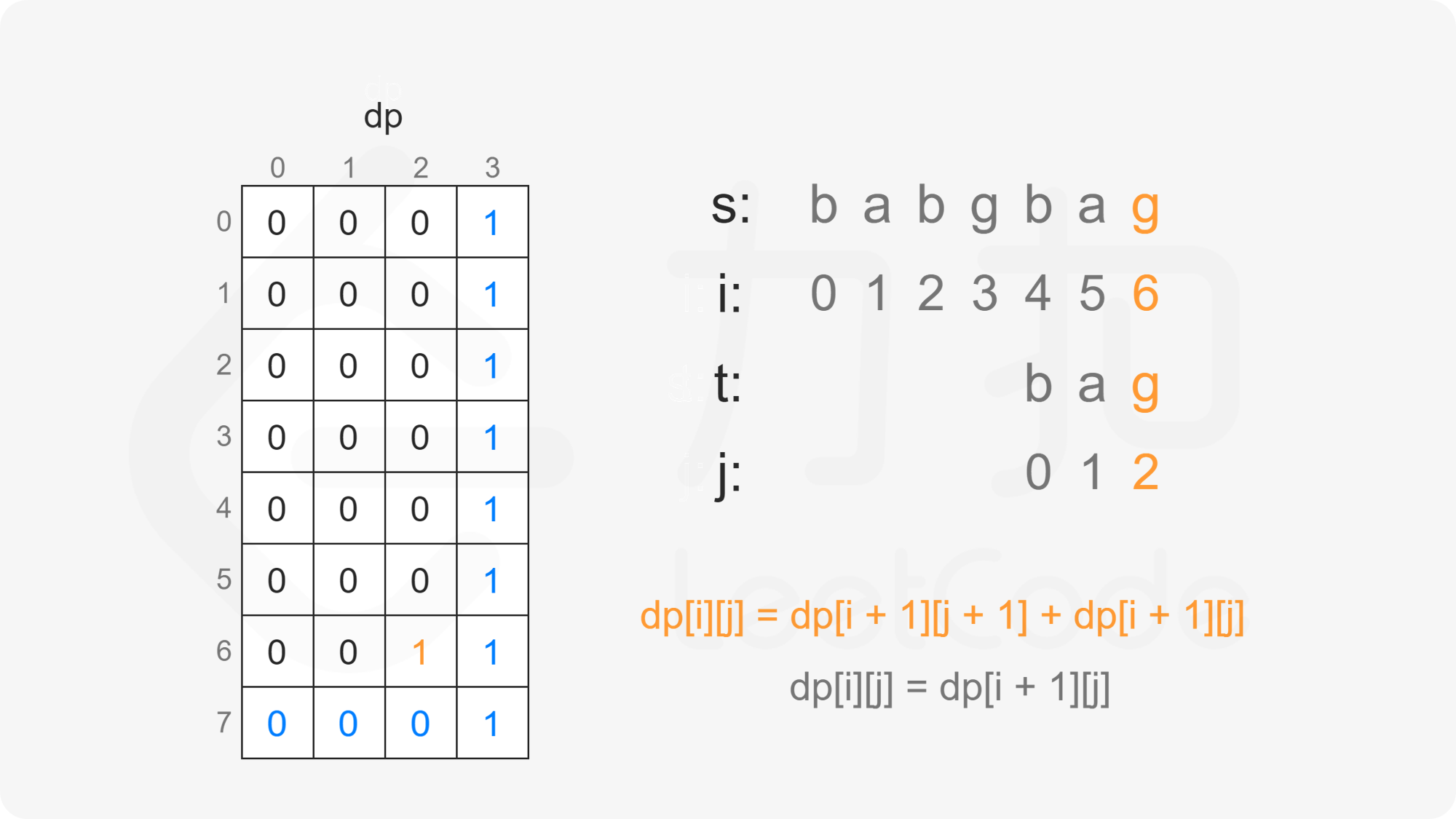
当 $i<m$ 且 $j<n$ 时，考虑 $\textit{dp}[i][j]$ 的计算：

  • 当 $s[i]=t[j]$ 时，$\textit{dp}[i][j]$ 由两部分组成：

    • 如果 $s[i]$ 和 $t[j]$ 匹配，则考虑 $t[j+1:]$ 作为 $s[i+1:]$ 的子序列，子序列数为 $\textit{dp}[i+1][j+1]$；

    • 如果 $s[i]$ 不和 $t[j]$ 匹配，则考虑 $t[j:]$ 作为 $s[i+1:]$ 的子序列，子序列数为 $\textit{dp}[i+1][j]$。

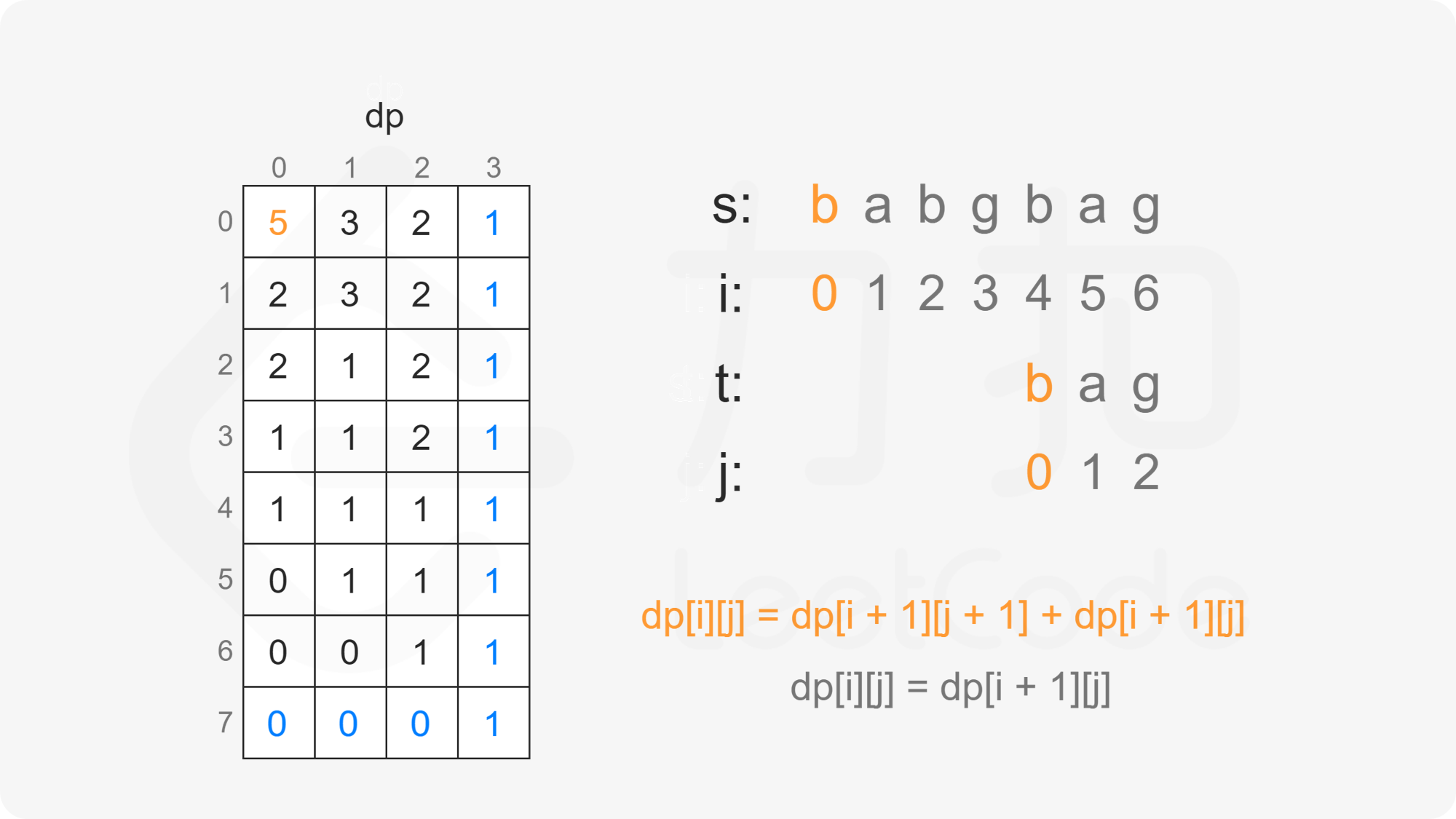
    因此当 $s[i]=t[j]$ 时，有 $\textit{dp}[i][j]=\textit{dp}[i+1][j+1]+\textit{dp}[i+1][j]$。

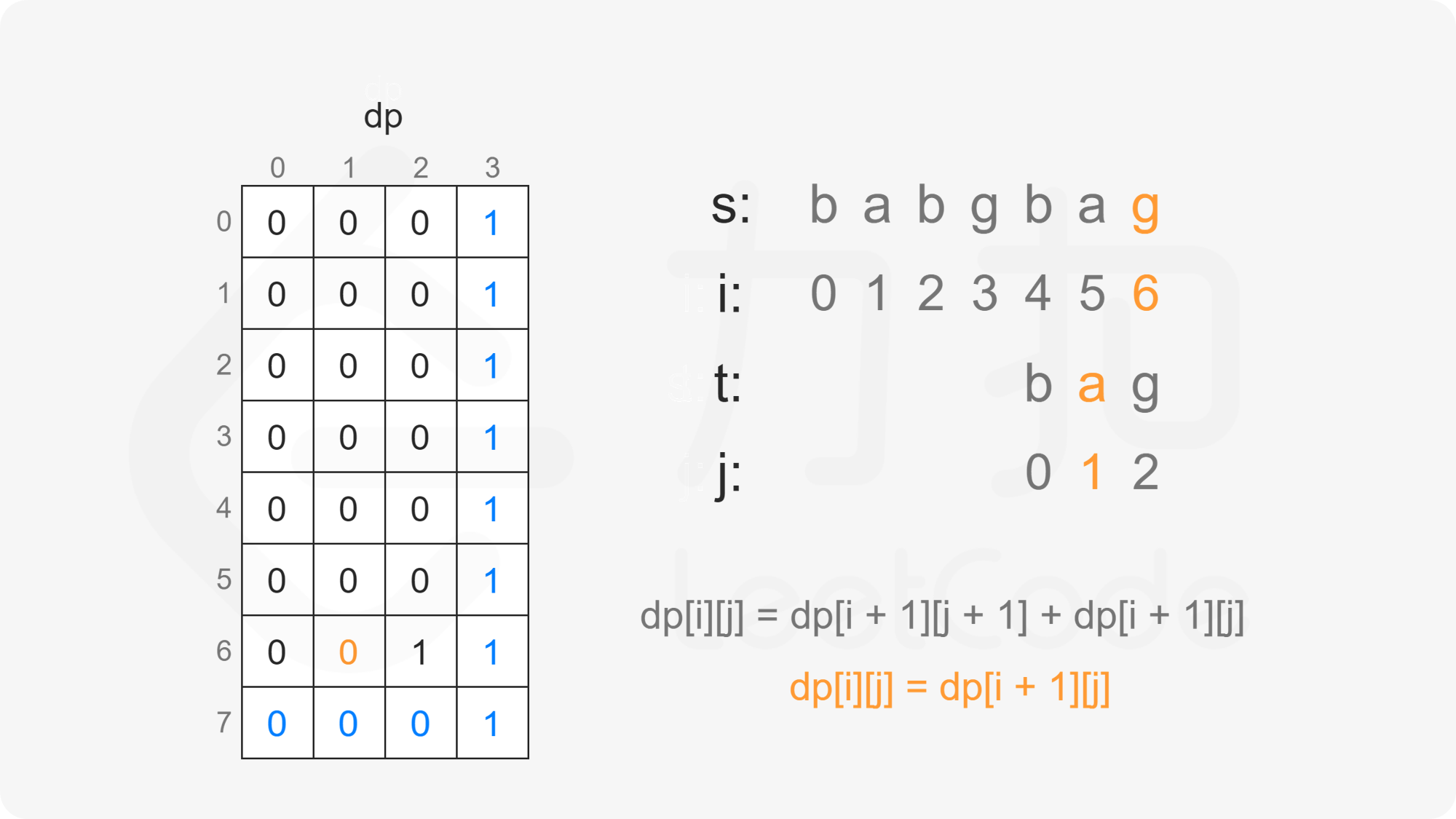
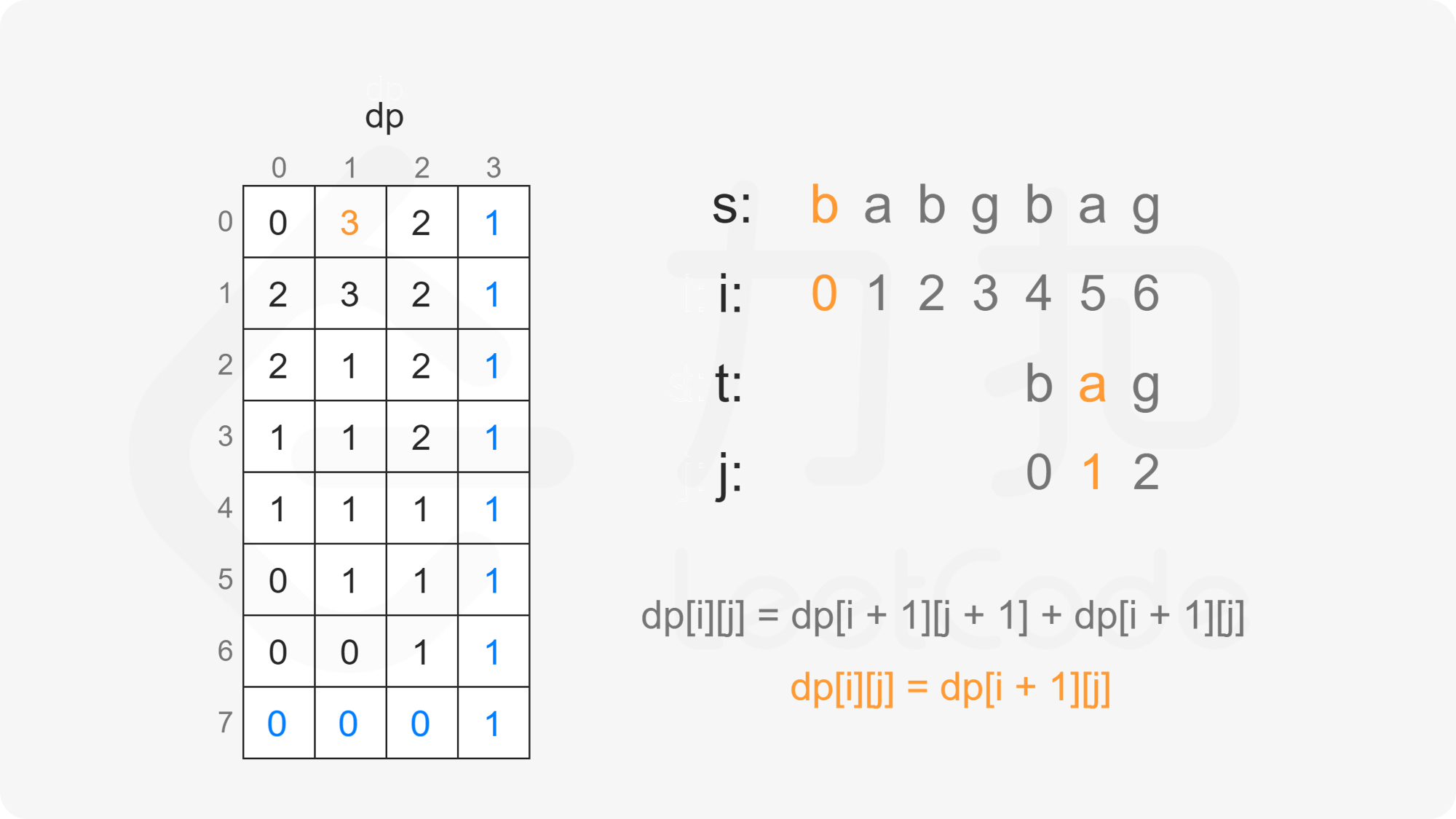
  • 当 $s[i] \ne t[j]$ 时，$s[i]$ 不能和 $t[j]$ 匹配，因此只考虑 $t[j:]$ 作为 $s[i+1:]$ 的子序列，子序列数为 $\textit{dp}[i+1][j]$。

    因此当 $s[i] \ne t[j]$ 时，有 $\textit{dp}[i][j]=\textit{dp}[i+1][j]$。

由此可以得到如下状态转移方程：

$$
\textit{dp}[i][j] = \begin{cases}
\textit{dp}[i+1][j+1]+\textit{dp}[i+1][j], & s[i]=t[j]\
\textit{dp}[i+1][j], & s[i] \ne t[j]
\end{cases}
$$

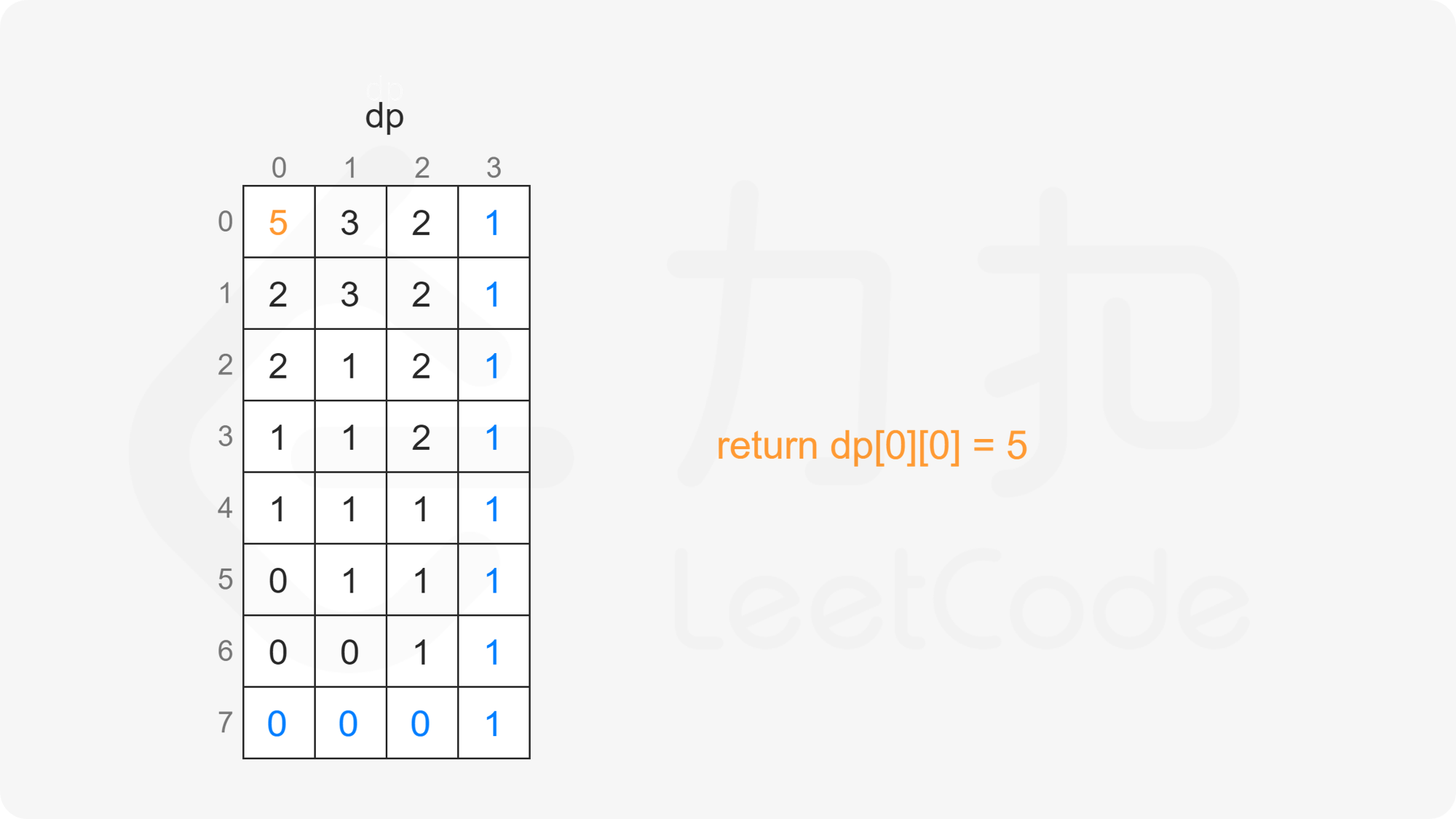
最终计算得到 $\textit{dp}[0][0]$ 即为在 $s$ 的子序列中 $t$ 出现的个数。

<ppt1,ppt2,ppt3,ppt4,ppt5,ppt6,ppt7,ppt8,ppt9,ppt10,ppt11,ppt12,ppt13,ppt14,ppt15,ppt16,ppt17,ppt18,ppt19,ppt20,ppt21,ppt22,ppt23,ppt24>

[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int numDistinct(String s, String t) {
        int m = s.length(), n = t.length();
        if (m < n) {
            return 0;
        }
        int[][] dp = new int[m + 1][n + 1];
        for (int i = 0; i <= m; i++) {
            dp[i][n] = 1;
        }
        for (int i = m - 1; i >= 0; i--) {
            char sChar = s.charAt(i);
            for (int j = n - 1; j >= 0; j--) {
                char tChar = t.charAt(j);
                if (sChar == tChar) {
                    dp[i][j] = dp[i + 1][j + 1] + dp[i + 1][j];
                } else {
                    dp[i][j] = dp[i + 1][j];
                }
            }
        }
        return dp[0][0];
    }
}
[sol1-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
var numDistinct = function(s, t) {
    const m = s.length, n = t.length;
    if (m < n) {
        return 0;
    }
    const dp = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0));
    for (let i = 0; i <= m; i++) {
        dp[i][n] = 1;
    }
    for (let i = m - 1; i >= 0; i--) {
        for (let j = n - 1; j >= 0; j--) {
            if (s[i] == t[j]) {
                dp[i][j] = dp[i + 1][j + 1] + dp[i + 1][j];
            } else {
                dp[i][j] = dp[i + 1][j];
            }
        }
    }
    return dp[0][0];
};
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
func numDistinct(s, t string) int {
    m, n := len(s), len(t)
    if m < n {
        return 0
    }
    dp := make([][]int, m+1)
    for i := range dp {
        dp[i] = make([]int, n+1)
        dp[i][n] = 1
    }
    for i := m - 1; i >= 0; i-- {
        for j := n - 1; j >= 0; j-- {
            if s[i] == t[j] {
                dp[i][j] = dp[i+1][j+1] + dp[i+1][j]
            } else {
                dp[i][j] = dp[i+1][j]
            }
        }
    }
    return dp[0][0]
}
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution:
    def numDistinct(self, s: str, t: str) -> int:
        m, n = len(s), len(t)
        if m < n:
            return 0
        
        dp = [[0] * (n + 1) for _ in range(m + 1)]
        for i in range(m + 1):
            dp[i][n] = 1
        
        for i in range(m - 1, -1, -1):
            for j in range(n - 1, -1, -1):
                if s[i] == t[j]:
                    dp[i][j] = dp[i + 1][j + 1] + dp[i + 1][j]
                else:
                    dp[i][j] = dp[i + 1][j]
        
        return dp[0][0]
[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int numDistinct(string s, string t) {
        int m = s.length(), n = t.length();
        if (m < n) {
            return 0;
        }
        vector<vector<unsigned long long>> dp(m + 1, vector<unsigned long long>(n + 1));
        for (int i = 0; i <= m; i++) {
            dp[i][n] = 1;
        }
        for (int i = m - 1; i >= 0; i--) {
            char sChar = s.at(i);
            for (int j = n - 1; j >= 0; j--) {
                char tChar = t.at(j);
                if (sChar == tChar) {
                    dp[i][j] = dp[i + 1][j + 1] + dp[i + 1][j];
                } else {
                    dp[i][j] = dp[i + 1][j];
                }
            }
        }
        return dp[0][0];
    }
};
[sol1-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int numDistinct(char* s, char* t) {
    int m = strlen(s), n = strlen(t);
    if (m < n) {
        return 0;
    }
    unsigned long long dp[m + 1][n + 1];
    memset(dp, 0, sizeof(dp));
    for (int i = 0; i <= m; i++) {
        dp[i][n] = 1;
    }
    for (int i = m - 1; i >= 0; i--) {
        char sChar = s[i];
        for (int j = n - 1; j >= 0; j--) {
            char tChar = t[j];
            if (sChar == tChar) {
                dp[i][j] = dp[i + 1][j + 1] + dp[i + 1][j];
            } else {
                dp[i][j] = dp[i + 1][j];
            }
        }
    }
    return dp[0][0];
}

复杂度分析

  • 时间复杂度：$O(mn)$，其中 $m$ 和 $n$ 分别是字符串 $s$ 和 $t$ 的长度。二维数组 $\textit{dp}$ 有 $m+1$ 行和 $n+1$ 列，需要对 $\textit{dp}$ 中的每个元素进行计算。

  • 空间复杂度：$O(mn)$，其中 $m$ 和 $n$ 分别是字符串 $s$ 和 $t$ 的长度。创建了 $m+1$ 行 $n+1$ 列的二维数组 $\textit{dp}$。

 Comments
On this page
0115-不同的子序列