0221-最大正方形

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 10:44:06 2023-09-13 10:44:06 Updated    

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

示例 1：

**输入：** matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
**输出：** 4

示例 2：

**输入：** matrix = [["0","1"],["1","0"]]
**输出：** 1

示例 3：

**输入：** matrix = [["0"]]
**输出：** 0

提示：

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 300
  • matrix[i][j] 为 '0' 或 '1'

📺 视频题解

221. 最大正方形.mp4

📖 文字题解

方法一：暴力法

由于正方形的面积等于边长的平方，因此要找到最大正方形的面积，首先需要找到最大正方形的边长，然后计算最大边长的平方即可。

暴力法是最简单直观的做法，具体做法如下：

  • 遍历矩阵中的每个元素，每次遇到 $1$，则将该元素作为正方形的左上角；

  • 确定正方形的左上角后，根据左上角所在的行和列计算可能的最大正方形的边长（正方形的范围不能超出矩阵的行数和列数），在该边长范围内寻找只包含 $1$ 的最大正方形；

  • 每次在下方新增一行以及在右方新增一列，判断新增的行和列是否满足所有元素都是 $1$。

[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
    public int maximalSquare(char[][] matrix) {
        int maxSide = 0;
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return maxSide;
        }
        int rows = matrix.length, columns = matrix[0].length;
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < columns; j++) {
                if (matrix[i][j] == '1') {
                    // 遇到一个 1 作为正方形的左上角
                    maxSide = Math.max(maxSide, 1);
                    // 计算可能的最大正方形边长
                    int currentMaxSide = Math.min(rows - i, columns - j);
                    for (int k = 1; k < currentMaxSide; k++) {
                        // 判断新增的一行一列是否均为 1
                        boolean flag = true;
                        if (matrix[i + k][j + k] == '0') {
                            break;
                        }
                        for (int m = 0; m < k; m++) {
                            if (matrix[i + k][j + m] == '0' || matrix[i + m][j + k] == '0') {
                                flag = false;
                                break;
                            }
                        }
                        if (flag) {
                            maxSide = Math.max(maxSide, k + 1);
                        } else {
                            break;
                        }
                    }
                }
            }
        }
        int maxSquare = maxSide * maxSide;
        return maxSquare;
    }
}
[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        if (matrix.size() == 0 || matrix[0].size() == 0) {
            return 0;
        }
        int maxSide = 0;
        int rows = matrix.size(), columns = matrix[0].size();
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < columns; j++) {
                if (matrix[i][j] == '1') {
                    // 遇到一个 1 作为正方形的左上角
                    maxSide = max(maxSide, 1);
                    // 计算可能的最大正方形边长
                    int currentMaxSide = min(rows - i, columns - j);
                    for (int k = 1; k < currentMaxSide; k++) {
                        // 判断新增的一行一列是否均为 1
                        bool flag = true;
                        if (matrix[i + k][j + k] == '0') {
                            break;
                        }
                        for (int m = 0; m < k; m++) {
                            if (matrix[i + k][j + m] == '0' || matrix[i + m][j + k] == '0') {
                                flag = false;
                                break;
                            }
                        }
                        if (flag) {
                            maxSide = max(maxSide, k + 1);
                        } else {
                            break;
                        }
                    }
                }
            }
        }
        int maxSquare = maxSide * maxSide;
        return maxSquare;
    }
};
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution:
    def maximalSquare(self, matrix: List[List[str]]) -> int:
        if len(matrix) == 0 or len(matrix[0]) == 0:
            return 0
        
        maxSide = 0
        rows, columns = len(matrix), len(matrix[0])
        for i in range(rows):
            for j in range(columns):
                if matrix[i][j] == '1':
                    # 遇到一个 1 作为正方形的左上角
                    maxSide = max(maxSide, 1)
                    # 计算可能的最大正方形边长
                    currentMaxSide = min(rows - i, columns - j)
                    for k in range(1, currentMaxSide):
                        # 判断新增的一行一列是否均为 1
                        flag = True
                        if matrix[i + k][j + k] == '0':
                            break
                        for m in range(k):
                            if matrix[i + k][j + m] == '0' or matrix[i + m][j + k] == '0':
                                flag = False
                                break
                        if flag:
                            maxSide = max(maxSide, k + 1)
                        else:
                            break
        
        maxSquare = maxSide * maxSide
        return maxSquare
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
func maximalSquare(matrix [][]byte) int {
    maxSide := 0
    if len(matrix) == 0 || len(matrix[0]) == 0 {
        return maxSide
    }
    rows, columns := len(matrix), len(matrix[0])
    for i := 0; i < rows; i++ {
        for j := 0; j < columns; j++ {
            if matrix[i][j] == '1' {
                maxSide = max(maxSide, 1)
                curMaxSide := min(rows - i, columns - j)
                for k := 1; k < curMaxSide; k++ {
                    flag := true
                    if matrix[i+k][j+k] == '0' {
                        break
                    }
                    for m := 0; m < k; m++ {
                        if matrix[i+k][j+m] == '0' || matrix[i+m][j+k] == '0' {
                            flag = false
                            break
                        }
                    }
                    if flag {
                        maxSide = max(maxSide, k + 1)
                    } else {
                        break
                    }
                }
            }
        }
    }
    return maxSide * maxSide
}

func max(x, y int) int {
    if x > y {
        return x
    }
    return y
}

func min(x, y int) int {
    if x < y {
        return x
    }
    return y
}

复杂度分析

  • 时间复杂度：$O(mn \min(m,n)^2)$，其中 $m$ 和 $n$ 是矩阵的行数和列数。

    • 需要遍历整个矩阵寻找每个 $1$，遍历矩阵的时间复杂度是 $O(mn)$。
    • 对于每个可能的正方形，其边长不超过 $m$ 和 $n$ 中的最小值，需要遍历该正方形中的每个元素判断是不是只包含 $1$，遍历正方形时间复杂度是 $O(\min(m,n)^2)$。
    • 总时间复杂度是 $O(mn \min(m,n)^2)$。

  • 空间复杂度：$O(1)$。额外使用的空间复杂度为常数。

方法二：动态规划

方法一虽然直观，但是时间复杂度太高，有没有办法降低时间复杂度呢？

可以使用动态规划降低时间复杂度。我们用 $\textit{dp}(i, j)$ 表示以 $(i, j)$ 为右下角，且只包含 $1$ 的正方形的边长最大值。如果我们能计算出所有 $\textit{dp}(i, j)$ 的值，那么其中的最大值即为矩阵中只包含 $1$ 的正方形的边长最大值，其平方即为最大正方形的面积。

那么如何计算 $\textit{dp}$ 中的每个元素值呢？对于每个位置 $(i, j)$，检查在矩阵中该位置的值：

  • 如果该位置的值是 $0$，则 $\textit{dp}(i, j) = 0$，因为当前位置不可能在由 $1$ 组成的正方形中；

  • 如果该位置的值是 $1$，则 $\textit{dp}(i, j)$ 的值由其上方、左方和左上方的三个相邻位置的 $\textit{dp}$ 值决定。具体而言，当前位置的元素值等于三个相邻位置的元素中的最小值加 $1$，状态转移方程如下：

    $$
    dp(i, j)=min(dp(i−1, j), dp(i−1, j−1), dp(i, j−1))+1
    $$

    如果读者对这个状态转移方程感到不解，可以参考 1277. 统计全为 1 的正方形子矩阵的官方题解 ，其中给出了详细的证明。

    此外，还需要考虑边界条件。如果 $i$ 和 $j$ 中至少有一个为 $0$，则以位置 $(i, j)$ 为右下角的最大正方形的边长只能是 $1$，因此 $\textit{dp}(i, j) = 1$。

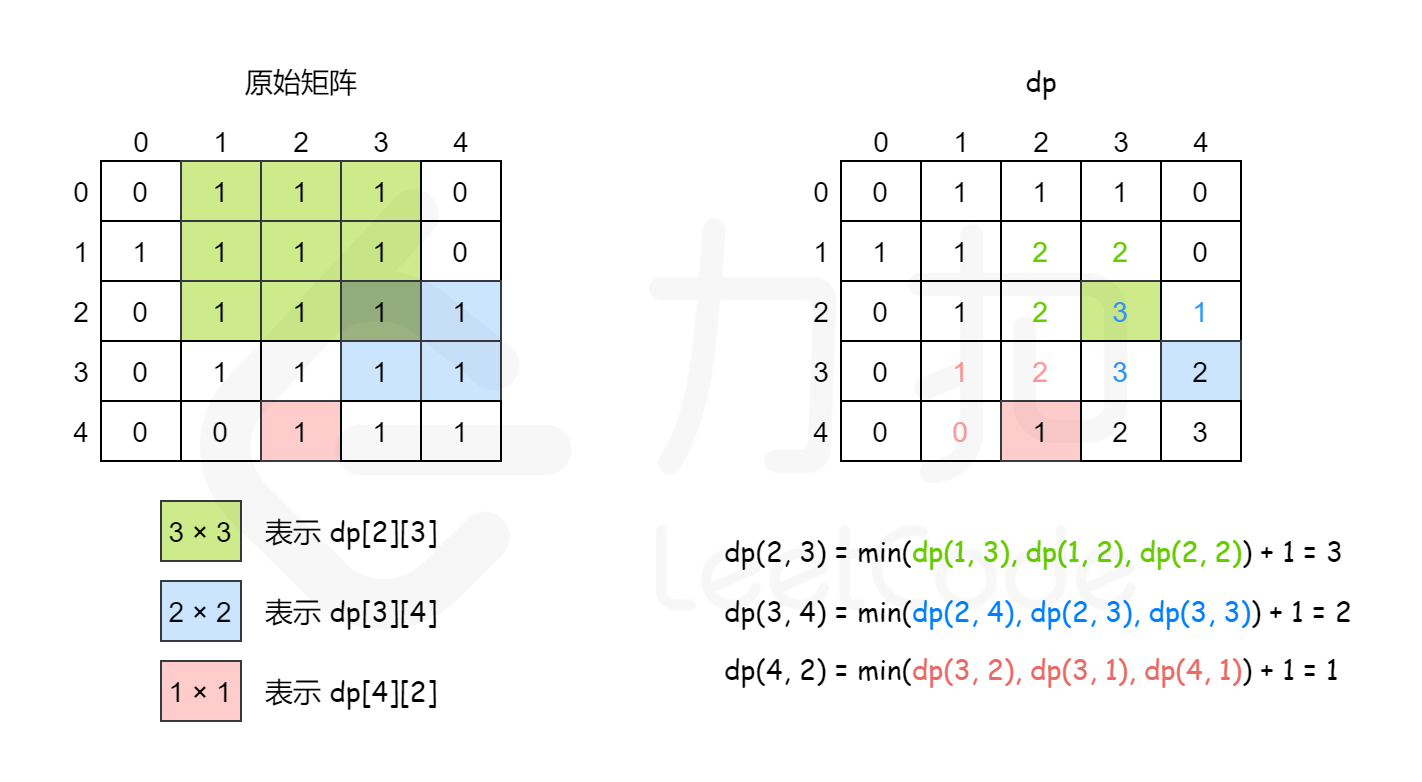
以下用一个例子具体说明。原始矩阵如下。

1
2
3
4
5
0 1 1 1 0
1 1 1 1 0
0 1 1 1 1
0 1 1 1 1
0 0 1 1 1

对应的 $\textit{dp}$ 值如下。

1
2
3
4
5
0 1 1 1 0
1 1 2 2 0
0 1 2 3 1
0 1 2 3 2
0 0 1 2 3

下图也给出了计算 $\textit{dp}$ 值的过程。

fig1

[sol2-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int maximalSquare(char[][] matrix) {
        int maxSide = 0;
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return maxSide;
        }
        int rows = matrix.length, columns = matrix[0].length;
        int[][] dp = new int[rows][columns];
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < columns; j++) {
                if (matrix[i][j] == '1') {
                    if (i == 0 || j == 0) {
                        dp[i][j] = 1;
                    } else {
                        dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
                    }
                    maxSide = Math.max(maxSide, dp[i][j]);
                }
            }
        }
        int maxSquare = maxSide * maxSide;
        return maxSquare;
    }
}
[sol2-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        if (matrix.size() == 0 || matrix[0].size() == 0) {
            return 0;
        }
        int maxSide = 0;
        int rows = matrix.size(), columns = matrix[0].size();
        vector<vector<int>> dp(rows, vector<int>(columns));
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < columns; j++) {
                if (matrix[i][j] == '1') {
                    if (i == 0 || j == 0) {
                        dp[i][j] = 1;
                    } else {
                        dp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
                    }
                    maxSide = max(maxSide, dp[i][j]);
                }
            }
        }
        int maxSquare = maxSide * maxSide;
        return maxSquare;
    }
};
[sol2-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution:
    def maximalSquare(self, matrix: List[List[str]]) -> int:
        if len(matrix) == 0 or len(matrix[0]) == 0:
            return 0
        
        maxSide = 0
        rows, columns = len(matrix), len(matrix[0])
        dp = [[0] * columns for _ in range(rows)]
        for i in range(rows):
            for j in range(columns):
                if matrix[i][j] == '1':
                    if i == 0 or j == 0:
                        dp[i][j] = 1
                    else:
                        dp[i][j] = min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]) + 1
                    maxSide = max(maxSide, dp[i][j])
        
        maxSquare = maxSide * maxSide
        return maxSquare
[sol2-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
func maximalSquare(matrix [][]byte) int {
    dp := make([][]int, len(matrix))
    maxSide := 0
    for i := 0; i < len(matrix); i++ {
        dp[i] = make([]int, len(matrix[i]))
        for j := 0; j < len(matrix[i]); j++ {
            dp[i][j] = int(matrix[i][j] - '0')
            if dp[i][j] == 1 {
                maxSide = 1
            }
        }
    }

    for i := 1; i < len(matrix); i++ {
        for j := 1; j < len(matrix[i]); j++ {
            if dp[i][j] == 1 {
                dp[i][j] = min(min(dp[i-1][j], dp[i][j-1]), dp[i-1][j-1]) + 1
                if dp[i][j] > maxSide {
                    maxSide = dp[i][j]
                }
            }
        }
    }
    return maxSide * maxSide
}

func min(x, y int) int {
    if x < y {
        return x
    }
    return y
}

复杂度分析

  • 时间复杂度：$O(mn)$，其中 $m$ 和 $n$ 是矩阵的行数和列数。需要遍历原始矩阵中的每个元素计算 $\textit{dp}$ 的值。

  • 空间复杂度：$O(mn)$，其中 $m$ 和 $n$ 是矩阵的行数和列数。创建了一个和原始矩阵大小相同的矩阵 $\textit{dp}$。由于状态转移方程中的 $\textit{dp}(i, j)$ 由其上方、左方和左上方的三个相邻位置的 $\textit{dp}$ 值决定，因此可以使用两个一维数组进行状态转移，空间复杂度优化至 $O(n)$。

 Comments
On this page
0221-最大正方形
  1. 📺 视频题解
  2. 📖 文字题解