0287-寻找重复数

给定一个包含 n + 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。

假设 nums 只有 一个重复的整数 ，返回 这个重复的数 。

你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。

示例 1：

**输入：** nums = [1,3,4,2,2]
**输出：** 2

示例 2：

**输入：** nums = [3,1,3,4,2]
**输出：** 3

提示：

• 1 <= n <= 105
• nums.length == n + 1
• 1 <= nums[i] <= n
• nums 中 只有一个整数 出现 两次或多次 ，其余整数均只出现 一次

进阶：

• 如何证明 nums 中至少存在一个重复的数字?
• 你可以设计一个线性级时间复杂度 O(n) 的解决方案吗？

📺 视频题解

📖 文字题解

方法一：二分查找

思路和算法

我们定义 cnt}[i]$ 表示 nums 数组中小于等于 $i$ 的数有多少个，假设我们重复的数是 target，那么 $[1,\textit{target}-1]$里的所有数满足 cnt}[i]\le i$，$[target,n]$ 里的所有数满足 cnt}[i]>i$，具有单调性。

以示例 1 为例，我们列出每个数字的 cnt 值：

nums	1	2	3	4
cnt	1	3	4	5

示例中重复的整数是 $2$，我们可以看到 $[1,1]$ 中的数满足 cnt}[i]\le i$，$[2,4]$ 中的数满足 cnt}[i]>i$ 。

如果知道 cnt}[]$ 数组随数字 $i$ 逐渐增大具有单调性（即 target 前 cnt}[i]\le i$，target 后 cnt}[i]>i$），那么我们就可以直接利用二分查找来找到重复的数。

但这个性质一定是正确的吗？考虑 nums 数组一共有 $n+1$ 个位置，我们填入的数字都在 $[1,n]$ 间，有且只有一个数重复放了两次以上。对于所有测试用例，考虑以下两种情况：

• 如果测试用例的数组中 target 出现了两次，其余的数各出现了一次，这个时候肯定满足上文提及的性质，因为小于 target 的数 $i$ 满足 cnt}[i]=i$，大于等于 target 的数 $j$ 满足 $cnt[j]=j+1$。

• 如果测试用例的数组中 target 出现了三次及以上，那么必然有一些数不在 nums 数组中了，这个时候相当于我们用 target 去替换了这些数，我们考虑替换的时候对 cnt}[]$ 数组的影响。如果替换的数 $i$ 小于 target ，那么 $[i, \textit{target}-1]$ 的 cnt 值均减一，其他不变，满足条件。如果替换的数 $j$ 大于等于 target，那么 $[\textit{target}, j-1]$ 的 cnt 值均加一，其他不变，亦满足条件。

因此我们生成的数组一定具有上述性质的。

[sol1-C++]

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int n = nums.size();
        int l = 1, r = n - 1, ans = -1;
        while (l <= r) {
            int mid = (l + r) >> 1;
            int cnt = 0;
            for (int i = 0; i < n; ++i) {
                cnt += nums[i] <= mid;
            }
            if (cnt <= mid) {
                l = mid + 1;
            } else {
                r = mid - 1;
                ans = mid;
            }
        }
        return ans;
    }
};

[sol1-JavaScript]

var findDuplicate = function(nums) {
    const n = nums.length;
    let l = 1, r = n - 1, ans = -1;
    while (l <= r) {
        let mid = (l + r) >> 1;
        let cnt = 0;
        for (let i = 0; i < n; ++i) {
            cnt += nums[i] <= mid;
        }
        if (cnt <= mid) {
            l = mid + 1;
        } else {
            r = mid - 1;
            ans = mid;
        }
    }
    return ans;
};

[sol1-Java]

class Solution {
    public int findDuplicate(int[] nums) {
        int n = nums.length;
        int l = 1, r = n - 1, ans = -1;
        while (l <= r) {
            int mid = (l + r) >> 1;
            int cnt = 0;
            for (int i = 0; i < n; ++i) {
                if (nums[i] <= mid) {
                    cnt++;
                }
            }
            if (cnt <= mid) {
                l = mid + 1;
            } else {
                r = mid - 1;
                ans = mid;
            }
        }
        return ans;
    }
}

[sol1-Golang]

func findDuplicate(nums []int) int {
    n := len(nums)
    l, r := 1, n - 1
    ans := -1
    for l <= r {
        mid := (l + r) >> 1
        cnt := 0
        for i := 0; i < n; i++ {
            if nums[i] <= mid {
                cnt++
            }
        }
        if cnt <= mid {
            l = mid + 1
        } else {
            r = mid - 1
            ans = mid
        }
    }
    return ans
}

复杂度分析

• 时间复杂度：$O(n\log n)$，其中 $n$ 为 nums 数组的长度。二分查找最多需要二分 $O(\log n)$ 次，每次判断的时候需要$O(n)$ 遍历 nums 数组求解小于等于 mid 的数的个数，因此总时间复杂度为 $O(n\log n)$。
• 空间复杂度：$O(1)$。我们只需要常数空间存放若干变量。

方法二：二进制

思路和算法

这个方法我们来将所有数二进制展开按位考虑如何找出重复的数，如果我们能确定重复数每一位是 $1$ 还是 $0$ 就可以按位还原出重复的数是什么。

考虑到第 $i$ 位，我们记 nums 数组中二进制展开后第 $i$ 位为 $1$ 的数有 $x$ 个，数字 $[1,n]$ 这 $n$ 个数二进制展开后第 $i$ 位为 $1$ 的数有 $y$ 个，那么重复的数第 $i$ 位为 $1$ 当且仅当 $x>y$。

仍然以示例 1 为例，如下的表格列出了每个数字二进制下每一位是 $1$ 还是 $0$ 以及对应位的 $x$ 和 $y$ 是多少：

	1	3	4	2	2	x	y
第 0 位	1	1	0	0	0	2	2
第 1 位	0	1	0	1	1	3	2
第 2 位	0	0	1	0	0	1	1

那么按之前说的我们发现只有第 $1$ 位 $x>y$ ，所以按位还原后 target}=(010)2=(2){10，符合答案。

正确性的证明其实和方法一类似，我们可以按方法一的方法，考虑不同示例数组中第 $i$ 位 $1$ 的个数 $x$ 的变化：

• 如果测试用例的数组中 target 出现了两次，其余的数各出现了一次，且 target 的第 $i$ 位为 $1$，那么 nums 数组中第 $i$ 位 $1$ 的个数 $x$ 恰好比 $y$ 大一。如果target 的第 $i$ 位为 $0$，那么两者相等。
• 如果测试用例的数组中 target 出现了三次及以上，那么必然有一些数不在 nums 数组中了，这个时候相当于我们用 target 去替换了这些数，我们考虑替换的时候对 $x$ 的影响：
  • 如果被替换的数第 $i$ 位为 $1$，且 target 第 $i$ 位为 $1$：$x$ 不变，满足 $x>y$。
  • 如果被替换的数第 $i$ 位为 $0$，且 target 第 $i$ 位为 $1$：$x$ 加一，满足 $x>y$。
  • 如果被替换的数第 $i$ 位为 $1$，且 target 第 $i$ 位为 $0$：$x$ 减一，满足 $x\le y$。
  • 如果被替换的数第 $i$ 位为 $0$，且 target 第 $i$ 位为 $0$：$x$ 不变，满足 $x\le y$。

也就是说如果 target 第 $i$ 位为 $1$，那么每次替换后只会使 $x$ 不变或增大，如果为 $0$，只会使 $x$ 不变或减小，始终满足 $x>y$ 时 target 第 $i$ 位为 $1$，否则为 $0$，因此我们只要按位还原这个重复的数即可。

[sol2-C++]

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int n = nums.size(), ans = 0;
        // 确定二进制下最高位是多少
        int bit_max = 31;
        while (!((n - 1) >> bit_max)) {
            bit_max -= 1;
        }
        for (int bit = 0; bit <= bit_max; ++bit) {
            int x = 0, y = 0;
            for (int i = 0; i < n; ++i) {
                if (nums[i] & (1 << bit)) {
                    x += 1;
                }
                if (i >= 1 && (i & (1 << bit))) {
                    y += 1;
                }
            }
            if (x > y) {
                ans |= 1 << bit;
            }
        }
        return ans;
    }
};

[sol2-JavaScript]

var findDuplicate = function(nums) {
    const n = nums.length;
    let ans = 0;
    // 确定二进制下最高位是多少
    let bit_max = 31;
    while (!((n - 1) >> bit_max)) {
        bit_max -= 1;
    }
    for (let bit = 0; bit <= bit_max; ++bit) {
        let x = 0, y = 0;
        for (let i = 0; i < n; ++i) {
            if (nums[i] & (1 << bit)) {
                x += 1;
            }
            if (i >= 1 && (i & (1 << bit))) {
                y += 1;
            }
        }
        if (x > y) {
            ans |= 1 << bit;
        }
    }
    return ans;
};

[sol2-Java]

class Solution {
    public int findDuplicate(int[] nums) {
        int n = nums.length, ans = 0;
        int bit_max = 31;
        while (((n - 1) >> bit_max) == 0) {
            bit_max -= 1;
        }
        for (int bit = 0; bit <= bit_max; ++bit) {
            int x = 0, y = 0;
            for (int i = 0; i < n; ++i) {
                if ((nums[i] & (1 << bit)) != 0) {
                    x += 1;
                }
                if (i >= 1 && ((i & (1 << bit)) != 0)) {
                    y += 1;
                }
            }
            if (x > y) {
                ans |= 1 << bit;
            }
        }
        return ans;
    }
}

[sol2-Golang]

func findDuplicate(nums []int) int {
    n := len(nums)
    ans := 0
    bit_max := 31
    for ((n-1) >> bit_max) == 0 {
        bit_max--
    }
    for bit := 0; bit <= bit_max; bit++ {
        x, y := 0, 0
        for i := 0; i < n; i++ {
            if (nums[i] & (1 << bit)) > 0 {
                x++
            }
            if i >= 1 && (i & (1 << bit)) > 0 {
                y++
            }
        }
        if x > y {
            ans |= 1 << bit
        }
    }
    return ans
}

复杂度证明

• 时间复杂度：$O(n\log n)$，其中 $n$ 为 nums 数组的长度。$O(\log n)$ 代表了我们枚举二进制数的位数个数，枚举第 $i$ 位的时候需要遍历数组统计 $x$ 和 $y$ 的答案，因此总时间复杂度为 $O(n\log n)$。

• 空间复杂度：$O(1)$。我们只需要常数空间存放若干变量。

方法三：快慢指针

预备知识

本方法需要读者对 「Floyd 判圈算法」（又称龟兔赛跑算法）有所了解，它是一个检测链表是否有环的算法，LeetCode 中相关例题有 141. 环形链表 ，142. 环形链表 II 。

思路和算法

我们对 nums 数组建图，每个位置 $i$ 连一条 $i\rightarrow \textit{nums}[i]$ 的边。由于存在的重复的数字 target，因此 target 这个位置一定有起码两条指向它的边，因此整张图一定存在环，且我们要找到的 target 就是这个环的入口，那么整个问题就等价于 142. 环形链表 II 。

我们先设置慢指针 slow 和快指针 fast ，慢指针每次走一步，快指针每次走两步，根据「Floyd 判圈算法」两个指针在有环的情况下一定会相遇，此时我们再将 slow 放置起点 $0$，两个指针每次同时移动一步，相遇的点就是答案。

<,,,,,,,,,,,,,,,,,,,,,,,,>

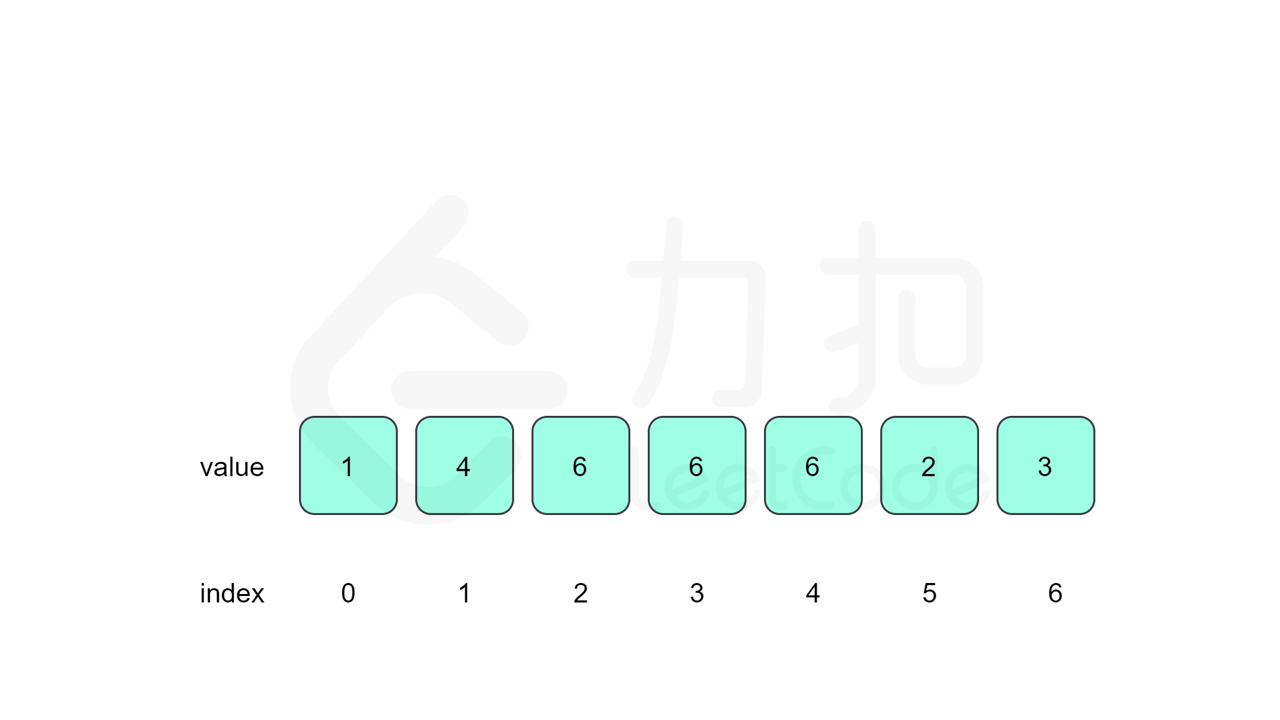
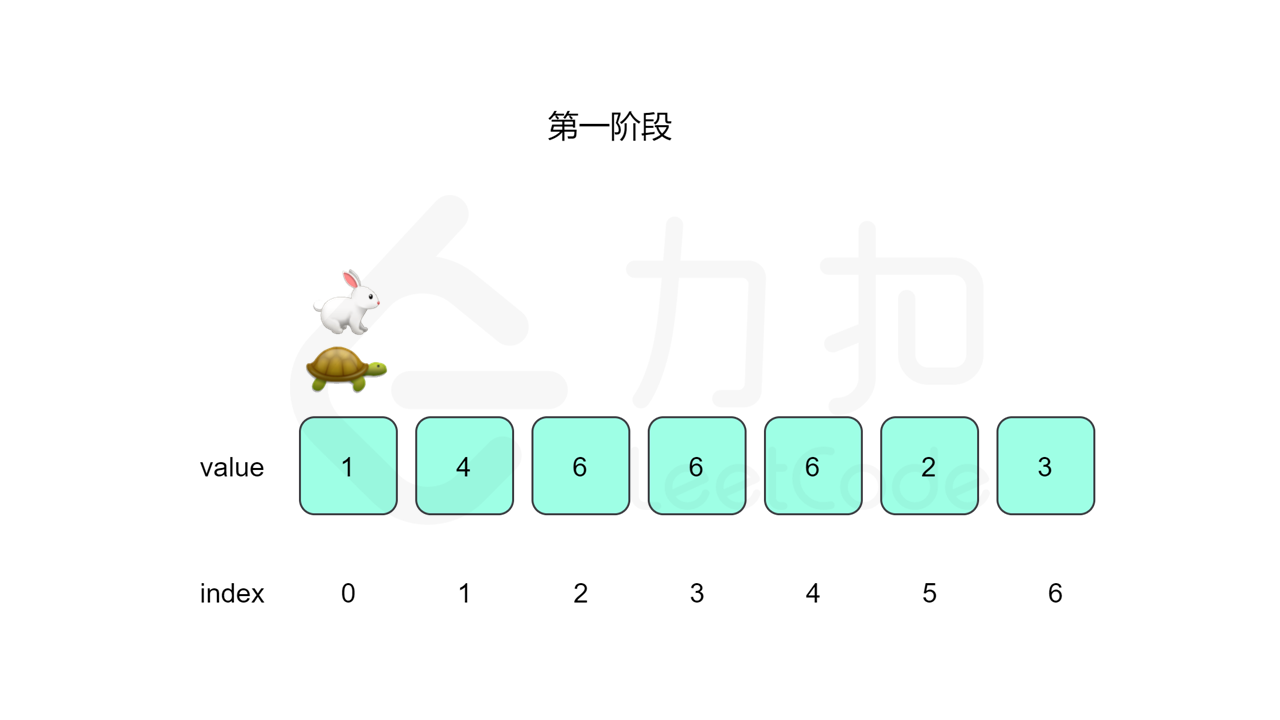
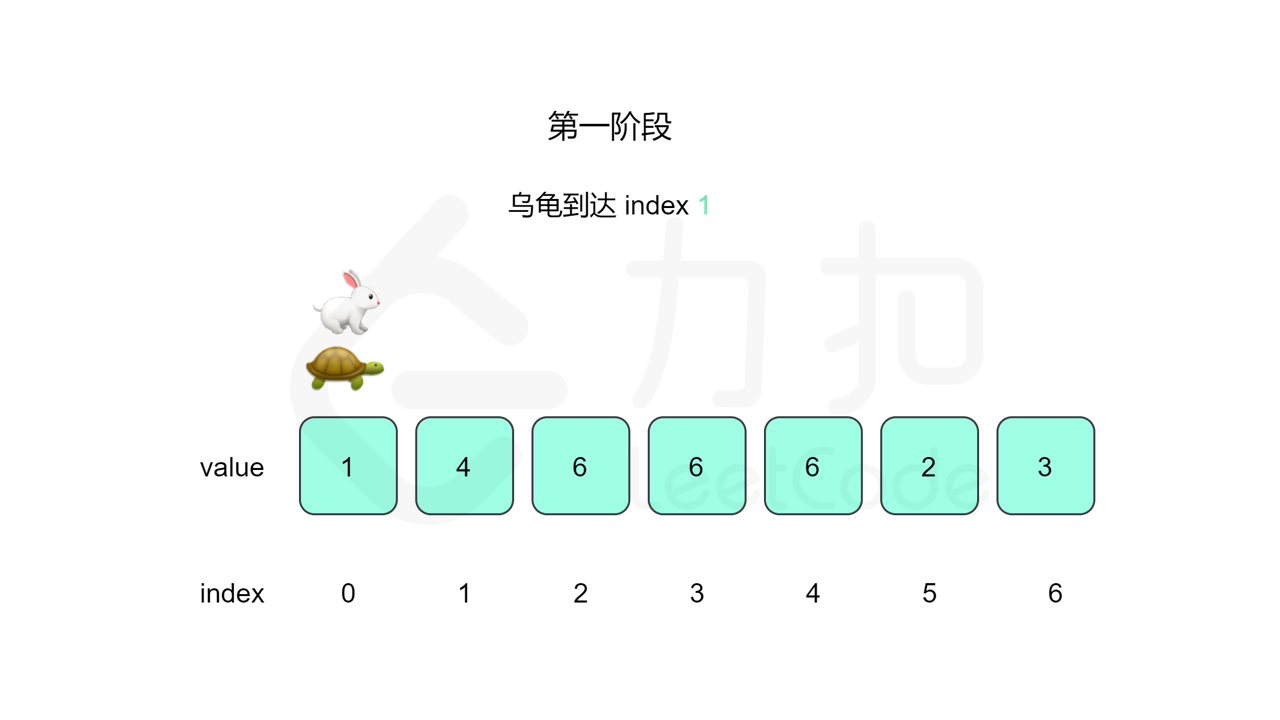
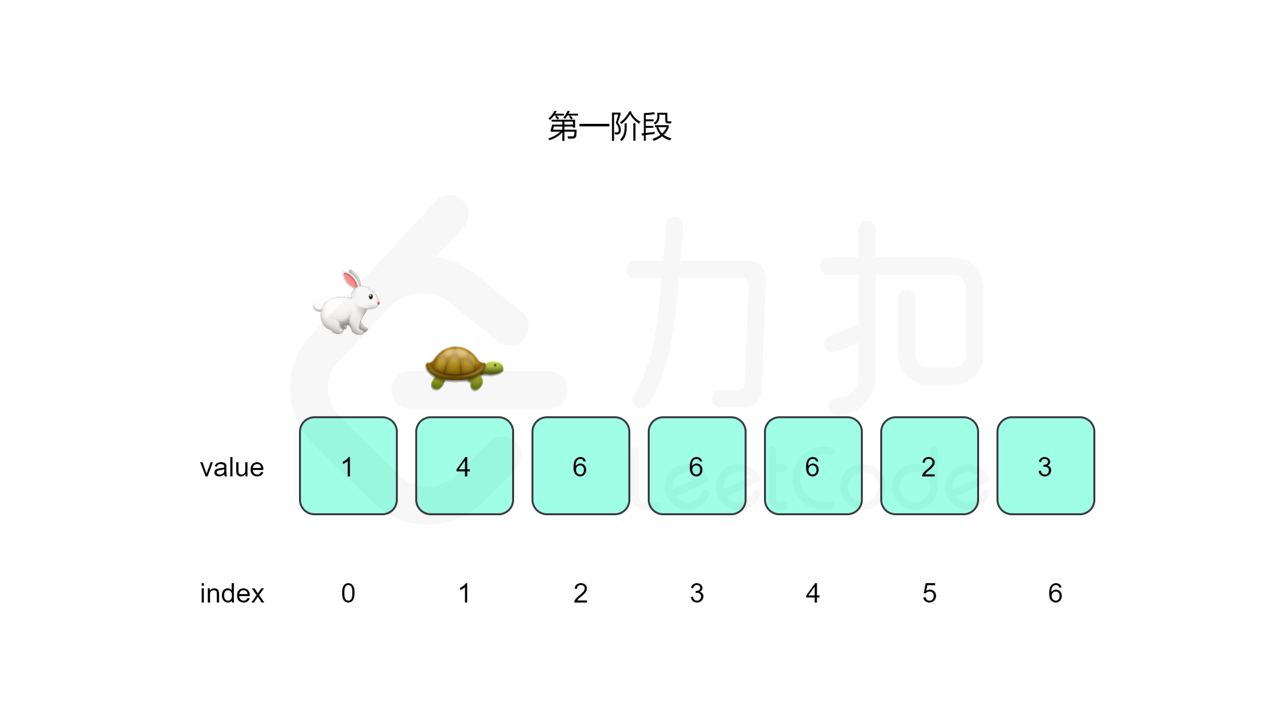
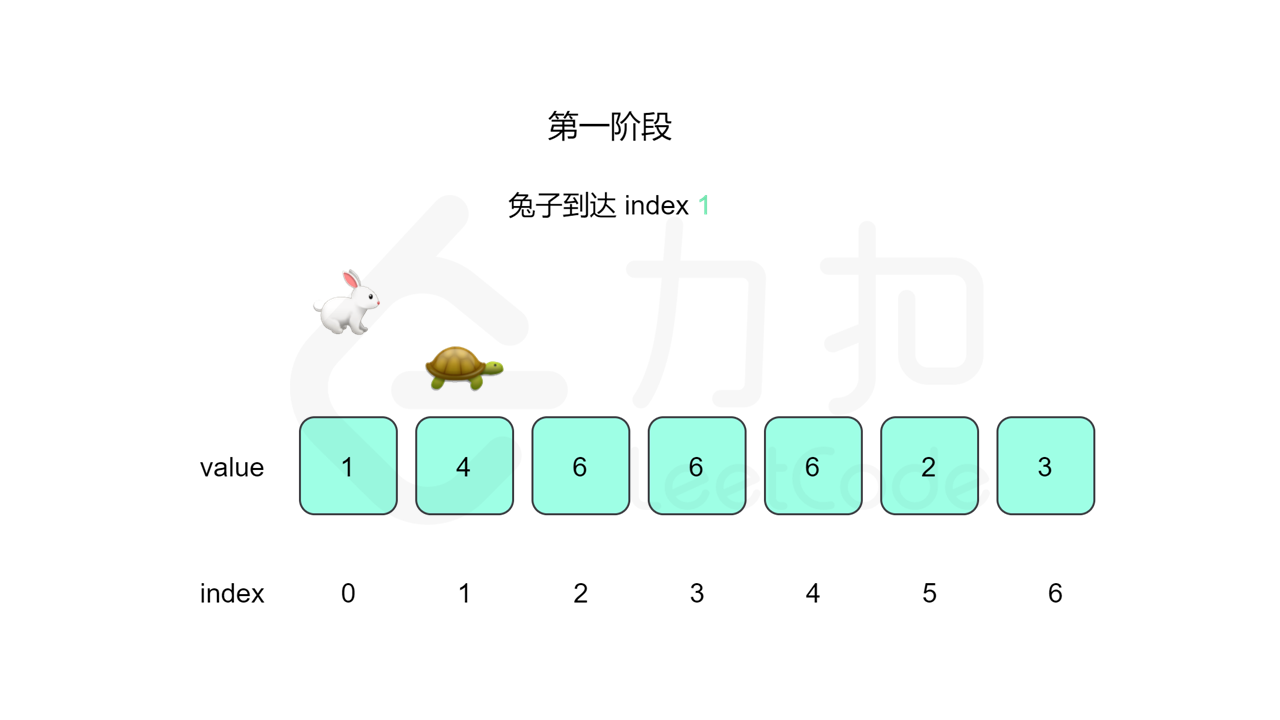
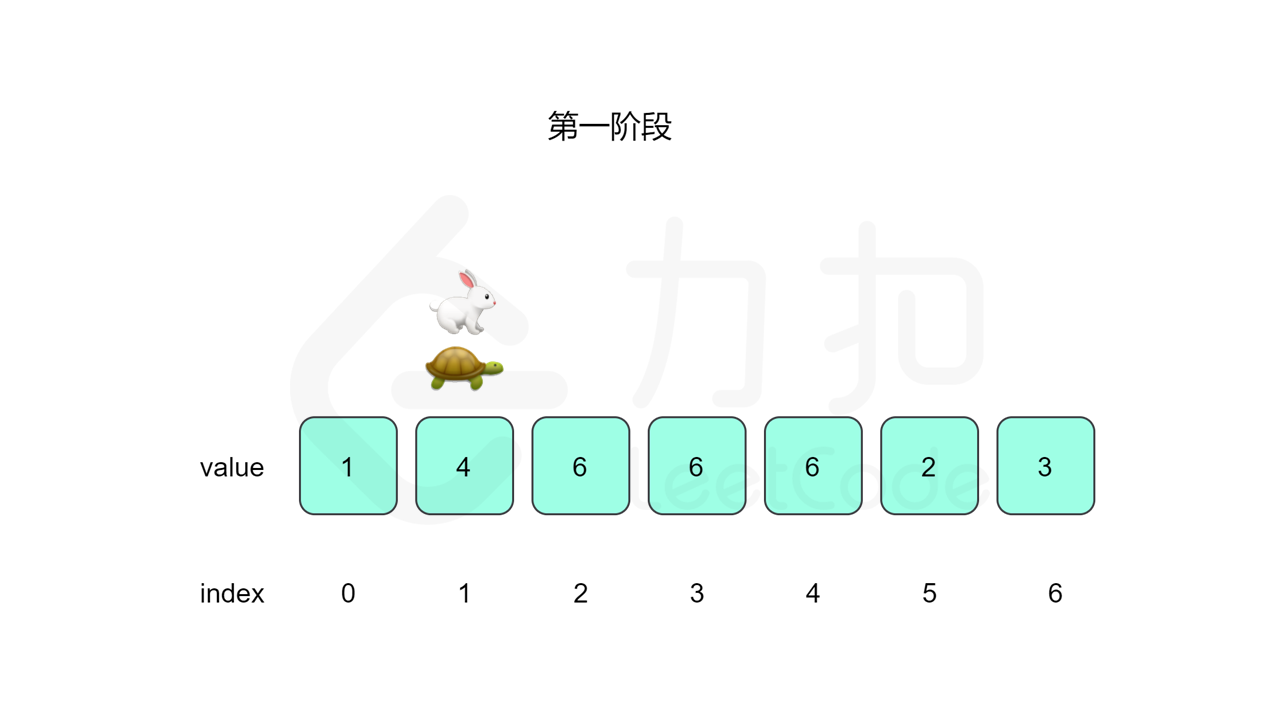
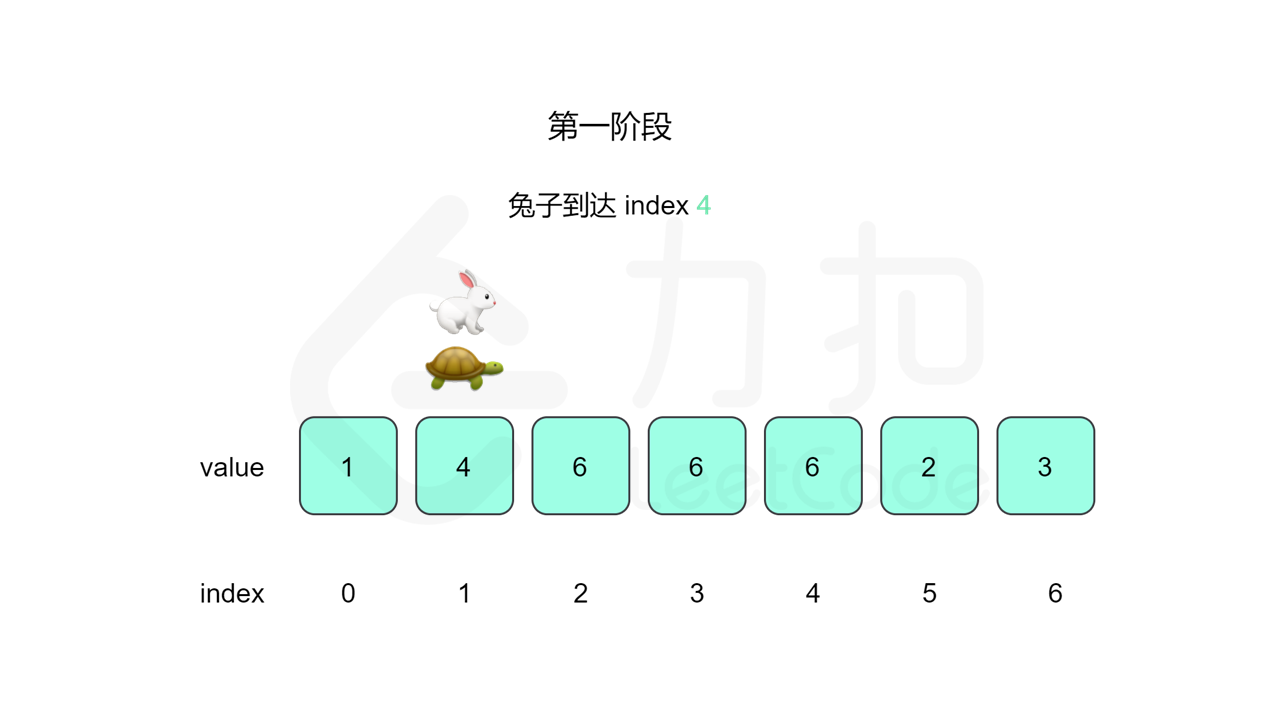
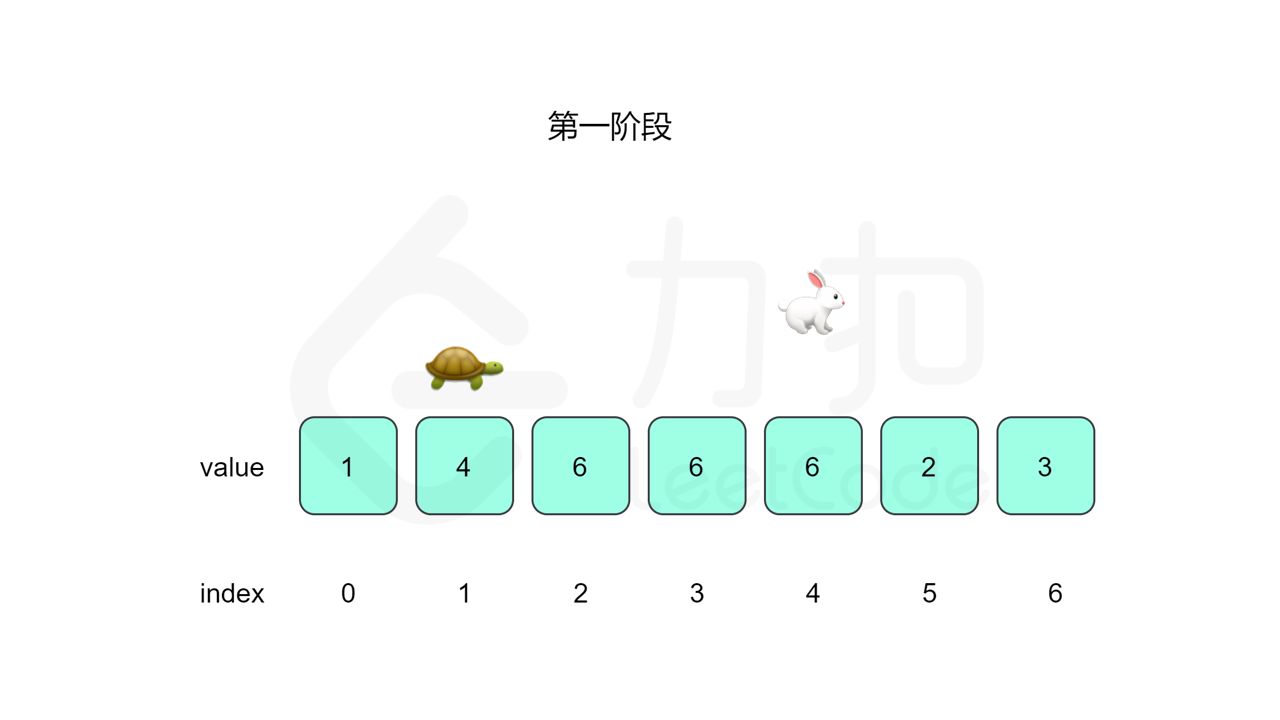
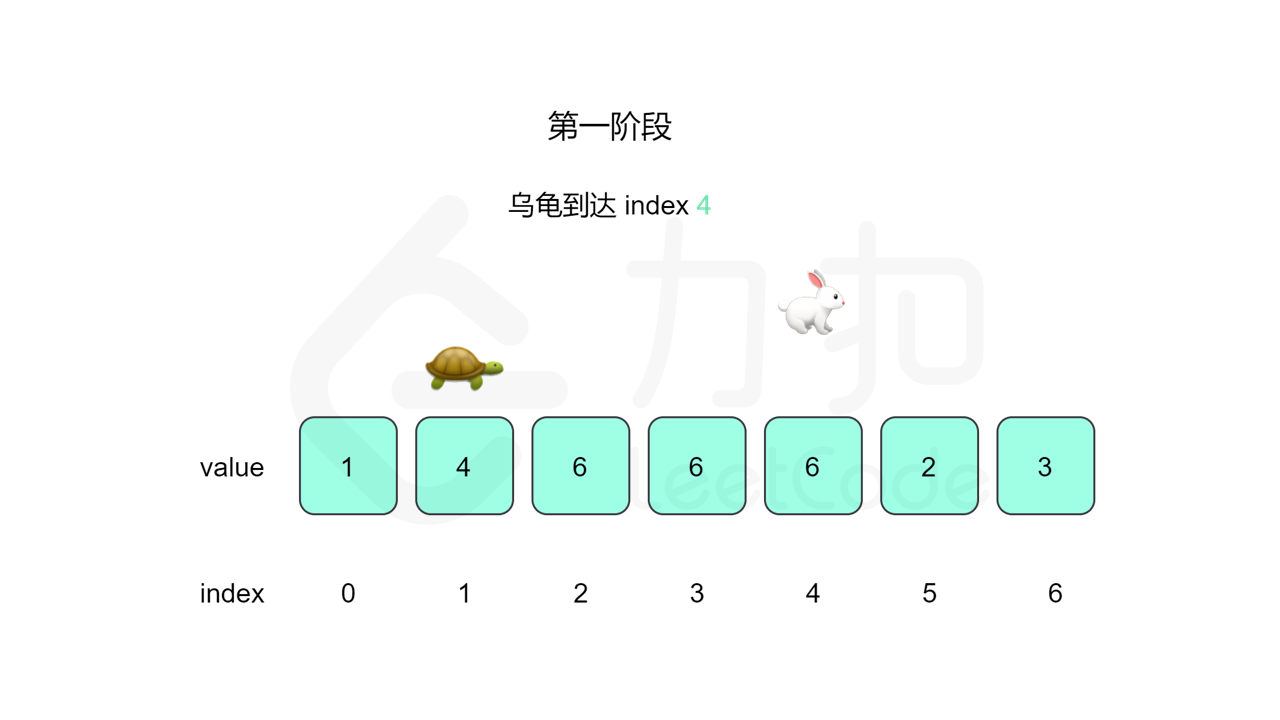
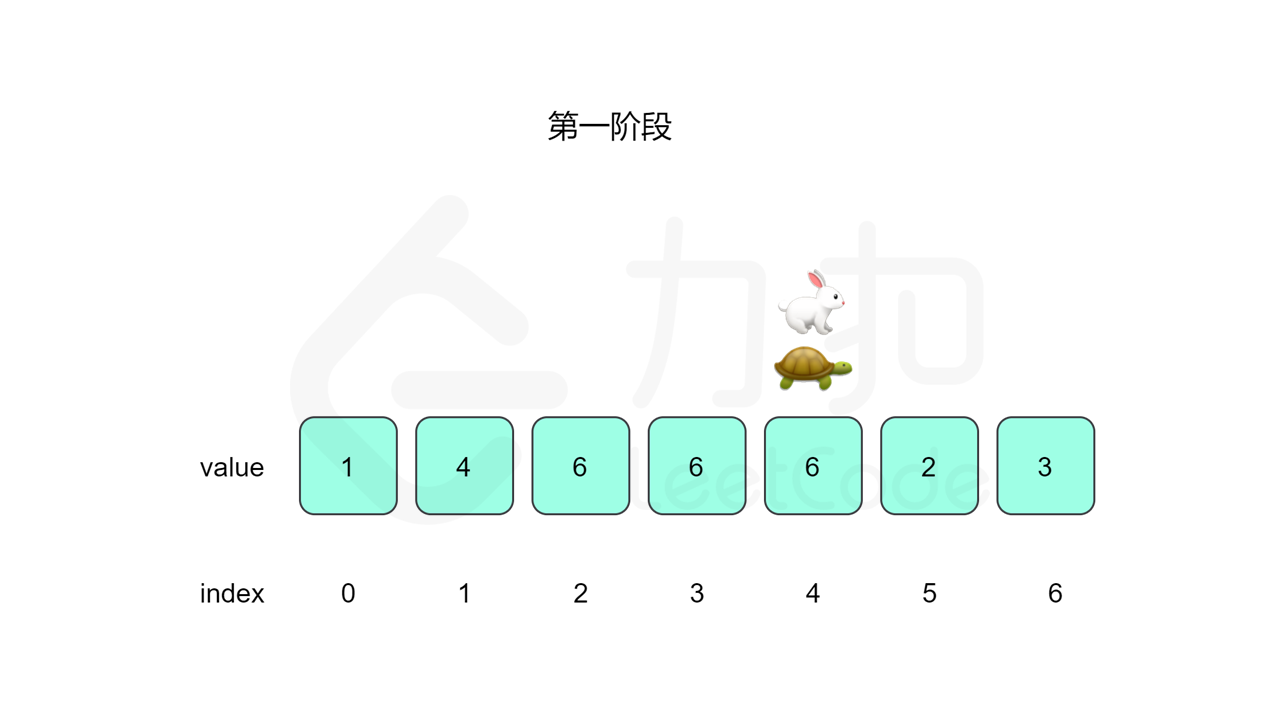
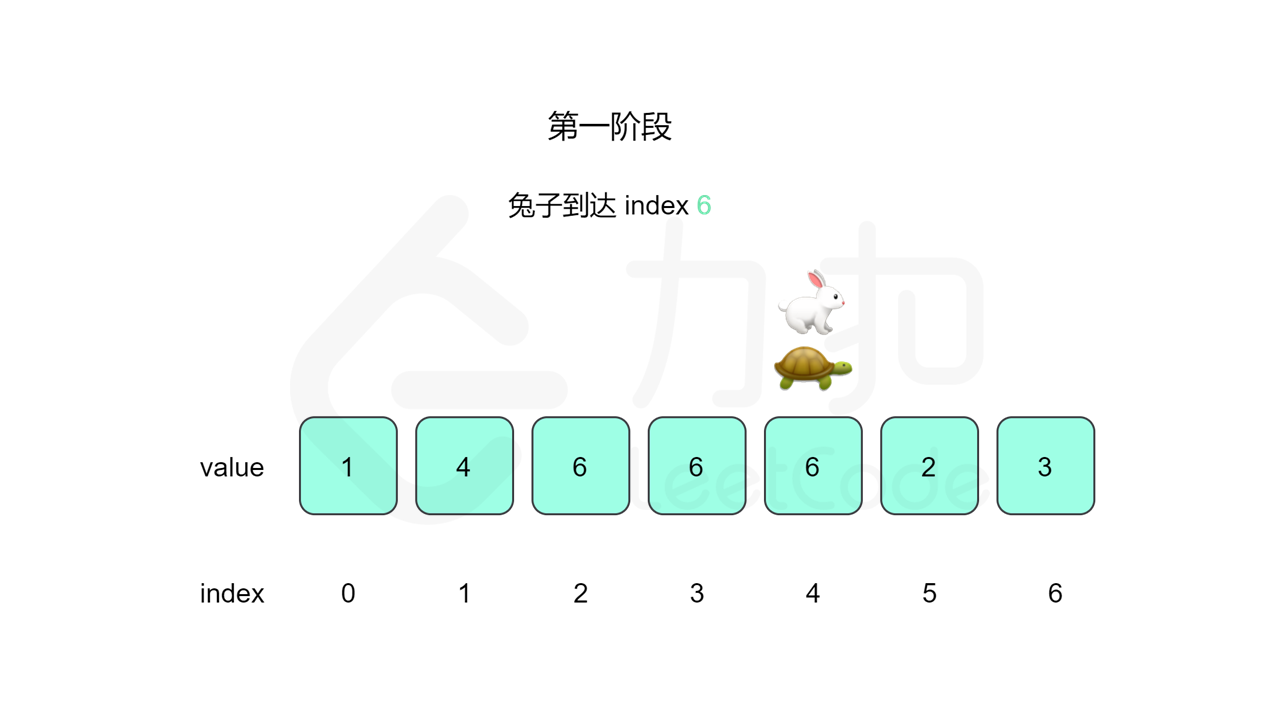
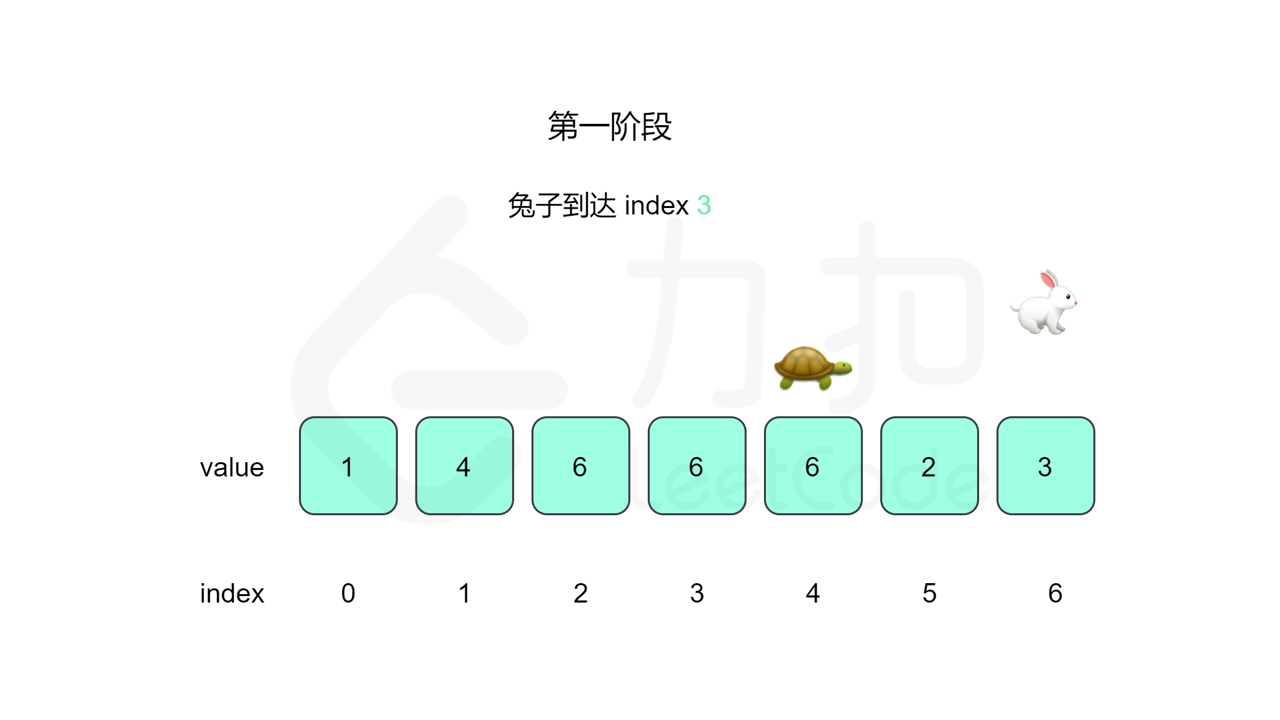
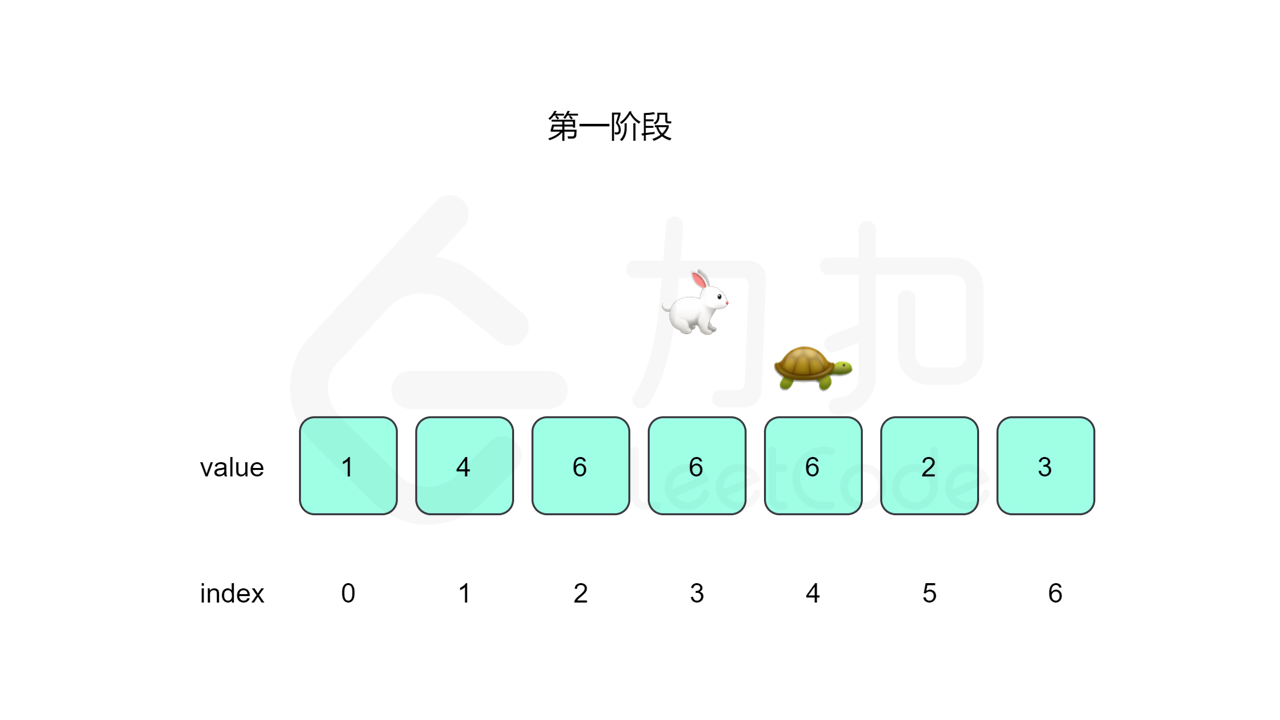
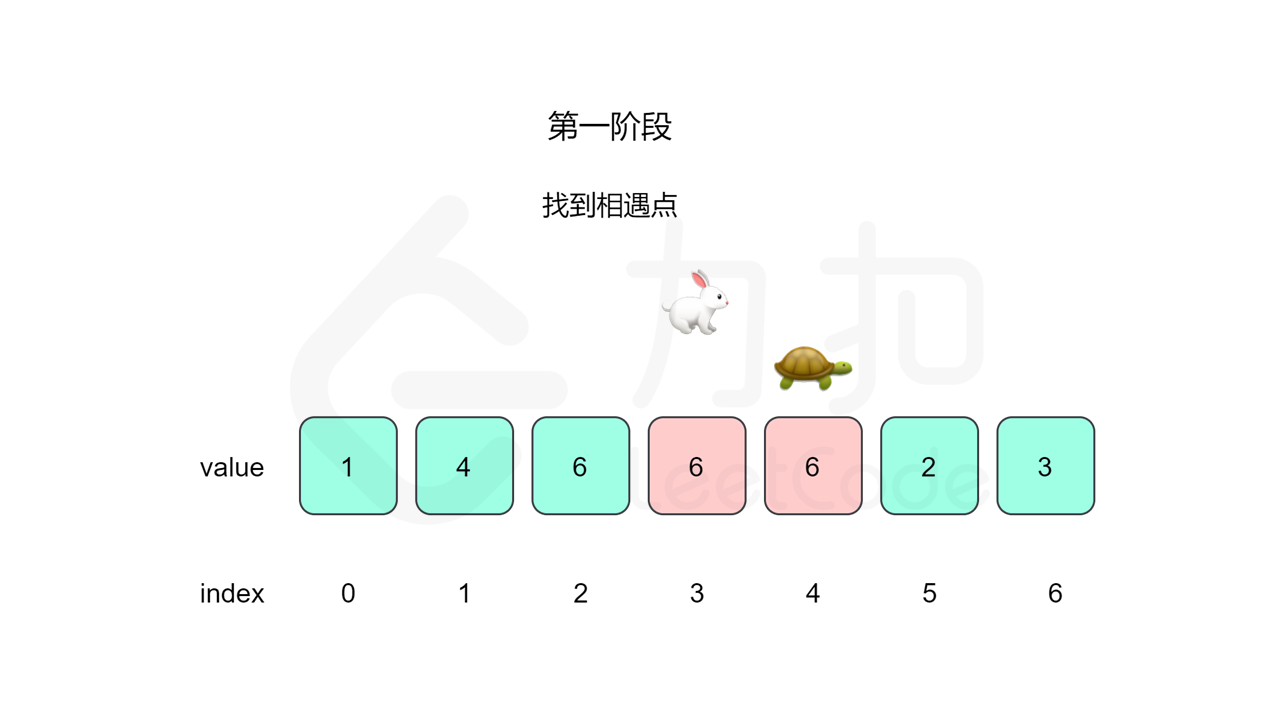
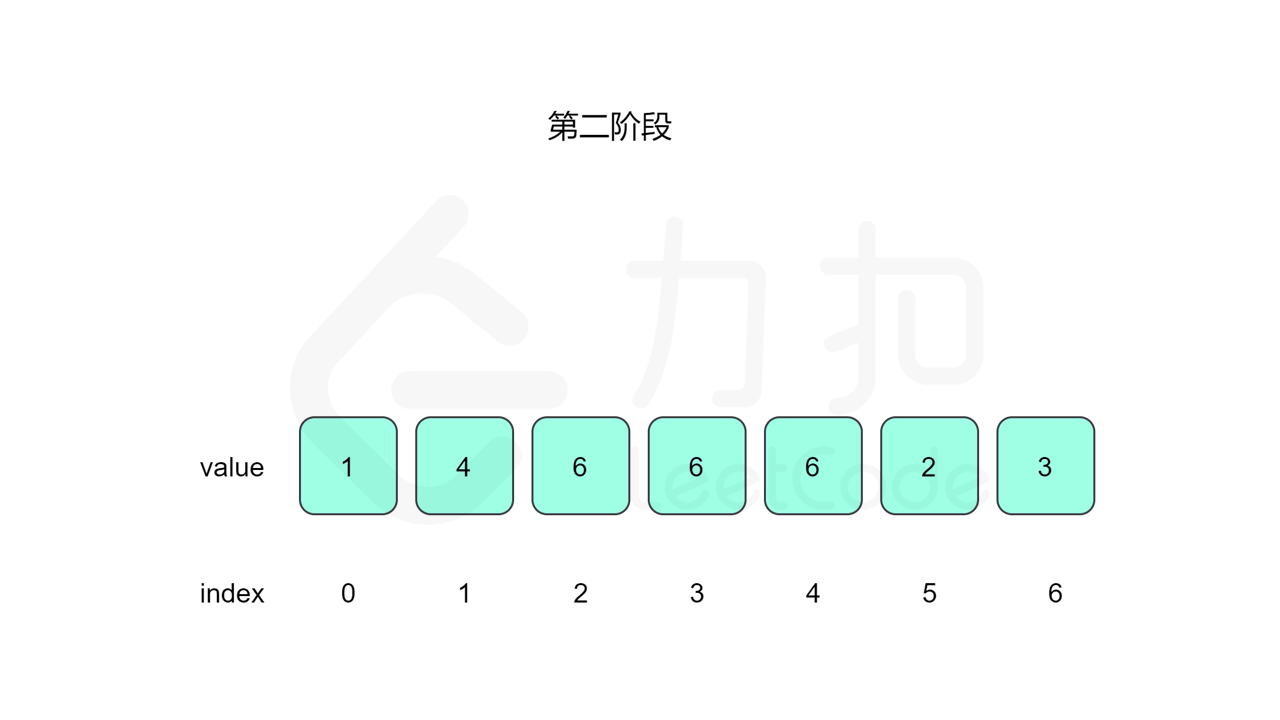
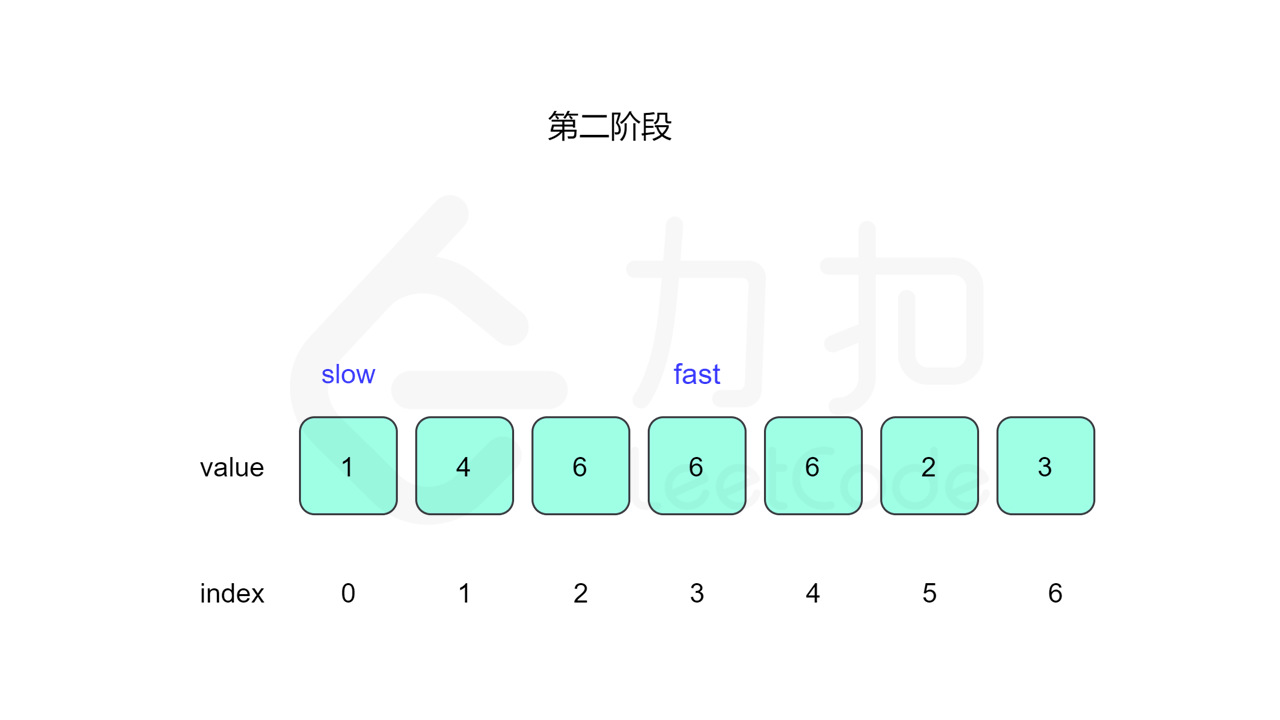
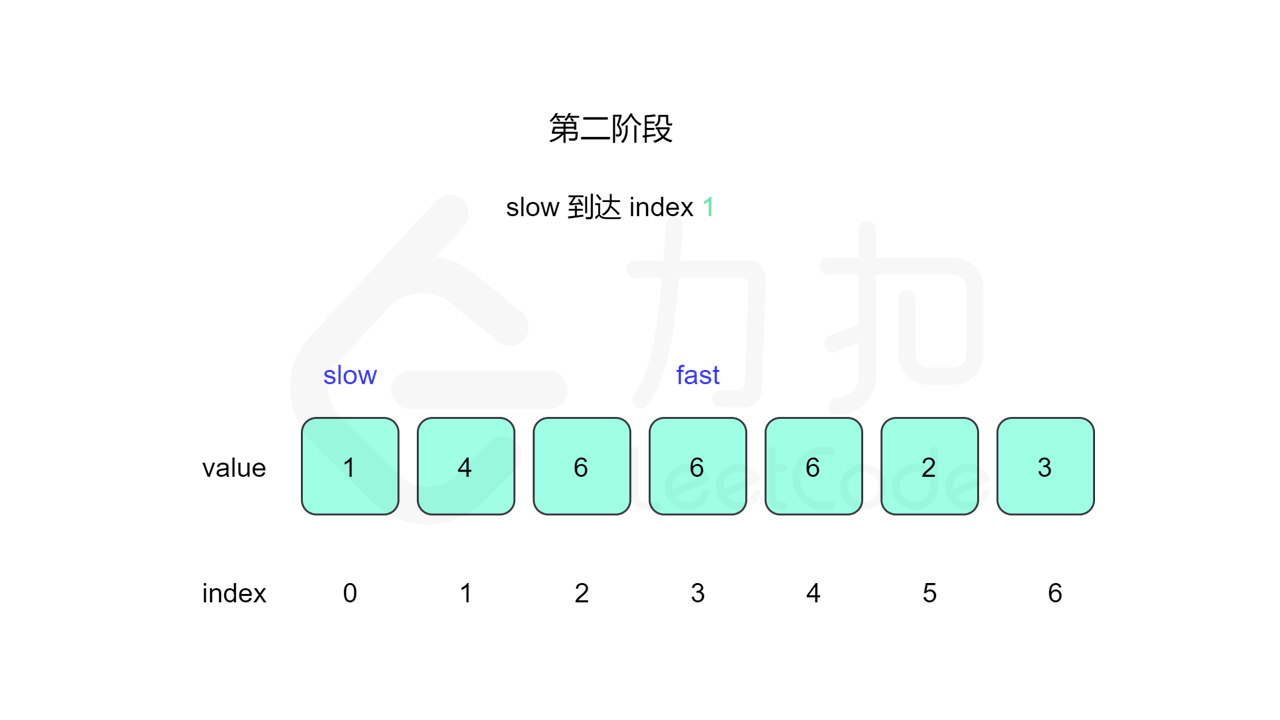
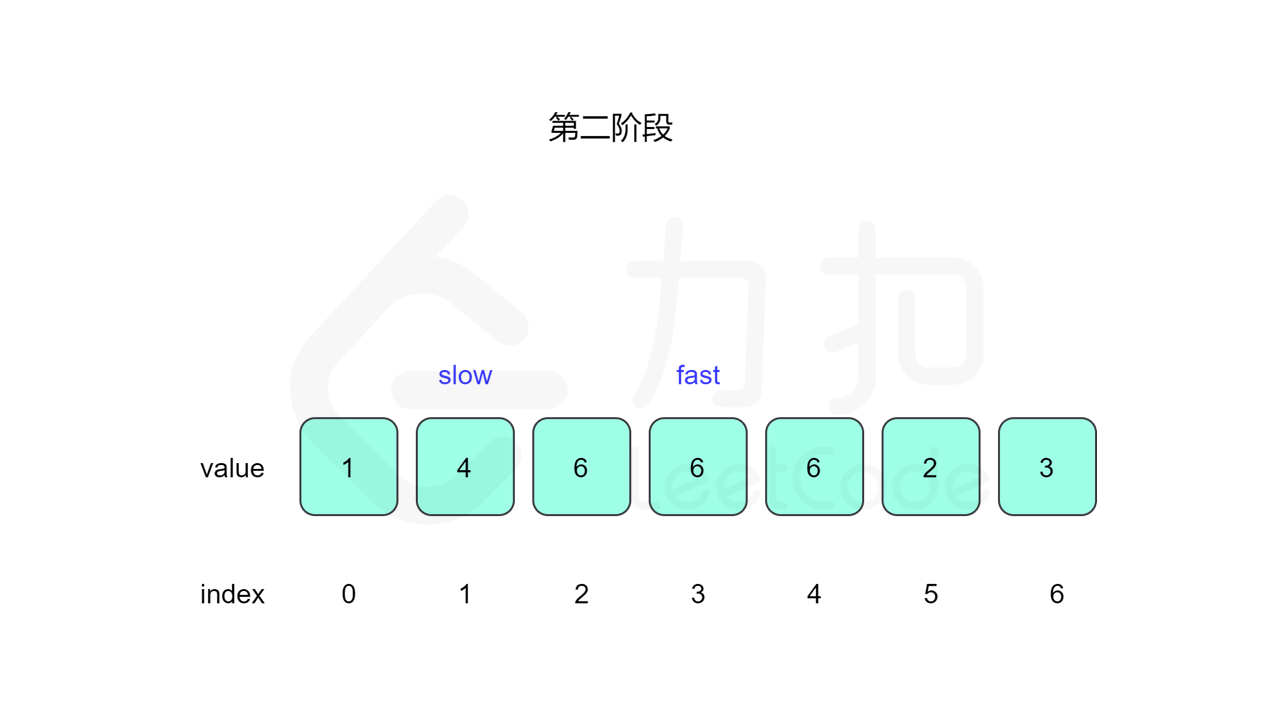
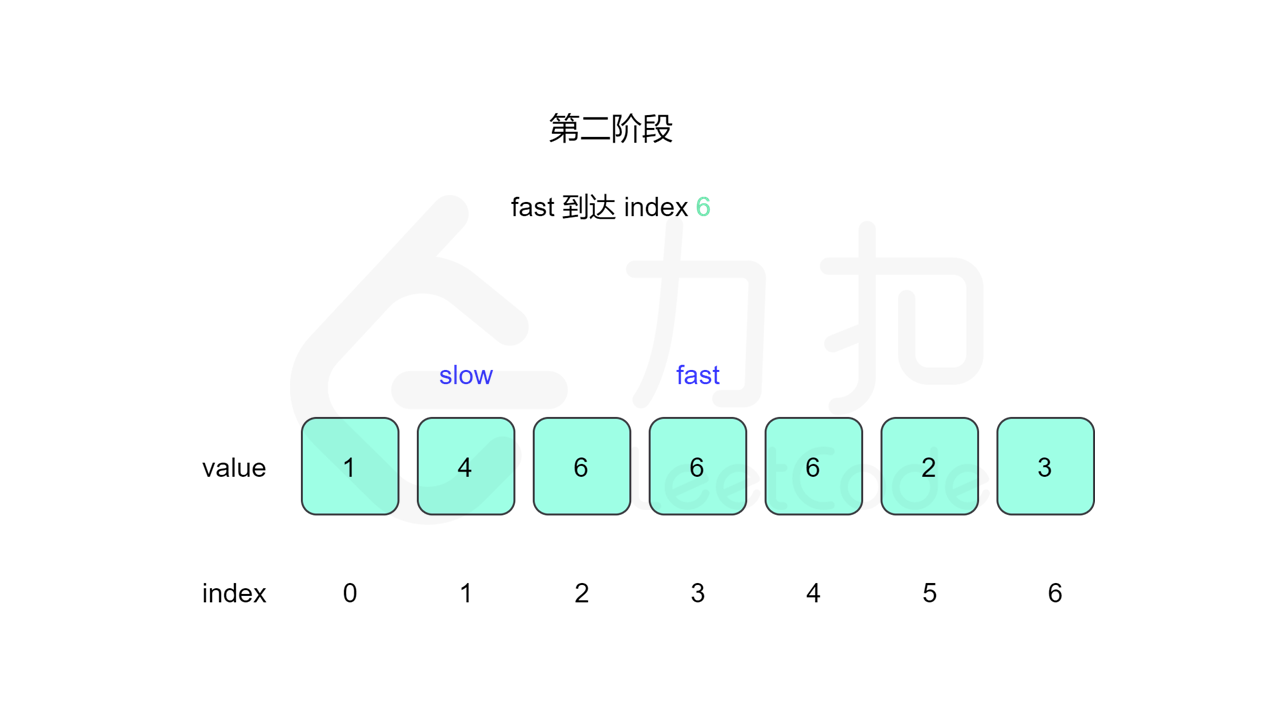
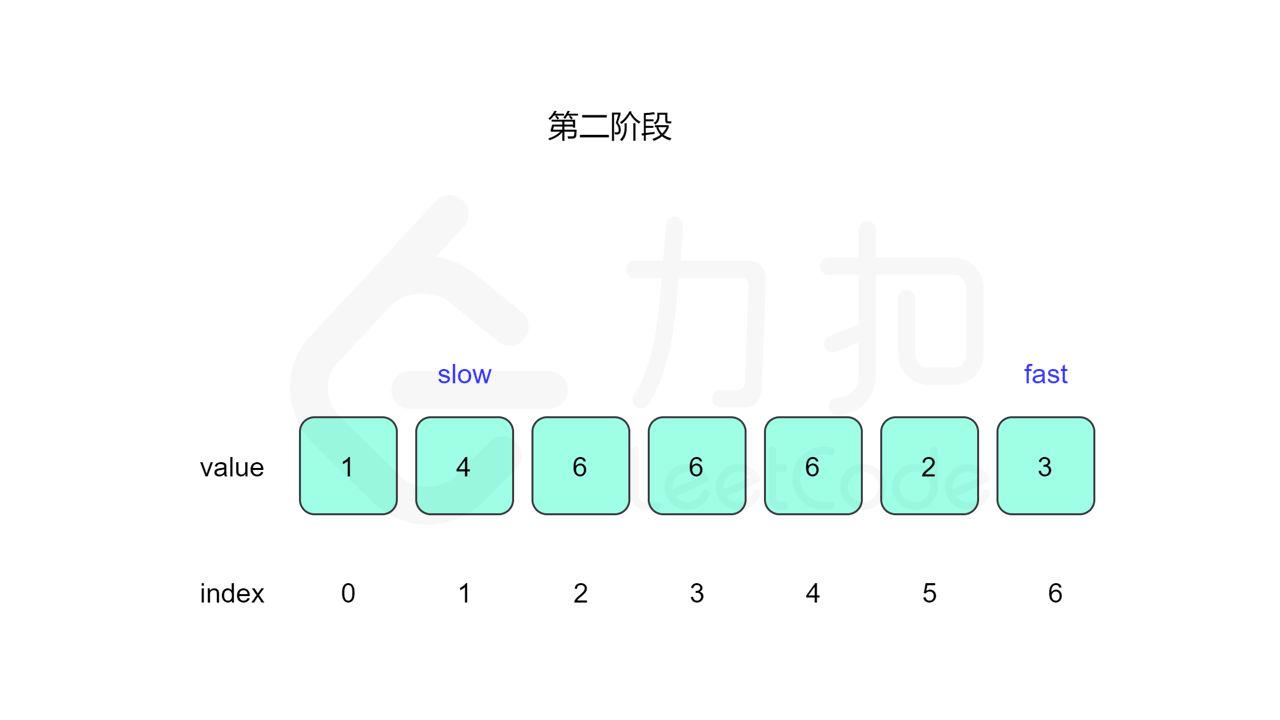
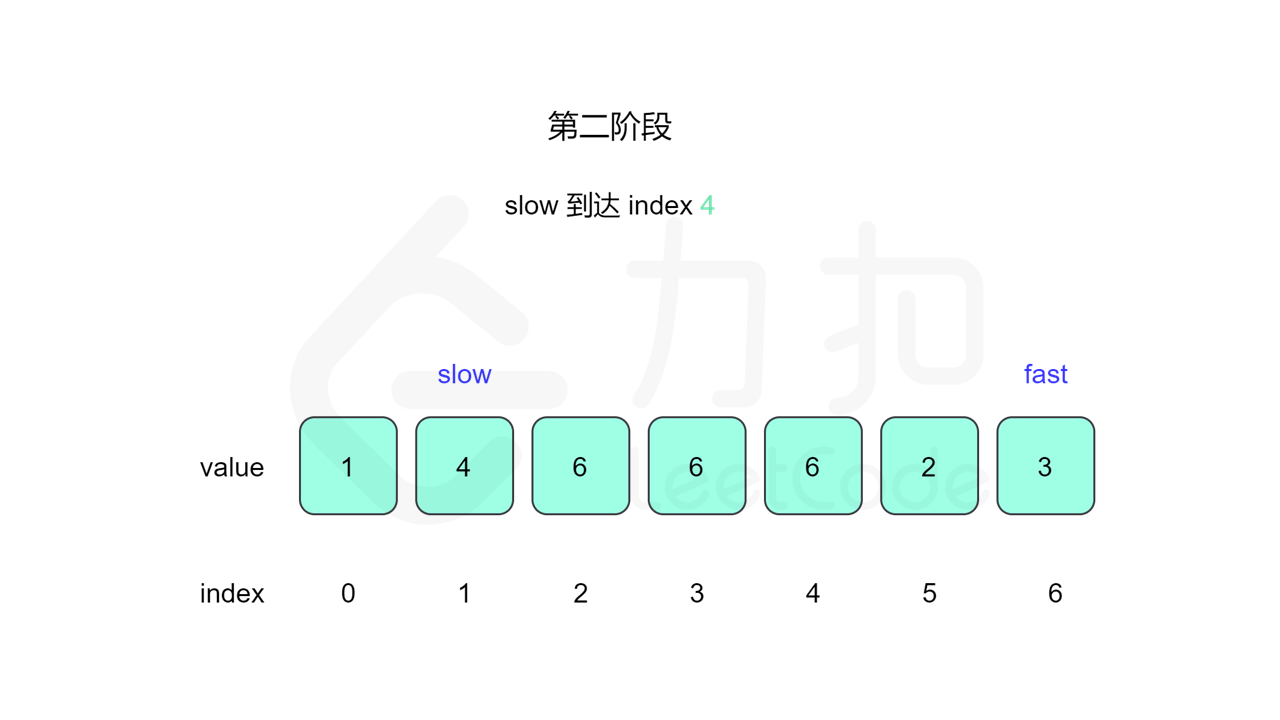
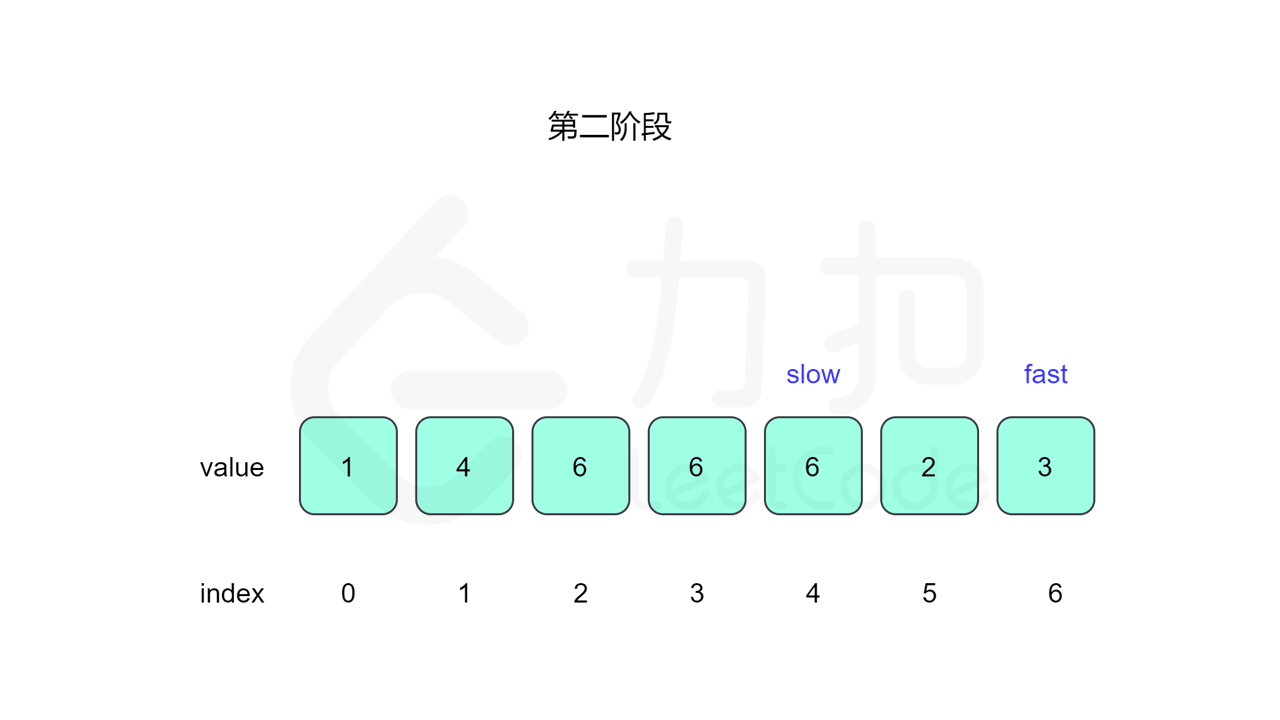
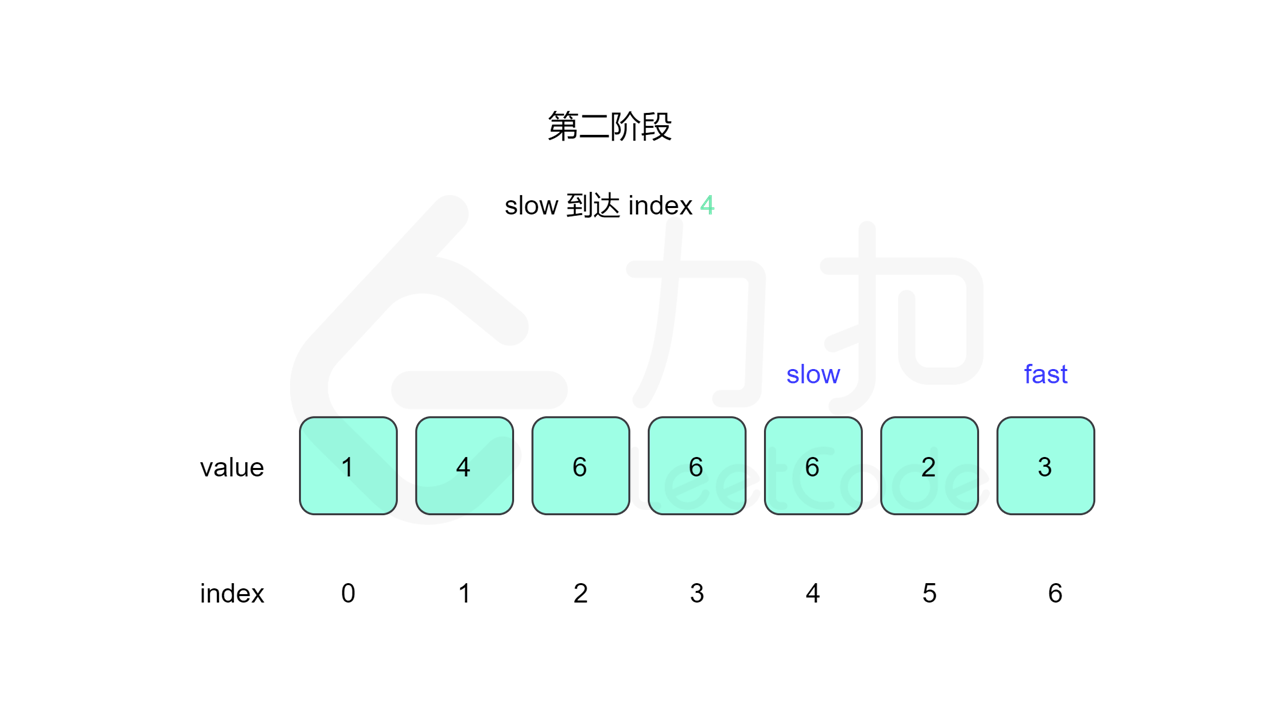
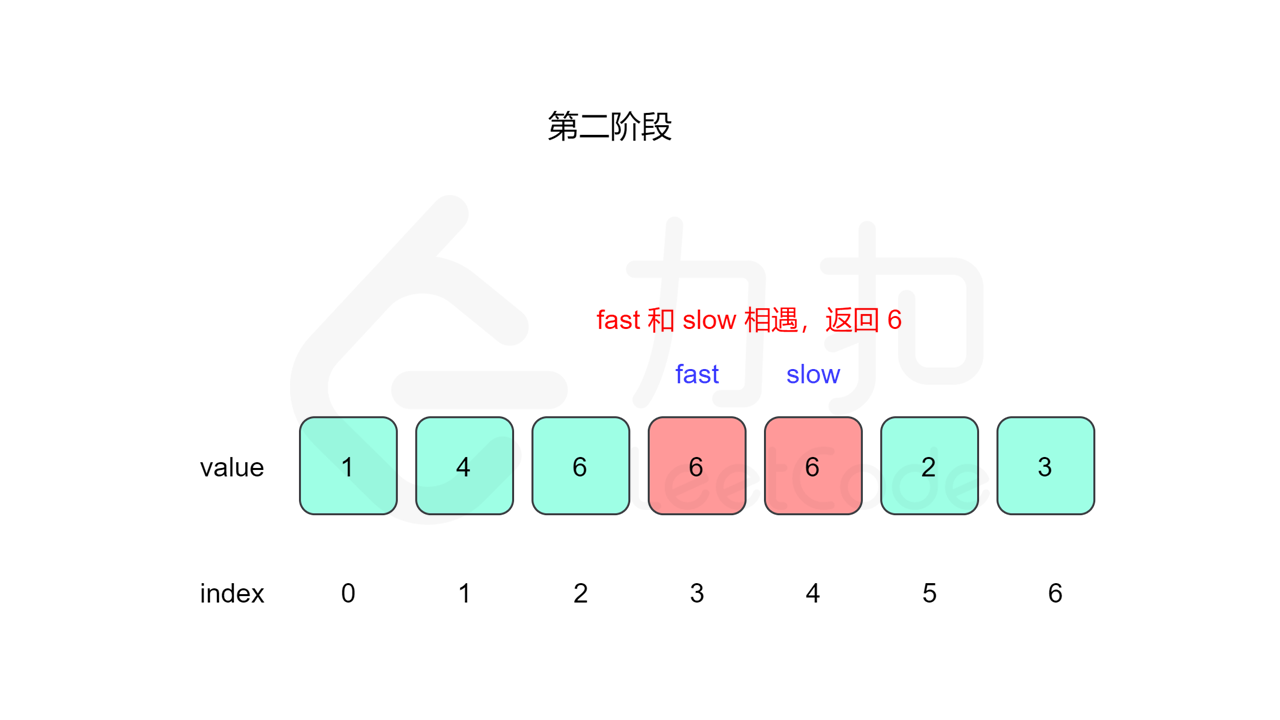
这里简单解释为什么后面将 slow 放置起点后移动相遇的点就一定是答案了。假设环长为 $L$，从起点到环的入口的步数是 $a$，从环的入口继续走 $b$ 步到达相遇位置，从相遇位置继续走 $c$ 步回到环的入口，则有 $b+c=L$，其中 $L$、$a$、$b$、$c$ 都是正整数。根据上述定义，慢指针走了 $a+b$ 步，快指针走了 $2(a+b)$ 步。从另一个角度考虑，在相遇位置，快指针比慢指针多走了若干圈，因此快指针走的步数还可以表示成 $a+b+kL$，其中 $k$ 表示快指针在环上走的圈数。联立等式，可以得到
$$
2(a+b)=a+b+kL
$$
解得 $a=kL-b$，整理可得
$$
a=(k-1)L+(L-b)=(k-1)L+c
$$
从上述等式可知，如果慢指针从起点出发，快指针从相遇位置出发，每次两个指针都移动一步，则慢指针走了 $a$ 步之后到达环的入口，快指针在环里走了 $k-1$ 圈之后又走了 $c$ 步，由于从相遇位置继续走 $c$ 步即可回到环的入口，因此快指针也到达环的入口。两个指针在环的入口相遇，相遇点就是答案。

[sol3-C++]

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int slow = 0, fast = 0;
        do {
            slow = nums[slow];
            fast = nums[nums[fast]];
        } while (slow != fast);
        slow = 0;
        while (slow != fast) {
            slow = nums[slow];
            fast = nums[fast];
        }
        return slow;
    }
};

[sol3-JavaScript]

var findDuplicate = function(nums) {
    let slow = 0, fast = 0;
    do {
        slow = nums[slow];
        fast = nums[nums[fast]];
    } while (slow != fast);
    slow = 0;
    while (slow != fast) {
        slow = nums[slow];
        fast = nums[fast];
    }
    return slow;
};

[sol3-Java]

class Solution {
    public int findDuplicate(int[] nums) {
        int slow = 0, fast = 0;
        do {
            slow = nums[slow];
            fast = nums[nums[fast]];
        } while (slow != fast);
        slow = 0;
        while (slow != fast) {
            slow = nums[slow];
            fast = nums[fast];
        }
        return slow;
    }
}

[sol3-Golang]

func findDuplicate(nums []int) int {
    slow, fast := 0, 0
    for slow, fast = nums[slow], nums[nums[fast]]; slow != fast; slow, fast = nums[slow], nums[nums[fast]] { }
    slow = 0
    for slow != fast {
        slow = nums[slow]
        fast = nums[fast]
    }
    return slow
}

复杂度分析

• 时间复杂度：$O(n)$。「Floyd 判圈算法」时间复杂度为线性的时间复杂度。

• 空间复杂度：$O(1)$。我们只需要常数空间存放若干变量。