0335-路径交叉

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 10:45:50 2023-09-13 10:45:50 Updated    

给你一个整数数组 distance __ 。

从 X-Y 平面上的点 (0,0) 开始，先向北移动 distance[0] 米，然后向西移动 distance[1] 米，向南移动
distance[2] 米，向东移动 distance[3] 米，持续移动。也就是说，每次移动后你的方位会发生逆时针变化。

判断你所经过的路径是否相交。如果相交，返回 true ；否则，返回 false 。

示例 1：

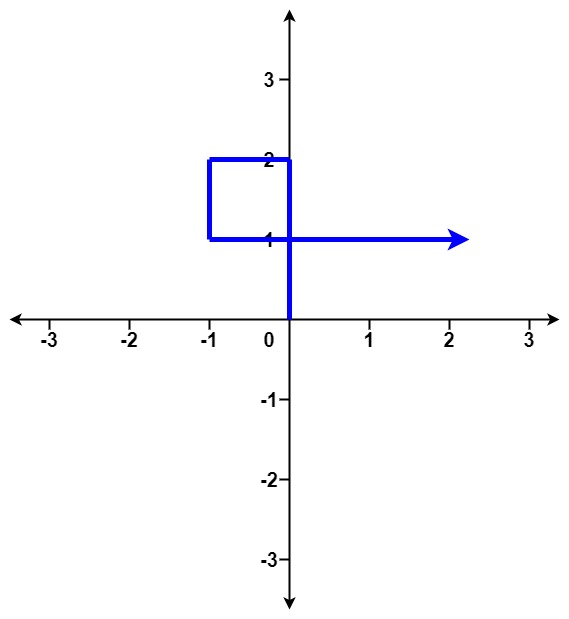
**输入：** distance = [2,1,1,2]
**输出：** true

示例 2：

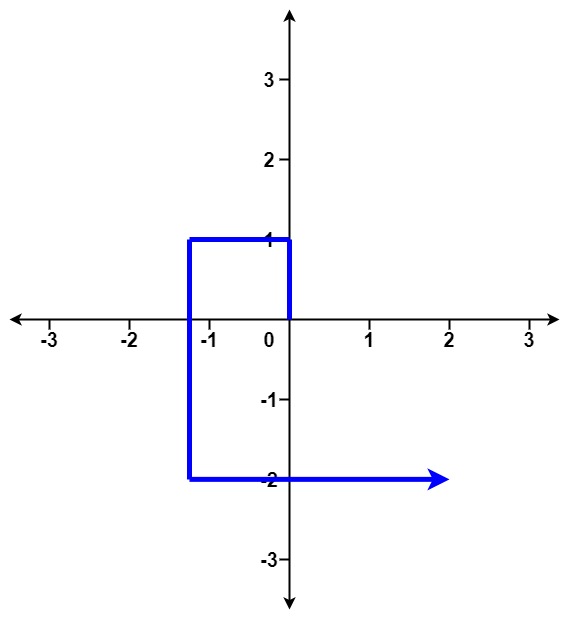
**输入：** distance = [1,2,3,4]
**输出：** false

示例 3：

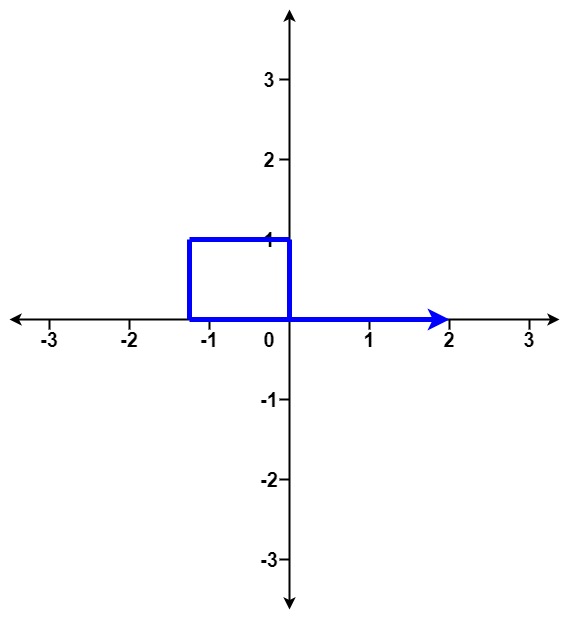
**输入：** distance = [1,1,1,1]
**输出：** true

提示：

  • 1 <= distance.length <= 105
  • 1 <= distance[i] <= 105

前言

我们先通过枚举各种移动方案来归纳路径交叉的规律。

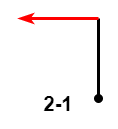
第 $1$ 次移动和第 $2$ 次移动的情况：

因为这两次移动都是各自方向上的第一次移动，所以这两次移动距离将作为之后移动距离的参考系，但本身没有意义。因此，此时只有 $2-1$ 一种情况。

2_1

第 $3$ 次移动的情况：

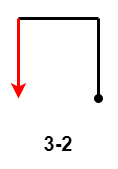
此时一定是 $2-1$，第 $3$ 次移动距离相较于第 $1$ 次移动距离，有三种情况：

  • $3-1$：第 $3$ 次移动距离小于第 $1$ 次移动距离；
  • $3-2$：第 $3$ 次移动距离等于第 $1$ 次移动距离；
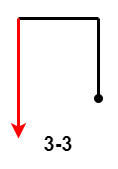
  • $3-3$：第 $3$ 次移动距离大于第 $1$ 次移动距离。

3_1 3_2 3_3

第 $4$ 次移动的情况：

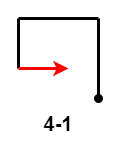
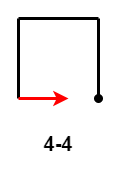
当前 $3$ 次移动是 $3-1$ 时，第 $4$ 次移动距离相较于第 $2$ 次移动距离，有两种情况：

  • $4-1$：第 $4$ 次移动距离小于第 $2$ 次移动距离；
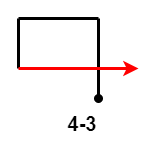
  • $4-2$ 和 $4-3$：第 $4$ 次移动距离大于等于第 $2$ 次移动距离相同，出现路径交叉。

4_1 4_2 4_3

根据以上结果，我们发现 $3-1$ 具有如下性质：如果在当前的第 $i$ 次移动之后，存在第 $j$ 次移动（$j > i$）的距离大于等于第 $j-2$ 次移动的距离，则会出现路径交叉。另外，我们发现 $4-1$ 具有和 $3-1$ 相同的性质，于是 $4-1$ 等价于 $3-1$；不需要继续讨论 $4-1$ 的后续情况。

当前 $3$ 次移动是 $3-2$ 时，第 $4$ 次移动距离相较于第 $2$ 次移动距离，有两种情况：

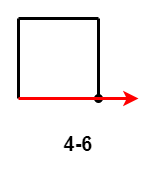
  • $4-4$：第 $4$ 次移动距离小于第 $2$ 次移动距离；
  • $4-5$ 和 $4-6$：第 $4$ 次移动距离大于等于第 $2$ 次移动距离，出现路径交叉。

4_4 4_5 4_6

根据以上结果，我们发现 $3-2$ 具有和 $3-1$ 相同的性质，于是 $4-4$ 等价于 $3-2$，并间接地等价于 $3-1$；不需要继续讨论 $4-4$ 的后续情况。

当前 $3$ 次移动是 $3-3$ 时，第 $4$ 次移动距离相较于第 $2$ 次移动距离，有三种情况：

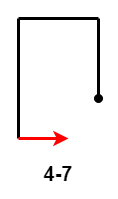
  • $4-7$：第 $4$ 次移动距离小于第 $2$ 次移动距离；
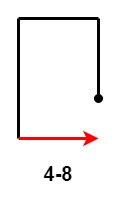
  • $4-8$：第 $4$ 次移动距离等于第 $2$ 次移动距离；
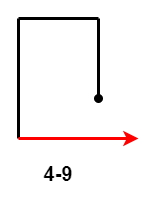
  • $4-9$：第 $4$ 次移动距离大于第 $2$ 次移动距离。

4_7 4_8 4_9

根据以上结果，我们发现 $4-7$ 也具有和 $3-1$ 相同的性质，于是 $4-7$ 等价于 $3-1$；不需要继续讨论 $4-7$ 的后续情况。

第 $5$ 次移动的情况：

此时还需要讨论前 $4$ 次移动是 $4-8$ 或 $4-9$ 的情况。

当前 $4$ 次移动是 $4-8$ 时，第 $5$ 次移动距离相较于第 $3$ 次移动距离和第 $1$ 次移动距离，有两种情况：

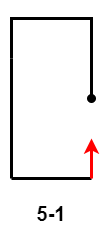
  • $5-1$：第 $5$ 次移动距离小于第 $3$ 次移动距离减第 $1$ 次移动距离的差；
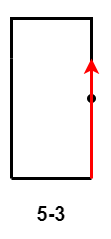
  • $5-2$ 和 $5-3$：第 $5$ 次移动距离大于等于第 $3$ 次移动距离减第 $1$ 次移动距离的差，出现路径交叉。

5_1 5_2 5_3

根据以上结果，我们发现 $5-1$ 也具有和 $3-1$ 相同的性质，于是 $5-1$ 等价于 $3-1$；不需要继续讨论 $5-1$ 的后续情况。

当前 $4$ 次移动是 $4-9$ 时，第 $5$ 次移动距离相较于第 $3$ 次移动距离和第 $1$ 次移动距离，有三种情况：

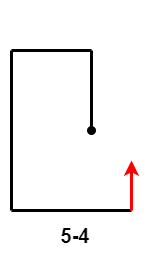
  • $5-4$：第 $5$ 次移动距离小于第 $3$ 次移动距离减第 $1$ 次移动距离的差；
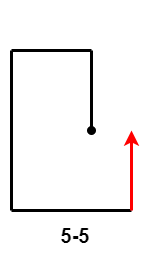
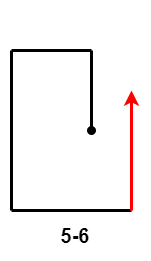
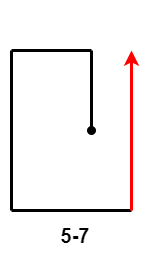
  • $5-5$、$5-6$ 和 $5-7$：第 $5$ 次移动距离大于等于第 $3$ 次移动距离减第 $1$ 次移动距离的差，且小于等于第 $3$ 次移动距离；
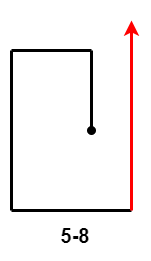
  • $5-8$：第 $5$ 次移动距离大于第 $3$ 次移动距离。

5_4 5_5 5_6 5_7 5_8

根据以上结果，我们发现 $5-4$ 也具有和 $3-1$ 相同的性质，于是 $5-1$ 等价于 $3-1$；不需要继续讨论 $5-4$ 的后续情况。

第 $6$ 次移动的情况：

此时还需要讨论前 $5$ 次移动是 $5-5$、$5-6$ 或 $5-7$ 的情况，以及前 $5$ 次移动是 $5-8$ 的情况。

当前 $5$ 次移动是 $5-5$、$5-6$ 或 $5-7$ 时，我们不妨以 $5-6$ 为例，第 $6$ 次移动距离相较于第 $4$ 次移动距离和第 $2$ 次移动距离，有两种情况：

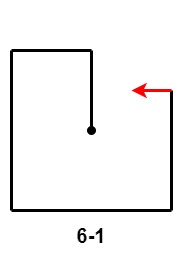
  • $6-1$：第 $6$ 次移动距离小于第 $4$ 次移动距离减第 $2$ 次移动距离的差；
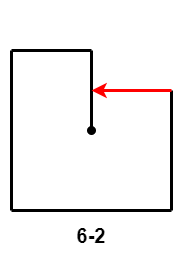
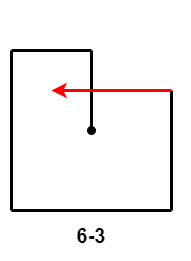
  • $6-2$ 和 $6-3$：第 $6$ 次移动距离大于等于第 $4$ 次移动距离减第 $2$ 次移动距离的差，出现路径交叉。

6_1 6_2 6_3

根据以上结果，我们发现 $6-1$ 也具有和 $3-1$ 相同的性质，于是 $6-1$ 等价于 $3-1$；不需要继续讨论 $6-1$ 的后续情况。

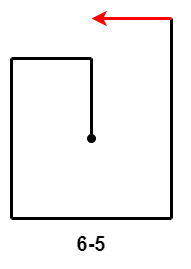
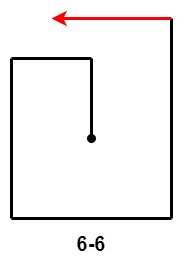
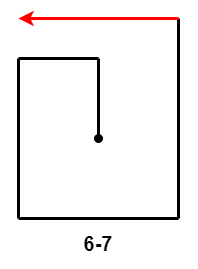
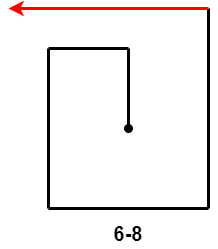
当前 $5$ 次移动是 $5-8$ 时，第 $6$ 次移动距离相较于第 $4$ 次移动距离和第 $2$ 次移动距离，有三种情况：

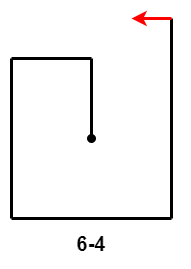
  • $6-4$：第 $6$ 次移动距离小于第 $4$ 次移动距离减第 $2$ 次移动距离的差；
  • $6-5$、$6-6$ 和 $6-7$：第 $6$ 次移动距离大于等于第 $4$ 次移动距离减第 $2$ 次移动距离的差，且小于等于第 $4$ 次移动距离；
  • $6-8$：第 $6$ 次移动距离大于第 $4$ 次移动距离。

6_4 6_5 6_6 6_7 6_8

根据以上结果，我们发现 $6-4$ 与 $5-4$ 的情况类似，都具有 $3-1$ 的性质；$6-5$、$6-6$、$6-7$ 与 $5-5$、$5-6$、$5-7$ 的情况类似，后续可能出现的情况类似于 $6-1$、$6-2$ 和 $6-3$；$6-8$ 与 $5-8$ 的情况类似，后续可能出现的情况类似 $6-4$、$6-5$、$6-6$、$6-7$ 和 $6-8$。

至此，我们已经通过归纳基本得到了路径交叉的规律。

方法一：归纳法（归纳路径交叉的情况）

思路和算法

根据归纳结果，我们发现所有可能的路径交叉的情况只有以下三类：

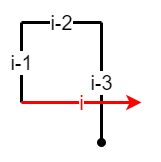
cross_1

第 $1$ 类，如上图所示，第 $i$ 次移动和第 $i-3$ 次移动（包含端点）交叉的情况，例如归纳中的 $4-2$、$4-3$、$4-5$ 和 $4-6$。

这种路径交叉需满足以下条件：

  • 第 $i-1$ 次移动距离小于等于第 $i-3$ 次移动距离。
  • 第 $i$ 次移动距离大于等于第 $i-2$ 次移动距离。

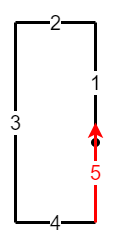
cross_2

第 $2$ 类，如上图所示，第 $5$ 次移动和第 $1$ 次移动交叉（重叠）的情况，例如归纳中的 $5-2$ 和 $5-3$。这类路径交叉的情况实际上是第 $3$ 类路径交叉在边界条件下的一种特殊情况。

这种路径交叉需要满足以下条件：

  • 第 $4$ 次移动距离等于第 $2$ 次移动距离。
  • 第 $5$ 次移动距离大于等于第 $3$ 次移动距离减第 $1$ 次移动距离的差；注意此时第 $3$ 次移动距离一定大于第 $1$ 次移动距离，否则在上一步就已经出现第 $1$ 类路径交叉的情况了。

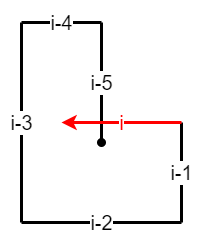
cross_3

第 $3$ 类，如上图所示，第 $i$ 次移动和第 $i-5$ 次移动（包含端点）交叉的情况，例如归纳中的 $6-2$ 和 $6-3$。

这种路径交叉需满足以下条件：

  • 第 $i-1$ 次移动距离大于等于第 $i-3$ 次移动距离减第 $i-5$ 次移动距离的差，且小于等于第 $i-3$ 次移动距离；注意此时第 $i-3$ 次移动距离一定大于第 $i-5$ 次移动距离，否则在两步之前就已经出现第 $1$ 类路径交叉的情况了。
  • 第 $i-2$ 次移动距离大于第 $i-4$ 次移动距离；注意此时第 $i-2$ 次移动距离一定不等于第 $i-4$ 次移动距离，否则在上一步就会出现第 $3$ 类路径交叉（或第 $2$ 类路径交叉）的情况了。
  • 第 $i$ 次移动距离大于等于第 $i-2$ 次移动距离减第 $i-4$ 次移动距离的差。

代码

[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution:
    def isSelfCrossing(self, distance: List[int]) -> bool:
        n = len(distance)
        for i in range(3, n):
            # 第 1 类路径交叉的情况
            if (distance[i] >= distance[i - 2]
                    and distance[i - 1] <= distance[i - 3]):
                return True

            # 第 2 类路径交叉的情况
            if i == 4 and (distance[3] == distance[1]
                           and distance[4] >= distance[2] - distance[0]):
                return True

            # 第 3 类路径交叉的情况
            if i >= 5 and (distance[i - 3] - distance[i - 5] <= distance[i - 1] <= distance[i - 3]
                           and distance[i] >= distance[i - 2] - distance[i - 4]
                           and distance[i - 2] > distance[i - 4]):
                return True
        return False
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public boolean isSelfCrossing(int[] distance) {
        int n = distance.length;
        for (int i = 3; i < n; ++i) {
            // 第 1 类路径交叉的情况
            if (distance[i] >= distance[i - 2] && distance[i - 1] <= distance[i - 3]) {
                return true;
            }

            // 第 2 类路径交叉的情况
            if (i == 4 && (distance[3] == distance[1]
                && distance[4] >= distance[2] - distance[0])) {
                return true;
            }

            // 第 3 类路径交叉的情况
            if (i >= 5 && (distance[i - 3] - distance[i - 5] <= distance[i - 1]
                && distance[i - 1] <= distance[i - 3]
                && distance[i] >= distance[i - 2] - distance[i - 4]
                && distance[i - 2] > distance[i - 4])) {
                return true;
            }
        }
        return false;
    }
}
[sol1-C#]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public class Solution {
    public bool IsSelfCrossing(int[] distance) {
        int n = distance.Length;
        for (int i = 3; i < n; ++i) {
            // 第 1 类路径交叉的情况
            if (distance[i] >= distance[i - 2] && distance[i - 1] <= distance[i - 3]) {
                return true;
            }

            // 第 2 类路径交叉的情况
            if (i == 4 && (distance[3] == distance[1]
                && distance[4] >= distance[2] - distance[0])) {
                return true;
            }

            // 第 3 类路径交叉的情况
            if (i >= 5 && (distance[i - 3] - distance[i - 5] <= distance[i - 1]
                && distance[i - 1] <= distance[i - 3]
                && distance[i] >= distance[i - 2] - distance[i - 4]
                && distance[i - 2] > distance[i - 4])) {
                return true;
            }
        }
        return false;
    }
}
[sol1-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
var isSelfCrossing = function(distance) {
    const n = distance.length;
    for (let i = 3; i < n; ++i) {
        // 第 1 类路径交叉的情况
        if (distance[i] >= distance[i - 2] && distance[i - 1] <= distance[i - 3]) {
            return true;
        }

        // 第 2 类路径交叉的情况
        if (i === 4 && (distance[3] === distance[1]
            && distance[4] >= distance[2] - distance[0])) {
            return true;
        }

        // 第 3 类路径交叉的情况
        if (i >= 5 && (distance[i - 3] - distance[i - 5] <= distance[i - 1]
            && distance[i - 1] <= distance[i - 3]
            && distance[i] >= distance[i - 2] - distance[i - 4]
            && distance[i - 2] > distance[i - 4])) {
            return true;
        }
    }
    return false;
};
[sol1-TypeScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
function isSelfCrossing(distance: number[]): boolean {
    const n: number = distance.length;
    for (let i = 3; i < n; ++i) {
        // 第 1 类路径交叉的情况
        if (distance[i] >= distance[i - 2] && distance[i - 1] <= distance[i - 3]) {
            return true;
        }

        // 第 2 类路径交叉的情况
        if (i === 4 && (distance[3] === distance[1]
            && distance[4] >= distance[2] - distance[0])) {
            return true;
        }

        // 第 3 类路径交叉的情况
        if (i >= 5 && (distance[i - 3] - distance[i - 5] <= distance[i - 1]
            && distance[i - 1] <= distance[i - 3]
            && distance[i] >= distance[i - 2] - distance[i - 4]
            && distance[i - 2] > distance[i - 4])) {
            return true;
        }
    }
    return false;
};
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
func isSelfCrossing(distance []int) bool {
    for i := 3; i < len(distance); i++ {
        // 第 1 类路径交叉的情况
        if distance[i] >= distance[i-2] && distance[i-1] <= distance[i-3] {
            return true
        }

        // 第 2 类路径交叉的情况
        if i == 4 && distance[3] == distance[1] &&
            distance[4] >= distance[2]-distance[0] {
            return true
        }

        // 第 3 类路径交叉的情况
        if i >= 5 && distance[i-3]-distance[i-5] <= distance[i-1] &&
            distance[i-1] <= distance[i-3] &&
            distance[i] >= distance[i-2]-distance[i-4] &&
            distance[i-2] > distance[i-4] {
            return true
        }
    }
    return false
}
[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    bool isSelfCrossing(vector<int>& distance) {
        int n = distance.size();
        for (int i = 3; i < n; ++i) {
            // 第 1 类路径交叉的情况
            if (distance[i] >= distance[i - 2] && distance[i - 1] <= distance[i - 3]) {
                return true;
            }

            // 第 2 类路径交叉的情况
            if (i == 4 && (distance[3] == distance[1]
                && distance[4] >= distance[2] - distance[0])) {
                return true;
            }

            // 第 3 类路径交叉的情况
            if (i >= 5 && (distance[i - 3] - distance[i - 5] <= distance[i - 1]
                && distance[i - 1] <= distance[i - 3]
                && distance[i] >= distance[i - 2] - distance[i - 4]
                && distance[i - 2] > distance[i - 4])) {
                return true;
            }
        }
        return false;
    }
};

复杂度分析

  • 时间复杂度：$O(n)$，其中 $n$ 为移动次数。

  • 空间复杂度：$O(1)$。

方法二：归纳法（归纳路径不交叉时的状态）

思路和算法

根据归纳结果，我们发现当不出现路径交叉时，只可能有以下三种情况：

  • 第 $1$ 种情况：对于每一次移动 $i$，第 $i$ 次移动距离都比第 $i-2$ 次移动距离更长，例如归纳中的 $3-3$、$4-9$、$5-8$ 和 $6-8$。
  • 第 $2$ 种情况：对于每一次移动 $i$，第 $i$ 次移动距离都比第 $i-2$ 次移动距离更短，即归纳中的 $3-1$ 具有的性质。
  • 第 $3$ 种情况：对于每一次移动 $i < j$，都满足第 $1$ 种情况；对于每一次移动 $i > j$，都满足第 $2$ 种情况。

具体地，对于第 $3$ 种情况的第 $j$ 次移动，有以下三种情况：

  • 第 $3.1$ 种情况：第 $j$ 次移动距离小于第 $j-2$ 次移动距离减去第 $j-4$ 次移动距离的差，例如归纳中的 $5-1$、$5-4$、$6-4$ 等。此时，第 $j+1$ 次移动距离需要小于第 $j-1$ 次移动距离才能不出现路径交叉。在边界条件下，这种情况会变为：第 $3$ 次移动距离小于第 $1$ 次移动距离，即归纳中的 $3-1$；第 $4$ 次移动距离小于第 $2$ 次移动距离，即归纳中的 $4-1$、$4-4$ 和 $4-7$。
  • 第 $3.2$ 种情况：第 $j$ 次移动距离大于等于第 $j-2$ 次移动距离减去第 $j-4$ 次移动距离的差，且小于等于第 $j-2$ 次移动距离，例如归纳中的 $5-5$、$5-6$、$5-7$ 等。此时，第 $j+1$ 次移动距离需要小于第 $j-1$ 次移动距离减去第 $j-3$ 次移动距离的差，才能不出现路径交叉。在边界条件下，这种情况会变为：第 $4$ 次的移动距离等于第 $2$ 次的移动距离且第 $3$ 次的移动距离大于第 $1$ 次的移动距离，即归纳中的 $4-8$。

代码

[sol2-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution:
    def isSelfCrossing(self, distance: List[int]) -> bool:
        n = len(distance)

        # 处理第 1 种情况
        i = 0
        while i < n and (i < 2 or distance[i] > distance[i - 2]):
            i += 1

        if i == n:
            return False

        # 处理第 j 次移动的情况
        if ((i == 3 and distance[i] == distance[i - 2])
                or (i >= 4 and distance[i] >= distance[i - 2] - distance[i - 4])):
            distance[i - 1] -= distance[i - 3]
        i += 1

        # 处理第 2 种情况
        while i < n and distance[i] < distance[i - 2]:
            i += 1

        return i != n
[sol2-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public boolean isSelfCrossing(int[] distance) {
        int n = distance.length;

        // 处理第 1 种情况
        int i = 0;
        while (i < n && (i < 2 || distance[i] > distance[i - 2])) {
            ++i;
        }

        if (i == n) {
            return false;
        }

        // 处理第 j 次移动的情况
        if ((i == 3 && distance[i] == distance[i - 2])
            || (i >= 4 && distance[i] >= distance[i - 2] - distance[i - 4])) {
            distance[i - 1] -= distance[i - 3];
        }
        ++i;

        // 处理第 2 种情况
        while (i < n && distance[i] < distance[i - 2]) {
            ++i;
        }

        return i != n;
    }
}
[sol2-C#]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public class Solution {
    public bool IsSelfCrossing(int[] distance) {
        int n = distance.Length;

        // 处理第 1 种情况
        int i = 0;
        while (i < n && (i < 2 || distance[i] > distance[i - 2])) {
            ++i;
        }

        if (i == n) {
            return false;
        }

        // 处理第 j 次移动的情况
        if ((i == 3 && distance[i] == distance[i - 2])
            || (i >= 4 && distance[i] >= distance[i - 2] - distance[i - 4])) {
            distance[i - 1] -= distance[i - 3];
        }
        ++i;

        // 处理第 2 种情况
        while (i < n && distance[i] < distance[i - 2]) {
            ++i;
        }

        return i != n;
    }
}
[sol2-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
var isSelfCrossing = function(distance) {
    const n = distance.length;

    // 处理第 1 种情况
    let i = 0;
    while (i < n && (i < 2 || distance[i] > distance[i - 2])) {
        ++i;
    }

    if (i === n) {
        return false;
    }

    // 处理第 j 次移动的情况
    if ((i === 3 && distance[i] == distance[i - 2])
        || (i >= 4 && distance[i] >= distance[i - 2] - distance[i - 4])) {
        distance[i - 1] -= distance[i - 3];
    }
    ++i;

    // 处理第 2 种情况
    while (i < n && distance[i] < distance[i - 2]) {
        ++i;
    }

    return i !== n;
};
[sol2-TypeScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
function isSelfCrossing(distance: number[]): boolean {
    const n: number = distance.length;

    // 处理第 1 种情况
    let i: number = 0;
    while (i < n && (i < 2 || distance[i] > distance[i - 2])) {
        ++i;
    }

    if (i === n) {
        return false;
    }

    // 处理第 j 次移动的情况
    if ((i === 3 && distance[i] == distance[i - 2])
        || (i >= 4 && distance[i] >= distance[i - 2] - distance[i - 4])) {
        distance[i - 1] -= distance[i - 3];
    }
    ++i;

    // 处理第 2 种情况
    while (i < n && distance[i] < distance[i - 2]) {
        ++i;
    }

    return i !== n;
};
[sol2-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
func isSelfCrossing(distance []int) bool {
    n := len(distance)

    // 处理第 1 种情况
    i := 0
    for i < n && (i < 2 || distance[i] > distance[i-2]) {
        i++
    }

    if i == n {
        return false
    }

    // 处理第 j 次移动的情况
    if i == 3 && distance[i] == distance[i-2] ||
        i >= 4 && distance[i] >= distance[i-2]-distance[i-4] {
        distance[i-1] -= distance[i-3]
    }
    i++

    // 处理第 2 种情况
    for i < n && distance[i] < distance[i-2] {
        i++
    }

    return i != n
}
[sol2-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    bool isSelfCrossing(vector<int>& distance) {
        int n = distance.size();

        // 处理第 1 种情况
        int i = 0;
        while (i < n && (i < 2 || distance[i] > distance[i - 2])) {
            ++i;
        }

        if (i == n) {
            return false;
        }

        // 处理第 j 次移动的情况
        if ((i == 3 && distance[i] == distance[i - 2])
            || (i >= 4 && distance[i] >= distance[i - 2] - distance[i - 4])) {
            distance[i - 1] -= distance[i - 3];
        }
        ++i;

        // 处理第 2 种情况
        while (i < n && distance[i] < distance[i - 2]) {
            ++i;
        }

        return i != n;
    }
};

复杂度分析

  • 时间复杂度：$O(n)$，其中 $n$ 为移动次数。

  • 空间复杂度：$O(1)$。

 Comments
On this page
0335-路径交叉