1035-不相交的线

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:25 2023-09-13 16:06:25 Updated    

在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足满足：

  • nums1[i] == nums2[j]
  • 且绘制的直线不与任何其他连线（非水平线）相交。

请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。

以这种方法绘制线条，并返回可以绘制的最大连线数。

示例 1：

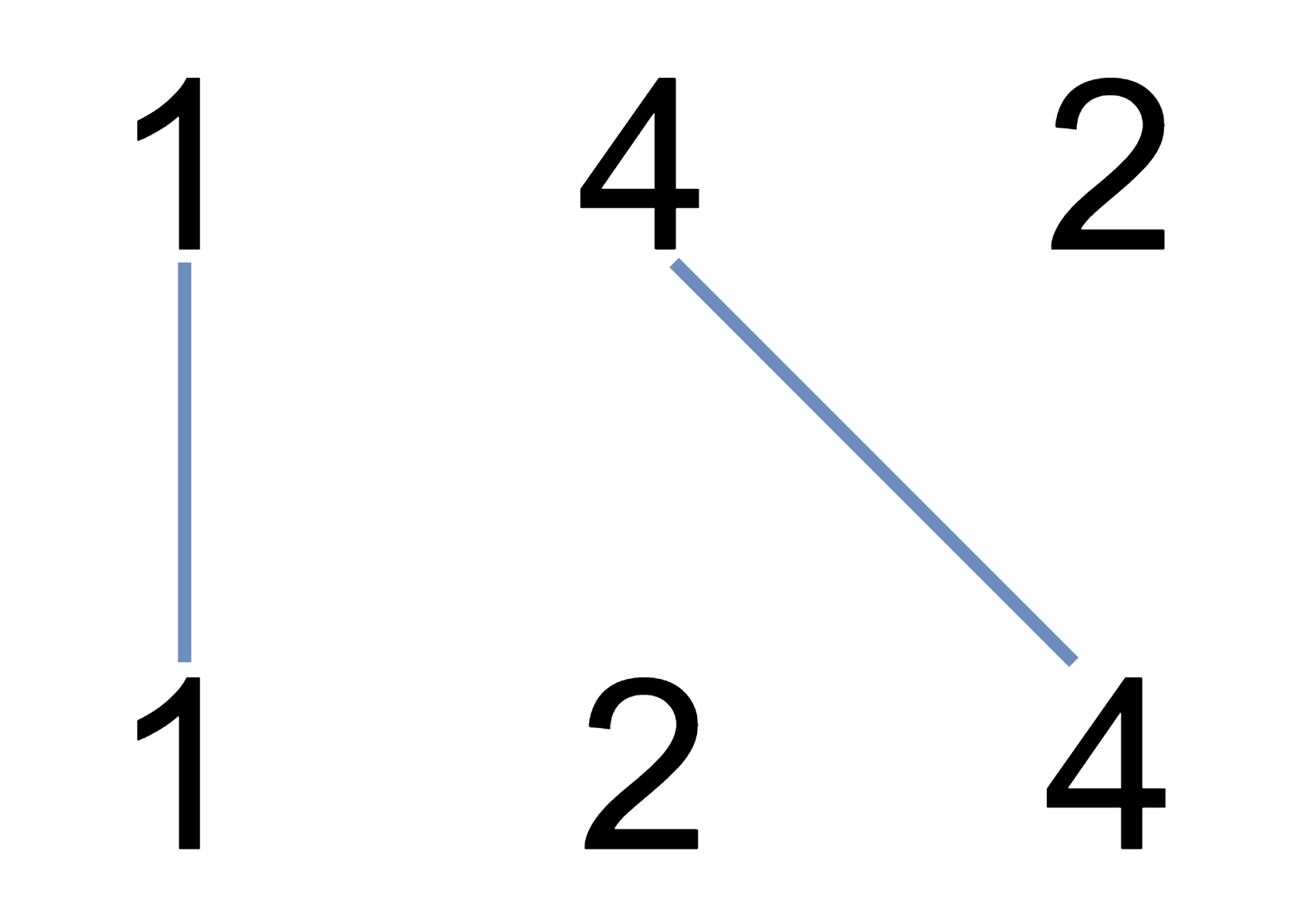
**输入：** nums1 = [1,4,2], nums2 = [1,2,4]
**输出：** 2
**解释：** 可以画出两条不交叉的线，如上图所示。 
但无法画出第三条不相交的直线，因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。

示例 2：

**输入：** nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
**输出：** 3

示例 3：

**输入：** nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
**输出：** 2

提示：

  • 1 <= nums1.length, nums2.length <= 500
  • 1 <= nums1[i], nums2[j] <= 2000

方法一：动态规划

给定两个数组 nums}_1 和 nums}_2，当 nums}_1[i]=\textit{nums}_2[j] 时，可以用一条直线连接 nums}_1[i] 和 nums}_2[j]。假设一共绘制了 k 条互不相交的直线，其中第 x 条直线连接 nums}_1[i_x] 和 nums}_2[j_x]，则对于任意 1 \le x \le k 都有 nums}_1[i_x]=\textit{nums}_2[j_x]，其中 i_1<i_2<\ldots<i_k，j_1<j_2<\ldots<j_k。

上述 k 条互不相交的直线分别连接了数组 nums}_1 和 nums}_2 的 k 对相等的元素，而且这 k 对相等的元素在两个数组中的相对顺序是一致的，因此，这 k 对相等的元素组成的序列即为数组 nums}_1 和 nums}_2 的公共子序列。要计算可以绘制的最大连线数，即为计算数组 nums}_1 和 nums}_2 的最长公共子序列的长度。最长公共子序列问题是典型的二维动态规划问题。

假设数组 nums}_1 和 nums}_2 的长度分别为 m 和 n，创建 m+1 行 n+1 列的二维数组 dp，其中 dp}[i][j] 表示 nums}_1[0:i] 和 nums}_2[0:j] 的最长公共子序列的长度。

上述表示中，nums}_1[0:i] 表示数组 nums}_1 的长度为 i 的前缀，nums}_2[0:j] 表示数组 nums}_2 的长度为 j 的前缀。

考虑动态规划的边界情况：

  • 当 i=0 时，nums}_1[0:i] 为空，空数组和任何数组的最长公共子序列的长度都是 0，因此对任意 0 \le j \le n，有 dp}[0][j]=0；

  • 当 j=0 时，nums}_2[0:j] 为空，同理可得，对任意 0 \le i \le m，有 dp}[i][0]=0。

因此动态规划的边界情况是：当 i=0 或 j=0 时，dp}[i][j]=0。

当 i>0 且 j>0 时，考虑 dp}[i][j] 的计算：

  • 当 nums}_1[i-1]=\textit{nums}_2[j-1] 时，将这两个相同的元素称为公共元素，考虑 nums}_1[0:i-1] 和 nums}_2[0:j-1] 的最长公共子序列，再增加一个元素（即公共元素）即可得到 nums}_1[0:i] 和 nums}_2[0:j] 的最长公共子序列，因此 dp}[i][j]=\textit{dp}[i-1][j-1]+1。

  • 当 nums}_1[i-1] \ne \textit{nums}_2[j-1] 时，考虑以下两项：

    • nums}_1[0:i-1] 和 nums}_2[0:j] 的最长公共子序列；

    • nums}_1[0:i] 和 nums}_2[0:j-1] 的最长公共子序列。

    要得到 nums}_1[0:i] 和 nums}_2[0:j] 的最长公共子序列，应取两项中的长度较大的一项，因此 dp}[i][j]=\max(\textit{dp}[i-1][j],\textit{dp}[i][j-1])。

由此可以得到如下状态转移方程：

\textit{dp}[i][j] = \begin{cases}
\textit{dp}[i-1][j-1]+1, & \textit{nums}_1[i-1]=\textit{nums}_2[j-1] \
\max(\textit{dp}[i-1][j],\textit{dp}[i][j-1]), & \textit{nums}_1[i-1] \ne \textit{nums}_2[j-1]
\end{cases}

最终计算得到 dp}[m][n] 即为数组 nums}_1 和 nums}_2 的最长公共子序列的长度，即可以绘制的最大连线数。

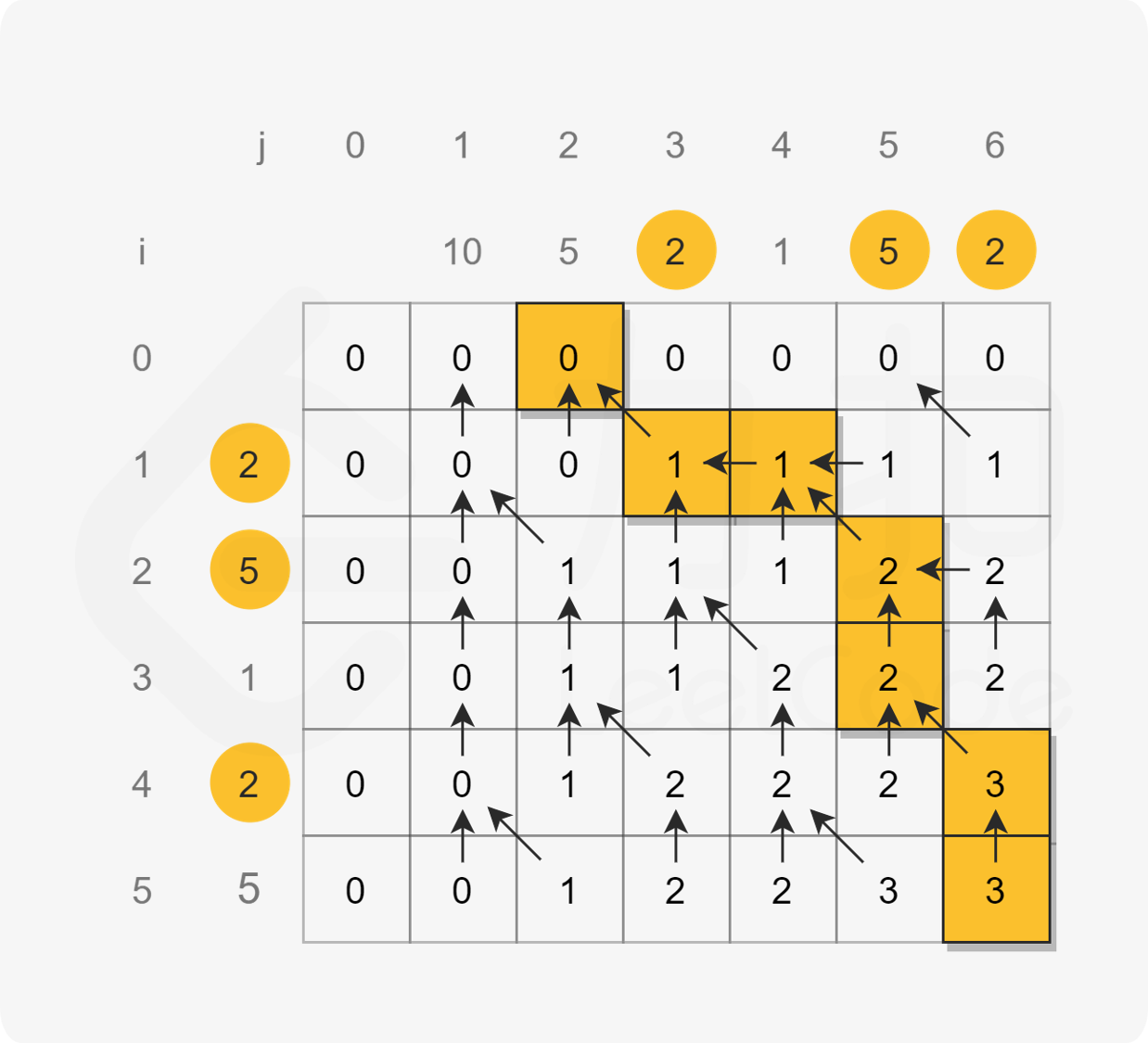fig1{:width=”80%”}

[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int m = nums1.length, n = nums2.length;
        int[][] dp = new int[m + 1][n + 1];
        for (int i = 1; i <= m; i++) {
            int num1 = nums1[i - 1];
            for (int j = 1; j <= n; j++) {
                int num2 = nums2[j - 1];
                if (num1 == num2) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[m][n];
    }
}
[sol1-C#]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public class Solution {
    public int MaxUncrossedLines(int[] nums1, int[] nums2) {
        int m = nums1.Length, n = nums2.Length;
        int[,] dp = new int[m + 1, n + 1];
        for (int i = 1; i <= m; i++) {
            int num1 = nums1[i - 1];
            for (int j = 1; j <= n; j++) {
                int num2 = nums2[j - 1];
                if (num1 == num2) {
                    dp[i, j] = dp[i - 1, j - 1] + 1;
                } else {
                    dp[i, j] = Math.Max(dp[i - 1, j], dp[i, j - 1]);
                }
            }
        }
        return dp[m, n];
    }
}
[sol1-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
var maxUncrossedLines = function(nums1, nums2) {
    const m = nums1.length, n = nums2.length;
    const dp = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0));
    for (let i = 1; i <= m; i++) {
        const num1 = nums1[i - 1];
        for (let j = 1; j <= n; j++) {
            const num2 = nums2[j - 1];
            if (num1 === num2) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    return dp[m][n];
};
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
func maxUncrossedLines(nums1, nums2 []int) int {
    m, n := len(nums1), len(nums2)
    dp := make([][]int, m+1)
    for i := range dp {
        dp[i] = make([]int, n+1)
    }
    for i, v := range nums1 {
        for j, w := range nums2 {
            if v == w {
                dp[i+1][j+1] = dp[i][j] + 1
            } else {
                dp[i+1][j+1] = max(dp[i][j+1], dp[i+1][j])
            }
        }
    }
    return dp[m][n]
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
    def maxUncrossedLines(self, nums1: List[int], nums2: List[int]) -> int:
        m, n = len(nums1), len(nums2)
        dp = [[0] * (n + 1) for _ in range(m + 1)]

        for i, num1 in enumerate(nums1):
            for j, num2 in enumerate(nums2):
                if num1 == num2:
                    dp[i + 1][j + 1] = dp[i][j] + 1
                else:
                    dp[i + 1][j + 1] = max(dp[i][j + 1], dp[i + 1][j])
        
        return dp[m][n]
[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        int m = nums1.size(), n = nums2.size();
        vector<vector<int>> dp(m + 1, vector<int>(n + 1));
        for (int i = 1; i <= m; i++) {
            int num1 = nums1[i - 1];
            for (int j = 1; j <= n; j++) {
                int num2 = nums2[j - 1];
                if (num1 == num2) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[m][n];
    }
};
[sol1-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int maxUncrossedLines(int* nums1, int nums1Size, int* nums2, int nums2Size) {
    int m = nums1Size, n = nums2Size;
    int dp[m + 1][n + 1];
    memset(dp, 0, sizeof(dp));
    for (int i = 1; i <= m; i++) {
        int num1 = nums1[i - 1];
        for (int j = 1; j <= n; j++) {
            int num2 = nums2[j - 1];
            if (num1 == num2) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else {
                dp[i][j] = fmax(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    return dp[m][n];
}

复杂度分析

  • 时间复杂度：O(mn)，其中 m 和 n 分别是数组 nums}_1 和 nums}_2 的长度。二维数组 dp 有 m+1 行和 n+1 列，需要对 dp 中的每个元素进行计算。

  • 空间复杂度：O(mn)，其中 m 和 n 分别是数组 nums}_1 和 nums}_2 的长度。创建了 m+1 行 n+1 列的二维数组 dp。

✨扣友帮帮团 - 互动答疑

讨论.jpg{:width=260px}

即日起 - 5 月 30 日，点击 这里  前往「扣友帮帮团 」活动页，把你遇到的问题大胆地提出来，让扣友为你解答～

🎁 奖励规则

被采纳数量排名 1～3 名：「力扣极客套装」 *1 并将获得「力扣神秘应援团」内测资格
被采纳数量排名 4～10 名：「力扣鼠标垫」 *1 并将获得「力扣神秘应援团」内测资格
「诲人不倦」：活动期间「解惑者」只要有 1 个回答被采纳，即可获得 20 LeetCoins 奖励！
「求知若渴」：活动期间「求知者」在活动页发起一次符合要求的疑问帖并至少采纳一次「解惑者」的回答，即可获得 20 LeetCoins 奖励！

活动详情猛戳链接了解更多：🐞 你有 BUG 我来帮 - 力扣互动答疑季

 Comments
On this page
1035-不相交的线
  1. ✨扣友帮帮团 - 互动答疑
    1. 🎁 奖励规则