1277-统计全为 1 的正方形子矩阵

给你一个 m * n 的矩阵，矩阵中的元素不是 0 就是 1，请你统计并返回其中完全由 1 组成的 正方形 子矩阵的个数。

示例 1：

**输入：** matrix =
[
  [0,1,1,1],
  [1,1,1,1],
  [0,1,1,1]
]
**输出：** 15
**解释：** 
边长为 1 的正方形有 **10** 个。
边长为 2 的正方形有 **4** 个。
边长为 3 的正方形有 **1** 个。
正方形的总数 = 10 + 4 + 1 = **15**.

示例 2：

**输入：** matrix = 
[
  [1,0,1],
  [1,1,0],
  [1,1,0]
]
**输出：** 7
**解释：**
边长为 1 的正方形有 **6** 个。 
边长为 2 的正方形有 **1** 个。
正方形的总数 = 6 + 1 = **7**.

提示：

• 1 <= arr.length <= 300
• 1 <= arr[0].length <= 300
• 0 <= arr[i][j] <= 1

方法一：递推

本题和 221. 最大正方形 非常类似，使用的方法也几乎相同。

我们用 f[i][j] 表示以 (i, j) 为右下角的正方形的最大边长，那么除此定义之外，f[i][j] = x 也表示以 (i, j) 为右下角的正方形的数目为 x（即边长为 1, 2, ..., x 的正方形各一个）。在计算出所有的 f[i][j] 后，我们将它们进行累加，就可以得到矩阵中正方形的数目。

我们尝试挖掘 f[i][j] 与相邻位置的关系来计算出 f[i][j] 的值。

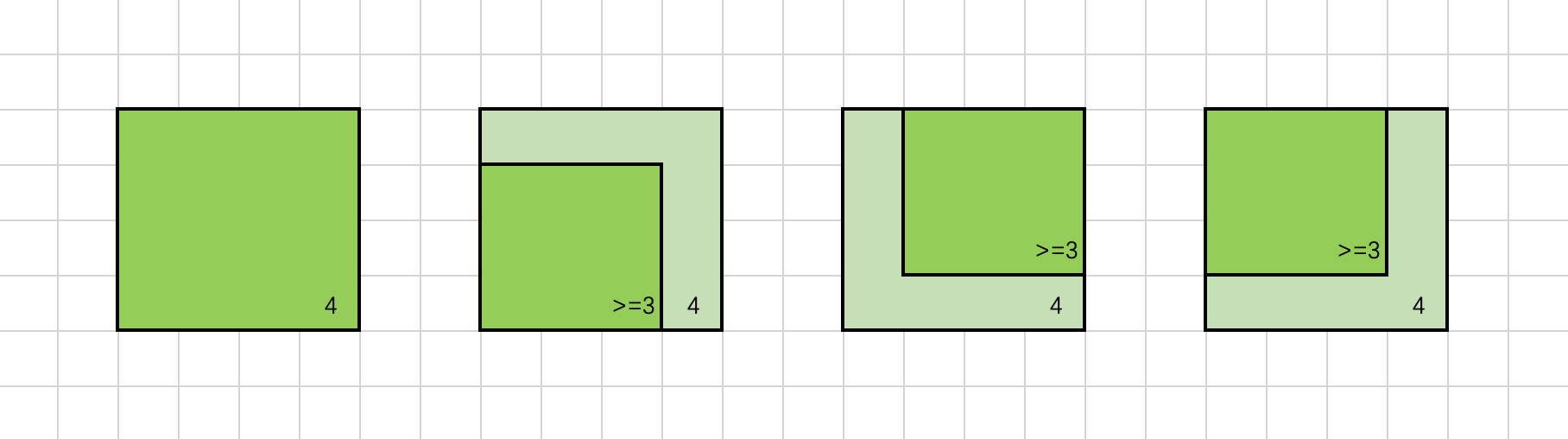{:width=600}

如上图所示，若对于位置 (i, j) 有 f[i][j] = 4，我们将以 (i, j) 为右下角、边长为 4 的正方形涂上色，可以发现其左侧位置 (i, j - 1)，上方位置 (i - 1, j) 和左上位置 (i - 1, j - 1) 均可以作为一个边长为 4 - 1 = 3 的正方形的右下角。也就是说，这些位置的的 f 值至少为 3，即：

f[i][j - 1] >= f[i][j] - 1
f[i - 1][j] >= f[i][j] - 1
f[i - 1][j - 1] >= f[i][j] - 1

将这三个不等式联立，可以得到：

\min\big(f[i][j - 1], f[i - 1][j], f[i - 1][j - 1]\big) \geq f[i][j] - 1

这是我们通过固定 f[i][j] 的值，判断其相邻位置与之的关系得到的不等式。同理，我们也可以固定 f[i][j] 相邻位置的值，得到另外的限制条件。

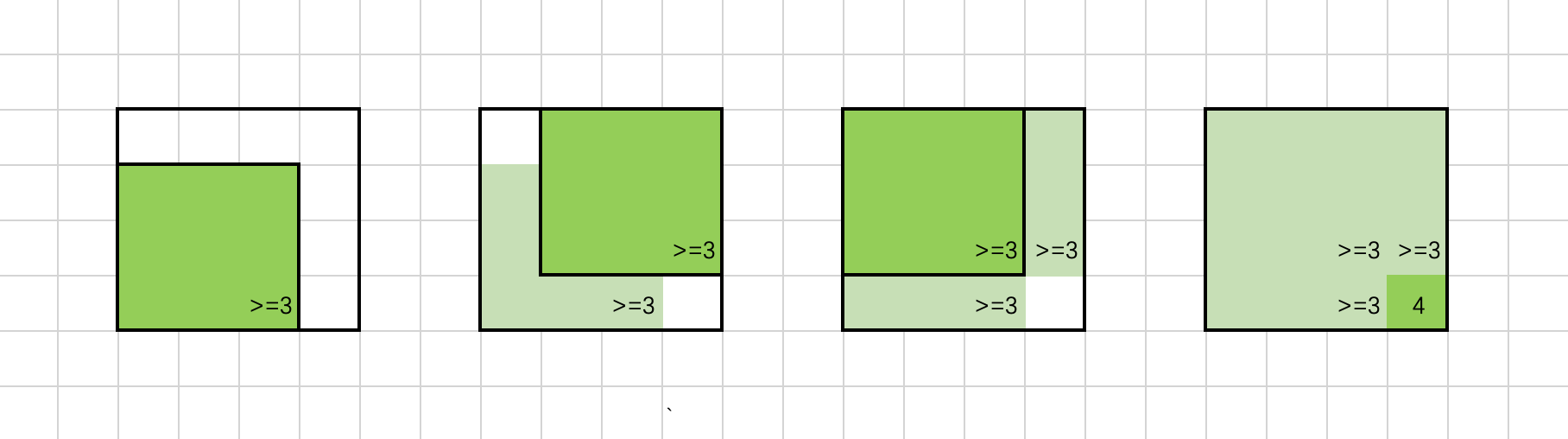{:width=600}

如上图所示，假设 f[i][j - 1]，f[i - 1][j] 和 f[i - 1][j - 1] 中的最小值为 3，也就是说，(i, j - 1)，(i - 1, j) 和 (i - 1, j - 1) 均可以作为一个边长为 3 的正方形的右下角。我们将这些边长为 3 的正方形依次涂上色，可以发现，如果位置 (i, j) 的元素为 1，那么它可以作为一个边长为 4 的正方形的右下角，f 值至少为 4，即：

f[i][j] \geq \min\big(f[i][j - 1], f[i - 1][j], f[i - 1][j - 1]\big) + 1

将其与上一个不等式联立，可以得到：

f[i][j] = \min\big(f[i][j - 1], f[i - 1][j], f[i - 1][j - 1]\big) + 1

这样我们就得到了 f[i][j] 的递推式。此外还要考虑边界（i = 0 或 j = 0）以及位置 (i, j) 的元素为 0 的情况，可以得到如下完整的递推式：

f[i][j] =
\begin{cases}
\text{matrix}[i][j] & ,\text{if} i == 0 \text{or} j == 0 \
0 & ,\text{if} \text{matrix[i][j]} == 0 \
\min\big(f[i][j - 1], f[i - 1][j], f[i - 1][j - 1]\big) + 1 & ,\text{otherwise}
\end{cases}

我们按照行优先的顺序依次计算 f[i][j] 的值，就可以得到最终的答案。

[sol1]

class Solution {
public:
    int countSquares(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        vector<vector<int>> f(m, vector<int>(n));
        int ans = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i == 0 || j == 0) {
                    f[i][j] = matrix[i][j];
                }
                else if (matrix[i][j] == 0) {
                    f[i][j] = 0;
                }
                else {
                    f[i][j] = min(min(f[i][j - 1], f[i - 1][j]), f[i - 1][j - 1]) + 1;
                }
                ans += f[i][j];
            }
        }
        return ans;
    }
};

[sol1]

class Solution:
    def countSquares(self, matrix: List[List[int]]) -> int:
        m, n = len(matrix), len(matrix[0])
        f = [[0] * n for _ in range(m)]
        ans = 0
        for i in range(m):
            for j in range(n):
                if i == 0 or j == 0:
                    f[i][j] = matrix[i][j]
                elif matrix[i][j] == 0:
                    f[i][j] = 0
                else:
                    f[i][j] = min(f[i][j - 1], f[i - 1][j], f[i - 1][j - 1]) + 1
                ans += f[i][j]
        return ans

复杂度分析

• 时间复杂度：O(MN)。

• 空间复杂度：O(MN)。由于递推式中 f[i][j] 只与本行和上一行的若干个值有关，因此空间复杂度可以优化至 O(N)。