1289-下降路径最小和 II

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:32 2023-09-13 16:06:32 Updated    

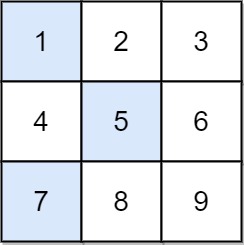
给你一个 n x n 整数矩阵 grid ，请你返回 非零偏移下降路径 数字和的最小值。

非零偏移下降路径 定义为：从 grid 数组中的每一行选择一个数字，且按顺序选出来的数字中，相邻数字不在原数组的同一列。

示例 1：

**输入：** grid = [[1,2,3],[4,5,6],[7,8,9]]
**输出：** 13
**解释：**
所有非零偏移下降路径包括：
[1,5,9], [1,5,7], [1,6,7], [1,6,8],
[2,4,8], [2,4,9], [2,6,7], [2,6,8],
[3,4,8], [3,4,9], [3,5,7], [3,5,9]
下降路径中数字和最小的是 [1,5,7] ，所以答案是 13 。

示例 2：

**输入：** grid = [[7]]
**输出：** 7

提示：

  • n == grid.length == grid[i].length
  • 1 <= n <= 200
  • -99 <= grid[i][j] <= 99

方法一：动态规划

思路与算法

我们可以使用动态规划来解决这个问题。

令状态 f[i][j] 表示从数组 grid 的前 i 行中的每一行选择一个数字，并且第 i 行选择的数字为 grid[i][j] 时，可以得到的路径和最小值。f[i][j] 可以从第 i - 1 行除了 f[i - 1][j] 之外的任意状态转移而来，因此有如下状态转移方程：

f[i][j] = \begin{cases}
\textit{grid}[0][j] & \text{if} \quad i = 0 \
\min(f[i-1][k]) + \textit{grid}[i][j] & \text{if} \quad i \ne 0, j \ne k
\end{cases}

最终，我们取第 n - 1 行中的最小值，即最小的 \min(f[n][j]) 作为答案。

代码

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int minFallingPathSum(vector<vector<int>>& grid) {
        int n = grid.size();
        vector<vector<int>> d(n, vector<int>(n, INT_MAX));
        for (int i = 0; i < n; i++) {
            d[0][i] = grid[0][i];
        }
        for (int i = 1; i < n; i++) {
            for (int j = 0; j < n; j++) {
                for (int k = 0; k < n; k++) {
                    if (j == k) {
                        continue;
                    }
                    d[i][j] = min(d[i][j], d[i - 1][k] + grid[i][j]);
                }
            }
        }
        int res = INT_MAX;
        for (int j = 0; j < n; j++) {
            res = min(res, d[n - 1][j]);
        }
        return res;
    }
};
[sol1-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
const int INF = 0x3f3f3f3f;

int minFallingPathSum(int** grid, int gridSize, int* gridColSize){
    int n = gridSize;
    int d[n][n];
    memset(d, 0x3f, sizeof(d));
    for (int i = 0; i < n; i++) {
        d[0][i] = grid[0][i];
    }
    for (int i = 1; i < n; i++) {
        for (int j = 0; j < n; j++) {
            for (int k = 0; k < n; k++) {
                if (j == k) {
                    continue;
                }
                d[i][j] = fmin(d[i][j], d[i - 1][k] + grid[i][j]);
            }
        }
    }
    int res = INT_MAX;
    for (int j = 0; j < n; j++) {
        res = fmin(res, d[n - 1][j]);
    }
    return res;
}
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int minFallingPathSum(int[][] grid) {
        int n = grid.length;
        int[][] d = new int[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                d[i][j] = Integer.MAX_VALUE;
            }
        }
        for (int i = 0; i < n; i++) {
            d[0][i] = grid[0][i];
        }
        for (int i = 1; i < n; i++) {
            for (int j = 0; j < n; j++) {
                for (int k = 0; k < n; k++) {
                    if (j == k) {
                        continue;
                    }
                    d[i][j] = Math.min(d[i][j], d[i - 1][k] + grid[i][j]);
                }
            }
        }
        int res = Integer.MAX_VALUE;
        for (int j = 0; j < n; j++) {
            res = Math.min(res, d[n - 1][j]);
        }
        return res;
    }
}
[sol1-C#]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public class Solution {
    public int MinFallingPathSum(int[][] grid) {
        int n = grid.Length;
        int[][] d = new int[n][];
        for (int i = 0; i < n; i++) {
            d[i] = new int[n];
            for (int j = 0; j < n; j++) {
                d[i][j] = int.MaxValue;
            }
        }
        for (int i = 0; i < n; i++) {
            d[0][i] = grid[0][i];
        }
        for (int i = 1; i < n; i++) {
            for (int j = 0; j < n; j++) {
                for (int k = 0; k < n; k++) {
                    if (j == k) {
                        continue;
                    }
                    d[i][j] = Math.Min(d[i][j], d[i - 1][k] + grid[i][j]);
                }
            }
        }
        int res = int.MaxValue;
        for (int j = 0; j < n; j++) {
            res = Math.Min(res, d[n - 1][j]);
        }
        return res;
    }
}
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
    def minFallingPathSum(self, grid: List[List[int]]) -> int:
        n = len(grid)
        d = [[10**9 for _ in range(n)] for _ in range(n)]
        for i in range(n):
            d[0][i] = grid[0][i]
        for i in range(n):
            for j in range(n):
                for k in range(n):
                    if j == k:
                        continue
                    d[i][j] = min(d[i][j], d[i - 1][k] + grid[i][j])
        return min(d[n - 1])
[sol1-Go]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
func minFallingPathSum(grid [][]int) int {
    n := len(grid)
    d := make([][]int, n)
    for i := 0; i < n; i++ {
        d[i] = make([]int, n)
        for j := 0; j < n; j++ {
            d[i][j] = math.MaxInt
        }
    }
    for i := 0; i < n; i++ {
        d[0][i] = grid[0][i]
    }
    for i := 1; i < n; i++ {
        for j := 0; j < n; j++ {
            for k := 0; k < n; k++ {
                if j == k {
                    continue
                }
                d[i][j] = min(d[i][j], d[i - 1][k] + grid[i][j])
            }
        }
    }
    res := math.MaxInt
    for i := 0; i < n; i++ {
        res = min(res, d[n - 1][i])
    }
    return res
}

func min(a int, b int) int {
    if a < b {
        return a
    }
    return b
}
[sol1-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
var minFallingPathSum = function(grid) {
    const n = grid.length;
    const d = new Array(n).fill(0).map(() => new Array(n).fill(Infinity));
    for (let i = 0; i < n; i++) {
        d[0][i] = grid[0][i];
    }
    for (let i = 1; i < n; i++) {
        for (let j = 0; j < n; j++) {
            for (let k = 0; k < n; k++) {
                if (j == k) {
                    continue;
                }
                d[i][j] = Math.min(d[i][j], d[i - 1][k] + grid[i][j]);
            }
        }
    }
    return Math.min(...d[n - 1]);
};

复杂度分析

  • 时间复杂度：O(n^3)，其中 n 是 grid 的行数和列数。我们使用三重循环来求解答案，每一层循环的复杂度为 O(n)，第 0 层单独求解和最终答案遍历的时间复杂度均为 O(n)，因此总的时间复杂度为 O(n^3)。

  • 空间复杂度：O(n^2)。我们使用二维数组 d[i][j] 来存储过程中的答案，实际上可以使用滚动数组优化至 O(n)。

方法二：转移过程优化

思路与算法

不难发现，求解第 i 行中所有的 f[i][j] 时，有很多状态在转移时所依赖的 \min(f[i-1][k]) 是相同的。我们令 first_min_sum 为第 i - 1 行状态中的最小值，first_min_index 为最小值对应的下标，second_min_sum 为状态次小值。那么有如下转移方程：

f[i][j] = \begin{cases}
\textit{grid}[0][j] & \text{if} \quad i = 0 \
\textit{first_min_sum} + grid[i][j] & \text{if} \quad i \ne 0, j \ne \textit{first_min_index} \
\textit{second_min_sum} + grid[i][j] & \text{if} \quad i \ne 0, j =\textit{first_min_index} \
\end{cases}

对于 i=0 的情况，我们不做变动。对于 i\ne 0 情况，判断当前遍历到的下标 j 是否与上一行状态中的最小值下标 first_min_index 相同，若相同，取次小值 second_min_sum 转移，若不同，取 first_min_sum 转移。

因此，我们只需维护第 i - 1 行相关的三个变量（最小值，最小值下标和次小值）就可以在 O(1) 时间内求解 f[i][j]。在求解 f[i][j] 的过程中，我们也只需记录第 i 行相关的变量即可，不用把所有的 f[i][j] 都保存下来。这样做可以将空间复杂度优化到 O(1)。

代码

[sol2-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    int minFallingPathSum(vector<vector<int>>& grid) {
        int n = grid.size();
        int first_min_sum = 0;
        int second_min_sum = 0;
        int first_min_index = -1;
        
        for (int i = 0; i < n; i++) {
            int cur_first_min_sum = INT_MAX;
            int cur_second_min_sum = INT_MAX;
            int cur_first_min_index = -1;
            
            for (int j = 0; j < n; j++) {
                int cur_sum = (j != first_min_index ? first_min_sum : second_min_sum) + grid[i][j];
                if (cur_sum < cur_first_min_sum) {
                    cur_second_min_sum = cur_first_min_sum;
                    cur_first_min_sum = cur_sum;
                    cur_first_min_index = j;
                } else if (cur_sum < cur_second_min_sum) {
                    cur_second_min_sum = cur_sum;
                }
            }
            first_min_sum = cur_first_min_sum;
            second_min_sum = cur_second_min_sum;
            first_min_index = cur_first_min_index;
        }
        return first_min_sum;
    }
};
[sol2-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
int minFallingPathSum(int** grid, int gridSize, int* gridColSize) {
    int first_min_sum = 0;
    int second_min_sum = 0;
    int first_min_index = -1;
    
    for (int i = 0; i < gridSize; i++) {
        int cur_first_min_sum = INT_MAX;
        int cur_second_min_sum = INT_MAX;
        int cur_first_min_index = -1;
        for (int j = 0; j < gridSize; j++) {
            int cur_sum = (j != first_min_index ? first_min_sum : second_min_sum) + grid[i][j];
            if (cur_sum < cur_first_min_sum) {
                cur_second_min_sum = cur_first_min_sum;
                cur_first_min_sum = cur_sum;
                cur_first_min_index = j;
            } else if (cur_sum < cur_second_min_sum) {
                cur_second_min_sum = cur_sum;
            }
        }
        first_min_sum = cur_first_min_sum;
        second_min_sum = cur_second_min_sum;
        first_min_index = cur_first_min_index;
    }
    return first_min_sum;
}
[sol2-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int minFallingPathSum(int[][] grid) {
        int n = grid.length;
        int first_min_sum = 0;
        int second_min_sum = 0;
        int first_min_index = -1;
        
        for (int i = 0; i < n; i++) {
            int cur_first_min_sum = Integer.MAX_VALUE;
            int cur_second_min_sum = Integer.MAX_VALUE;
            int cur_first_min_index = -1;
            
            for (int j = 0; j < n; j++) {
                int cur_sum = (j != first_min_index ? first_min_sum : second_min_sum) + grid[i][j];
                if (cur_sum < cur_first_min_sum) {
                    cur_second_min_sum = cur_first_min_sum;
                    cur_first_min_sum = cur_sum;
                    cur_first_min_index = j;
                } else if (cur_sum < cur_second_min_sum) {
                    cur_second_min_sum = cur_sum;
                }
            }
            first_min_sum = cur_first_min_sum;
            second_min_sum = cur_second_min_sum;
            first_min_index = cur_first_min_index;
        }
        return first_min_sum;
    }
}
[sol2-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution:
    def minFallingPathSum(self, grid: List[List[int]]) -> int:
        first_min_sum, second_min_sum = 0, 0
        first_min_index = -1
        for i in range(len(grid)):
            cur_first_min_sum, cur_second_min_sum = 10**9, 10**9
            cur_first_min_index = -1
            for j in range(len(grid)):
                cur_sum = grid[i][j]
                if j != first_min_index:
                    cur_sum += first_min_sum
                else:
                    cur_sum += second_min_sum
                if cur_sum < cur_first_min_sum:
                    cur_second_min_sum, cur_first_min_sum = cur_first_min_sum, cur_sum
                    cur_first_min_index = j
                elif cur_sum < cur_second_min_sum:
                    cur_second_min_sum = cur_sum
            first_min_sum, second_min_sum = cur_first_min_sum, cur_second_min_sum
            first_min_index = cur_first_min_index
        return first_min_sum
[sol2-Go]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
func minFallingPathSum(grid [][]int) int {
    n := len(grid)
    first_min_sum, second_min_sum := 0, 0
    first_min_index := -1
    
    for i := 0; i < n; i++ {
        cur_first_min_sum, cur_second_min_sum := math.MaxInt, math.MaxInt
        cur_first_min_index := -1
        
        for j := 0; j < n; j++ {
            cur_sum := grid[i][j]
            if j != first_min_index {
                cur_sum += first_min_sum
            } else {
                cur_sum += second_min_sum
            }
            if cur_sum < cur_first_min_sum {
                cur_second_min_sum, cur_first_min_sum = cur_first_min_sum, cur_sum
                cur_first_min_index = j
            } else if cur_sum < cur_second_min_sum {
                cur_second_min_sum = cur_sum
            }
        }
        first_min_sum, second_min_sum = cur_first_min_sum, cur_second_min_sum
        first_min_index = cur_first_min_index
    }
    return first_min_sum;
}
[sol2-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
var minFallingPathSum = function(grid) {
    const n = grid.length;
    let first_min_sum = 0, second_min_sum = 0;
    let first_min_index = -1;
    
    for (let i = 0; i < n; i++) {
        let cur_first_min_sum = Infinity, cur_second_min_sum = Infinity;
        let cur_first_min_index = -1;
        
        for (let j = 0; j < n; j++) {
            let cur_sum = grid[i][j];
            if (j != first_min_index) {
                cur_sum += first_min_sum;
            } else {
                cur_sum += second_min_sum;
            }
            if (cur_sum < cur_first_min_sum) {
                cur_second_min_sum = cur_first_min_sum;
                cur_first_min_sum = cur_sum;
                cur_first_min_index = j
            } else if (cur_sum < cur_second_min_sum) {
                cur_second_min_sum = cur_sum;
            }
        }
        first_min_sum = cur_first_min_sum;
        second_min_sum = cur_second_min_sum;
        first_min_index = cur_first_min_index;
    }
    return first_min_sum;
};

复杂度分析

  • 时间复杂度：O(n^2)，其中 n 是 grid 的行数和列数。

  • 空间复杂度：O(1)。过程中我们只使用了常数个变量。

 Comments
On this page
1289-下降路径最小和 II