1443-收集树上所有苹果的最少时间

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 11:03:24 2023-09-13 11:03:24 Updated    

给你一棵有 n 个节点的无向树，节点编号为 0 到 n-1 ，它们中有一些节点有苹果。通过树上的一条边，需要花费 1 秒钟。你从 **节点 0
**出发，请你返回最少需要多少秒，可以收集到所有苹果，并回到节点 0 。

无向树的边由 edges 给出，其中 edges[i] = [fromi, toi] ，表示有一条边连接 from 和 toi
。除此以外，还有一个布尔数组 hasApple ，其中 hasApple[i] = true 代表节点 i 有一个苹果，否则，节点 i
没有苹果。

示例 1：

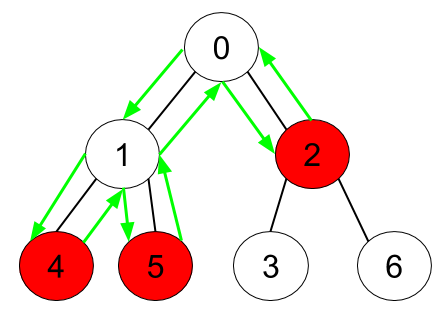
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/05/10/min_time_collect_apple_1.png)

**输入：** n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false]
**输出：** 8 
**解释：** 上图展示了给定的树，其中红色节点表示有苹果。一个能收集到所有苹果的最优方案由绿色箭头表示。

示例 2：

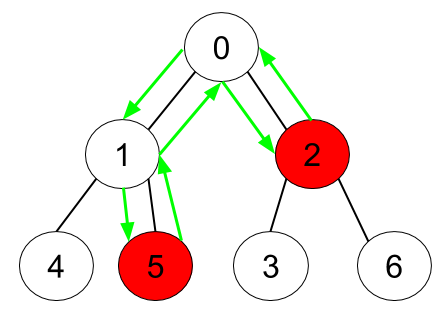
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/05/10/min_time_collect_apple_2.png)

**输入：** n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false]
**输出：** 6
**解释：** 上图展示了给定的树，其中红色节点表示有苹果。一个能收集到所有苹果的最优方案由绿色箭头表示。

示例 3：

**输入：** n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,false,false,false,false,false]
**输出：** 0

提示：

  • 1 <= n <= 10^5
  • edges.length == n - 1
  • edges[i].length == 2
  • 0 <= ai < bi <= n - 1
  • hasApple.length == n

解题思路

我们可以把一个树拆分成许多小子树来看，
对于一个根节点有三种情况

1.根节点无苹果，且其所有的子节点也都无苹果
那么走到该根节点的开销为0，就不用走这个根节点的分支(包括这个根节点)
2.根节点不管有没有苹果，只要其子节点当中有苹果
那么走到该根节点的开销为<1>走过所有有苹果的子节点所需要的开销 (继续调用dfs) + <2>上一步走到这个根节点的开销==2
3.根节点有苹果，且其子节点无苹果，或者说其子节点为空(该根节点为叶子节点)
那么走到该根节点的开销为上一步走到这个根节点的开销==2

三种情况可以简化为
走到该节点的开销curcost=所有孩子的开销childcost+走到该节点的开销(cost==2)
所有孩子的开销childcost可能=0，表示所有的子节点里都无苹果
1.假如所有孩子的开销childcost为0，且该节点本身就没有苹果，那么走到该节点的开销curcost=0
2.假如所有孩子开销!=0，不管该节点有没有苹果，走到该节点的开销curcost=childcost+2
3.假如所有孩子的开销childcost为0，但是该节点本身有苹果，那么走到该节点的开销curcost=0+2=2

这里解释一下为什么cost==2
除了0节点，在访问任意一个结点时，我们走到这个节点需要一步，回到上一个节点时还需要一步，相当于一条路来的时候走了一次
回去的时候走了一次，开销为2

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Solution {
public:

    //g 图
    //vis 判断节点是否被访问过,遍历过的节点不能再遍历，
    //同时因为是无向图，vis间接的确定了父子节点的关系，在子节点访问其子节点的时候不可能再去访问父节点
    //cost 只有以0节点刚进去的时候cost=0，在之后访问0节点的子节点时，cost都等于2(来回)

    int dfs(int curn, vector<vector<int> >& g, vector<bool>& vis, vector<bool>& hasApple, int cost)
    {
        if(vis[curn])
            return 0;
        vis[curn]=true;
        int childcost=0;
        for(auto next:g[curn])
        {
            childcost+=dfs(next,g,vis,hasApple,2);//遍历当前节点的所有子节点
            //如果childcost=0的话代表所有的子节点都没有苹果
        }

        //对应上面的情况1,所有子节点里都无苹果,且该节点本身也无苹果,走到该节点的开销=0
        if(!hasApple[curn] && childcost==0)
            return 0;

        //对应上面的情况2,3 走到该节点的开销为所有摘子节点里的苹果的开销+走到该节点的开销cost
        //如果childcost=0的话，对应情况3
        //如果childcost!=0的话，对应情况2
        return childcost+cost;
    }


    int minTime(int n, vector<vector<int>>& edges, vector<bool>& hasApple) {
        vector<vector<int> > g(n);
        vector<bool> vis(n,false);

        for(auto edge:edges)
        {
            g[edge[0]].push_back(edge[1]);
            g[edge[1]].push_back(edge[0]);
        }

        return dfs(0,g,vis,hasApple,0);//第一层由0节点出发，开销是0
    }

};

 Comments
On this page
1443-收集树上所有苹果的最少时间
  1. 解题思路
  2. 代码