1594-矩阵的最大非负积

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:31 2023-09-13 16:06:31 Updated    

给你一个大小为 m x n 的矩阵 grid 。最初，你位于左上角 (0, 0) ，每一步，你可以在矩阵中 向右 或 向下
移动。

在从左上角 (0, 0) 开始到右下角 (m - 1, n - 1) 结束的所有路径中，找出具有 最大非负积
的路径。路径的积是沿路径访问的单元格中所有整数的乘积。

返回 最大非负积 对 ** __109 + 7** 取余 的结果。如果最大积为 负数 ，则返回 __-1 。

注意， 取余是在得到最大积之后执行的。

示例 1：

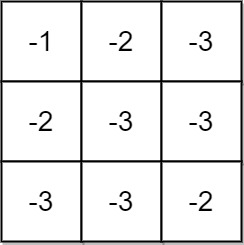
**输入：** grid = [[-1,-2,-3],[-2,-3,-3],[-3,-3,-2]]
**输出：** -1
**解释：** 从 (0, 0) 到 (2, 2) 的路径中无法得到非负积，所以返回 -1 。

示例 2：

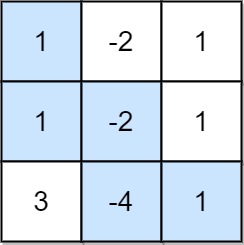
**输入：** grid = [[1,-2,1],[1,-2,1],[3,-4,1]]
**输出：** 8
**解释：** 最大非负积对应的路径如图所示 (1 * 1 * -2 * -4 * 1 = 8)

示例 3：

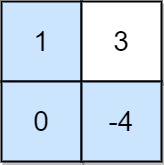
**输入：** grid = [[1,3],[0,-4]]
**输出：** 0
**解释：** 最大非负积对应的路径如图所示 (1 * 0 * -4 = 0)

提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 15
  • -4 <= grid[i][j] <= 4

方法一：动态规划

思路与算法

由于矩阵中的元素有正有负，要想得到最大积，我们只存储移动过程中的最大积是不够的，例如当前的最大积为正数时，乘上一个负数后，反而不如一个负数乘上相同的负数得到的积大。

因此，我们需要存储的是移动过程中的积的范围，也就是积的最小值以及最大值。由于只能向下或者向右走，我们可以考虑使用动态规划的方法解决本题。

设 maxgt}[i][j], \textit{minlt}[i][j] 分别为从坐标 (0, 0) 出发，到达位置 (i, j) 时乘积的最大值与最小值。由于我们只能向下或者向右走，因此乘积的取值必然只与 (i, j-1) 和 (i-1, j) 两个位置有关。

对于乘积的最大值而言：若 grid}[i][j] \ge 0，则 maxgt}[i][j] 的取值取决于这两个位置的最大值，此时

\textit{maxgt}[i][j] = \max(\textit{maxgt}[i][j-1], \textit{maxgt}[i-1][j]) \times \textit{grid}[i][j]

相反地，若 grid}[i][j] \le 0，则 maxgt}[i][j] 的取值取决于这两个位置的最小值，此时

\textit{maxgt}[i][j] = \min(\textit{minlt}[i][j-1], \textit{minlt}[i-1][j]) \times \textit{grid}[i][j]

计算乘积的最小值也是类似的思路。若 grid}[i][j] \ge 0，此时

\textit{mingt}[i][j] = \min(\textit{mingt}[i][j-1], \textit{mingt}[i-1][j]) \times \textit{grid}[i][j]

若 grid}[i][j] \le 0，此时

\textit{mingt}[i][j] = \max(\textit{maxgt}[i][j-1], \textit{maxgt}[i-1][j]) \times \textit{grid}[i][j]

特别地，当 i=0 时，只需要从 (i, j-1) 进行转移；j=0 时，只需要从 (i-1, j) 进行转移；i=0 且 j=0 时，maxgt}[i][j] 与 mingt}[i][j] 的值均为左上角的元素值 grid}[i][j]。

最终的答案即为 maxgt}[m-1][n-1]，其中 m 和 n 分别是矩阵的行数与列数。

代码

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    int maxProductPath(vector<vector<int>>& grid) {
        const int mod = 1000000000 + 7;
        int m = grid.size(), n = grid[0].size();
        vector<vector<long long>> maxgt(m, vector<long long>(n));
        vector<vector<long long>> minlt(m, vector<long long>(n));

        maxgt[0][0] = minlt[0][0] = grid[0][0];
        for (int i = 1; i < n; i++) {
            maxgt[0][i] = minlt[0][i] = maxgt[0][i - 1] * grid[0][i];
        }
        for (int i = 1; i < m; i++) {
            maxgt[i][0] = minlt[i][0] = maxgt[i - 1][0] * grid[i][0];
        }

        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (grid[i][j] >= 0) {
                    maxgt[i][j] = max(maxgt[i][j - 1], maxgt[i - 1][j]) * grid[i][j];
                    minlt[i][j] = min(minlt[i][j - 1], minlt[i - 1][j]) * grid[i][j];
                } else {
                    maxgt[i][j] = min(minlt[i][j - 1], minlt[i - 1][j]) * grid[i][j];
                    minlt[i][j] = max(maxgt[i][j - 1], maxgt[i - 1][j]) * grid[i][j];
                }
            }
        }
        if (maxgt[m - 1][n - 1] < 0) {
            return -1;
        } else {
            return maxgt[m - 1][n - 1] % mod;
        }
    }
};
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
    public int maxProductPath(int[][] grid) {
        final int MOD = 1000000000 + 7;
        int m = grid.length, n = grid[0].length;
        long[][] maxgt = new long[m][n];
        long[][] minlt = new long[m][n];

        maxgt[0][0] = minlt[0][0] = grid[0][0];
        for (int i = 1; i < n; i++) {
            maxgt[0][i] = minlt[0][i] = maxgt[0][i - 1] * grid[0][i];
        }
        for (int i = 1; i < m; i++) {
            maxgt[i][0] = minlt[i][0] = maxgt[i - 1][0] * grid[i][0];
        }

        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (grid[i][j] >= 0) {
                    maxgt[i][j] = Math.max(maxgt[i][j - 1], maxgt[i - 1][j]) * grid[i][j];
                    minlt[i][j] = Math.min(minlt[i][j - 1], minlt[i - 1][j]) * grid[i][j];
                } else {
                    maxgt[i][j] = Math.min(minlt[i][j - 1], minlt[i - 1][j]) * grid[i][j];
                    minlt[i][j] = Math.max(maxgt[i][j - 1], maxgt[i - 1][j]) * grid[i][j];
                }
            }
        }
        if (maxgt[m - 1][n - 1] < 0) {
            return -1;
        } else {
            return (int) (maxgt[m - 1][n - 1] % MOD);
        }
    }
}
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution:
    def maxProductPath(self, grid: List[List[int]]) -> int:
        mod = 10**9 + 7
        m, n = len(grid), len(grid[0])
        maxgt = [[0] * n for _ in range(m)]
        minlt = [[0] * n for _ in range(m)]

        maxgt[0][0] = minlt[0][0] = grid[0][0]
        for i in range(1, n):
            maxgt[0][i] = minlt[0][i] = maxgt[0][i - 1] * grid[0][i]
        for i in range(1, m):
            maxgt[i][0] = minlt[i][0] = maxgt[i - 1][0] * grid[i][0]
        
        for i in range(1, m):
            for j in range(1, n):
                if grid[i][j] >= 0:
                    maxgt[i][j] = max(maxgt[i][j - 1], maxgt[i - 1][j]) * grid[i][j]
                    minlt[i][j] = min(minlt[i][j - 1], minlt[i - 1][j]) * grid[i][j]
                else:
                    maxgt[i][j] = min(minlt[i][j - 1], minlt[i - 1][j]) * grid[i][j]
                    minlt[i][j] = max(maxgt[i][j - 1], maxgt[i - 1][j]) * grid[i][j]
        
        if maxgt[m - 1][n - 1] < 0:
            return -1
        return maxgt[m - 1][n - 1] % mod

复杂度分析

  • 时间复杂度：O(mn)，其中 m 和 n 为矩阵的行数与列数。我们需要遍历矩阵的每一个元素，而处理每个元素时只需要常数时间。

  • 空间复杂度：O(mn)。我们开辟了两个与原矩阵等大的数组。

 Comments
On this page
1594-矩阵的最大非负积