1976-到达目的地的方案数

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:29 2023-09-13 16:06:29 Updated    

你在一个城市里，城市由 n 个路口组成，路口编号为 0 到 n - 1 ，某些路口之间有 双向
道路。输入保证你可以从任意路口出发到达其他任意路口，且任意两个路口之间最多有一条路。

给你一个整数 n 和二维整数数组 roads ，其中 roads[i] = [ui, vi, timei] 表示在路口 ui 和 vi
之间有一条需要花费 timei 时间才能通过的道路。你想知道花费 最少时间 从路口 0 出发到达路口 n - 1 的方案数。

请返回花费 最少时间 到达目的地的 路径数目 。由于答案可能很大，将结果对 109 + 7 取余 后返回。

示例 1：

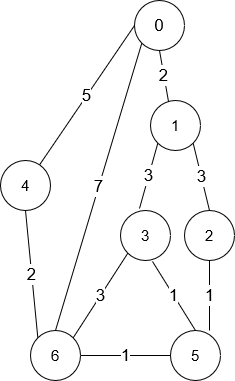
**输入：** n = 7, roads = [[0,6,7],[0,1,2],[1,2,3],[1,3,3],[6,3,3],[3,5,1],[6,5,1],[2,5,1],[0,4,5],[4,6,2]]
**输出：** 4
**解释：** 从路口 0 出发到路口 6 花费的最少时间是 7 分钟。
四条花费 7 分钟的路径分别为：
- 0 ➝ 6
- 0 ➝ 4 ➝ 6
- 0 ➝ 1 ➝ 2 ➝ 5 ➝ 6
- 0 ➝ 1 ➝ 3 ➝ 5 ➝ 6

示例 2：

**输入：** n = 2, roads = [[1,0,10]]
**输出：** 1
**解释：** 只有一条从路口 0 到路口 1 的路，花费 10 分钟。

提示：

  • 1 <= n <= 200
  • n - 1 <= roads.length <= n * (n - 1) / 2
  • roads[i].length == 3
  • 0 <= ui, vi <= n - 1
  • 1 <= timei <= 109
  • ui != vi
  • 任意两个路口之间至多有一条路。
  • 从任意路口出发，你能够到达其他任意路口。

方法一：最短路 + 有向无环图上的动态规划

提示 1

记 dist}[i] 表示从起点 0 到节点 i 的最短路径的长度。

如果我们希望花费最短的时间从起点 0 到达终点 n-1，那么我们走过的每一条边 u \to v 都需要满足：

\textit{dist}[v] - \textit{dist}[u] = \textit{length}(u \to v)

其中 length}(u \to v) 表示连接 u 与 v 的这条边的长度。

提示 1 解释

假设我们当前位于节点 u。要想走出从起点 0 经过节点 u 到达终点 n-1 的最短路径，我们首先一定要在最短的时间内到达节点 u，也就是 dist}[u]。

那么我们如何选择下一个节点呢？假设某一节点 v 与节点 u 相邻，即存在一条 u \to v 的边。经过这条边后，我们花费的时间变为 dist}[u] + \textit{length}(u \to v)，那么与 dist}[v] 本身对比，会有下面的几种情况：

  • 如果 dist}[u] + \textit{length}(u \to v) < \textit{dist}[v]，那这是不可能的。因为 dist}[v] 表示从起点 0 到节点 v 的最短路径长度，这就与我们求出的答案相矛盾了。

  • 如果 dist}[u] + \textit{length}(u \to v) = \textit{dist}[v]，那么我们在最短的时间内到达了节点 v，即目前我们还是有可能在最短的时间内到达终点 n-1 的。

  • 如果 dist}[u] + \textit{length}(u \to v) > \textit{dist}[v]，难么我们就没有机会在最短的时间内（在经过节点 v 的前提下）到达终点 n-1 了。

提示 2

我们对于给定的城市路线的「无向图」建立一个新的「有向图」G：

  • 「无向图」与「有向图」的节点相同；

  • 「有向图」中有一条 u \to v 的有向边，当且仅当 dist}[v] - \textit{dist}[u] = \textit{length}(u \to v) 成立。

可以发现 G 一定是一个无环图，因为每一条有向边总是从 dist 值较小的节点指向 dist 值较大的节点，因此图 G 中不可能存在环。

这样一来，我们在图 G 上从起点 0 开始，顺便边的方法任意地进行移动，只要到达终点 n-1，就一定是一条最短路径。我们就可以使用动态规划的方法，求出从起点 0 到终点 n-1 的路径数目了。

思路与算法

记 f[i] 表示在图 G 上从节点 i 走到终点 n-1 的路径数目。在进行动态规划时，我们可以考虑下一个走到的节点 j，那么有：

f[i] = \sum_{(i \to j) \in G} f[j]

特别地，当 i=n-1 时，我们已经到达了终点，那么有：

f[i] = 1

最终的答案即为 f[0]。

细节

上述的状态转移方程使用自顶向下的记忆化搜索编写起来较为容易。本质上来说，在有向无环图上的动态规划的求解顺序可以为该图的任意一种拓扑排序（或者拓扑排序的逆序）。「记忆化搜索」对应着「深度优先搜索」求解拓扑排序，而「动态规划」对应着「广度优先搜索」求解拓扑排序。

dist 的值可以通过任一最短路径算法求得。在本题中，节点个数不超过 200，因此可以使用 Floyd 算法在 O(n^3) 的时间内求出 dist。当然，我们也可以使用 Dijkstra 算法在 O(n^2) 的时间内求出 dist。

代码

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
class Solution {
private:
    static constexpr int mod = 1000000007;

public:
    int countPaths(int n, vector<vector<int>>& roads) {
        vector<vector<long long>> dist(n, vector<long long>(n, LLONG_MAX / 2));
        for (int i = 0; i < n; ++i) {
            dist[i][i] = 0;
        }
        for (auto&& road: roads) {
            int x = road[0], y = road[1], z = road[2];
            dist[x][y] = dist[y][x] = z;
        }

        // Floyd 算法求解最短路
        // 完成后，dist[0][i] 即为正文部分的 dist[i]
        // for (int k = 0; k < n; ++k) {
        //     for (int i = 0; i < n; ++i) {
        //         for (int j = 0; j < n; ++j) {
        //             dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
        //         }
        //     }
        // }

        // Dijkstra 算法求解最短路
        // 完成后，dist[0][i] 即为正文部分的 dist[i]
        vector<int> used(n);
        for (int _ = 0; _ < n; ++_) {
            int u = -1;
            for (int i = 0; i < n; ++i) {
                if (!used[i] && (u == -1 || dist[0][i] < dist[0][u])) {
                    u = i;
                }
            }
            used[u] = true;
            for (int i = 0; i < n; ++i) {
                dist[0][i] = min(dist[0][i], dist[0][u] + dist[u][i]);
            }
        }

        // 构造图 G
        vector<vector<int>> g(n);
        for (auto&& road: roads) {
            int x = road[0], y = road[1], z = road[2];
            if (dist[0][y] - dist[0][x] == z) {
                g[x].push_back(y);
            }
            else if (dist[0][x] - dist[0][y] == z) {
                g[y].push_back(x);
            }
        }

        vector<int> f(n, -1);
        function<int(int)> dfs = [&](int u) {
            if (u == n - 1) {
                return 1;
            }
            if (f[u] != -1) {
                return f[u];
            }

            f[u] = 0;
            for (int v: g[u]) {
                f[u] += dfs(v);
                if (f[u] >= mod) {
                    f[u] -= mod;
                }
            }
            return f[u];
        };
        return dfs(0);
    }
};
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class Solution:
    def countPaths(self, n: int, roads: List[List[int]]) -> int:
        mod = 10**9 + 7
        
        dist = [[float("inf")] * n for _ in range(n)]
        for i in range(n):
            dist[i][i] = 0
        
        for x, y, z in roads:
            dist[x][y] = dist[y][x] = z
        
        # Floyd 算法求解最短路
        # 完成后，dist[0][i] 即为正文部分的 dist[i]
        # for k in range(n):
        #     for i in range(n):
        #         for j in range(n):
        #             dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])

        # Dijkstra 算法求解最短路
        # 完成后，dist[0][i] 即为正文部分的 dist[i]
        seen = set()
        for _ in range(n - 1):
            u = None
            for i in range(n):
                if i not in seen and (not u or dist[0][i] < dist[0][u]):
                    u = i
            seen.add(u)
            for i in range(n):
                dist[0][i] = min(dist[0][i], dist[0][u] + dist[u][i])

        # 构造图 G
        g = defaultdict(list)
        for x, y, z in roads:
            if dist[0][y] - dist[0][x] == z:
                g[x].append(y)
            elif dist[0][x] - dist[0][y] == z:
                g[y].append(x)

        @cache
        def dfs(u: int) -> int:
            if u == n - 1:
                return 1

            ret = 0
            for v in g[u]:
                ret += dfs(v)
            return ret % mod
        
        ans = dfs(0)
        dfs.cache_clear()
        return ans

复杂度分析

  • 时间复杂度：O(n^3) 或 O(n^2)。由于动态规划需要的时间为 O(n^2)，因此算法的瓶颈在于求解 dist。如果使用 Floyd 算法，那么时间复杂度为 O(n^3)；如果使用 Dijkstra 算法，那么时间复杂度为 O(n^2)。

  • 空间复杂度：O(n^2)。在使用 Floyd 算法时，我们需要将图以邻接矩阵的形式进行存储，因此需要 O(n^2) 的空间。而对于 Dijkstra 算法而言，使用的空间正比于图中的边数，而本题的数据范围中的边数最多为 \dfrac{n(n-1)}{2} = O(n^2)，因此同样需要 O(n^2) 的空间。

 Comments
On this page
1976-到达目的地的方案数