1993-树上的操作

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:30 2023-09-13 16:06:30 Updated    

给你一棵 n 个节点的树，编号从 0 到 n - 1 ，以父节点数组 parent 的形式给出，其中 parent[i] 是第 i
个节点的父节点。树的根节点为 0 号节点，所以 parent[0] = -1
，因为它没有父节点。你想要设计一个数据结构实现树里面对节点的加锁，解锁和升级操作。

数据结构需要支持如下函数：

  • Lock： 指定用户给指定节点 上锁 ，上锁后其他用户将无法给同一节点上锁。只有当节点处于未上锁的状态下，才能进行上锁操作。
  • Unlock： 指定用户给指定节点 解锁 ，只有当指定节点当前正被指定用户锁住时，才能执行该解锁操作。
  • Upgrade： 指定用户给指定节点 上锁 ，并且将该节点的所有子孙节点 解锁 。只有如下 3 个条件 全部 满足时才能执行升级操作：
    • 指定节点当前状态为未上锁。
    • 指定节点至少有一个上锁状态的子孙节点（可以是 任意 用户上锁的）。
    • 指定节点没有任何上锁的祖先节点。

请你实现 LockingTree 类：

  • LockingTree(int[] parent) 用父节点数组初始化数据结构。
  • lock(int num, int user) 如果 id 为 user 的用户可以给节点 num 上锁，那么返回 true ，否则返回 false 。如果可以执行此操作，节点 num 会被 id 为 user 的用户 上锁 。
  • unlock(int num, int user) 如果 id 为 user 的用户可以给节点 num 解锁，那么返回 true ，否则返回 false 。如果可以执行此操作，节点 num 变为 未上锁 状态。
  • upgrade(int num, int user) 如果 id 为 user 的用户可以给节点 num 升级，那么返回 true ，否则返回 false 。如果可以执行此操作，节点 num 会被 升级 。

示例 1：

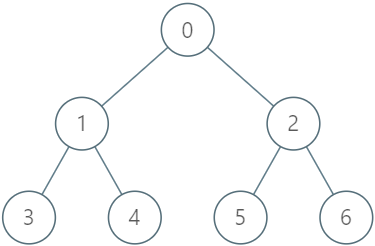
**输入：**
["LockingTree", "lock", "unlock", "unlock", "lock", "upgrade", "lock"]
[[[-1, 0, 0, 1, 1, 2, 2]], [2, 2], [2, 3], [2, 2], [4, 5], [0, 1], [0, 1]]
**输出：**
[null, true, false, true, true, true, false]

**解释：**
LockingTree lockingTree = new LockingTree([-1, 0, 0, 1, 1, 2, 2]);
lockingTree.lock(2, 2);    // 返回 true ，因为节点 2 未上锁。
                           // 节点 2 被用户 2 上锁。
lockingTree.unlock(2, 3);  // 返回 false ，因为用户 3 无法解锁被用户 2 上锁的节点。
lockingTree.unlock(2, 2);  // 返回 true ，因为节点 2 之前被用户 2 上锁。
                           // 节点 2 现在变为未上锁状态。
lockingTree.lock(4, 5);    // 返回 true ，因为节点 4 未上锁。
                           // 节点 4 被用户 5 上锁。
lockingTree.upgrade(0, 1); // 返回 true ，因为节点 0 未上锁且至少有一个被上锁的子孙节点（节点 4）。
                           // 节点 0 被用户 1 上锁，节点 4 变为未上锁。
lockingTree.lock(0, 1);    // 返回 false ，因为节点 0 已经被上锁了。

提示：

  • n == parent.length
  • 2 <= n <= 2000
  • 对于 i != 0 ，满足 0 <= parent[i] <= n - 1
  • parent[0] == -1
  • 0 <= num <= n - 1
  • 1 <= user <= 104
  • parent 表示一棵合法的树。
  • lock ，unlock 和 upgrade 的调用 **总共 **不超过 2000 次。

简单介绍一下需要的知识点：

  1. 从根开始DFS遍历树可以得到DFS序列（先序遍历），每个节点的子树对应序列中的以该节点开始，长度为子树大小的区间。
  2. 树状数组可以分别在对数时间做到：区间加，单点询问；单点加，区间求和，求出前缀和大于等于某个值的最小下标。

维护2个树状数组up和down，加锁时：

  1. 在up中给该节点子树区间+1。
  2. 在down中给该节点+1.

考虑upgrade操作：

  1. 从该节点到根都不能有锁。这等价于up中该节点的值为0.
  2. 子树中有锁，首先区间和不为0，可以通过树状数组上二分逐个求出子树中的锁。每找到一个锁需要对数时间，这部分的复杂度依赖于lock操作的次数，因此均摊是对数时间的。

参考代码：

[]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
struct BIT : vector<int>{
    BIT(int n = 0): vector<int>(n){}
    void add(int p, int x) {
        for (; p < (int)size(); p += p &- p) at(p) += x;
    }
    int sum(int p) {
        int res = 0;
        for (; p; p -= p & -p) res += at(p);
        return res;
    }
    int query(int x) {
        //find the smallest positive integer p such that sum(p) >= x
        int L = 0, R = size();
        while (L + 1 < R) {
            int m = (L + R) >> 1;
            if (at(m) < x) {
                x -= at(m);
                L = m;
            }
            else R = m;
        }
        return R;
    }
};
class LockingTree {
public:
    vector<int> size, p, q, mark;
    BIT down, up;
    LockingTree(vector<int>& parent): size(parent.size()), p(parent.size()), q(parent.size() + 1), mark(parent.size(), -1), up(parent.size() + 1){ 
        vector<vector<int>> children(parent.size());
        for (int i = 1; i < (int)parent.size(); i += 1) children[parent[i]].push_back(i);
        int timer = 0;
        function<void(int)> dfs = [&](int u) {
            size[u] = 1;
            p[u] = timer += 1;
            q[timer] = u;
            for (int v : children[u]) {
                dfs(v);
                size[u] += size[v];
            }
        };
        dfs(0);
        int k = 1;
        while (k <= (int)parent.size()) k <<= 1;
        down.resize(k);
    }
    bool lock(int num, int user) {
        if (mark[num] != -1) return false;
        mark[num] = user;
        down.add(p[num], 1);
        up.add(p[num], 1);
        up.add(p[num] + size[num], -1);
        return true;
    }
    
    bool unlock(int num, int user) {
        if (mark[num] != user) return false;
        mark[num] = -1;
        down.add(p[num], -1);
        up.add(p[num], -1);
        up.add(p[num] + size[num], 1);
        return true;
    }
    
    bool upgrade(int num, int user) {
        if (up.sum(p[num])) return false;
        int L = down.sum(p[num] - 1), R = down.sum(p[num] + size[num] - 1);
        if (L == R) return false;
        for (int i = 0; i < R - L; i += 1) {
            int k = down.query(L + 1);
            mark[q[k]] = -1;
            down.add(k, -1);
            up.add(k, -1);
            up.add(k + size[q[k]], 1);
        }
        lock(num, user);
        return true;
    }
};
 Comments
On this page
1993-树上的操作