2271-毯子覆盖的最多白色砖块数

给你一个二维整数数组 tiles ，其中 tiles[i] = [li, ri] ，表示所有在 li <= j <= ri 之间的每个瓷砖位置
j 都被涂成了白色。

同时给你一个整数 carpetLen ，表示可以放在 任何位置 的一块毯子的长度。

请你返回使用这块毯子，最多可以盖住多少块瓷砖。

示例 1：

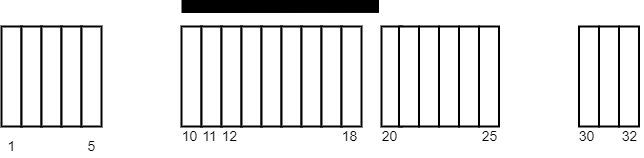
**输入：** tiles = [[1,5],[10,11],[12,18],[20,25],[30,32]], carpetLen = 10
**输出：** 9
**解释：** 将毯子从瓷砖 10 开始放置。
总共覆盖 9 块瓷砖，所以返回 9 。
注意可能有其他方案也可以覆盖 9 块瓷砖。
可以看出，瓷砖无法覆盖超过 9 块瓷砖。

示例 2：

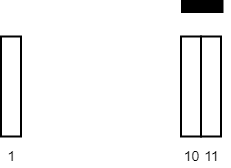
**输入：** tiles = [[10,11],[1,1]], carpetLen = 2
**输出：** 2
**解释：** 将毯子从瓷砖 10 开始放置。
总共覆盖 2 块瓷砖，所以我们返回 2 。

提示：

1 <= tiles.length <= 5 * 104
tiles[i].length == 2
1 <= li <= ri <= 109
1 <= carpetLen <= 109
tiles 互相 不会重叠 。

方法一：双指针

提示 1

一定存在至少一种覆盖砖块最多的方案，它的起始位置是在某一段连续瓷砖的第一个。

提示 1 解释

我们可以使用反证法证明。假设某一种起始位置不在某一段连续瓷砖第一个的覆盖方案覆盖的数量高于任何起始位置在连续瓷砖第一个的方案，则会有以下两种情况：

起始位置没有瓷砖，此时假设起始位置距离下一个瓷砖为 m（如果不存在下一段瓷砖，则覆盖数量一定为 0，不符合要求），那么我们将起始位置右移 m 格，由于移开的这 m 格没有瓷砖，因此数量一定不会减少，这就产生了矛盾；
起始位置在某段连续瓷砖的中间位置，此时假设起始位置距离该段瓷砖起始位置距离为 m，那么我们将起始位置左移 m 格，由于加入的这 m 格一定都有瓷砖，因此数量一定不会减少，这也产生了矛盾。

思路与算法

根据 提示 1，我们可以枚举所有连续白色瓷砖的起始点，并计算每种方案覆盖的瓷砖数量，同时维护最大值并最终返回。但如果我们对每个起始点都暴力计算瓷砖数量的话，时间复杂度显然不满足题目的要求。因此我们需要考虑优化计算的过程。

首先我们将每段瓷砖按照起始位置升序排序。我们用 n 表示连续瓷砖的数量。随后，我们从左至右枚举毯子的起始点对应的连续瓷砖下标 l，同时维护从左至右第一段无法完全覆盖的连续瓷砖的下标 r（如果能覆盖起始点右侧的所有瓷砖则 r = n）。当 l 增加时，r 显然不会减少，因此我们可以采用双指针的方法维护。

具体地，我们用 res 表示最多瓷砖数；为了方便计算，我们用 cnt 和 extra 分别表示当前完整覆盖的所有连续瓷砖段的瓷砖总数以及未完整覆盖部分的瓷砖数。即每次覆盖的瓷砖数为 cnt} + \textit{extra。

每当我们遍历到新的下标 l 时，如果 l \not= 0，则我们需要将 cnt 减去移出瓷砖段的瓷砖数量 tiles}[l - 1][1] - \textit{tiles}[l - 1][0] + 1，随后，我们尝试增加 r 直到覆盖完起点右侧的所有瓷砖（此时 r = n）或遇到无法完全覆盖的瓷砖。每当我们可以完全覆盖新的一段连续瓷砖时，我们将 cnt 加上该段瓷砖的数量 tiles}[r][1] - \textit{tiles}[r][0] + 1 并将 r 加上 1。

此时如果 r = n，则代表我们无法继续通过右移增加覆盖的数量，此时我们将 res 更新为它与 cnt 的最大值后，res 即为可覆盖瓷砖的最大值，我们直接返回 res 即可。

如果 r \not= n，我们还需要计算未完整覆盖部分的瓷砖数 extra，此时可能有两种情况：

毯子右端点没有到达下一段瓷砖的起始位置，此时 extra} = 0；
毯子右端点已经到达下一段瓷砖的起始位置，此时 extra} = \textit{tiles}[l][0] + \textit{carpetLen} - \textit{tiles}[r][0]。

事实上由于第一种情况时 tiles}[l][0] + \textit{carpetLen} - \textit{tiles}[r][0] 一定不大于 0，所以我们可以令

\textit{extra} = \max(0, \textit{tiles}[l][0] + \textit{carpetLen} - \textit{tiles}[r][0]).

在计算完成 cnt 和 extra 后，我们将 res 更新为它与 cnt} + \textit{extra 的最大值并继续遍历后续的 l （如有）。

当遍历完成所有 l 后，res 即为可覆盖瓷砖的最大值，我们返回该值作为答案。

代码

[sol1-C++]class Solution {
public:
    int maximumWhiteTiles(vector<vector<int>>& tiles, int carpetLen) {
        sort(tiles.begin(), tiles.end());   // 按照起始位置排序
        int n = tiles.size();
        int res = 0;   // 最多可以覆盖的瓷砖数量
        int cnt = 0;   // 当前可以完全覆盖的连续瓷砖段的瓷砖数总和
        int r = 0;   // 从左至右第一段无法完全覆盖的连续瓷砖的下标
        // 枚举起始点对应连续瓷砖段的下标
        for (int l = 0; l < n; ++l) {
            if (l) {
                cnt -= tiles[l-1][1] - tiles[l-1][0] + 1;
            }
            while (r < n && tiles[l][0] + carpetLen > tiles[r][1]) {
                cnt += tiles[r][1] - tiles[r][0] + 1;
                ++r;
            }
            if (r == n) {
                // 此时无法通过右移增加覆盖瓷砖数，更新最大值并返回即可
                res = max(res, cnt);
                return res;
            }
            int extra = max(0, tiles[l][0] + carpetLen - tiles[r][0]);   // 当前无法完全覆盖的连续瓷砖段的覆盖瓷砖数
            res = max(res, cnt + extra);
        }
        return res;
    }
};

[sol1-Python3]class Solution:
    def maximumWhiteTiles(self, tiles: List[List[int]], carpetLen: int) -> int:
        tiles.sort()   # 按照起始位置排序
        n = len(tiles)
        res = 0   # 最多可以覆盖的瓷砖数量
        cnt = 0   # 当前可以完全覆盖的连续瓷砖段的瓷砖数总和
        r = 0   # 从左至右第一段无法完全覆盖的连续瓷砖的下标
        # 枚举起始点对应连续瓷砖段的下标
        for l in range(n):
            if l:
                cnt -= tiles[l-1][1] - tiles[l-1][0] + 1
            while r < n and tiles[l][0] + carpetLen > tiles[r][1]:
                cnt += tiles[r][1] - tiles[r][0] + 1
                r += 1
            if r == n:
                # 此时无法通过右移增加覆盖瓷砖数，更新最大值并返回即可
                res = max(res, cnt)
                return res
            extra = max(0, tiles[l][0] + carpetLen - tiles[r][0])   # 当前无法完全覆盖的连续瓷砖段的覆盖瓷砖数
            res = max(res, cnt + extra)
        return res

复杂度分析

时间复杂度：O(n\log n)，其中 n 为 tiles 的长度。对 tiles 数组排序的时间复杂度为 O(n\log n)，双指针维护最多可覆盖数量的时间复杂度为 O(n)。
空间复杂度：O(\log n)，即为排序的栈空间开销。