LCP 02-分式化简

有一个同学在学习分式。他需要将一个连分数化成最简分数，你能帮助他吗？

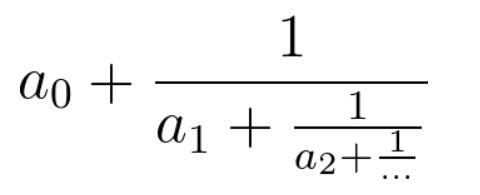
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2019/09/09/fraction_example_1.jpg)

连分数是形如上图的分式。在本题中，所有系数都是大于等于0的整数。

输入的cont代表连分数的系数（cont[0]代表上图的a0，以此类推）。返回一个长度为2的数组[n, m]，使得连分数的值等于n / m，且n, m最大公约数为1。

示例 1：

**输入：** cont = [3, 2, 0, 2]
**输出：** [13, 4]
**解释：** 原连分数等价于3 + (1 / (2 + (1 / (0 + 1 / 2))))。注意[26, 8], [-13, -4]都不是正确答案。

示例 2：

**输入：** cont = [0, 0, 3]
**输出：** [3, 1]
**解释：** 如果答案是整数，令分母为1即可。

限制：

cont[i] >= 0
1 <= cont的长度 <= 10
cont最后一个元素不等于0
答案的n, m的取值都能被32位int整型存下（即不超过2 ^ 31 - 1）。

大家好，这里是热爱算法的女孩子小爱，力扣杯即将来袭，小爱准备学习往届真题，并与大家一起分享！关注小爱老师的算法课堂，分享高质量算法视频与文字题解，欢迎大家多多支持，与小爱互动呀！

题目分析：模拟、最大公约数

本题让我们进行连续的分数化简，我们可以发现，这是一个循环过程。在对原数组进行逆序操作后，我们会发现，第 i 轮实际上是对 a[i] + c}{d 的式子进行通分、化简、取倒数，得到的结果将作为第 i + 1 轮的 c}{d 。

算法细节：

在代码实现中，第一轮我们要化简的是 a[1] + 1}{a[0]，所以我们定义初始值为 c = 1, d = a[0]。

每一轮，我们通分 a[i] + c}{d} = a[i] \times d + c}{d，并通过分子分母同除最大公约数 g = gcd(a[i] \times d + c, d) 得到最简分数。再取倒数，并将得到的分子、分母赋值给 c, d，以便下一轮计算使用。

特别地，根据题目给定的公式，最后一轮化简是没有取倒数这一环节的。但在我们的代码中，每次循环最后都要进行一次取倒数。所以最后一轮多做了一次取倒数，我们在最后，需要重新互换 c, d 的值，得到的才是最终结果。

代码：

class Solution {
public:
    vector<int> fraction(vector<int>& cont) {
        reverse(cont.begin(), cont.end());
        // 初始值：a[1] + 1 / a[0]
        int c = 1, d = cont[0];
        int n = cont.size();
        for(int i = 1; i < n; i++) {
            // a[i] + c / d = (a[i] * d + c) / d
            int new_c = cont[i] * d + c;
            int new_d = d;

            // 化简最简分数
            int g = gcd(new_c, new_d);
            new_c /= g;
            new_d /= g;

            // 取倒数，赋值给新的 c / d
            c = new_d;
            d = new_c;
        }

        // 最后一轮，没有取倒数这一步
        swap(c, d);

        return vector<int>{c, d};

    }
};

复杂度分析：

时间复杂度：O(n)
空间复杂度：O(n)