LCP 82-万灵之树

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 17:01:06 2023-09-13 17:01:06 Updated    

探险家小扣终于来到了万灵之树前，挑战最后的谜题。 已知小扣拥有足够数量的链接节点和 n 颗幻境宝石，gem[i] 表示第 i
颗宝石的数值。现在小扣需要使用这些链接节点和宝石组合成一颗二叉树，其组装规则为： - 链接节点将作为二叉树中的非叶子节点，且每个链接节点必须拥有 2
个子节点； - 幻境宝石将作为二叉树中的叶子节点，所有的幻境宝石都必须被使用。 能量首先进入根节点，而后将按如下规则进行移动和记录： -
若能量首次到达该节点时： - 记录数字 1； - 若该节点为叶节点，将额外记录该叶节点的数值； -
若存在未到达的子节点，则选取未到达的一个子节点（优先选取左子节点）进入； - 若无子节点或所有子节点均到达过，此时记录
9，并回到当前节点的父节点（若存在）。 如果最终记下的数依序连接成一个整数 num，满足 num \mod~p=target，则视为解开谜题。
请问有多少种二叉树的组装方案，可以使得最终记录下的数字可以解开谜题 注意： - 两棵结构不同的二叉树，作为不同的组装方案 -
两棵结构相同的二叉树且存在某个相同位置处的宝石编号不同，也作为不同的组装方案 - 可能存在数值相同的两颗宝石 示例 1： > 输入：gem = [2,3] > p = 100000007 > target = 11391299 > > 输出：1 > > 解释： > 包含 2
个叶节点的结构只有一种。 > 假设 B、C 节点的值分别为 3、2，对应 target 为 11391299，如下图所示。 > 11391299 %
100000007 = 11391299，满足条件; > 假设 B、C 节点的值分别为 2、3，对应 target 为 11291399; >
11291399 % 100000007 = 11291399，不满足条件； > 因此只存在 1 种方案，返回 1 万灵 (1).gif{:height=300px}
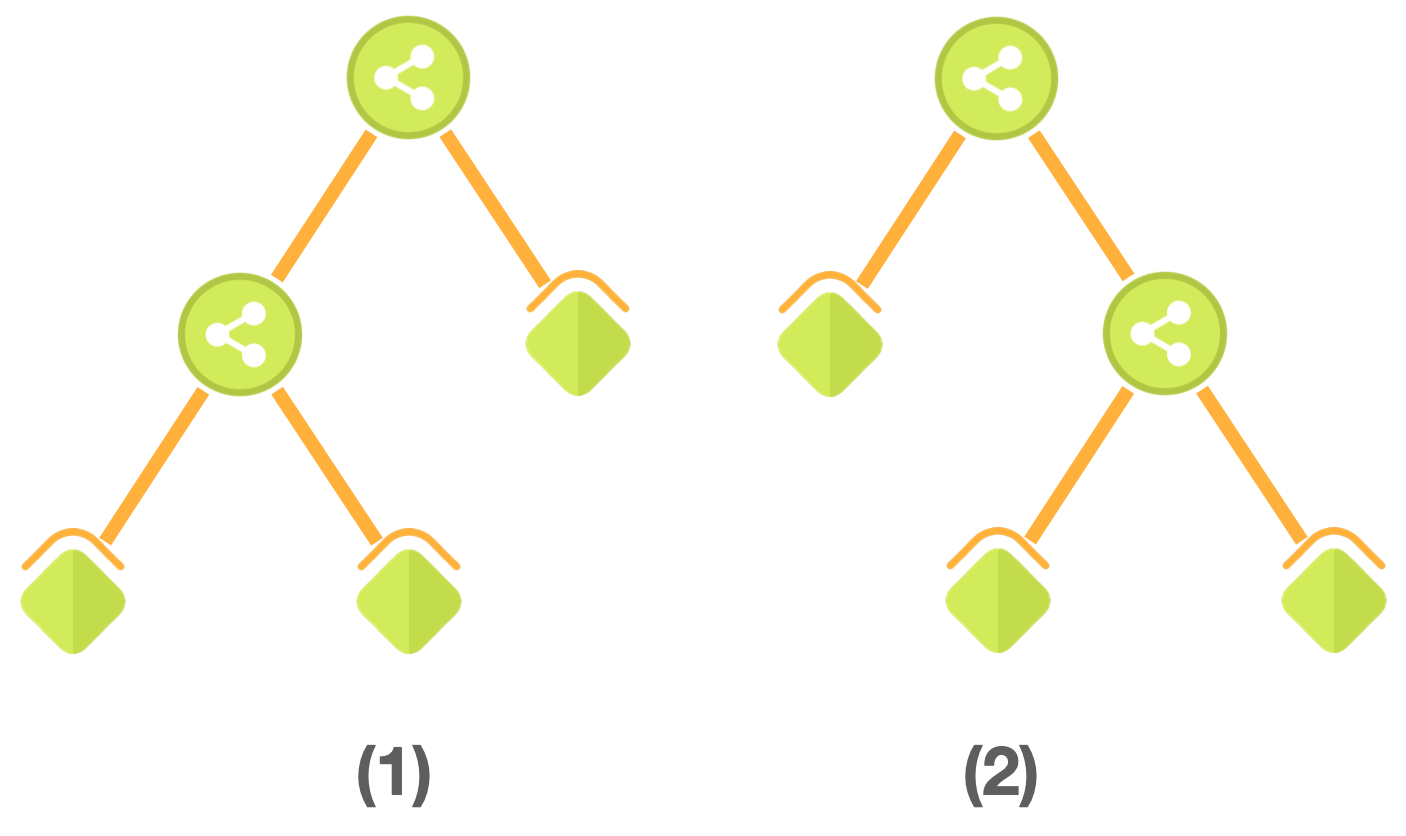
示例 2： > 输入：gem = [3,21,3] > p = 7 > target = 5 > > 输出：4 > > 解释： 包含
3 个叶节点树结构有两种，列举如下： 满足条件的组合有四种情况： > 当结构为下图（1）时：叶子节点的值为 [3,3,21] 或
[3,3,21]，得到的整数为 11139139912199。 > 当结构为下图（2）时：叶子节点的值为 [21,3,3] 或
[21,3,3]，得到的整数为 11219113913999。
![image.png](https://pic.leetcode.cn/1682322894-vfqJIV-
image.png){:width=500px} 提示： - 1 <= gem.length <= 9 - 0 <= gem[i] <= 10^9 - 1 <= p <= 10^9，保证 p 为素数。 - 0 <= target < p - 存在 2 组
gem.length == 9 的用例

题解

算法一
暴力搜索所有方案。我们需要枚举所有包含 n 个叶节点的完整二叉树的形态，以及所有 1 ~ n 的排列。包含 n 个叶节点的完整二叉树的数量为卡特兰数 C_{n-1，而排列有 n! 种可能。使用一些技巧，可以在均摊 O(1) 的时间内计算出每个方案对应的数 \bmod~p 的值，例如使用集合动态规划或精妙的 dfs 写法。

根据斯特林公式，可知渐近复杂度为 C_{n-1}\cdot n!=(4^n/n^{3/2})\cdot (\sqrt{n}\cdot (n/e)^n)=(4/e)^n\cdot n^{n-1。

具体地，n=8 时总方案数为 429\cdot 40320=17297280，而 n=9 时为 1430\cdot 362880=518918400，变大了 30 倍。即使在 n=8 时有机会优化通过，但这一复杂度增长极快，当 n=9 时就难以接受了。

因为目标是对所有满足条件的方案进行计数，所以对这个搜索进行剪枝似乎是困难的，我没有什么好的想法。如果你没有预先估计复杂度就开始写，然后因为沉没成本，又花了很多时间在暴搜的基础上设计剪枝方案或进行常数优化，那你就上钩了。

算法二
正解是复杂度更优的做法。核心思想是使用树的重心进行分治，并使用 meet-in-the-middle 的技巧合并两部分的答案。考虑找到完整二叉树的重心 v (只考虑叶节点的重量，忽略内部节点)。那么或者 v 存在一个儿子 u 满足以 u 为根的子树的叶子数在 [\dfrac{1/3}n,\dfrac{1/2}n] 范围内，或者以 v 为根的子树的叶子数 \leq \dfrac{2/3}n，即 v 上方的连通块的叶子数在 [\dfrac{1/3}n,\dfrac{1/2}n+1] 范围内。

若为第一种情况，则可以预先搜索出所有以 u 为根，叶子数 \leq \dfrac{1/2}n 的完整二叉树以及其中节点所用到的数字集合所对应的答案。还需要将 u 下方的子树缩成一个叶节点，记为变量 x，搜索 u 上方连通块的情况，叶子数 \leq \dfrac{2/3}n+1。这部分的结果可以表示成 v_1,x,v_2 依次连接的形式，v_1,v_2 已知。我们同时记录下 v_2 的长度，这样给定 x 的值后就可以计算出整体表示的数。知道上方部分的结果后可以利用逆元解方程，O(1) 算出下方部分应该得到的值 x，用哈希表在下方部分的结果中查找。对第二种情况的处理类似，需要搜索 v 下方叶子数 \leq \dfrac{2/3}n 的子树及 v 上方的连通块。一个小细节是需要对树的形态分类讨论，避免重复计数。
注：也可以自顶向下地计算 x。第一名的队伍的实现方式很优雅，推荐大家看一下。

总复杂度为 O\left(\sum_{i=1}^{2n/3}\dfrac{n!}{(n-i)!}\cdot C_{i-1}\right)=O\left(c^n\cdot n^{2n/3-1.5}\right)，其中常数 c=\dfrac{3^{1/3}\cdot 4^{2/3} }{e^{2/3} }\approx 1.866。这个复杂度是比算法一更优的。(比较复杂度时注意最重要的部分，n^{2n/3}<n^n.)

具体地，当 n=9 时我们只需要对 6 个叶子的完整二叉树进行搜索。可以对切下来作为下方的子树进行如下分类讨论(对以上通用思路作了一点修改，这样常数小一点)：

  1. 恰有 6 个叶节点。
  2. 恰有 5 个叶节点，且它的兄弟子树有 \geq 2 个叶子。
  3. 恰有 4 个叶节点，且它的兄弟子树有 3 个叶子。
  4. 恰有 4 个叶节点，且它的兄弟子树在它右边并有 4 个叶子。

不难验证这样分类是不重不漏的。这对应着上方与下方一共有大约三百万种方案。我们放了标程 15 倍的时限。

注：当模数 p 不为素数时，我们仍然可以通过逆元 + 中国剩余定理反向计算出下方部分应该得到的值 x，从而合并两部分的答案。对于本题，如果想直接使用逆元的话，需要特判 p=2 与 p=5 这两个与 10 不互质的素数(简单地考虑连成数字的最后一位即可，一定为 9)。考虑到这题已经比较麻烦了，就没有额外增加 p 任意时的思维难度。

算法三
还可以有另一种 meet-in-the-middle 的合并方法。先枚举每种包含 n 个叶节点的完整二叉树的形状 T。在 T 确定下来后，再枚举 \binom{n}{n/2 种将数组 a[1..n] 划分成等大小的两半的方案。划分方法确定后，对每一半分别枚举 (\dfrac{n}{2})! 种排列，依序对应到前一半或后一半的叶子上。最后使用 meet-in-the-middle 合并两半的结果。

总复杂度为 O\left(C_{n-1}\cdot \binom{n}{n/2}\cdot (\dfrac{n}{2})!\right)=O(c_1^n\cdot n^{n/2})，其中常数 c_1=\dfrac{4\cdot 2^{1/2} }{e^{1/2} }\approx 3.432。

这个算法的理论渐近复杂度更优，但对于本题数据范围的实际表现不如算法二，不能确保通过(有一些队伍使用了这个方法，需要实现比较好)。具体地，当 n=9 时我们需要考虑大约两千万种方案。

算法四(算法一)
暴力优化，返璞归真。虽然我们的预期是没有选手在比赛中使用暴力 AC 本题，不过我出题的时候也花了一些时间试验，发现极致优化的暴力事实上是可以在时限内轻松通过的。
(以下均为 C++ 的结果；我对其他语言的常数优化技巧不是很熟，如果其他语言有暴力能过的话欢迎评论告知。注意 python 是不能使用 numpy 的。)

考虑使用集合动态规划实现暴力，这样代码还是挺短的，而且常数会比 dfs 好一些。方法是用一个列表 c_i 表示使用二进制集合 i 代表的宝石能组合出的所有数字。c_i 可以由所有的 c_j 和 c_{i-j 计算出，其中 j\subseteq i 表示左子树中的宝石集合为 j，那么右子树中的宝石集合为 i-j。

我对这个思路的第一版实现跑了 10s，不够快。需要加一些常数优化。列举如下：

  1. 用数组代替 vector。
  2. 注意到整个程序的瓶颈是最后合并大小为 n-1 和 1 的两棵子树(一共有 n 种组合)。这个时候不需要先合并出整棵树可以取到的值再查询，而是直接统计答案，从左子树中枚举一个值，在右子树的列表中查询对应的值。这样会更快。
  3. 当我们合并左右子树时，外层循环枚举小子树，内层枚举大子树。这样内层循环会比较并行，可以给之后的优化带来帮助。
  4. 加速取模。我一开始试的是 Barrett 约减，不过后来发现 这个 批量对固定乘数模数进行乘模的技巧会更快。
  5. 这个时候速度上已经可以通过了，但会爆内存。我们将大小为 n-1 的子树对应的列表分成两批计算，算完第一批后直接扔掉，这样内存正好卡在 500MB 内。
  6. 查询时，枚举一棵子树中的值 v，用逆元算出另一棵子树中需要的值 r_1 和 r_2，这样内层循环中只需要比较操作：
    1
    for (uint *J=c[i-j],*end=c[i-j]+c1[i-j];J!=end;++J)ans+=(*J==r1)+(*J==r2)
    这样写会很快。原则上说，尽量在算式中分离变量，在外层循环把需要的计算进行预处理。
    (7). 考虑到选手一般不会使用 SIMD，公平起见我也没有尝试指令集的技巧。不过看起来在以上优化过后，目前的写法是挺容易并行的。

这样暴力运行的总时间仅为 1s(可进一步优化到 0.6s，不过不太公平)，而我们考虑到一般选手对标算实现的速度，给 C++ 设定的时限为 4s。

最后放上不同解法的代码实现：

[code -std(算法二)]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include<bits/stdc++.h>
using namespace std;
namespace Hash{
	typedef unsigned int uint;
	const uint S=16,S1=32-S,M=1996090921;
	#define H(x) ((uint)x*M>>S1)
	struct node{int x,y,t;}h[(1<<S)+105];
	int T=1;
	inline void insert(int x){
		node *p=h+H(x);
		for (;p->t==T;++p)
			if (p->x==x){++p->y; return;}
		p->t=T; p->x=x; p->y=1;
	}
	inline int find(int x){
		for (node *p=h+H(x);p->t==T;++p)
			if (p->x==x)return p->y;
		return 0;
	}
	#undef H
} using namespace Hash;
typedef long long ll;
#define pop __builtin_popcount
const int N=9,M0=205;
int pow10[M0],pinv[M0],l[N],len[1<<N],n,ans,p,r,B;
struct Node{int v1,v2,l;};
int log10(int n){return n<10?1:log10(n/10)+1;}
template<class T> T extend_gcd(T a,T b,T &x,T &y){
	if (!b){x=1;y=0;return a;}
	T res=extend_gcd(b,a%b,y,x); y-=x*(a/b);
	return res;
}
template<class T> T inv(T a,T M){T x,y; extend_gcd(a,M,x,y); return (x%M+M)%M;}
ll fac(int n){ll res=1; while (n)res*=n--; return res;}
ll C(int n,int m){ll res=1; for (int i=1;i<=m;++i)res=res*(n-i+1)/i; return res;}
class Solution {
public:
	vector<int> c[1<<N];
	vector<Node> d[1<<(N+1)];
	template<class F1,class F2,class F3>
	void calc(int t0,F1 f1,F2 f2,F3 f3){
		for (int i=(1<<n)+1;i<(1<<(n+1));++i)d[i].clear();
		for (int i=1<<n;i<(1<<(n+1));++i)if (pop(i)<=t0){
			for (int j=(i-1)&i,_f2;j>>n;j=(j-1)&i)if ((_f2=f2(i,j))||f1(i,j))
				for (auto &t:d[j]){
					int l1=len[j-(1<<n)]-t.l+2*(j>(1<<n));
					for (auto &v2:c[i-j]){
						d[i].push_back({(t.v1+pow10[l1])%p,
							int(((ll)t.v2*pow10[len[i-j]+1]+(ll)v2*10+9)%p),t.l+len[i-j]+1});
						if (!_f2)d[i].push_back({int((t.v1+pow10[l1+len[i-j]]+(ll)v2*pow10[l1])%p),
							int(((ll)t.v2*10+9)%p),t.l+1});
					}
				}
			int j=(1<<(n+1))-1-i; ++T;
			if (f3(j))continue;
			for (auto &v:c[j])insert(v);
			for (auto &t:d[i])ans+=find((((ll)r-t.v2-(ll)t.v1*pow10[len[j]+t.l])%p+p)*pinv[t.l]%p);
		}
	}
	int treeOfInfiniteSouls(vector<int>& a,int p,int r) {
		n=a.size(); ans=0; B=(n+2)/3; ::p=p; ::r=r;
		if (p==2||p==5)return p==2&&r==1||p==5&&r==4?C((n-1)*2,n-1)/n*fac(n):0;
		pow10[0]=1%p; for (int i=1;i<M0;++i)pow10[i]=(ll)pow10[i-1]*10%p;
		for (int i=0;i<M0;++i)pinv[i]=inv(pow10[i],p);
		for (int i=0;i<n;++i)l[i]=log10(a[i]);
		for (int i=1;i<(1<<n);++i){
			len[i]=(pop(i)*2-1)*2;
			for (int j=0;j<n;++j)if (i&(1<<j))len[i]+=l[j];
		}
		for (int i=0;i<n;++i)c[1<<i].push_back(((ll)a[i]*10+pow10[l[i]+1]+9)%p);
		for (int i=1;i<(1<<n);++i)if (pop(i)<=B*2){  //component below u
			int t=pow10[len[i]-1]+9;
			for (int j=(i-1)&i;j;j=(j-1)&i)
				if (n==9||pop(i)<max((n+1)/2,2)||max(pop(j),pop(i-j))<=min(B,(n-1)/2))
					for (auto &v1:c[j]){
						ll t1=(ll)v1*pow10[len[i-j]+1]+t;
						for (auto &v2:c[i-j])c[i].push_back(((ll)v2*10+t1)%p);
					}
		}
		d[1<<n].push_back({0,0,0}); //component above u
		auto yes=[](int x,int y=0){return 1;}; auto no=[](int x,int y=0){return 0;};
		if (n==9)
			calc(4,yes,no,[](int j){return pop(j)!=6;}), //remove size 6
			calc(5,[](int i,int j){return j!=(1<<n)||pop(i-j)>=2;}, //remove size 5
				 no,[](int j){return pop(j)!=5;}),
			calc(6,[](int i,int j){return j!=(1<<n)||pop(i-j)==3;}, //remove size 4
				 [](int i,int j){return j==(1<<n)&&pop(i-j)==4;},
				 [](int j){return pop(j)!=4;});
		else calc(n/2+1,yes,[](int i,int j){return n%2==0&&pop(j)==1&&pop(i-j)==n/2;},
				 [](int j){return pop(j)<(n+1)/2||pop(j)>B*2;});
		return ans;
	}
};
[code - 验题人的C++(AC)]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
// 算法二
inline int int_len(int x){
    if (x < 10) return 1;
    if (x < 100) return 2;
    if (x < 1000) return 3;
    if (x < 10000) return 4;
    if (x < 100000) return 5;
    if (x < 1000000) return 6;
    if (x < 10000000) return 7;
    if (x < 100000000) return 8;
    if (x < 1000000000) return 9;
    return 10;
}
inline int lowbit(int x){
    return x & (-x);
}
class Solution {
    unordered_map<int, int> mps[520];
    int thislen[520];
    int tens[505];
    int tens_inv[505];
    long long C[15];
    int M;
    unordered_set<int> targs[520];
    int modadd(int x, int y){
        return (x + y >= M ? x + y - M: x + y);
    }
    int poww(int a, int b){
        int res = 1;
        while (b > 0){
            if (b & 1)
                res = 1ll * res * a % M;
            a = 1ll * a * a % M, b >>= 1;
        }
        return res;
    }
    int leaf(int x, int l){
        int tmp = modadd(9 % M, 10ll * x % M);
        tmp = modadd(tmp, tens[l + 1]);
        return tmp;
    }
public:
    int treeOfInfiniteSouls(vector<int>& a, int p, int r) {
        // preprocess
        C[0] = 1;
        for (int i = 1; i <= 8; ++i){
            C[i] = 0;
            for (int j = 0; j < i; ++j){
                C[i] += C[j] * C[i - j - 1];
            }
        }

        int n = a.size();
        int nhalf = max(1, n >> 1);
        if (nhalf & 1) ++nhalf;
        if (p == 5) nhalf = n;

        if (p == 2){
            // do special judge here
            if (r == 0) return 0;

            int perm = 1;
            for (int i = 2; i <= n; ++i){
                perm *= i;
            }
            return perm * C[n - 1];
        }

        M = p;
        tens[0] = 1;
        for (int i = 1; i <= 500; ++i)
            tens[i] = 10ll * tens[i - 1] % p;
        tens_inv[1] = poww(10 % M, M - 2);
        for (int i = 2; i <= 500; ++i)
            tens_inv[i] = 1ll * tens_inv[1] * tens_inv[i - 1] % p;

        memset(thislen, 0, sizeof(thislen));
        thislen[0] = -2;
        for (int i = 1; i < (1 << n); ++i){
            int lb = lowbit(i);
            thislen[i] = thislen[i - lb] + int_len(a[__builtin_ctz(lb)]) + 4;
        }
        
        // get all half first
        for (int i = 1; i < (1 << n); ++i){
            if (__builtin_popcount(i) > nhalf){
                continue;
            }

            if (!(i & (i - 1))){
                // 2^some
                int val = a[__builtin_ctz(i)];
                int l = int_len(val);
                mps[i][leaf(val, l)] = 1;
                continue ;
            }
            for (int j = (i - 1) & i; j > 0; j = (j - 1) & i){
                int k = i - j;
                // size + 2(2size - 1)
                // int lj = thislen[j] + ((__builtin_popcount(j) << 2) - 2);
                int lj = thislen[j];
                int tenj = tens[lj + 1];
                // int lk = thislen[k] + ((__builtin_popcount(k) << 2) - 2);
                int lk = thislen[k];
                int tenk = tens[lj + lk + 1];
                for (auto& pj: mps[j]){
                    // pk, pj
                    int tmp = modadd(9 % M, 10ll * pj.first % M);
                    tmp = modadd(tmp, tenk);
                    for (auto& pk: mps[k]){
                        int tmp2 = modadd(tmp, 1ll * pk.first * tenj % M);
                        auto iter = mps[i].find(tmp2);
                        int cnt = 0;
                        if (iter != mps[i].end()){
                            cnt = iter->second;
                        }
                        mps[i][tmp2] = cnt + pj.second * pk.second;
                    }
                }
            }
        }

        // survey
        targs[(1 << n) - 1].insert(r);
        for (int q = n; q > nhalf; --q){
            for (int i = 0; i < (1 << n); ++i){
                if (__builtin_popcount(i) != q){
                    continue;
                }

                for (int j = (i - 1) & i; j > 0; j = (j - 1) & i){
                    int k = i - j;
                    int jsize = __builtin_popcount(j);
                    if (q - jsize <= nhalf){
                        continue;
                    }

                    // avoid duplicate enumeration
                    bool norep = (jsize == (q - jsize));

                    int lj = thislen[j];
                    int lk = thislen[k];
                    int tenk = tens[lj + lk + 1];
                    for (int tg: targs[i]){
                        tg = modadd(tg, M - tenk);
                        tg = modadd(tg, M - (9 % M));

                        for (auto& pj: mps[j]){
                            // j as lower part
                            int tg1 = modadd(tg, M - (10ll * pj.first % M));
                            tg1 = 1ll * tg1 * tens_inv[lj + 1] % M;
                            targs[k].insert(tg1);

                            // j as higher part
                            if (!norep){
                                int tg2 = modadd(tg, M - (1ll * pj.first * tens[lk + 1] % M));
                                tg2 = 1ll * tg2 * tens_inv[1] % M;
                                targs[k].insert(tg2);
                            }
                        }
                    }
                }                
            }
        }

        // stat
        for (int q = nhalf + 1; q <= n; ++q){
            for (int i = 0; i < (1 << n); ++i){
                if (__builtin_popcount(i) != q){
                    continue;
                }

                for (int j = (i - 1) & i; j > 0; j = (j - 1) & i){
                    int k = i - j;
                    int jsize = __builtin_popcount(j);
                    // only enumerate those with <= 1/2 size
                    if (jsize > (q >> 1)){
                        continue;
                    }

                    // avoid duplicate enumeration
                    bool norep = (jsize == (q - jsize));

                    int lj = thislen[j];
                    int lk = thislen[k];
                    int tenk = tens[lj + lk + 1];
                    for (int tg: targs[i]){
                        int cnt = 0;
                        if (mps[i].count(tg)){
                            cnt = mps[i][tg];
                        }

                        int ori_tg = tg;
                        tg = modadd(tg, M - tenk);
                        tg = modadd(tg, M - (9 % M));

                        for (auto& pj: mps[j]){
                            // j as lower part
                            int tg1 = modadd(tg, M - (10ll * pj.first % M));
                            tg1 = 1ll * tg1 * tens_inv[lj + 1] % M;
                            auto iter = mps[k].find(tg1);
                            if (iter != mps[k].end()){
                                cnt += (iter->second) * pj.second;
                            }
                            
                            if (!norep){
                                // j as higher part
                                int tg2 = modadd(tg, M - (1ll * pj.first * tens[lk + 1] % M));
                                tg2 = 1ll * tg2 * tens_inv[1] % M;
                                auto iter = mps[k].find(tg2);
                                if (iter != mps[k].end()){
                                    cnt += (iter->second) * pj.second;
                                }
                            }
                        }

                        mps[i][ori_tg] = cnt;
                    }
                }
            }
        }

        int ans = 0;
        auto iter = mps[(1 << n) - 1].find(r);
        if (iter != mps[(1 << n) - 1].end()){
            ans += iter->second;
        }
        return ans;
    }
};
[code - 暴力优化(AC)]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
#include<bits/stdc++.h>
using namespace std;
typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned __int128 u128;
#define pop __builtin_popcount
const int N=10,M=205;
int pow10[M],pinv[M],l[N],len[1<<N],t1,p10[1<<N],p10_[1<<N];
int log10(int n){return n<10?1:log10(n/10)+1;}
template<class T> T extend_gcd(T a,T b,T &x,T &y){
	if (!b){x=1;y=0;return a;}
	T res=extend_gcd(b,a%b,y,x); y-=x*(a/b);
	return res;
}
template<class T> T inv(T a,T M){T x,y; extend_gcd(a,M,x,y); return (x%M+M)%M;}
ll fac(int n){ll res=1; while (n)res*=n--; return res;}
ll C(int n,int m){ll res=1; for (int i=1;i<=m;++i)res=res*(n-i+1)/i; return res;}
uint _Pool[200000005],*p1,*c[1<<N],c1[1<<N],*pend;
class Solution {
public:
	//__attribute__((no_sanitize_address,no_sanitize_memory))
	int treeOfInfiniteSouls(vector<int>& a,int p,int r) {
		int n=a.size(); uint ans=0;
		if (p==2||p==5)return p==2&&r==1||p==5&&r==4?C((n-1)*2,n-1)/n*fac(n):0;
		//if (n==9&&p==2)return 518918400;
		//if (n==9&&p==100000007)return 21;
		pow10[0]=1%p; for (int i=1;i<M;++i)pow10[i]=(ll)pow10[i-1]*10%p;
		for (int i=0;i<M;++i)pinv[i]=inv(pow10[i],p);
		for (int i=0;i<n;++i)l[i]=log10(a[i]);
		for (int i=1;i<(1<<n);++i){
			len[i]=(pop(i)*2-1)*2;
			for (int j=0;j<n;++j)if (i&(1<<j))len[i]+=l[j];
		}
		for (int i=1;i<(1<<n);++i)p10[i]=pow10[len[i]-1],p10_[i]=pow10[len[i]+1];
		ull P1=(((u128)10<<64)+p-1)/p;
		for (int I=0;I<=1;++I){
			if (n<9&&I)break;
			p1=!I?_Pool:pend;
			for (int i=0;i<n;++i){
				c[1<<i]=p1++; c1[1<<i]=1;
				c[1<<i][0]=((ll)a[i]*10+pow10[l[i]+1]+9)%p;
			}
			if (n==1)return c[1][0]==r;
			for (int K=2;K<=n;++K){
				if (n==9&&K==n-1)pend=p1;
				for (int i=1;i<(1<<n);++i)if (pop(i)==K){
					uint add=(p10[i]+9)%p;
					if (n==9&&I==1&&pop(i)<n-1)continue;
					c[i]=p1; c1[i]=0;
					if (n==9&&pop(i)==n-1&&
						((!I&&__builtin_ctz(~i)<=4)||(I&&__builtin_ctz(~i)>4)))continue;
					uint *_c=p1,*c0=c[i];
					for (int j=(i-1)&i;j;j=(j-1)&i)
						if (c1[j]<c1[i-j]||c1[j]==c1[i-j]&&j<i-j){
							if (i==(1<<n)-1){
								//continue;
								if (I==1&&pop(j)!=n-1&&pop(i-j)!=n-1)continue;
								for (uint *I=c[j];I<c[j]+c1[j];++I){
									uint v1=*I;
									uint t1=((ull)v1*pow10[len[i-j]+1]+add)%p;
									uint add1=((ull)v1*10+add)%p,pow1=p10_[j];
									uint r1=(ull)(r+p-t1)*pinv[1]%p,r2=(ull)(r+p-add1)*inv((int)pow1,p)%p;
									if (r1!=r2){
                                        uint *J=c[i-j],*end=c[i-j]+c1[i-j];
                                        *end=r1; ++end;
                                        for (;J!=end;++ans,++J)
                                            while (*J!=r1&&*J!=r2)++J;
                                        --ans;
                                    }
									else for (uint *J=c[i-j],*end=c[i-j]+c1[i-j];J!=end;++J)
										ans+=(*J==r1)+(*J==r2);
								}
							}
							else for (uint *I=c[j];I<c[j]+c1[j];++I){
								uint v1=*I;
								uint t1=((ull)v1*pow10[len[i-j]+1]+add)%p;
								uint add1=((ull)v1*10+add)%p,pow1=p10_[j];
								ull P2=(((u128)pow1<<64)+p-1)/p;
								for (uint *J=c[i-j],*end=c[i-j]+c1[i-j];J!=end;++J){
									uint v2=*J;
									*c0=(uint)(v2*P1*(u128)p>>64)+t1;
									if (*c0>=p)*c0-=p; ++c0;
									*c0=(uint)(v2*P2*(u128)p>>64)+add1;
									if (*c0>=p)*c0-=p; ++c0;
								}
							}
						}
					c1[i]=c0-_c; c[i]=_c; p1+=c1[i]+1;
				}
			}
		}
		return ans;
	}
};
[code - 验题人的py(AC)]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
# 算法二
import cProfile
import time
from collections import *
import itertools
from functools import *
from typing import *

M=205
pow10=[0]*M
pinv=[0]*M
# 扩展欧几里得求逆元
def exgcd(a, b):
    if b == 0:
        return 1, 0, a
    else:
        x, y, q = exgcd(b, a % b)
        x, y = y, (x - (a // b) * y)
        return x, y, q

# 扩展欧几里得求逆元
@cache
def ModReverse(a,p):
    x, y, q = exgcd(a,p)
    if q != 1:
        raise Exception("No solution.")
    else:
        return (x + p) % p #防止负数
@cache 
def fa(n):
    if n==1:
        return 1
    res = 0
    for i in range(1,n):
        res += fa(i)*fa(n-i)
    return res

@cache
def bin_num(val):
    return val.bit_count()
    #return bin(val).count('1')

class Solution:
    '''@cache
    def pow10(self, val, mod):
        return pow(10, val, mod)'''
    

    #@profile
    def treeOfInfiniteSouls(self, a: List[int], p: int, r: int) -> int:
        '''if len(a)==9:
            if p==90007: return 5762
            if p==2: return 518918400
            if p==998244353: return 9'''
        start=time.time()
        self.MOD = p
        n = len(a) 
        if p==2:
            if r==1:
                return math.perm(n)*fa(n) 
            return 0
        if p==5:
            if r==4:
                return math.perm(n)*fa(n) 
            return 0  

        pow10[0]=1%p
        for i in range(1,M): pow10[i]=pow10[i-1]*10%p
        for i in range(M): pinv[i]=ModReverse(pow10[i],p)

        max_num = 6
        m = 1<<n 
        flist = defaultdict(list) # []
        lenlist = defaultdict(int)
        for i in range(n):
            s = f'1{a[i]}9'
            val = int(s) % self.MOD 
            flist[1<<i].append(val)
            lenlist[1<<i] = len(s)
        for i in range(1, m):
            if i in flist or bin_num(i)> max_num:
                continue
            for j in range(1,i):
                if (j|i)^i:
                    continue
                len1, len2 = lenlist[j], lenlist[i-j]
                start_val = 9 + pow10[len1+len2+1]
                lenlist[i] = lenlist[j] + lenlist[i-j] + 2
                bb=flist[i]
                p0=pow10[len2+1]
                for v1 in flist[j]:
                    oval = start_val + v1 * p0
                    #oval = (start_val + v1 * pow10[len2+1])%p
                    #flist[i].extend([(oval + v2 * 10)%p for v2 in flist[i-j]])
                    for v2 in flist[i-j]:
                        #bb.append((start_val + v1 * p0 + v2 * 10)%p)
                        bb.append((oval + v2 * 10)%p)
        
        self.numlist = {k: Counter(v)  for k,v in flist.items()}
        if n <= 6:
            return self.numlist.get(m-1, {}).get(r, 0)
        self.flist = flist
        #print('time: ',time.time() - start); start=time.time()
        self.lenlist = lenlist 
        self.res = 0 
        self.r = r 
        # 3, [6]  
        self.calcs(n, 6, lambda n,x,y: True)
        # print(self.res)
        #print('time1: ',time.time() - start); start=time.time()
        # 4, [5], bro >= 2
        self.calcs(n, 5, lambda n,x,y:  x!=(1<<n) or bin_num(y)>=2)
        # end = time.time()
        # print(self.res)
        #print('time2: ',time.time() - start); start=time.time()
        # # 5, [4], bro >= 3 and <= 4 
        self.calcs(n, 4, lambda n,x,y:  x!=(1<<n) or bin_num(y) in (3,4))
        # end = time.time()
        # print(self.res)
        #print('time3: ',time.time() - start); start=time.time()
        return self.res 

    #@profile
    def calcs(self, n, num, check_func):
        #_pow10=pow10.copy()
        pow10[0]=1%self.MOD
        for i in range(1,M): pow10[i]=pow10[i-1]*10%self.MOD
        t0=time.time()
        # 选择 num 个点合并组成 sub
        # n-num 个点 + sub 构成完整的树 
        #g = defaultdict(list)
        g=[[] for i in range(1<<(n+1))]
        g[1<<n] = [[0,0,0,0]]
        count_res = 0
        for k in range((1<<n)+1 , 1<<(n+1)): # 最高位表示有 sub 点
            one_num = bin_num(k)
            if one_num > n - num + 1:
                continue

            i = (k-1)&k
            while i>=(1<<n):
                j = k-i
                if not check_func(n, i, j):
                    i = (i-1)&k
                    continue 
                # print(k,i,j, bin(k), bin(i), bin(j), len(g[i]))
                # input()
                L=self.lenlist[j]
                for l,r, llen, rlen in g[i]:
                    #l,r, llen, rlen = info 
                    xnewl = pow10[llen] + l  
                    xnewr = 9 + r * pow10[self.lenlist[j]+1]# % self.MOD
                    ynewl = l + pow10[self.lenlist[j]+llen]
                    ynewr = 9 + r * 10
                    cc=[xnewl, 0, llen+1, rlen+L+1]
                    p0=pow10[llen]
                    l0=llen+self.lenlist[j]+1
                    ee=[0, ynewr, l0, rlen+1]
                    for v in self.flist[j]:
                        # 1 i j 9
                        dd=cc.copy()
                        dd[1]=(xnewr + v*10)%self.MOD
                        g[k].append(dd)
                        #g[k].append([xnewl, (xnewr + v*10)%self.MOD, llen+1, rlen+self.lenlist[j]+1])
                        
                        # 1 j i 1
                    if i!=(1<<n) or num != 4 or j.bit_count() != 4: # 防止出现 4 - 4 重复， 注意加特殊用例
                        for v in self.flist[j]:
                            #newl = (ynewl + v*p0 ) % self.MOD
                            ff=ee.copy()
                            ff[0]=(ynewl + v*p0 ) % self.MOD
                            g[k].append(ff)
                            #g[k].append([newl, ynewr, l0, rlen+1])
                i = (i-1)&k
            if one_num == n - num + 1:
                count_res += len(g[k])
                lm = k^((1<<(n+1)) -1)
                xlen = self.lenlist[lm]
                if lm in self.numlist:
                    aa=self.numlist[lm]
                    for x,y,_,w in g[k]:
                        # l,r, llen,rlen = info 
                        # l x r
                        #tmp = 
                        #if tmp in aa: self.res += aa[tmp]
                        self.res += aa.get((self.r - x* pow10[xlen+w] - y) * pinv[w] % self.MOD ,0)
        #print('calc time=',time.time()-t0)
[code - 验题人的py(TLE)]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
# 算法三
class Solution:
    def treeOfInfiniteSouls(self, a: List[int], p: int, r: int) -> int:
        self.MOD = p
        n = len(a)
        lnum = n//2
        rnum = n-lnum
        ways = self.sea(n) 
        res = 0 
        for way in ways:
            tmp, tidx = 0, 0
            for idx, i in enumerate(way):
                if i=='}':
                    tmp += 1
                if tmp == lnum:
                    tidx = idx
                    break
            ls, rs = way[:tidx+1], way[tidx+1:]
            for xlist in itertools.combinations(a, lnum):
                xcount = Counter(xlist)
                ylist = []
                ylen = len(rs) - rnum * 2
                for i in a:
                    if xcount[i] > 0:
                        xcount[i] -= 1
                    else:
                        ylen += len(str(i))
                        ylist.append(i)
                xtmp = pow(10, ylen, self.MOD)
                xdict = defaultdict(int)
                for new_xlist in itertools.permutations(xlist, lnum):
                    xmod = self.get_val(ls, new_xlist)
                    xval =  xmod * xtmp % self.MOD  
                    xdict[xval] += 1
                    
                for new_ylist in itertools.permutations(ylist, rnum):
                    ymod = self.get_val(rs, new_ylist)
                    yval = (r-ymod)% self.MOD
                    res += xdict[yval]
        return res

    def get_val(self, s, vlist):
        val = s.format(*vlist)
        return int(val)%self.MOD

    @cache
    def sea(self, n):
        if n==1:
            return ['1{}9']
        
        res = []
        for i in range(1,n):
            llist, rlist = self.sea(i), self.sea(n-i)
            for l in llist:
                for r in rlist:
                    res.append(f'1{l}{r}9')
        return res
[code - 暴力DP(TLE)]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=10,M=205;
int pow10[M],l[N],len[1<<N],ans;
int log10(int n){return n<10?1:log10(n/10)+1;}
class Solution {
public:
	int treeOfInfiniteSouls(vector<int>& a,int p,int r) {
		int n=a.size();
		//if (n==9)return p==90007?5762:(p==2?518918400:9);
		pow10[0]=1%p; for (int i=1;i<M;++i)pow10[i]=(ll)pow10[i-1]*10%p;
		for (int i=0;i<n;++i)l[i]=log10(a[i]);
		for (int i=1;i<(1<<n);++i){
			len[i]=(__builtin_popcount(i)*2-1)*2;
			for (int j=0;j<n;++j)if (i&(1<<j))len[i]+=l[j];
		}
		vector<int> c[1<<N];
		for (int i=0;i<n;++i)c[1<<i].push_back(((ll)a[i]*10+pow10[l[i]+1]+9)%p);
		for (int i=1;i<(1<<n);++i)
			for (int j=(i-1)&i;j;j=(j-1)&i)
				for (auto &v1:c[j]){
					ll t1=pow10[len[i]-1]+9+(ll)v1*pow10[len[i-j]+1];
					for (auto &v2:c[i-j])
						c[i].push_back(((ll)v2*10+t1)%p);
				}
		return count(c[(1<<n)-1].begin(),c[(1<<n)-1].end(),r);
	}
};
[code - 暴力dfs(TLE)]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int M=205;
int pow10[M],ans,p,r,S;
struct node{
	int v,l;
};
int log10(int n){
	int res=1;
	while (n>=10)++res,n/=10;
	return res;
}
void dfs(vector<node> &a,int minj){
	if (a.size()==1){
		if (a[0].v==r)++ans;
		++S;
		return;
	}
	for (int j=minj;j<a.size();++j)
		for (int i=0;i<j;++i){
			vector<node> a1=a;
			for (int k=i;k<j-1;++k)a1[k]=a1[k+1];
			for (int k=j-1;k<a.size()-2;++k)a1[k]=a1[k+2]; a1.pop_back();
			int l=a[i].l+a[j].l+2;
			a1[a1.size()-1]={((ll)a[i].v*pow10[a[j].l+1]+(ll)a[j].v*10+pow10[l-1]+9)%p,l};
			dfs(a1,j-1);
			a1[a1.size()-1]={((ll)a[j].v*pow10[a[i].l+1]+(ll)a[i].v*10+pow10[l-1]+9)%p,l};
			dfs(a1,j-1);
		}
}
class Solution {
public:
	int treeOfInfiniteSouls(vector<int>& a,int p,int r) {
		int n=a.size(); ans=0; ::p=p; ::r=r;
		pow10[0]=1%p; for (int i=1;i<M;++i)pow10[i]=(ll)pow10[i-1]*10%p;
		vector<node> c(n);
		for (int i=0;i<n;++i)
			c[i].l=log10(a[i])+2,c[i].v=((ll)a[i]*10+pow10[c[i].l-1]+9)%p;
		dfs(c,1);
		//printf("S=%d\n",S);
		return ans;
	}
};
 Comments
On this page
LCP 82-万灵之树
  1. 题解