0004-寻找两个正序数组的中位数
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
示例 1:
**输入:** nums1 = [1,3], nums2 = [2]
**输出:** 2.00000
**解释:** 合并数组 = [1,2,3] ,中位数 2
示例 2:
**输入:** nums1 = [1,2], nums2 = [3,4]
**输出:** 2.50000
**解释:** 合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
提示:
nums1.length == mnums2.length == n0 <= m <= 10000 <= n <= 10001 <= m + n <= 2000-106 <= nums1[i], nums2[i] <= 106
解法一
简单粗暴,先将两个数组合并,两个有序数组的合并也是归并排序中的一部分。然后根据奇数,还是偶数,返回中位数。
代码
1 | public double findMedianSortedArrays(int[] nums1, int[] nums2) { |
时间复杂度:遍历全部数组 $(m+n)$
空间复杂度:开辟了一个数组,保存合并后的两个数组 $O(m+n)$
解法二
其实,我们不需要将两个数组真的合并,我们只需要找到中位数在哪里就可以了。
开始的思路是写一个循环,然后里边判断是否到了中位数的位置,到了就返回结果,但这里对偶数和奇数的分类会很麻烦。当其中一个数组遍历完后,出了 for 循环对边界的判断也会分几种情况。总体来说,虽然复杂度不影响,但代码会看起来很乱。
首先是怎么将奇数和偶数的情况合并一下。
用 len 表示合并后数组的长度,如果是奇数,我们需要知道第 (len+1)/2 个数就可以了,如果遍历的话需要遍历 int(len/2 ) + 1 次。如果是偶数,我们需要知道第 len/2和 len/2+1 个数,也是需要遍历 len/2+1 次。所以遍历的话,奇数和偶数都是 len/2+1 次。
返回中位数的话,奇数需要最后一次遍历的结果就可以了,偶数需要最后一次和上一次遍历的结果。所以我们用两个变量 left 和 right,right 保存当前循环的结果,在每次循环前将 right 的值赋给 left。这样在最后一次循环的时候,left 将得到 right 的值,也就是上一次循环的结果,接下来 right 更新为最后一次的结果。
循环中该怎么写,什么时候 A 数组后移,什么时候 B 数组后移。用 aStart 和 bStart 分别表示当前指向 A 数组和 B 数组的位置。如果 aStart 还没有到最后并且此时 A 位置的数字小于 B 位置的数组,那么就可以后移了。也就是aStart<m&&A[aStart]< B[bStart]。
但如果 B 数组此刻已经没有数字了,继续取数字 B[ bStart ],则会越界,所以判断下 bStart 是否大于数组长度了,这样 || 后边的就不会执行了,也就不会导致错误了,所以增加为 aStart<m&&(bStart) >= n||A[aStart]<B[bStart]) 。
代码
1 | public double findMedianSortedArrays(int[] A, int[] B) { |
时间复杂度:遍历 len/2+1 次,len=m+n,所以时间复杂度依旧是 $O(m+n)$。
空间复杂度:我们申请了常数个变量,也就是 m,n,len,left,right,aStart,bStart 以及 i。
总共 8 个变量,所以空间复杂度是 $O(1)$。
解法三
上边的两种思路,时间复杂度都达不到题目的要求 $O(log(m+n)$。看到 log,很明显,我们只有用到二分的方法才能达到。我们不妨用另一种思路,题目是求中位数,其实就是求第 k 小数的一种特殊情况,而求第 k 小数有一种算法。
解法二中,我们一次遍历就相当于去掉不可能是中位数的一个值,也就是一个一个排除。由于数列是有序的,其实我们完全可以一半儿一半儿的排除。假设我们要找第 k 小数,我们可以每次循环排除掉 k/2 个数。看下边一个例子。
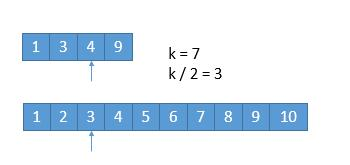
假设我们要找第 7 小的数字。
 {:width=500}
{:width=500}
{:align=center}
我们比较两个数组的第 k/2 个数字,如果 k 是奇数,向下取整。也就是比较第 $3$ 个数字,上边数组中的 $4$ 和下边数组中的 $3$,如果哪个小,就表明该数组的前 k/2 个数字都不是第 k 小数字,所以可以排除。也就是 $1$,$2$,$3$ 这三个数字不可能是第 $7$ 小的数字,我们可以把它排除掉。将 $1349$ 和 $45678910$ 两个数组作为新的数组进行比较。
更一般的情况 A[1] ,A[2] ,A[3],A[k/2] … ,B[1],B[2],B[3],B[k/2] … ,如果 A[k/2]<B[k/2] ,那么A[1],A[2],A[3],A[k/2]都不可能是第 k 小的数字。
A 数组中比 A[k/2] 小的数有 k/2-1 个,B 数组中,B[k/2] 比 A[k/2] 小,假设 B[k/2] 前边的数字都比 A[k/2] 小,也只有 k/2-1 个,所以比 A[k/2] 小的数字最多有 k/1-1+k/2-1=k-2个,所以 A[k/2] 最多是第 k-1 小的数。而比 A[k/2] 小的数更不可能是第 k 小的数了,所以可以把它们排除。
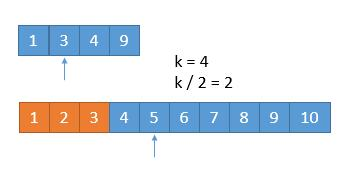
橙色的部分表示已经去掉的数字。
 {:width=500}
{:width=500}
{:align=center}
由于我们已经排除掉了 3 个数字,就是这 3 个数字一定在最前边,所以在两个新数组中,我们只需要找第 7 - 3 = 4 小的数字就可以了,也就是 k = 4。此时两个数组,比较第 2 个数字,3 < 5,所以我们可以把小的那个数组中的 1 ,3 排除掉了。
 {:width=500}
{:width=500}
{:align=center}
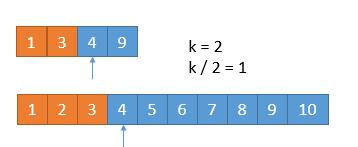
我们又排除掉 2 个数字,所以现在找第 4 - 2 = 2 小的数字就可以了。此时比较两个数组中的第 k / 2 = 1 个数,4 == 4,怎么办呢?由于两个数相等,所以我们无论去掉哪个数组中的都行,因为去掉 1 个总会保留 1 个的,所以没有影响。为了统一,我们就假设 4 > 4 吧,所以此时将下边的 4 去掉。
 {:width=500}
{:width=500}
{:align=center}
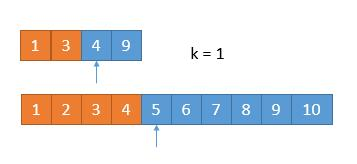
由于又去掉 1 个数字,此时我们要找第 1 小的数字,所以只需判断两个数组中第一个数字哪个小就可以了,也就是 4。
所以第 7 小的数字是 4。
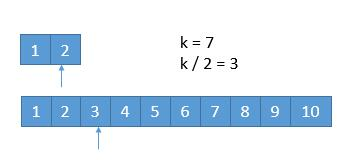
我们每次都是取 k/2 的数进行比较,有时候可能会遇到数组长度小于 k/2的时候。
 {:width=500}
{:width=500}
{:align=center}
此时 k / 2 等于 3,而上边的数组长度是 2,我们此时将箭头指向它的末尾就可以了。这样的话,由于 2 < 3,所以就会导致上边的数组 1,2 都被排除。造成下边的情况。
 {:width=500}
{:width=500}
{:align=center}
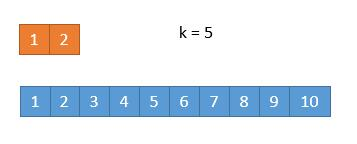
由于 2 个元素被排除,所以此时 k = 5,又由于上边的数组已经空了,我们只需要返回下边的数组的第 5 个数字就可以了。
从上边可以看到,无论是找第奇数个还是第偶数个数字,对我们的算法并没有影响,而且在算法进行中,k 的值都有可能从奇数变为偶数,最终都会变为 1 或者由于一个数组空了,直接返回结果。
所以我们采用递归的思路,为了防止数组长度小于 k/2,所以每次比较 min(k/2,len(数组) 对应的数字,把小的那个对应的数组的数字排除,将两个新数组进入递归,并且 k 要减去排除的数字的个数。递归出口就是当 k=1 或者其中一个数字长度是 0 了。
代码
1 | public double findMedianSortedArrays(int[] nums1, int[] nums2) { |
时间复杂度:每进行一次循环,我们就减少 k/2 个元素,所以时间复杂度是 O(log(k),而 k=(m+n)/2,所以最终的复杂也就是 $O(log(m+n)$。
空间复杂度:虽然我们用到了递归,但是可以看到这个递归属于尾递归,所以编译器不需要不停地堆栈,所以空间复杂度为 $O(1)$。
解法四
我们首先理一下中位数的定义是什么
中位数(又称中值,英语:Median),[统计学] (https://baike.baidu.com/item/%E7%BB%9F%E8%AE%A1%E5%AD%A6/2630438)中的专有名词,代表一个样本、种群或 [概率分布] (https://baike.baidu.com/item/%E6%A6%82%E7%8E%87%E5%88%86%E5%B8%83/828907)中的一个数值,其可将数值集合划分为相等的上下两部分。
所以我们只需要将数组进行切。
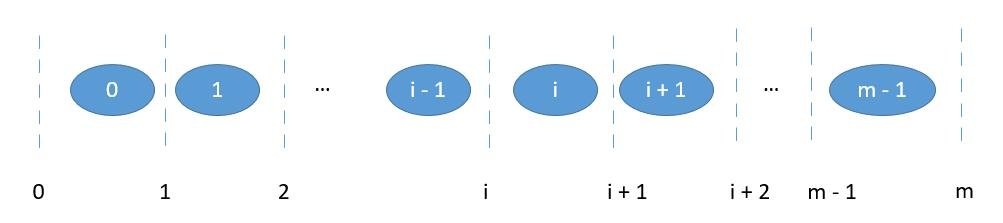
一个长度为 m 的数组,有 0 到 m 总共 m + 1 个位置可以切。
 {:width=500}
{:width=500}
{:align=center}
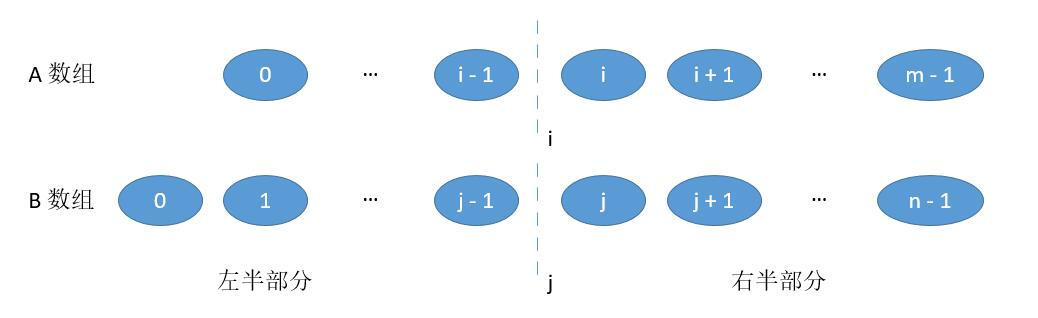
我们把数组 A 和数组 B 分别在 i 和 j 进行切割。
 {:width=500}
{:width=500}
{:align=center}
将 i 的左边和 j 的左边组合成「左半部分」,将 i 的右边和 j 的右边组合成「右半部分」。
当 A 数组和 B 数组的总长度是偶数时,如果我们能够保证
*左半部分的长度等于右半部分
i + j = m - i + n - j , 也就是 j = ( m + n ) / 2 - i*左半部分最大的值小于等于右半部分最小的值 max ( A [ i - 1 ] , B [ j - 1 ])) <= min ( A [ i ] , B [ j ]))
那么,中位数就可以表示如下 (左半部分最大值 + 右半部分最小值 )/ 2。 (max ( A [ i - 1 ] , B [ j - 1 ])+ min ( A [ i ] , B [ j ])) / 2当 A 数组和 B 数组的总长度是奇数时,如果我们能够保证
*左半部分的长度比右半部分大 1
i + j = m - i + n - j + 1也就是 j = ( m + n + 1) / 2 - i*左半部分最大的值小于等于右半部分最小的值 max ( A [ i - 1 ] , B [ j - 1 ])) <= min ( A [ i ] , B [ j ]))
那么,中位数就是 左半部分最大值,也就是左半部比右半部分多出的那一个数。 max ( A [ i - 1 ] , B [ j - 1 ])
上边的第一个条件我们其实可以合并为 $j = ( m + n + 1) / 2 - i$,因为如果 $m + n$ 是偶数,由于我们取的是 $int$ 值,所以加 $1$ 也不会影响结果。当然,由于 $0 <= i <= m$ ,为了保证 $0 <= j <= n$,我们必须保证 $m <= n$。
$$ m\leq n,i<m,j=(m+n+1)/2-i\geq(m+m+1)/2-i>(m+m+1)/2-m=0 $$
$$ m\leq n,i>0,j=(m+n+1)/2-i\leq (n+n+1)/2-i<(n+n+1)/2=n $$
最后一步由于是 int 间的运算,所以 $1/2=0$。
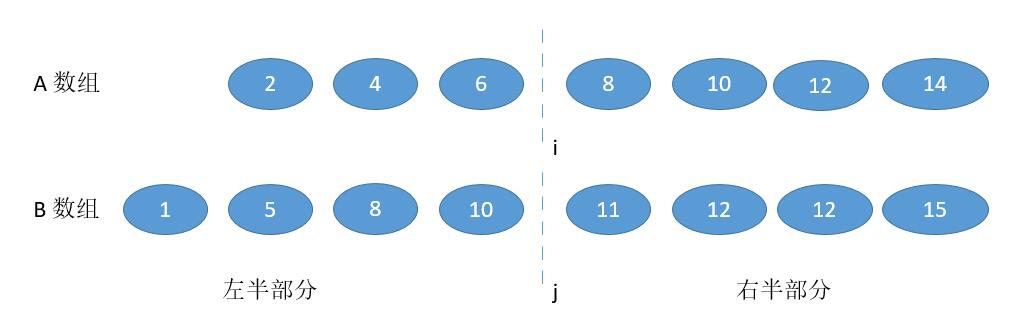
而对于第二个条件,奇数和偶数的情况是一样的,我们进一步分析。为了保证 max ( A [ i - 1 ] , B [ j - 1 ])) <= min ( A [ i ] , B [ j ])),因为 A 数组和 B 数组是有序的,所以 A [ i - 1 ] <= A [ i ],B [ i - 1 ] <= B [ i ] 这是天然的,所以我们只需要保证 B [ j - 1 ] < = A [ i ] 和 A [ i - 1 ] <= B [ j ] 所以我们分两种情况讨论:
- B [ j - 1 ] > A [ i ],并且为了不越界,要保证 j != 0,i != m
 {:width=500}
{:width=500}
{:align=center}
此时很明显,我们需要增加 i ,为了数量的平衡还要减少 j ,幸运的是 j = ( m + n + 1) / 2 - i,i 增大,j 自然会减少。
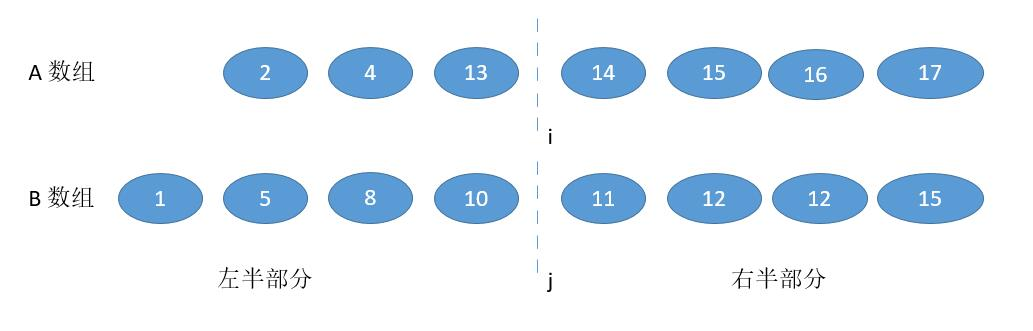
- A [ i - 1 ] > B [ j ] ,并且为了不越界,要保证 i != 0,j != n
 {:width=500}
{:width=500}
{:align=center}
此时和上边的情况相反,我们要减少 i ,增大 j 。
上边两种情况,我们把边界都排除了,需要单独讨论。
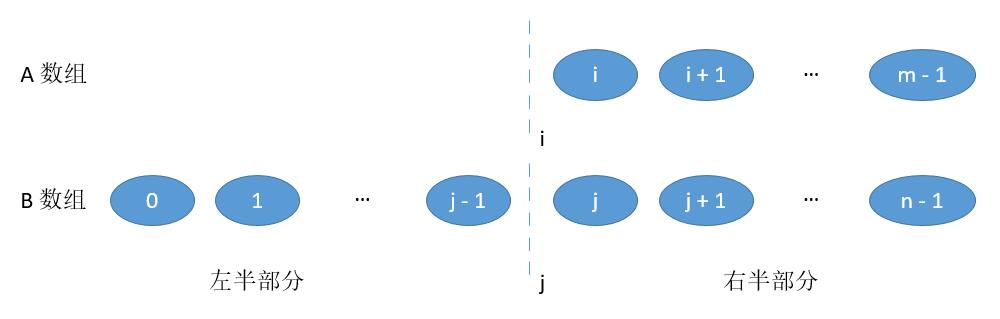
- 当 i = 0, 或者 j = 0,也就是切在了最前边。
 {:width=500}
{:width=500}
{:align=center}
此时左半部分当 j = 0 时,最大的值就是 A [ i - 1 ] ;当 i = 0 时 最大的值就是 B [ j - 1] 。右半部分最小值和之前一样。
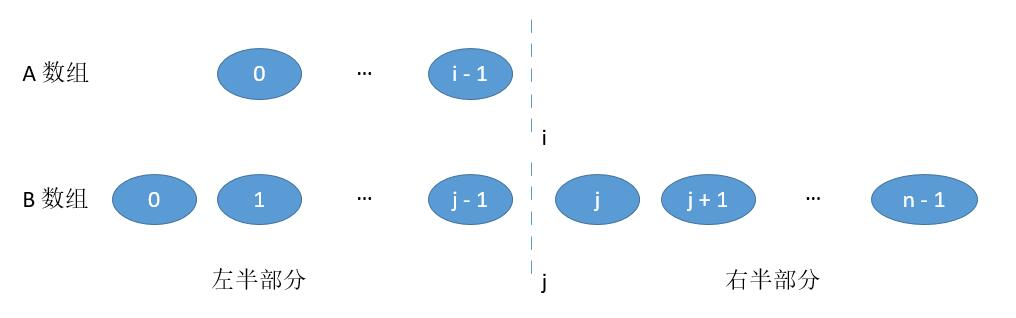
- 当 i = m 或者 j = n,也就是切在了最后边。
 {:width=500}
{:width=500}
{:align=center}
此时左半部分最大值和之前一样。右半部分当 j = n 时,最小值就是 A [ i ] ;当 i = m 时,最小值就是B [ j ] 。
所有的思路都理清了,最后一个问题,增加 i 的方式。当然用二分了。初始化 i 为中间的值,然后减半找中间的,减半找中间的,减半找中间的直到答案。
1 | class Solution { |
时间复杂度:我们对较短的数组进行了二分查找,所以时间复杂度是 $O(log(min(m,n))$。
空间复杂度:只有一些固定的变量,和数组长度无关,所以空间复杂度是 $O ( 1 )$。
总结
解法二中体会到了对情况的转换,有时候即使有了思路,代码也不一定写的优雅,需要多锻炼才可以。解法三和解法四充分发挥了二分查找的优势,将时间复杂度降为 log 级别。