0011-盛最多水的容器

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 10:40:28 2023-09-13 10:40:28 Updated    

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明： 你不能倾斜容器。

示例 1：

![](https://aliyun-lc-upload.oss-cn-hangzhou.aliyuncs.com/aliyun-lc-
upload/uploads/2018/07/25/question_11.jpg)

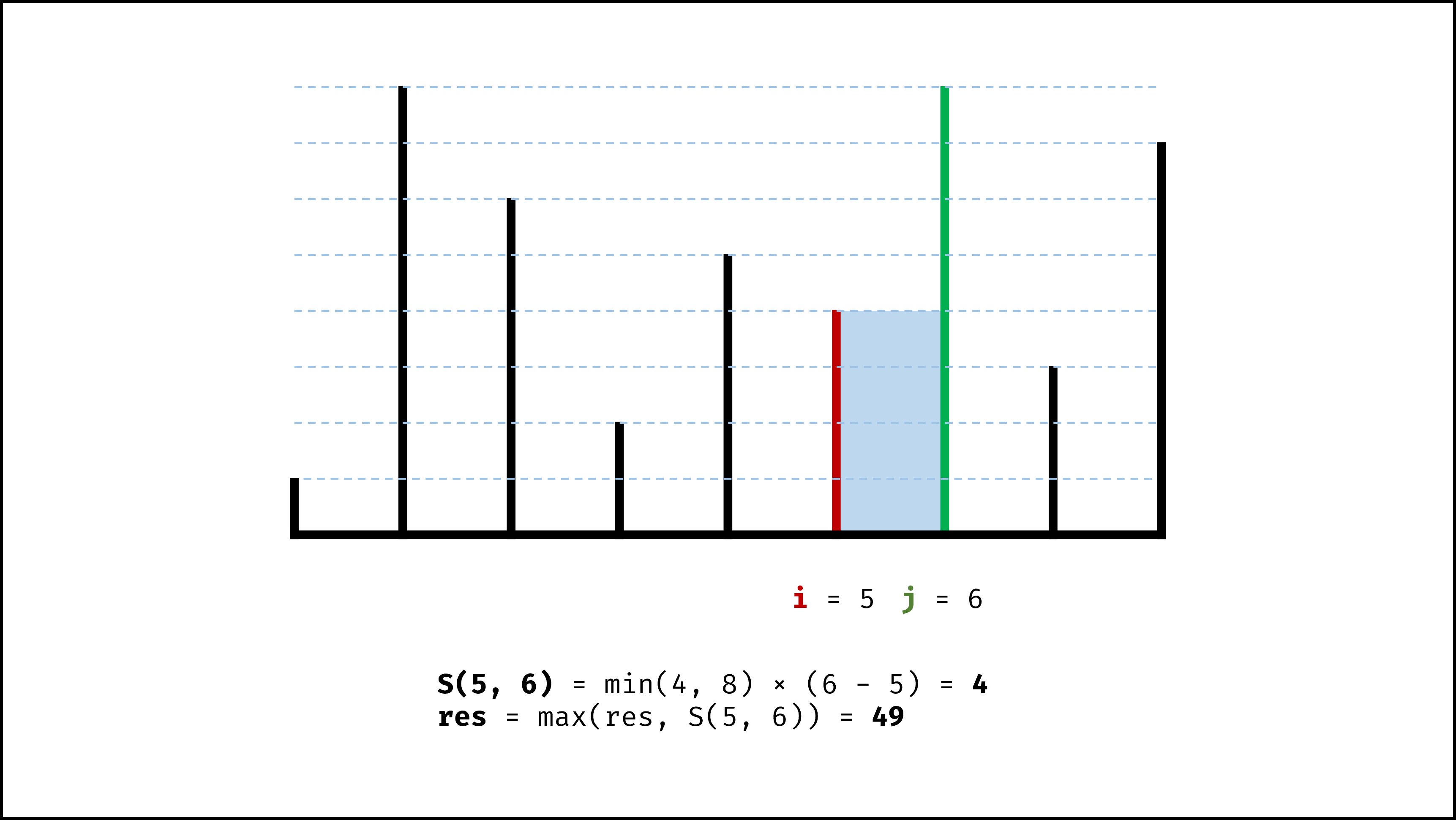
**输入：** [1,8,6,2,5,4,8,3,7]
**输出：** 49 
**解释：** 图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

**输入：** height = [1,1]
**输出：** 1

提示：

  • n == height.length
  • 2 <= n <= 105
  • 0 <= height[i] <= 104

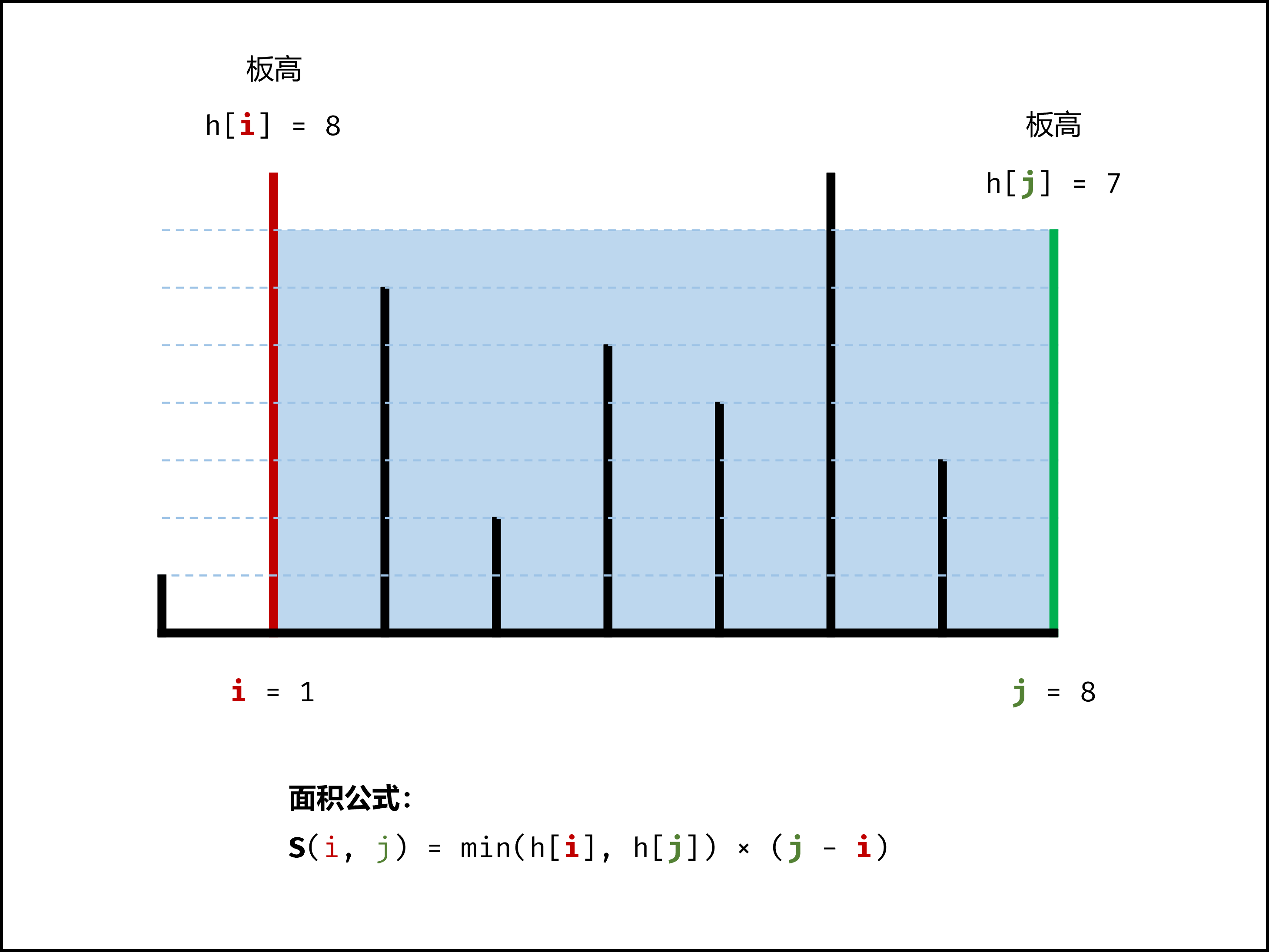
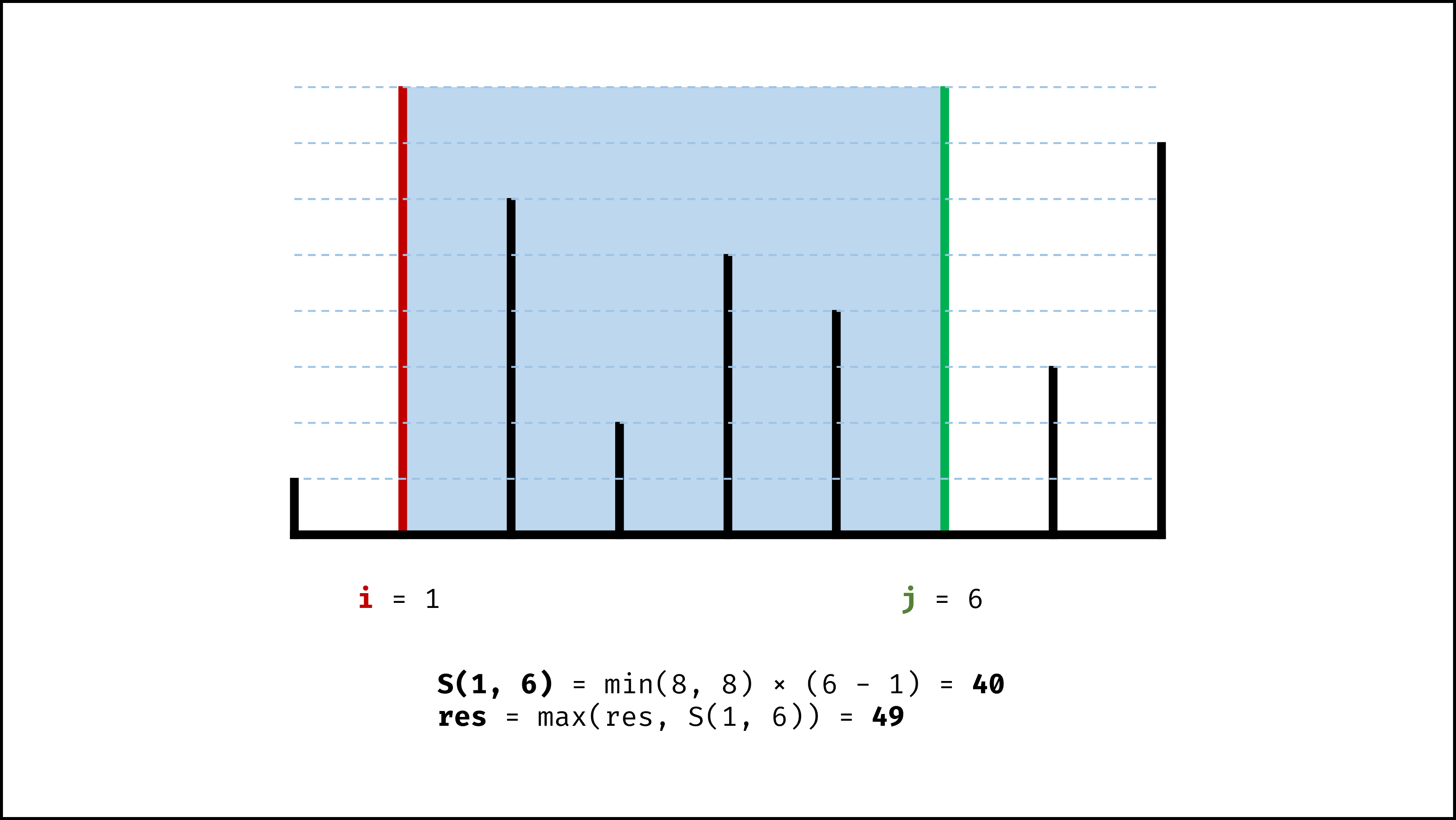
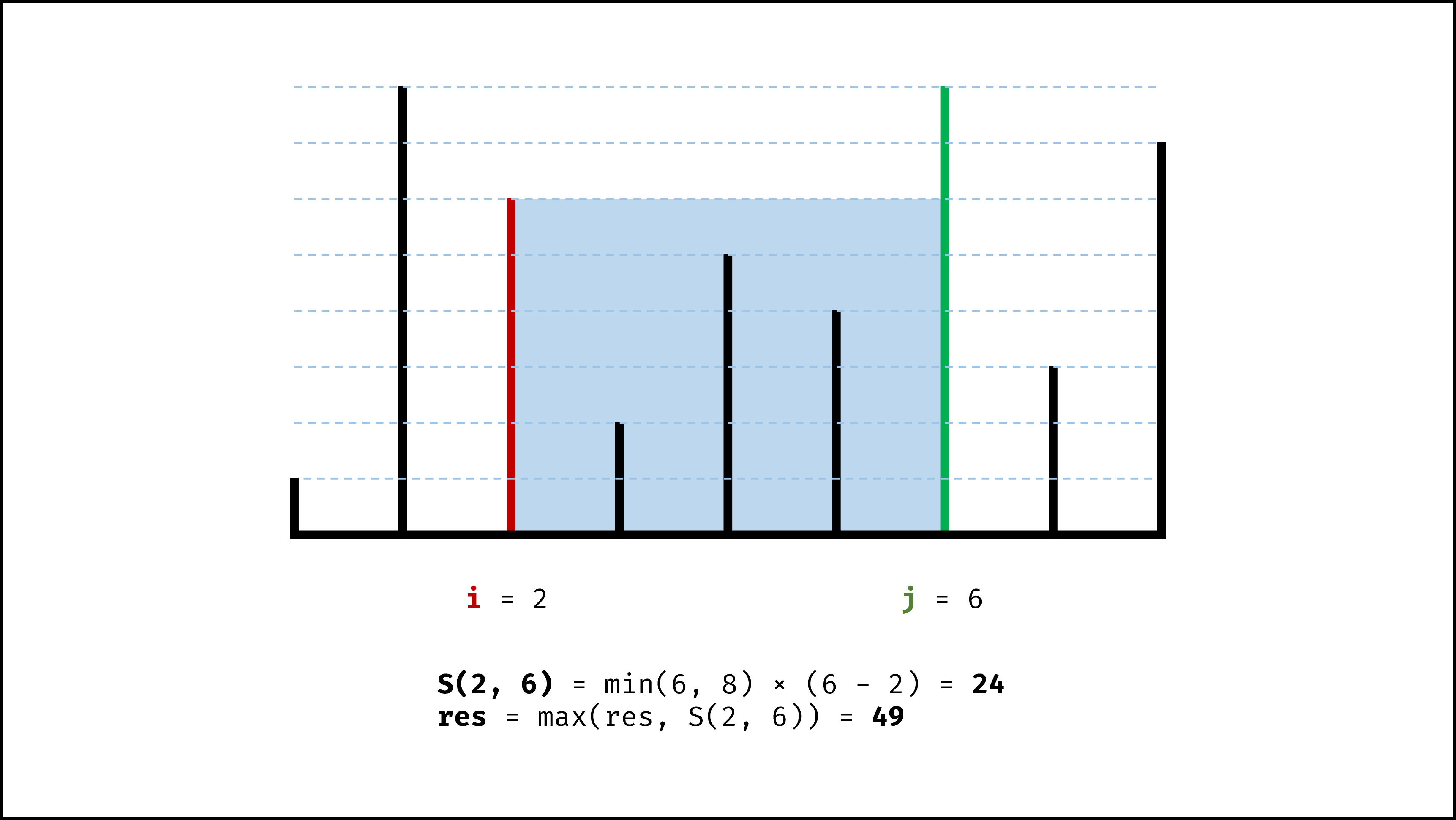
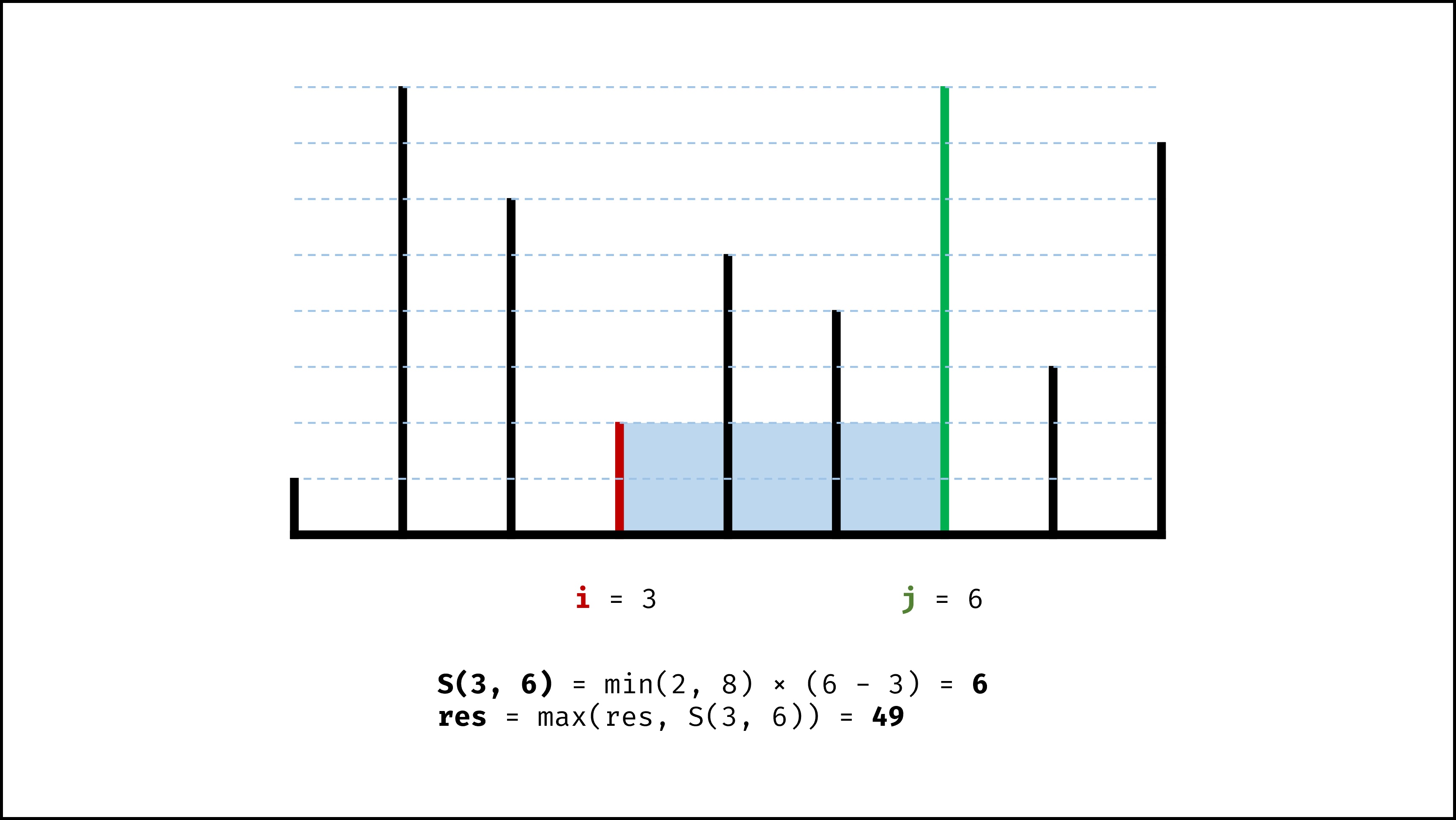
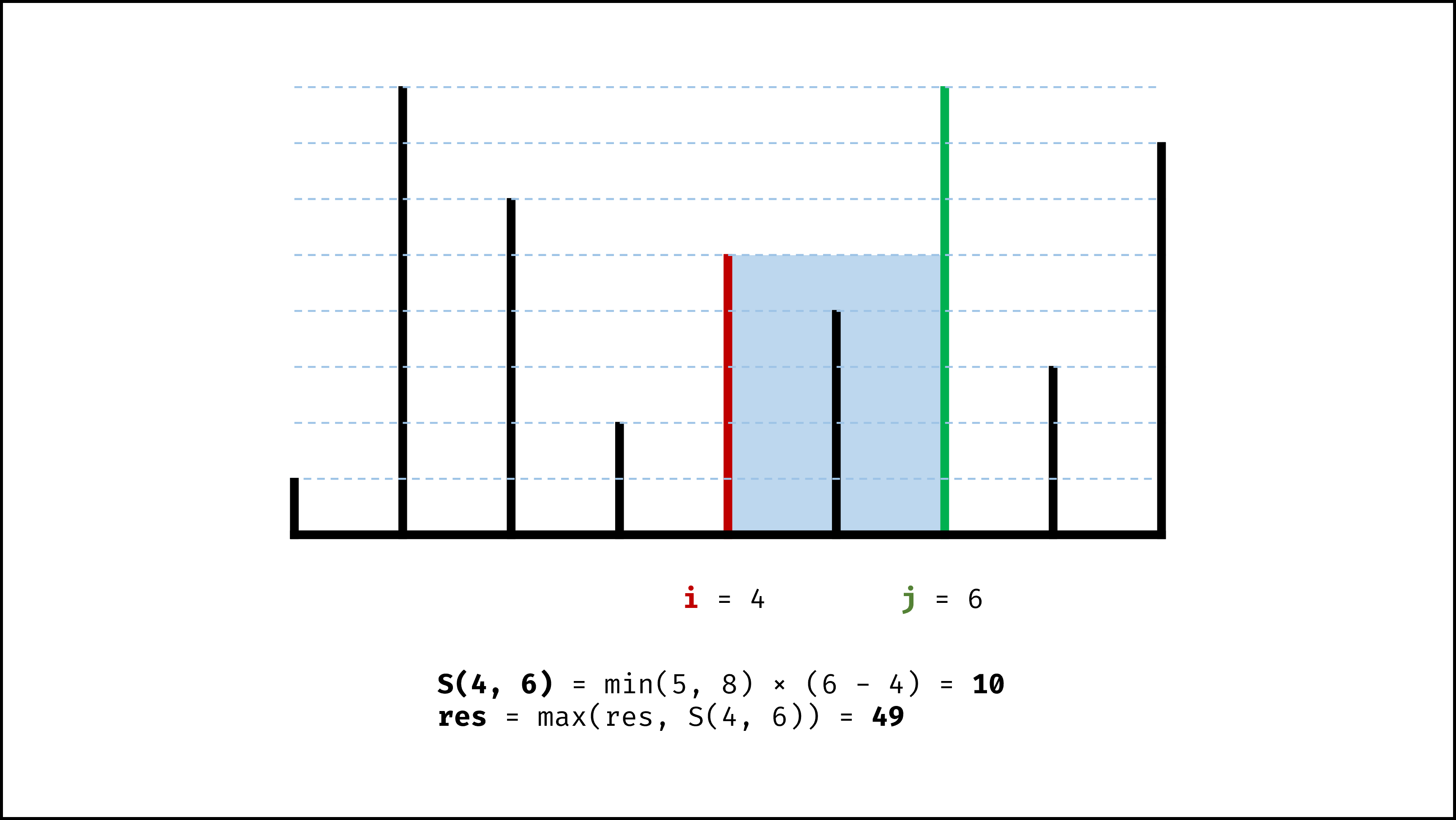
设两指针 $i$ , $j$ ，指向的水槽板高度分别为 $h[i]$ , $h[j]$ ，此状态下水槽面积为 $S(i, j)$ 。由于可容纳水的高度由两板中的 短板 决定，因此可得如下 面积公式 ：

$$
S(i, j) = min(h[i], h[j]) × (j - i)
$$

Picture0.png{:width=500}

在每个状态下，无论长板或短板向中间收窄一格，都会导致水槽 底边宽度 $-1$​ 变短：

  • 若向内 移动短板 ，水槽的短板 $min(h[i], h[j])$ 可能变大，因此下个水槽的面积 可能增大 。
  • 若向内 移动长板 ，水槽的短板 $min(h[i], h[j])$​ 不变或变小，因此下个水槽的面积 一定变小 。

因此，初始化双指针分列水槽左右两端，循环每轮将短板向内移动一格，并更新面积最大值，直到两指针相遇时跳出；即可获得最大面积。

算法流程：

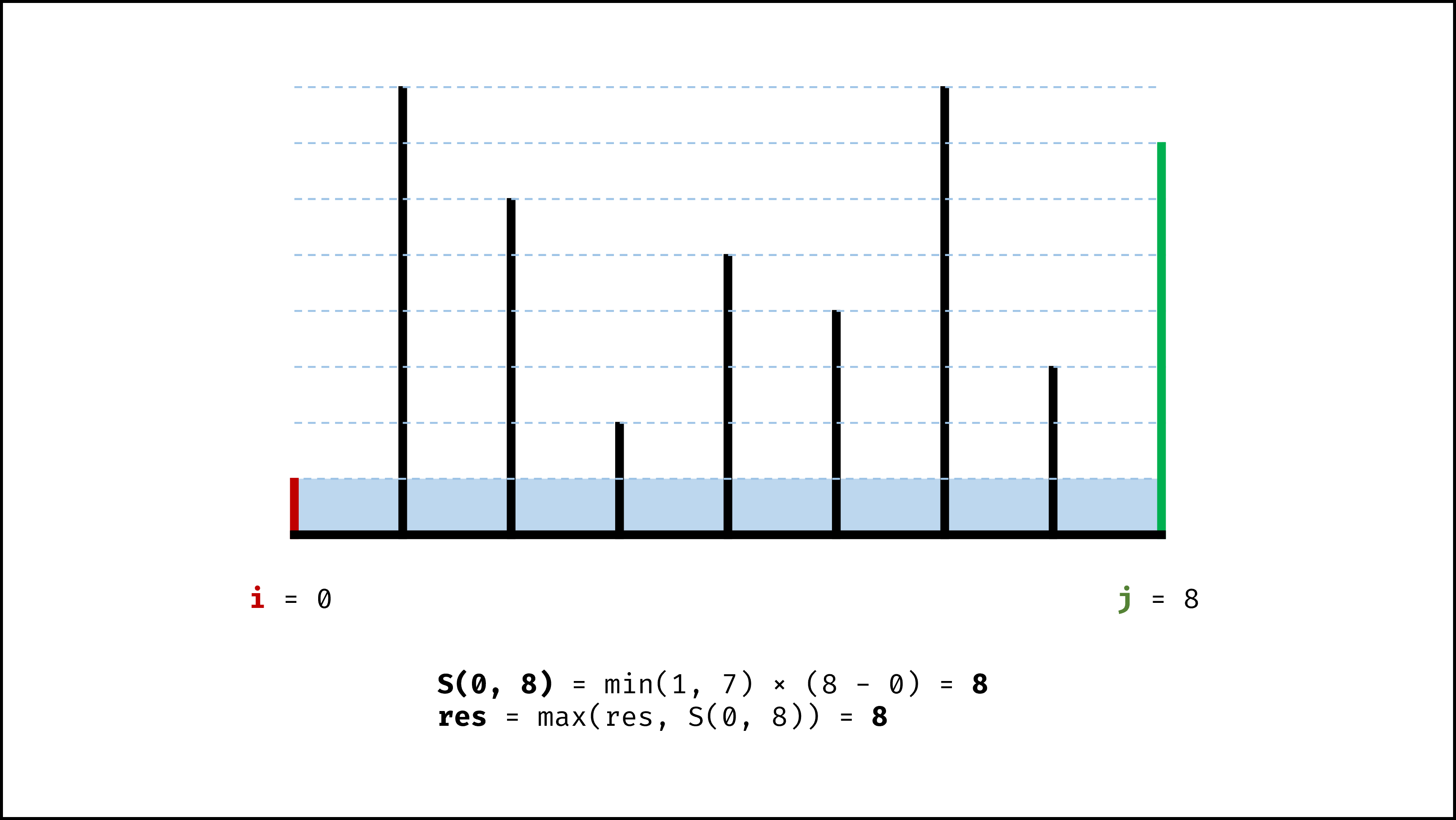
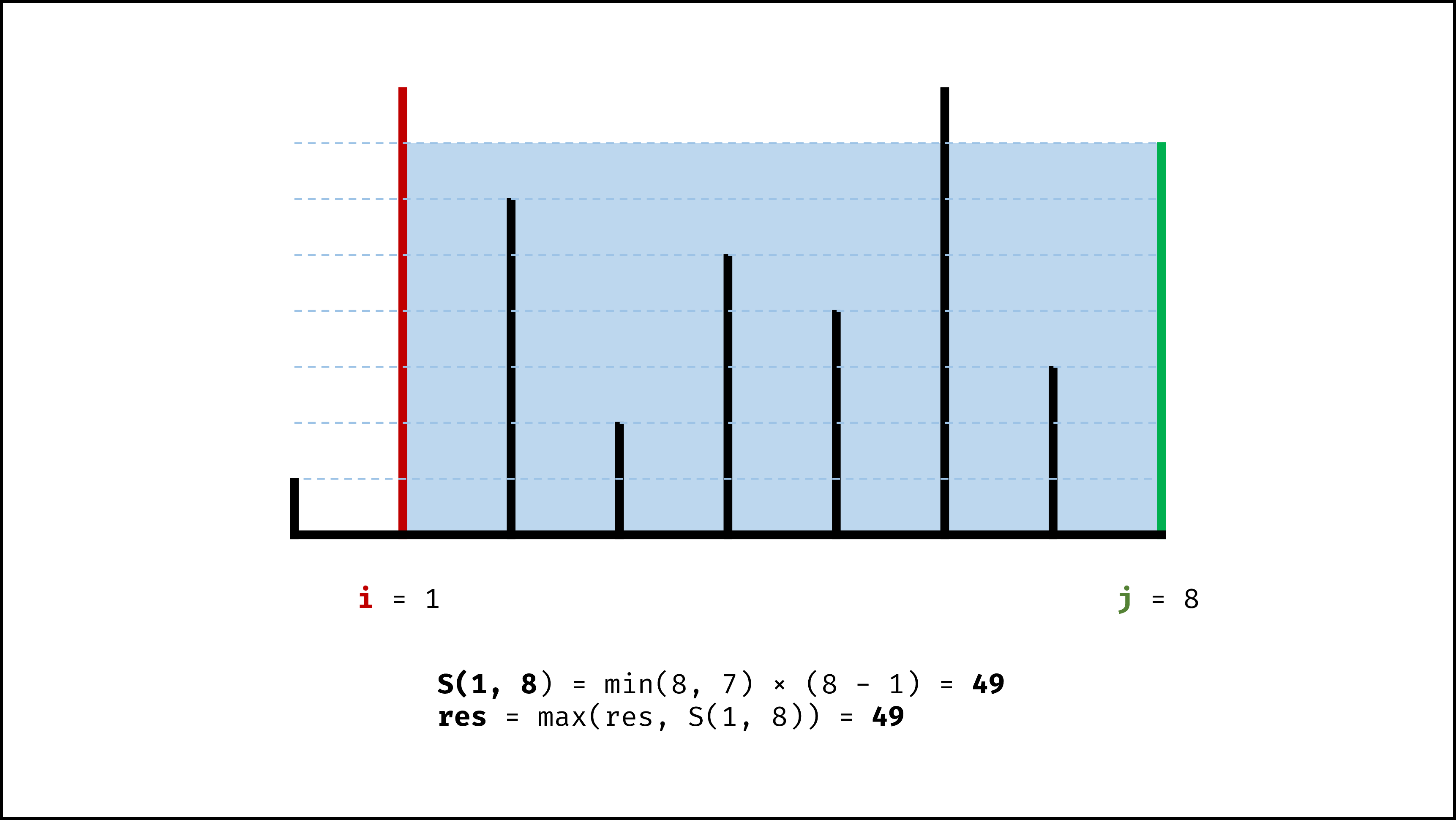
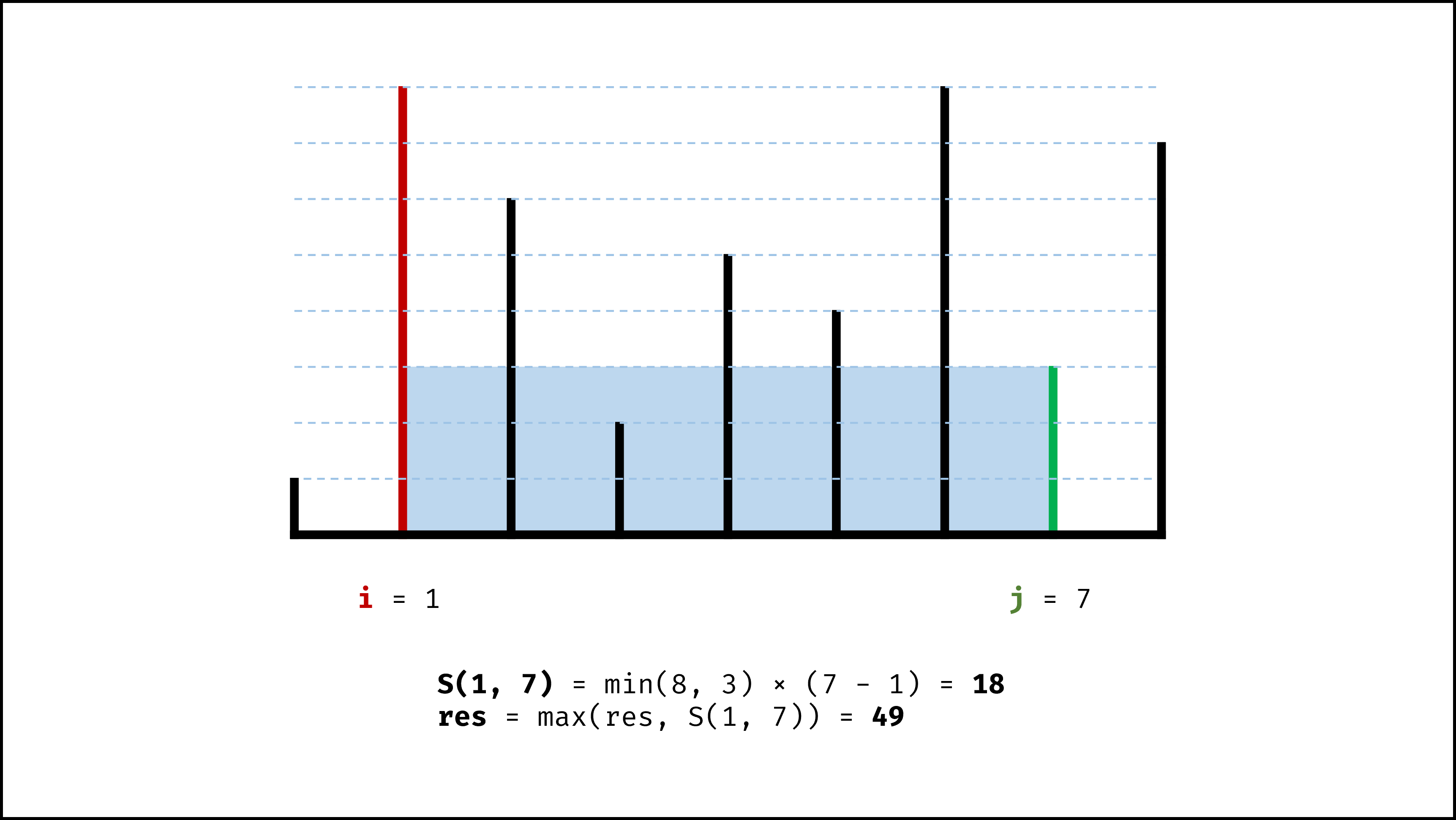
  1. 初始化： 双指针 $i$ , $j$ 分列水槽左右两端；
  2. 循环收窄： 直至双指针相遇时跳出；
    1. 更新面积最大值 $res$ ；
    2. 选定两板高度中的短板，向中间收窄一格；
  3. 返回值： 返回面积最大值 $res$ 即可；

正确性证明：

若暴力枚举，水槽两板围成面积 $S(i, j)$ 的状态总数为 $C(n, 2)$ 。

假设状态 $S(i, j)$ 下 $h[i] < h[j]$ ，在向内移动短板至 $S(i + 1, j)$ ，则相当于消去了 ${S(i, j - 1), S(i, j - 2), … , S(i, i + 1)}$ 状态集合。而所有消去状态的面积一定都小于当前面积（即 $< S(i, j)$），因为这些状态：

  • 短板高度：相比 $S(i, j)$ 相同或更短（即 $\leq h[i]$ ）；
  • 底边宽度：相比 $S(i, j)$ 更短；

因此，每轮向内移动短板，所有消去的状态都 不会导致面积最大值丢失 ，证毕。

<Picture1.png,Picture2.png,Picture3.png,Picture4.png,Picture5.png,Picture6.png,Picture7.png,Picture8.png>

复杂度分析：

  • 时间复杂度 $O(N)$​ ： 双指针遍历一次底边宽度 $N$​​ 。
  • 空间复杂度 $O(1)$​ ： 变量 $i$ , $j$ , $res$ 使用常数额外空间。

代码：

[]
1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def maxArea(self, height: List[int]) -> int:
        i, j, res = 0, len(height) - 1, 0
        while i < j:
            if height[i] < height[j]:
                res = max(res, height[i] * (j - i))
                i += 1
            else:
                res = max(res, height[j] * (j - i))
                j -= 1
        return res
[]
1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public int maxArea(int[] height) {
        int i = 0, j = height.length - 1, res = 0;
        while(i < j) {
            res = height[i] < height[j] ? 
                Math.max(res, (j - i) * height[i++]): 
                Math.max(res, (j - i) * height[j--]); 
        }
        return res;
    }
}
[]
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int maxArea(vector<int>& height) {
        int i = 0, j = height.size() - 1, res = 0;
        while(i < j) {
            res = height[i] < height[j] ? 
                max(res, (j - i) * height[i++]): 
                max(res, (j - i) * height[j--]); 
        }
        return res;
    }
};

link

本学习计划配有代码仓，内含测试样例与数据结构封装，便于本地调试。可前往我的个人主页 获取。

 Comments
On this page
0011-盛最多水的容器