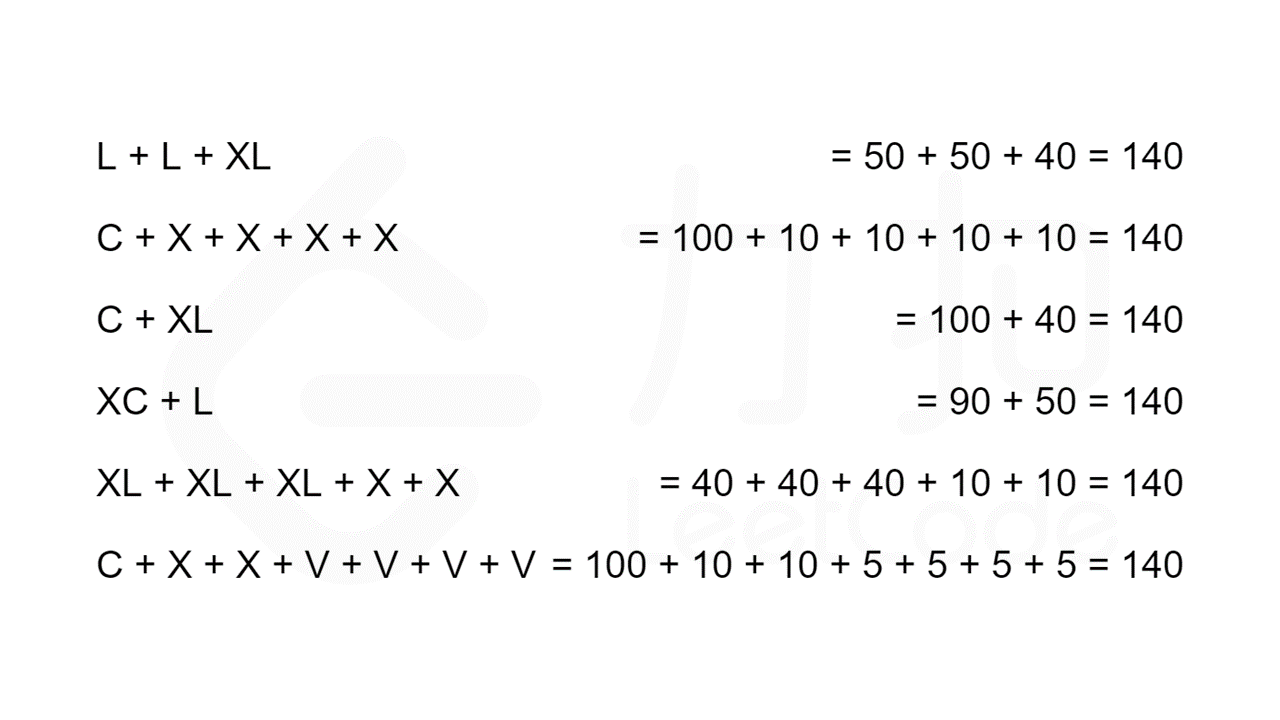罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。
**字符** **数值**
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
例如, 罗马数字 2 写做 II ,即为两个并列的 1。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为XX + V + II 。
通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5IX。这个特殊的规则只适用于以下六种情况:
I 可以放在 V (5) 和 X (10) 的左边,来表示 4 和 9。X 可以放在 L (50) 和 C (100) 的左边,来表示 40 和 90。 C 可以放在 D (500) 和 M (1000) 的左边,来表示 400 和 900。
给你一个整数,将其转为罗马数字。
示例 1:
**输入:** num = 3
**输出:** "III"
示例 2:
**输入:** num = 4
**输出:** "IV"
示例 3:
**输入:** num = 9
**输出:** "IX"
示例 4:
**输入:** num = 58
**输出:** "LVIII"
**解释:** L = 50, V = 5, III = 3.
示例 5:
**输入:** num = 1994
**输出:** "MCMXCIV"
**解释:** M = 1000, CM = 900, XC = 90, IV = 4.
提示:
前言 罗马数字符号
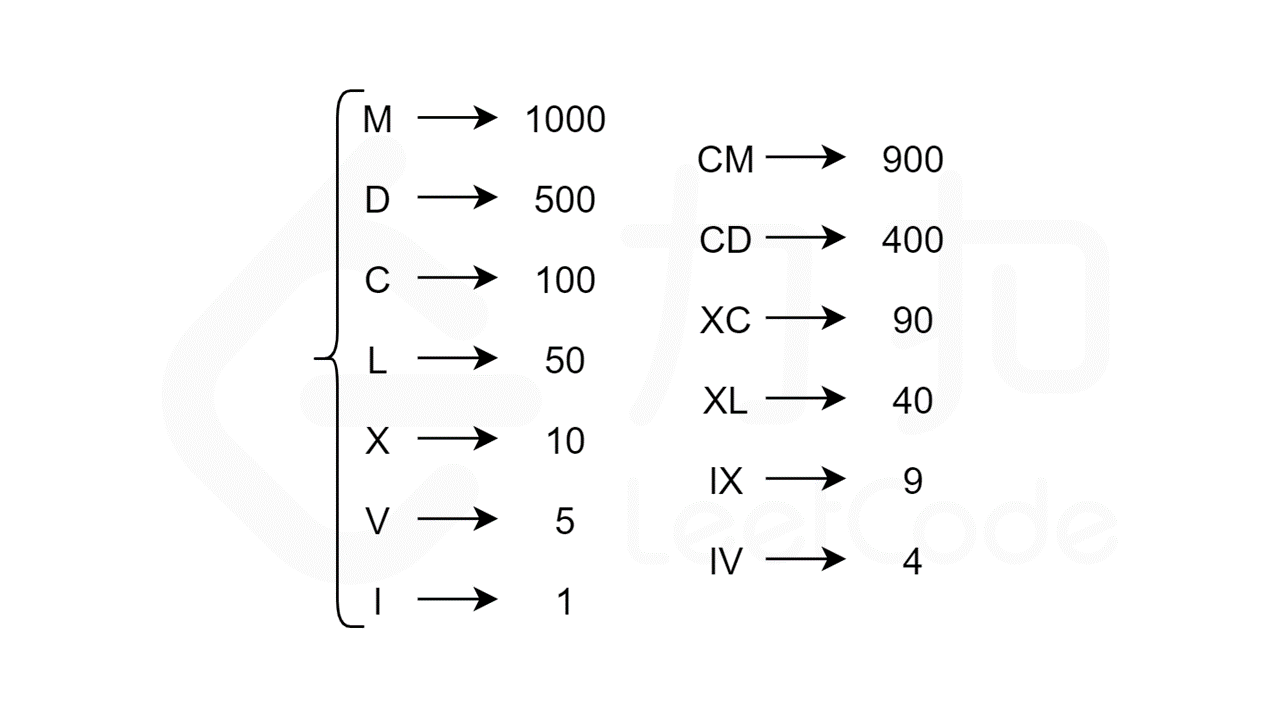
罗马数字由 $7$ 个不同的单字母符号组成,每个符号对应一个具体的数值。此外,减法规则(如问题描述中所述)给出了额外的 $6$ 个复合符号。这给了我们总共 $13$ 个独特的符号(每个符号由 $1$ 个或 $2$ 个字母组成),如下图所示。
罗马数字的唯一表示法
让我们从一个例子入手。考虑 $140$ 的罗马数字表示,下面哪一个是正确的?
我们用来确定罗马数字的规则是:对于罗马数字从左到右的每一位,选择尽可能大的符号值。对于 $140$,最大可以选择的符号值为 $\texttt{C}=100$。接下来,对于剩余的数字 $40$,最大可以选择的符号值为 $\texttt{XL}=40$。因此,$140$ 的对应的罗马数字为 $\texttt{C}+\texttt{XL}=\texttt{CXL}$。
方法一:模拟 思路
根据罗马数字的唯一表示法,为了表示一个给定的整数 $\textit{num}$,我们寻找不超过 $\textit{num}$ 的最大符号值,将 $\textit{num}$ 减去该符号值,然后继续寻找不超过 $\textit{num}$ 的最大符号值,将该符号拼接在上一个找到的符号之后,循环直至 $\textit{num}$ 为 $0$。最后得到的字符串即为 $\textit{num}$ 的罗马数字表示。
编程时,可以建立一个数值-符号对的列表 $\textit{valueSymbols}$,按数值从大到小排列。遍历 $\textit{valueSymbols}$ 中的每个数值-符号对,若当前数值 $\textit{value}$ 不超过 $\textit{num}$,则从 $\textit{num}$ 中不断减去 $\textit{value}$,直至 $\textit{num}$ 小于 $\textit{value}$,然后遍历下一个数值-符号对。若遍历中 $\textit{num}$ 为 $0$ 则跳出循环。
代码
[sol1-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 const pair<int , string> valueSymbols[] = { {1000 , "M" }, {900 , "CM" }, {500 , "D" }, {400 , "CD" }, {100 , "C" }, {90 , "XC" }, {50 , "L" }, {40 , "XL" }, {10 , "X" }, {9 , "IX" }, {5 , "V" }, {4 , "IV" }, {1 , "I" }, }; class Solution {public : string intToRoman (int num) { string roman; for (const auto &[value, symbol] : valueSymbols) { while (num >= value) { num -= value; roman += symbol; } if (num == 0 ) { break ; } } return roman; } };
[sol1-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution { int [] values = {1000 , 900 , 500 , 400 , 100 , 90 , 50 , 40 , 10 , 9 , 5 , 4 , 1 }; String[] symbols = {"M" , "CM" , "D" , "CD" , "C" , "XC" , "L" , "XL" , "X" , "IX" , "V" , "IV" , "I" }; public String intToRoman (int num) { StringBuffer roman = new StringBuffer (); for (int i = 0 ; i < values.length; ++i) { int value = values[i]; String symbol = symbols[i]; while (num >= value) { num -= value; roman.append(symbol); } if (num == 0 ) { break ; } } return roman.toString(); } }
[sol1-C#] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 public class Solution { readonly Tuple<int , string >[] valueSymbols = { new Tuple<int , string >(1000 , "M" ), new Tuple<int , string >(900 , "CM" ), new Tuple<int , string >(500 , "D" ), new Tuple<int , string >(400 , "CD" ), new Tuple<int , string >(100 , "C" ), new Tuple<int , string >(90 , "XC" ), new Tuple<int , string >(50 , "L" ), new Tuple<int , string >(40 , "XL" ), new Tuple<int , string >(10 , "X" ), new Tuple<int , string >(9 , "IX" ), new Tuple<int , string >(5 , "V" ), new Tuple<int , string >(4 , "IV" ), new Tuple<int , string >(1 , "I" ) }; public string IntToRoman (int num StringBuilder roman = new StringBuilder(); foreach (Tuple<int , string > tuple in valueSymbols) { int value = tuple.Item1; string symbol = tuple.Item2; while (num >= value ) { num -= value ; roman.Append(symbol); } if (num == 0 ) { break ; } } return roman.ToString(); } }
[sol1-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 var valueSymbols = []struct { value int symbol string }{ {1000 , "M" }, {900 , "CM" }, {500 , "D" }, {400 , "CD" }, {100 , "C" }, {90 , "XC" }, {50 , "L" }, {40 , "XL" }, {10 , "X" }, {9 , "IX" }, {5 , "V" }, {4 , "IV" }, {1 , "I" }, } func intToRoman (num int ) string { roman := []byte {} for _, vs := range valueSymbols { for num >= vs.value { num -= vs.value roman = append (roman, vs.symbol...) } if num == 0 { break } } return string (roman) }
[sol1-JavaScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 var intToRoman = function (num ) { const valueSymbols = [[1000 , "M" ], [900 , "CM" ], [500 , "D" ], [400 , "CD" ], [100 , "C" ], [90 , "XC" ], [50 , "L" ], [40 , "XL" ], [10 , "X" ], [9 , "IX" ], [5 , "V" ], [4 , "IV" ], [1 , "I" ]]; const roman = []; for (const [value, symbol] of valueSymbols) { while (num >= value) { num -= value; roman.push (symbol); } if (num == 0 ) { break ; } } return roman.join ('' ); };
[sol1-Python3] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution : VALUE_SYMBOLS = [ (1000 , "M" ), (900 , "CM" ), (500 , "D" ), (400 , "CD" ), (100 , "C" ), (90 , "XC" ), (50 , "L" ), (40 , "XL" ), (10 , "X" ), (9 , "IX" ), (5 , "V" ), (4 , "IV" ), (1 , "I" ), ] def intToRoman (self, num: int ) -> str : roman = list () for value, symbol in Solution.VALUE_SYMBOLS: while num >= value: num -= value roman.append(symbol) if num == 0 : break return "" .join(roman)
[sol1-C] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 const int values[] = {1000 , 900 , 500 , 400 , 100 , 90 , 50 , 40 , 10 , 9 , 5 , 4 , 1 };const char * symbols[] = {"M" , "CM" , "D" , "CD" , "C" , "XC" , "L" , "XL" , "X" , "IX" , "V" , "IV" , "I" };char * intToRoman (int num) { char * roman = malloc (sizeof (char ) * 16 ); roman[0 ] = '\0' ; for (int i = 0 ; i < 13 ; i++) { while (num >= values[i]) { num -= values[i]; strcpy (roman + strlen (roman), symbols[i]); } if (num == 0 ) { break ; } } return roman; }
复杂度分析
方法二:硬编码数字 思路
回顾前言中列出的这 $13$ 个符号,可以发现:
千位数字只能由 $\texttt{M}$ 表示;
百位数字只能由 $\texttt{C}$,$\texttt{CD}$,$\texttt{D}$ 和 $\texttt{CM}$ 表示;
十位数字只能由 $\texttt{X}$,$\texttt{XL}$,$\texttt{L}$ 和 $\texttt{XC}$ 表示;
个位数字只能由 $\texttt{I}$,$\texttt{IV}$,$\texttt{V}$ 和 $\texttt{IX}$ 表示。
这恰好把这 $13$ 个符号分为四组,且组与组之间没有公共的符号。因此,整数 $\textit{num}$ 的十进制表示中的每一个数字都是可以单独处理的。
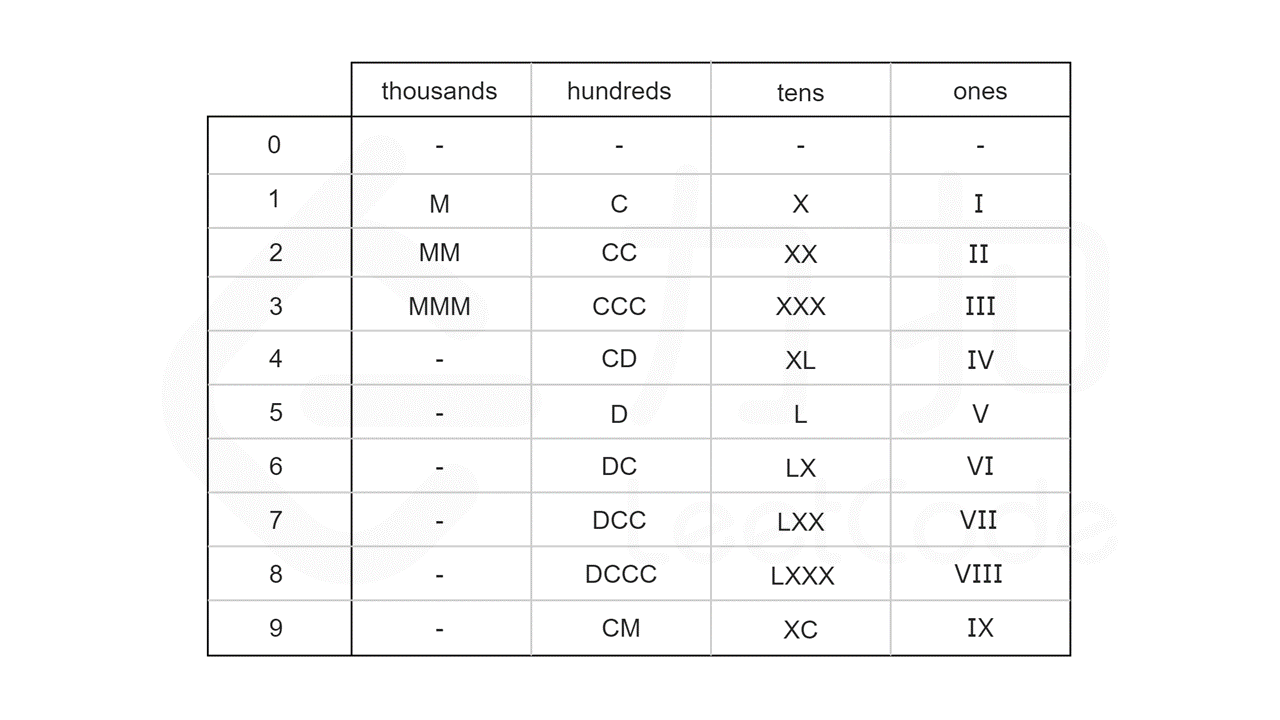
进一步地,我们可以计算出每个数字在每个位上的表示形式,整理成一张硬编码表。如下图所示,其中 $0$ 对应的是空字符串。
利用模运算和除法运算,我们可以得到 $\textit{num}$ 每个位上的数字:
1 2 3 4 thousands_digit = num / 1000 hundreds_digit = (num % 1000) / 100 tens_digit = (num % 100) / 10 ones_digit = num % 10
最后,根据 $\textit{num}$ 每个位上的数字,在硬编码表中查找对应的罗马字符,并将结果拼接在一起,即为 $\textit{num}$ 对应的罗马数字。
代码
[sol2-C++] 1 2 3 4 5 6 7 8 9 10 11 const string thousands[] = {"" , "M" , "MM" , "MMM" };const string hundreds[] = {"" , "C" , "CC" , "CCC" , "CD" , "D" , "DC" , "DCC" , "DCCC" , "CM" };const string tens[] = {"" , "X" , "XX" , "XXX" , "XL" , "L" , "LX" , "LXX" , "LXXX" , "XC" };const string ones[] = {"" , "I" , "II" , "III" , "IV" , "V" , "VI" , "VII" , "VIII" , "IX" };class Solution {public : string intToRoman (int num) { return thousands[num / 1000 ] + hundreds[num % 1000 / 100 ] + tens[num % 100 / 10 ] + ones[num % 10 ]; } };
[sol2-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution { String[] thousands = {"" , "M" , "MM" , "MMM" }; String[] hundreds = {"" , "C" , "CC" , "CCC" , "CD" , "D" , "DC" , "DCC" , "DCCC" , "CM" }; String[] tens = {"" , "X" , "XX" , "XXX" , "XL" , "L" , "LX" , "LXX" , "LXXX" , "XC" }; String[] ones = {"" , "I" , "II" , "III" , "IV" , "V" , "VI" , "VII" , "VIII" , "IX" }; public String intToRoman (int num) { StringBuffer roman = new StringBuffer (); roman.append(thousands[num / 1000 ]); roman.append(hundreds[num % 1000 / 100 ]); roman.append(tens[num % 100 / 10 ]); roman.append(ones[num % 10 ]); return roman.toString(); } }
[sol2-C#] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 public class Solution { readonly string [] thousands = {"" , "M" , "MM" , "MMM" }; readonly string [] hundreds = {"" , "C" , "CC" , "CCC" , "CD" , "D" , "DC" , "DCC" , "DCCC" , "CM" }; readonly string [] tens = {"" , "X" , "XX" , "XXX" , "XL" , "L" , "LX" , "LXX" , "LXXX" , "XC" }; readonly string [] ones = {"" , "I" , "II" , "III" , "IV" , "V" , "VI" , "VII" , "VIII" , "IX" }; public string IntToRoman (int num StringBuilder roman = new StringBuilder(); roman.Append(thousands[num / 1000 ]); roman.Append(hundreds[num % 1000 / 100 ]); roman.Append(tens[num % 100 / 10 ]); roman.Append(ones[num % 10 ]); return roman.ToString(); } }
[sol2-Golang] 1 2 3 4 5 6 7 8 9 10 var ( thousands = []string {"" , "M" , "MM" , "MMM" } hundreds = []string {"" , "C" , "CC" , "CCC" , "CD" , "D" , "DC" , "DCC" , "DCCC" , "CM" } tens = []string {"" , "X" , "XX" , "XXX" , "XL" , "L" , "LX" , "LXX" , "LXXX" , "XC" } ones = []string {"" , "I" , "II" , "III" , "IV" , "V" , "VI" , "VII" , "VIII" , "IX" } ) func intToRoman (num int ) string { return thousands[num/1000 ] + hundreds[num%1000 /100 ] + tens[num%100 /10 ] + ones[num%10 ] }
[sol2-JavaScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 var intToRoman = function (num ) { const thousands = ["" , "M" , "MM" , "MMM" ]; const hundreds = ["" , "C" , "CC" , "CCC" , "CD" , "D" , "DC" , "DCC" , "DCCC" , "CM" ]; const tens = ["" , "X" , "XX" , "XXX" , "XL" , "L" , "LX" , "LXX" , "LXXX" , "XC" ]; const ones = ["" , "I" , "II" , "III" , "IV" , "V" , "VI" , "VII" , "VIII" , "IX" ]; const roman = []; roman.push (thousands[Math .floor (num / 1000 )]); roman.push (hundreds[Math .floor (num % 1000 / 100 )]); roman.push (tens[Math .floor (num % 100 / 10 )]); roman.push (ones[num % 10 ]); return roman.join ('' ); };
[sol2-Python3] 1 2 3 4 5 6 7 8 9 10 11 12 class Solution : THOUSANDS = ["" , "M" , "MM" , "MMM" ] HUNDREDS = ["" , "C" , "CC" , "CCC" , "CD" , "D" , "DC" , "DCC" , "DCCC" , "CM" ] TENS = ["" , "X" , "XX" , "XXX" , "XL" , "L" , "LX" , "LXX" , "LXXX" , "XC" ] ONES = ["" , "I" , "II" , "III" , "IV" , "V" , "VI" , "VII" , "VIII" , "IX" ] def intToRoman (self, num: int ) -> str : return Solution.THOUSANDS[num // 1000 ] + \ Solution.HUNDREDS[num % 1000 // 100 ] + \ Solution.TENS[num % 100 // 10 ] + \ Solution.ONES[num % 10 ]
[sol2-C] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 const char * thousands[] = {"" , "M" , "MM" , "MMM" };const char * hundreds[] = {"" , "C" , "CC" , "CCC" , "CD" , "D" , "DC" , "DCC" , "DCCC" , "CM" };const char * tens[] = {"" , "X" , "XX" , "XXX" , "XL" , "L" , "LX" , "LXX" , "LXXX" , "XC" };const char * ones[] = {"" , "I" , "II" , "III" , "IV" , "V" , "VI" , "VII" , "VIII" , "IX" };char * intToRoman (int num) { char * roman = malloc (sizeof (char ) * 16 ); roman[0 ] = '\0' ; strcpy (roman + strlen (roman), thousands[num / 1000 ]); strcpy (roman + strlen (roman), hundreds[num % 1000 / 100 ]); strcpy (roman + strlen (roman), tens[num % 100 / 10 ]); strcpy (roman + strlen (roman), ones[num % 10 ]); return roman; }
复杂度分析