0017-电话号码的字母组合

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 10:40:35 2023-09-13 10:40:35 Updated    

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

![](https://assets.leetcode-cn.com/aliyun-lc-upload/uploads/2021/11/09/200px-
telephone-keypad2svg.png)

示例 1：

**输入：** digits = "23"
**输出：** ["ad","ae","af","bd","be","bf","cd","ce","cf"]

示例 2：

**输入：** digits = ""
**输出：** []

示例 3：

**输入：** digits = "2"
**输出：** ["a","b","c"]

提示：

  • 0 <= digits.length <= 4
  • digits[i] 是范围 ['2', '9'] 的一个数字。

📺 视频题解

17. 电话号码的字母组合.mp4

📖 文字题解

方法一：回溯

首先使用哈希表存储每个数字对应的所有可能的字母，然后进行回溯操作。

回溯过程中维护一个字符串，表示已有的字母排列（如果未遍历完电话号码的所有数字，则已有的字母排列是不完整的）。该字符串初始为空。每次取电话号码的一位数字，从哈希表中获得该数字对应的所有可能的字母，并将其中的一个字母插入到已有的字母排列后面，然后继续处理电话号码的后一位数字，直到处理完电话号码中的所有数字，即得到一个完整的字母排列。然后进行回退操作，遍历其余的字母排列。

回溯算法用于寻找所有的可行解，如果发现一个解不可行，则会舍弃不可行的解。在这道题中，由于每个数字对应的每个字母都可能进入字母组合，因此不存在不可行的解，直接穷举所有的解即可。

<fig1,fig2,fig3,fig4,fig5,fig6,fig7,fig8,fig9,fig10,fig11,fig12,fig13,fig14>

[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
    public List<String> letterCombinations(String digits) {
        List<String> combinations = new ArrayList<String>();
        if (digits.length() == 0) {
            return combinations;
        }
        Map<Character, String> phoneMap = new HashMap<Character, String>() {{
            put('2', "abc");
            put('3', "def");
            put('4', "ghi");
            put('5', "jkl");
            put('6', "mno");
            put('7', "pqrs");
            put('8', "tuv");
            put('9', "wxyz");
        }};
        backtrack(combinations, phoneMap, digits, 0, new StringBuffer());
        return combinations;
    }

    public void backtrack(List<String> combinations, Map<Character, String> phoneMap, String digits, int index, StringBuffer combination) {
        if (index == digits.length()) {
            combinations.add(combination.toString());
        } else {
            char digit = digits.charAt(index);
            String letters = phoneMap.get(digit);
            int lettersCount = letters.length();
            for (int i = 0; i < lettersCount; i++) {
                combination.append(letters.charAt(i));
                backtrack(combinations, phoneMap, digits, index + 1, combination);
                combination.deleteCharAt(index);
            }
        }
    }
}
[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
public:
    vector<string> letterCombinations(string digits) {
        vector<string> combinations;
        if (digits.empty()) {
            return combinations;
        }
        unordered_map<char, string> phoneMap{
            {'2', "abc"},
            {'3', "def"},
            {'4', "ghi"},
            {'5', "jkl"},
            {'6', "mno"},
            {'7', "pqrs"},
            {'8', "tuv"},
            {'9', "wxyz"}
        };
        string combination;
        backtrack(combinations, phoneMap, digits, 0, combination);
        return combinations;
    }

    void backtrack(vector<string>& combinations, const unordered_map<char, string>& phoneMap, const string& digits, int index, string& combination) {
        if (index == digits.length()) {
            combinations.push_back(combination);
        } else {
            char digit = digits[index];
            const string& letters = phoneMap.at(digit);
            for (const char& letter: letters) {
                combination.push_back(letter);
                backtrack(combinations, phoneMap, digits, index + 1, combination);
                combination.pop_back();
            }
        }
    }
};
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
var phoneMap map[string]string = map[string]string{
    "2": "abc",
    "3": "def",
    "4": "ghi",
    "5": "jkl",
    "6": "mno",
    "7": "pqrs",
    "8": "tuv",
    "9": "wxyz",
}

var combinations []string

func letterCombinations(digits string) []string {
    if len(digits) == 0 {
        return []string{}
    }
    combinations = []string{}
    backtrack(digits, 0, "")
    return combinations
}

func backtrack(digits string, index int, combination string) {
    if index == len(digits) {
        combinations = append(combinations, combination)
    } else {
        digit := string(digits[index])
        letters := phoneMap[digit]
        lettersCount := len(letters)
        for i := 0; i < lettersCount; i++ {
            backtrack(digits, index + 1, combination + string(letters[i]))
        }
    }
}
[sol1-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
char phoneMap[11][5] = {"\0", "\0", "abc\0", "def\0", "ghi\0", "jkl\0", "mno\0", "pqrs\0", "tuv\0", "wxyz\0"};

char* digits_tmp;
int digits_size;

char** combinations;
int combinations_size;

char* combination;
int combination_size;

void backtrack(int index) {
    if (index == digits_size) {
        char* tmp = malloc(sizeof(char) * (combination_size + 1));
        memcpy(tmp, combination, sizeof(char) * (combination_size + 1));
        combinations[combinations_size++] = tmp;
    } else {
        char digit = digits_tmp[index];
        char* letters = phoneMap[digit - '0'];
        int len = strlen(letters);
        for (int i = 0; i < len; i++) {
            combination[combination_size++] = letters[i];
            combination[combination_size] = 0;
            backtrack(index + 1);
            combination[--combination_size] = 0;
        }
    }
}

char** letterCombinations(char* digits, int* returnSize) {
    combinations_size = combination_size = 0;
    digits_tmp = digits;
    digits_size = strlen(digits);
    if (digits_size == 0) {
        *returnSize = 0;
        return combinations;
    }
    int num = 1;
    for (int i = 0; i < digits_size; i++) num *= 4;
    combinations = malloc(sizeof(char*) * num);
    combination = malloc(sizeof(char*) * digits_size);
    backtrack(0);
    *returnSize = combinations_size;
    return combinations;
}
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution:
    def letterCombinations(self, digits: str) -> List[str]:
        if not digits:
            return list()
        
        phoneMap = {
            "2": "abc",
            "3": "def",
            "4": "ghi",
            "5": "jkl",
            "6": "mno",
            "7": "pqrs",
            "8": "tuv",
            "9": "wxyz",
        }

        def backtrack(index: int):
            if index == len(digits):
                combinations.append("".join(combination))
            else:
                digit = digits[index]
                for letter in phoneMap[digit]:
                    combination.append(letter)
                    backtrack(index + 1)
                    combination.pop()

        combination = list()
        combinations = list()
        backtrack(0)
        return combinations
[sol1-Python3_oneliner]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution:
    def letterCombinations(self, digits: str) -> List[str]:
        if not digits:
            return list()
        
        phoneMap = {
            "2": "abc",
            "3": "def",
            "4": "ghi",
            "5": "jkl",
            "6": "mno",
            "7": "pqrs",
            "8": "tuv",
            "9": "wxyz",
        }

        groups = (phoneMap[digit] for digit in digits)
        return ["".join(combination) for combination in itertools.product(*groups)]

复杂度分析

  • 时间复杂度：$O(3^m \times 4^n)$，其中 $m$ 是输入中对应 $3$ 个字母的数字个数（包括数字 $2$、$3$、$4$、$5$、$6$、$8$），$n$ 是输入中对应 $4$ 个字母的数字个数（包括数字 $7$、$9$），$m+n$ 是输入数字的总个数。当输入包含 $m$ 个对应 $3$ 个字母的数字和 $n$ 个对应 $4$ 个字母的数字时，不同的字母组合一共有 $3^m \times 4^n$ 种，需要遍历每一种字母组合。

  • 空间复杂度：$O(m+n)$，其中 $m$ 是输入中对应 $3$ 个字母的数字个数，$n$ 是输入中对应 $4$ 个字母的数字个数，$m+n$ 是输入数字的总个数。除了返回值以外，空间复杂度主要取决于哈希表以及回溯过程中的递归调用层数，哈希表的大小与输入无关，可以看成常数，递归调用层数最大为 $m+n$。

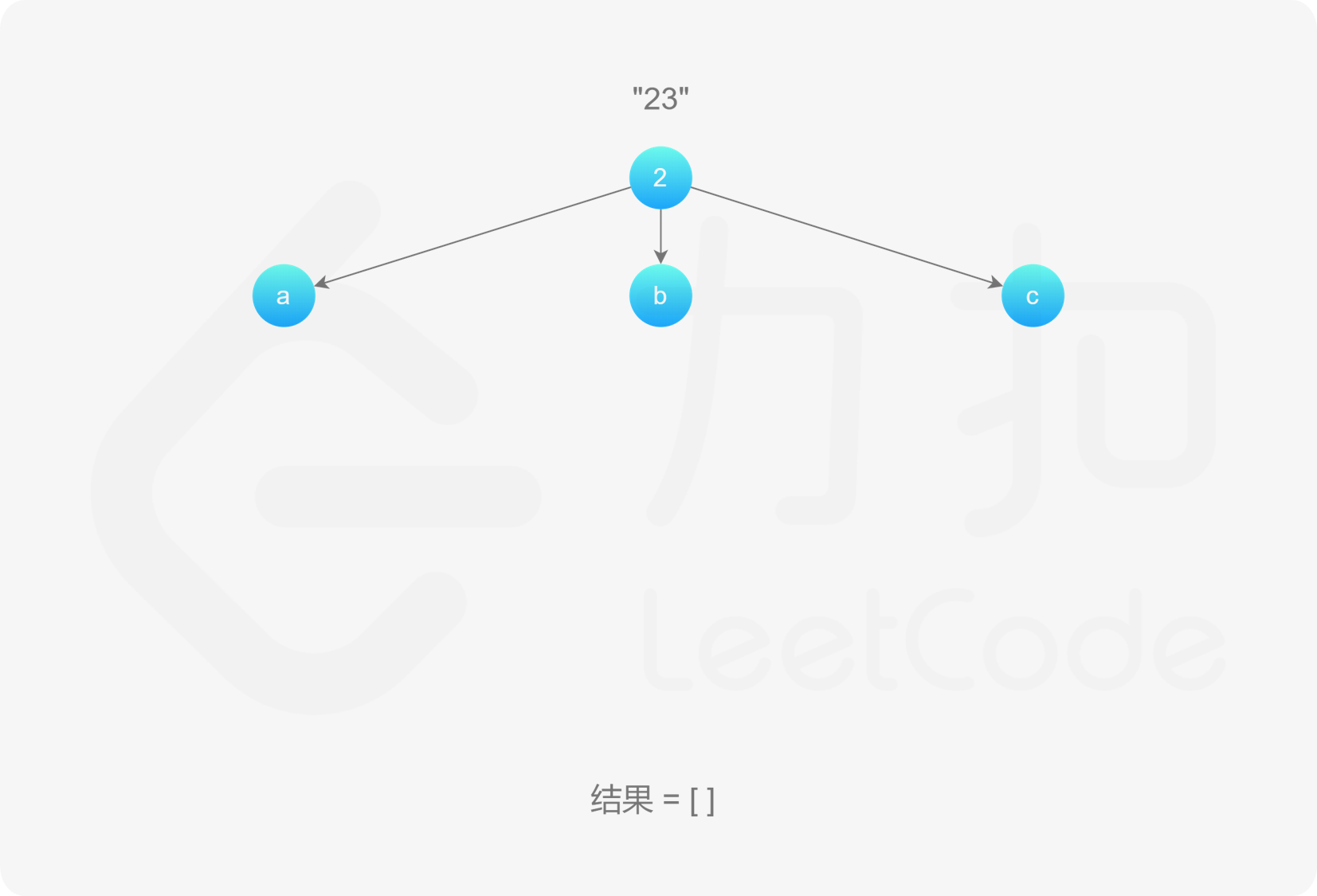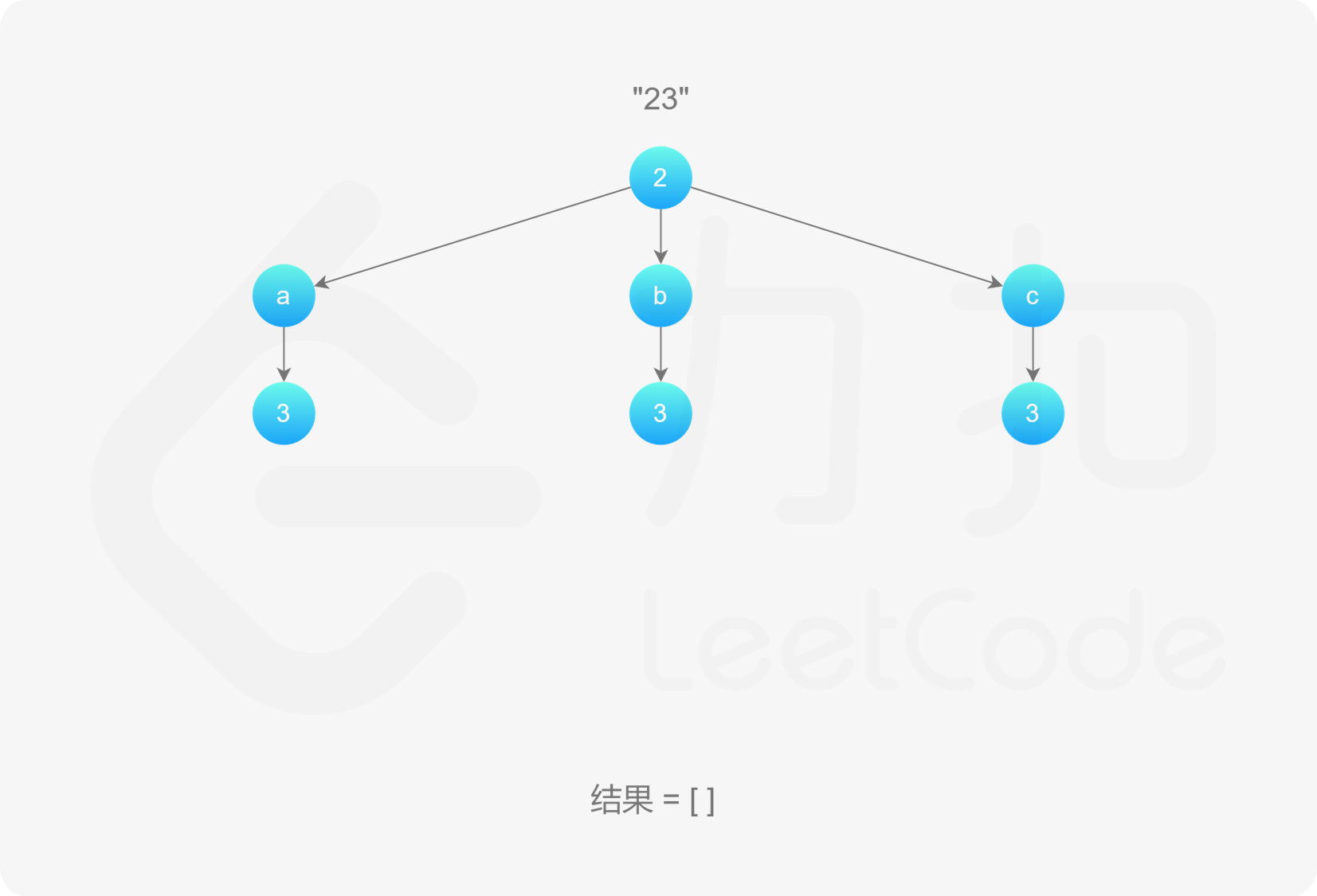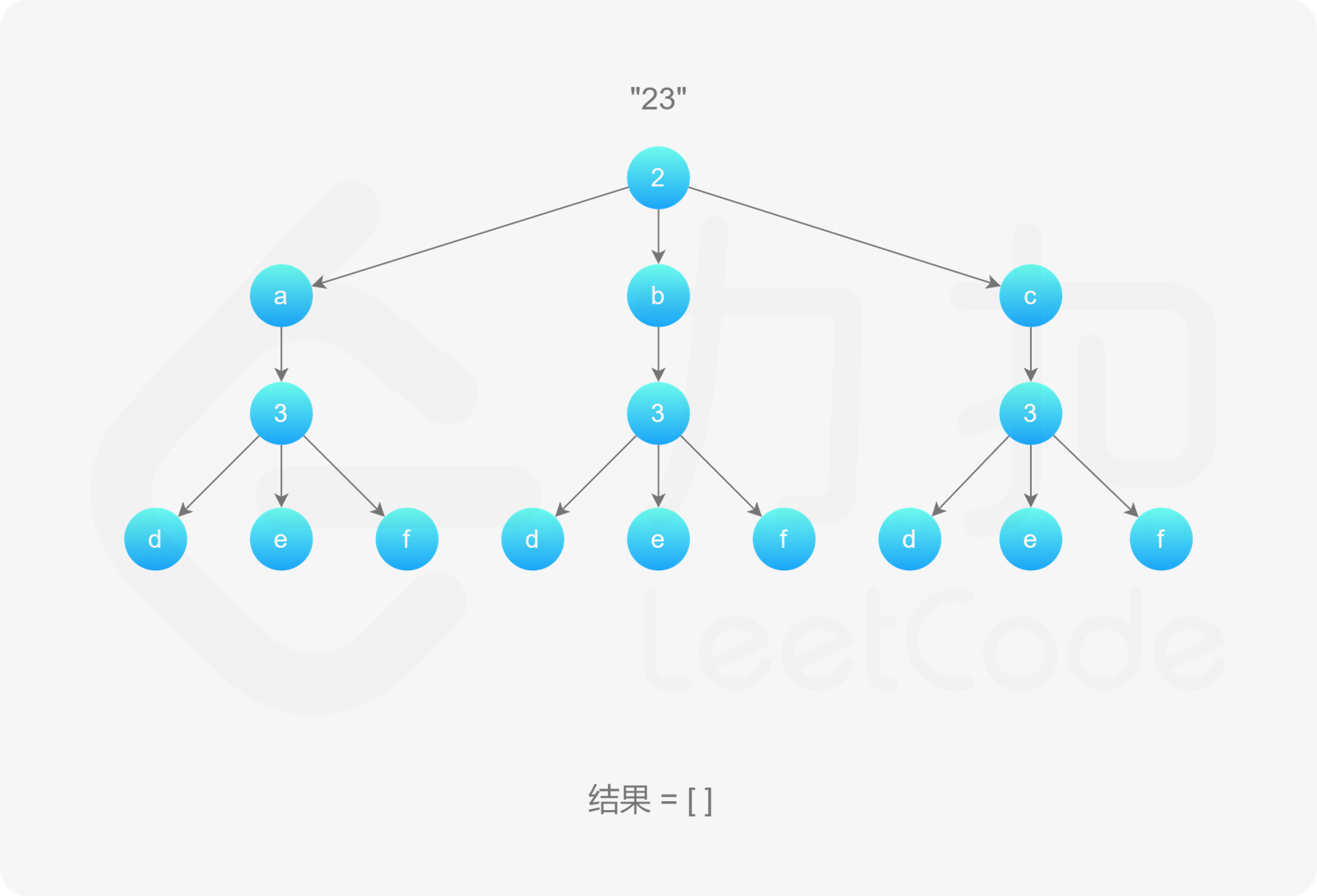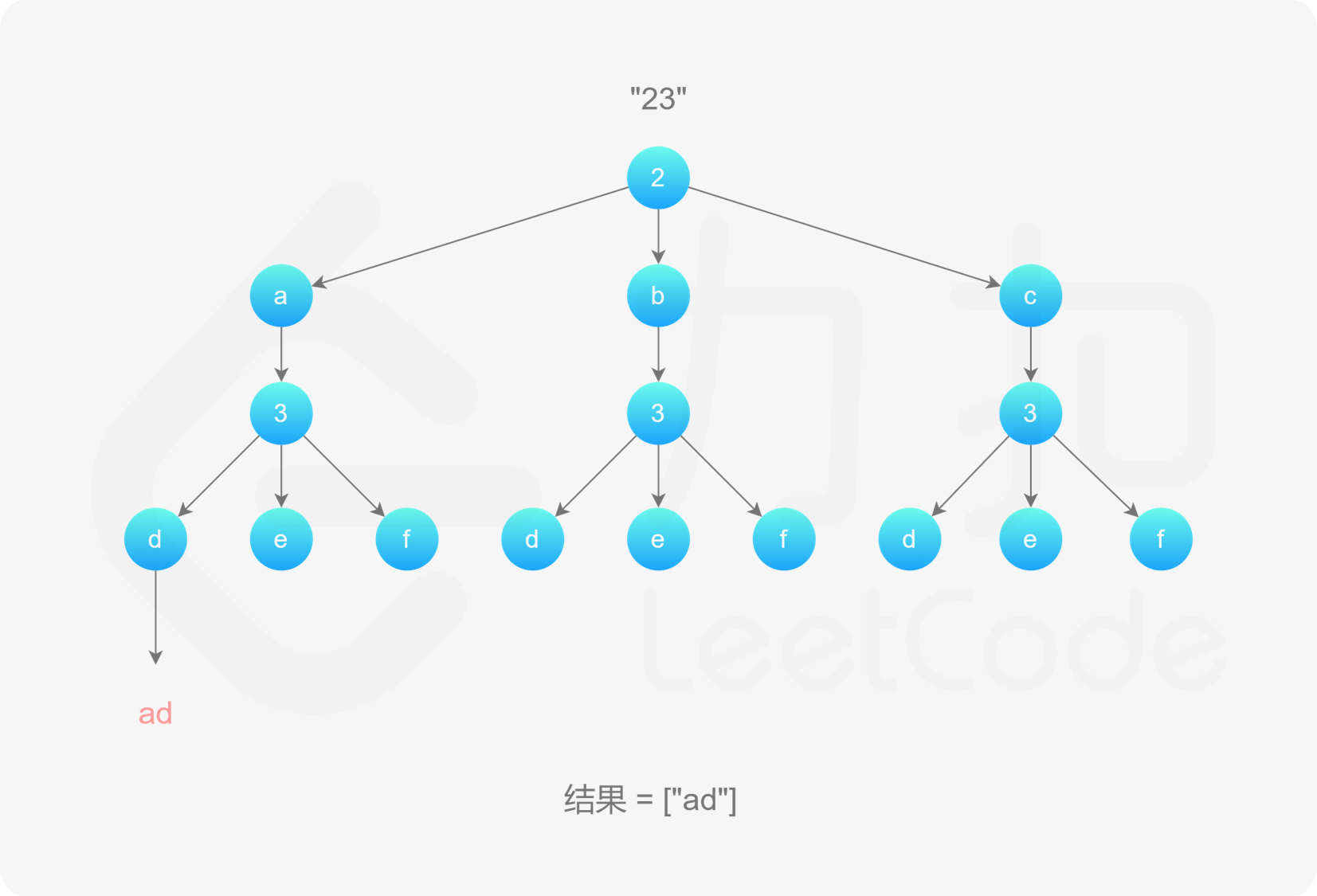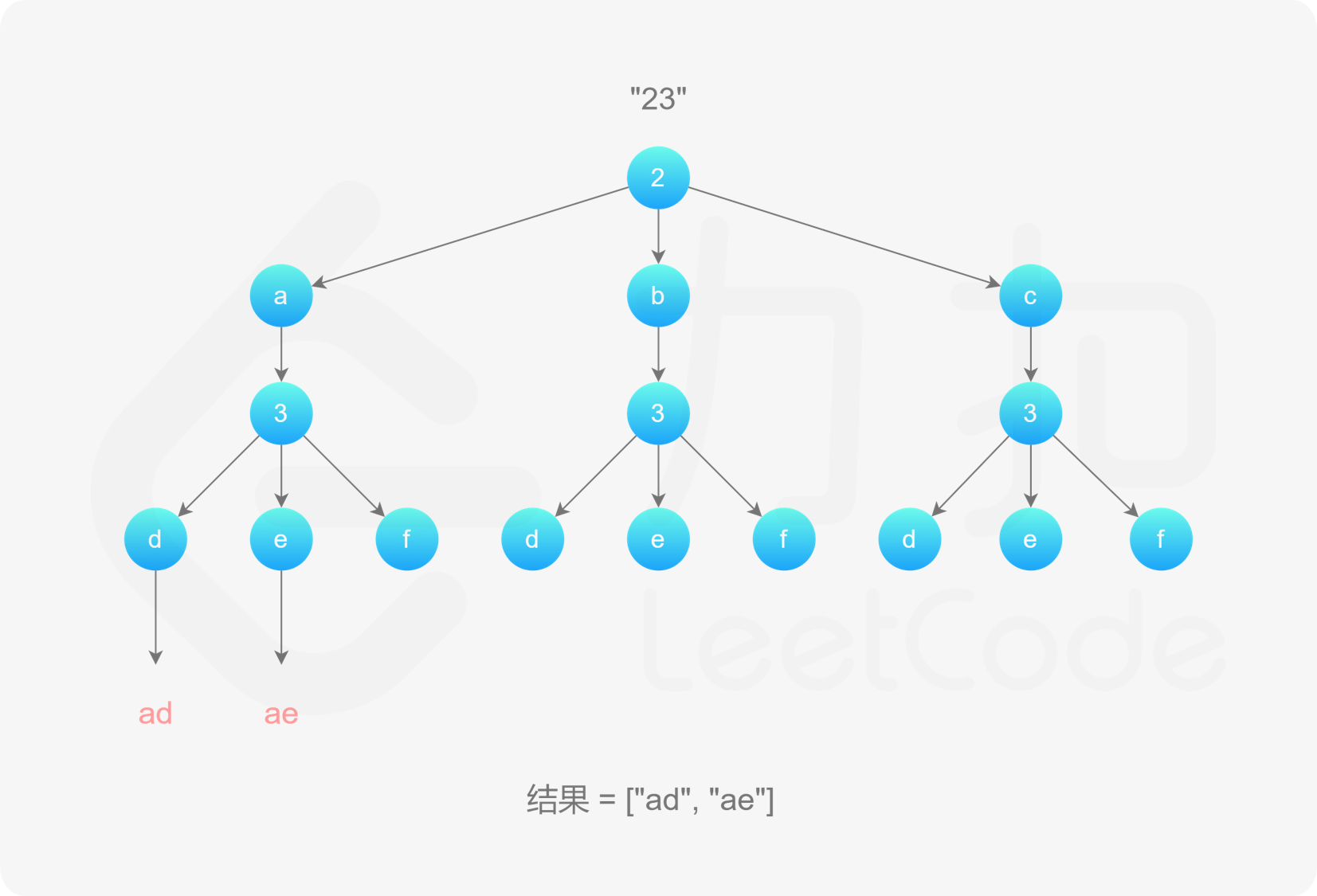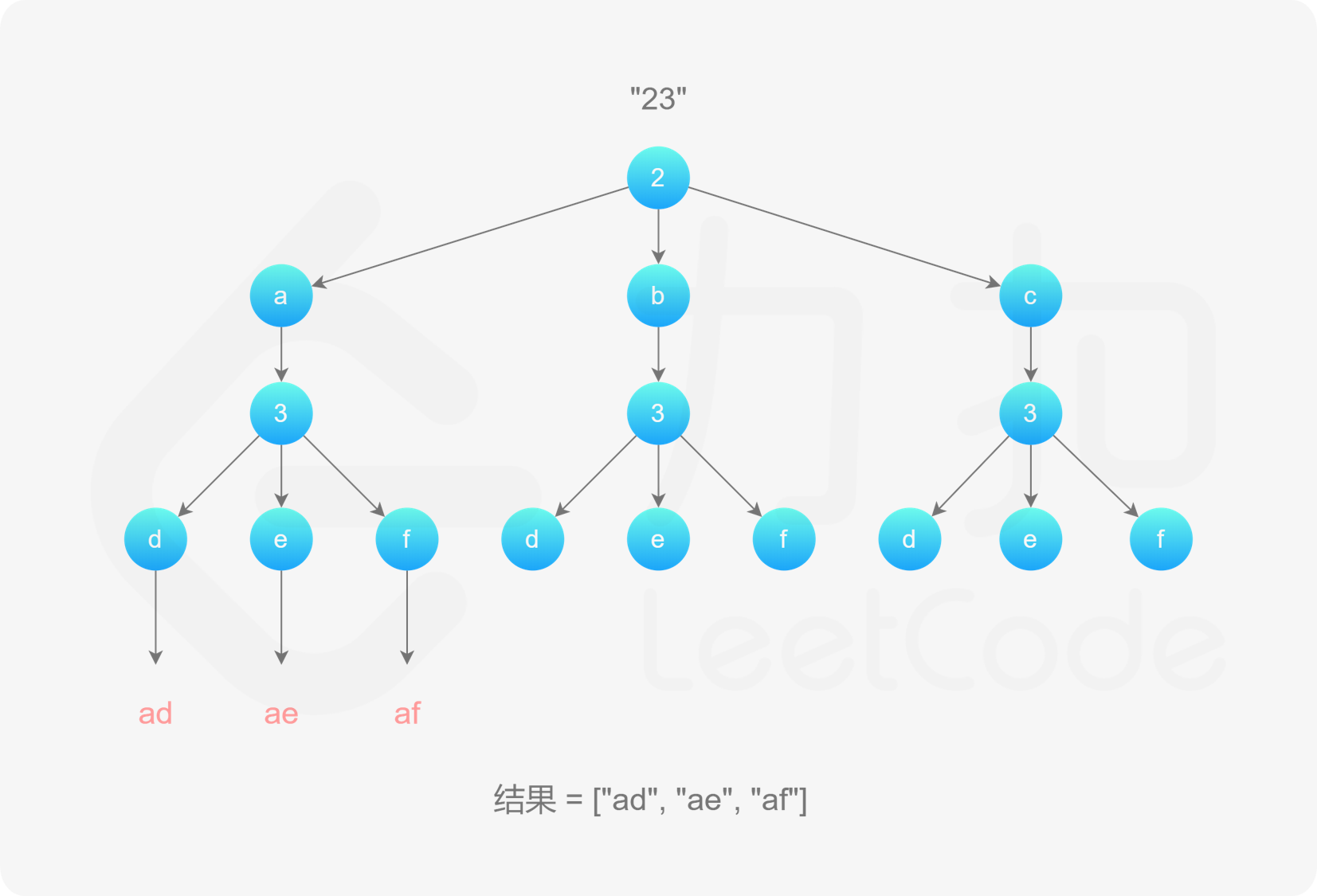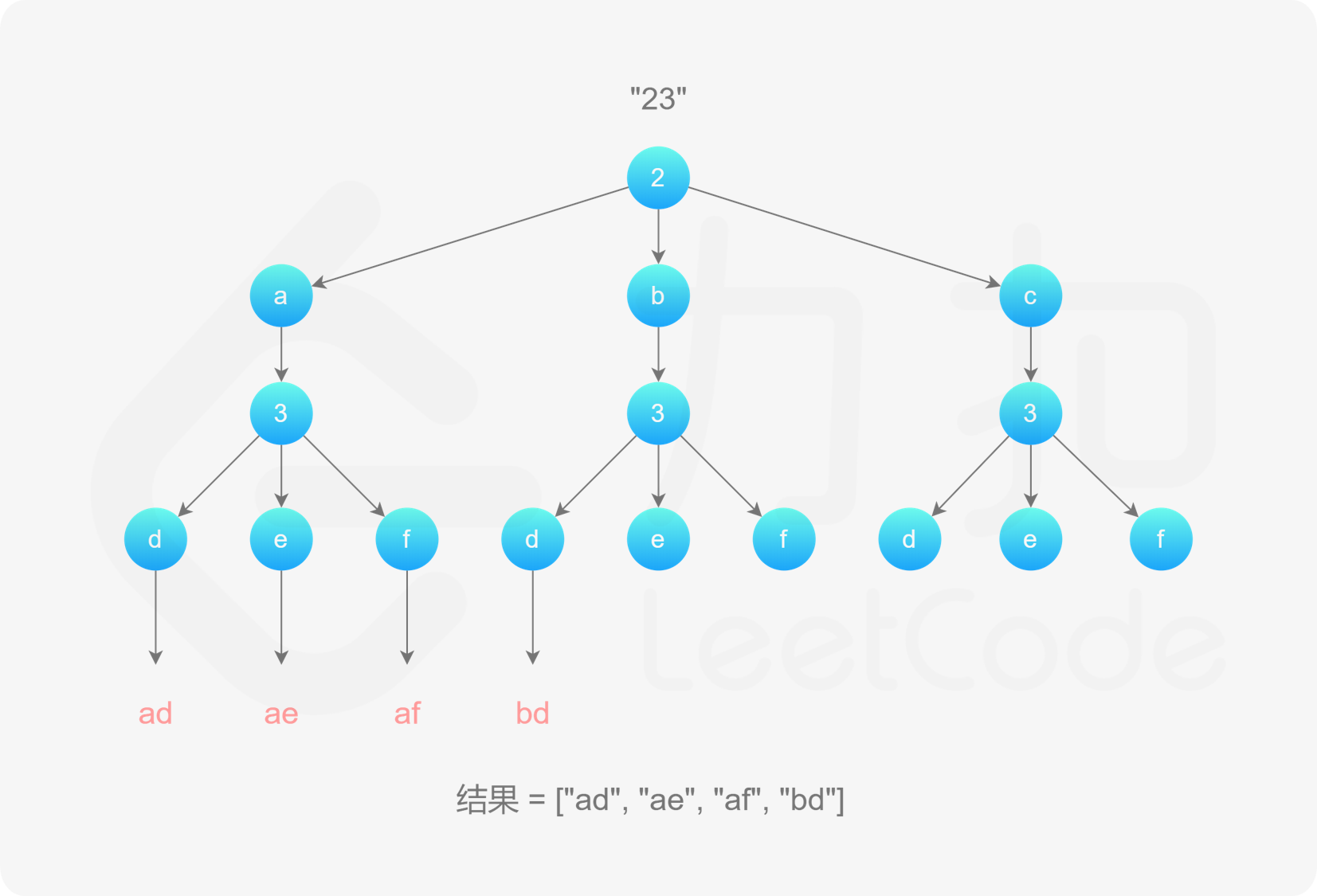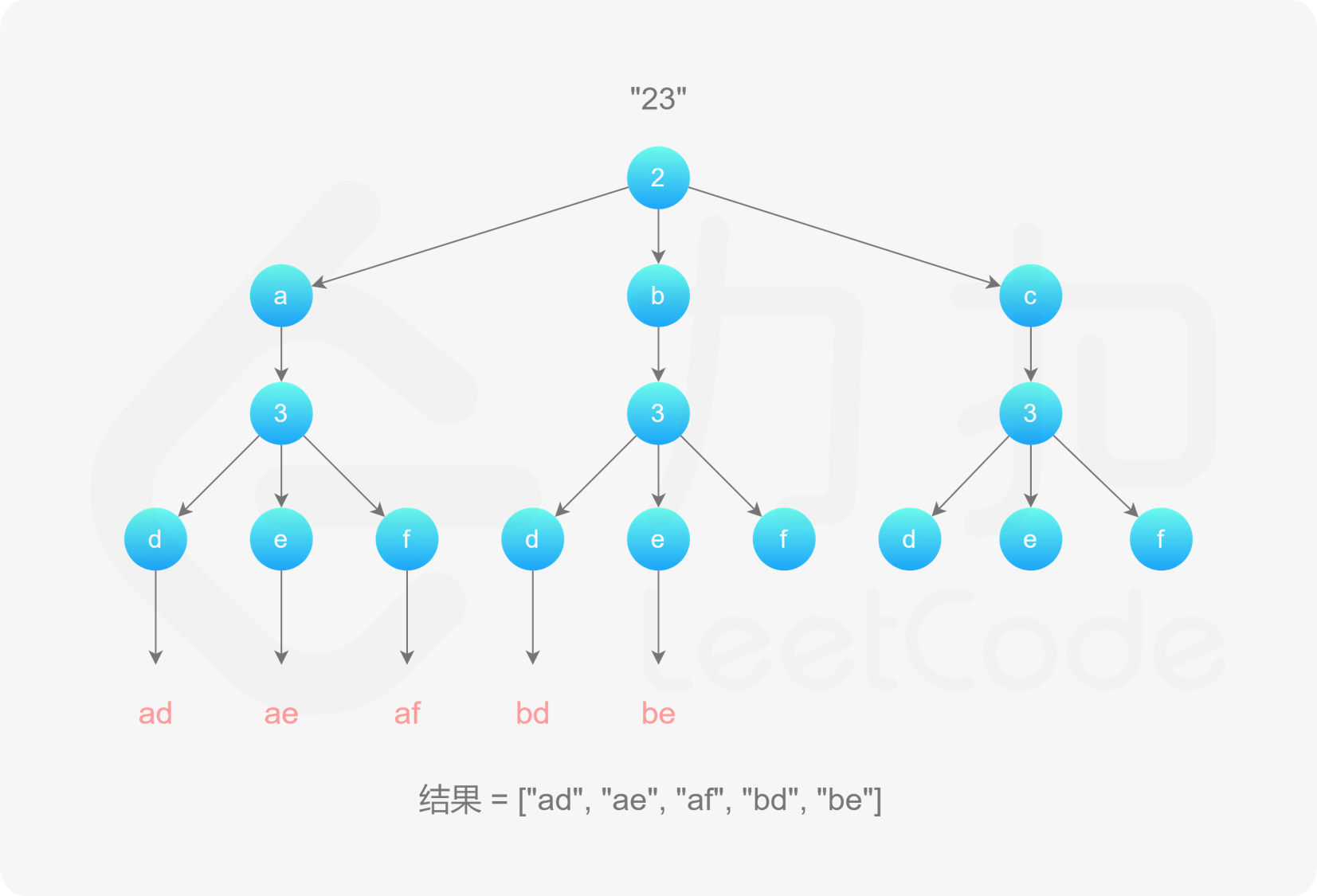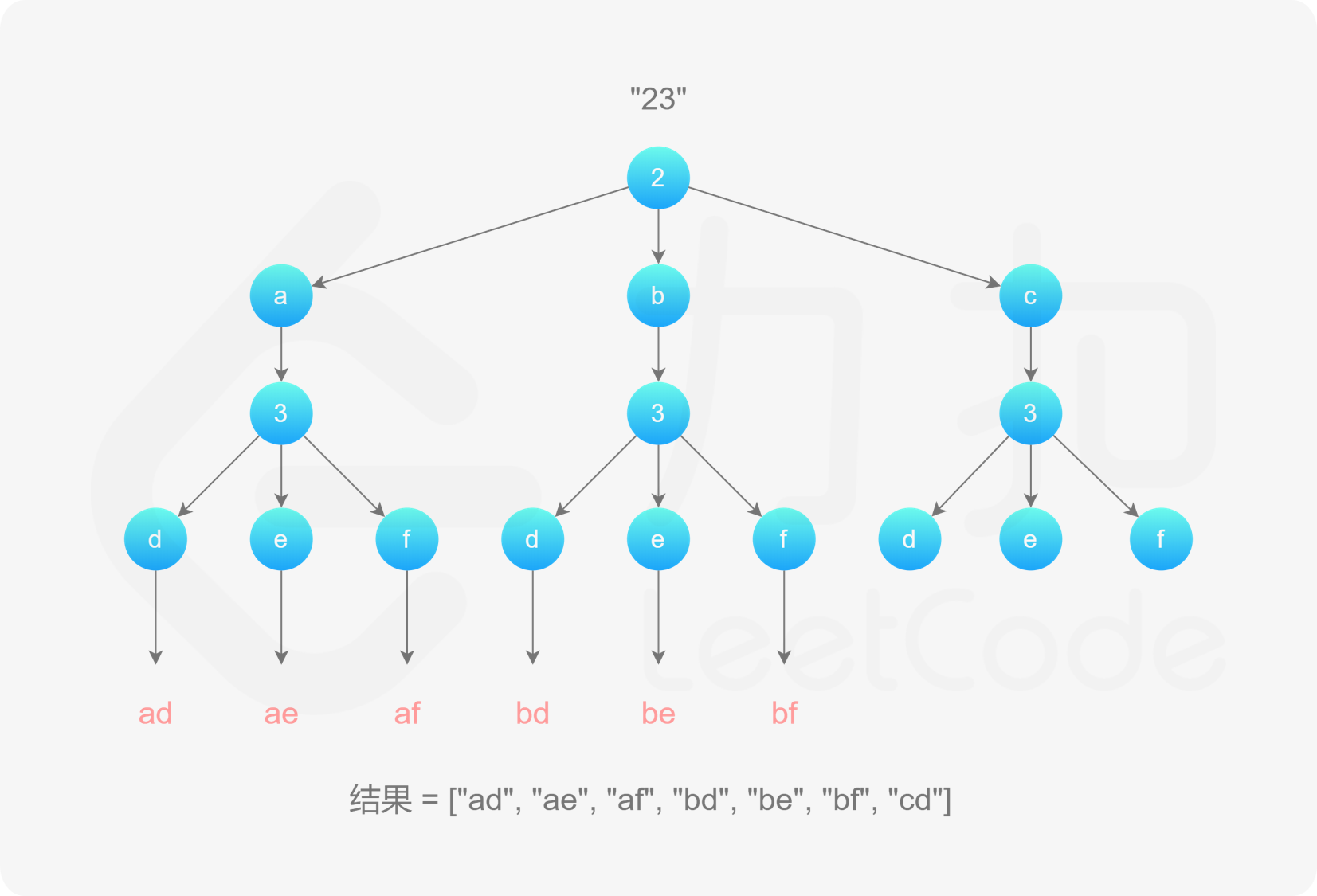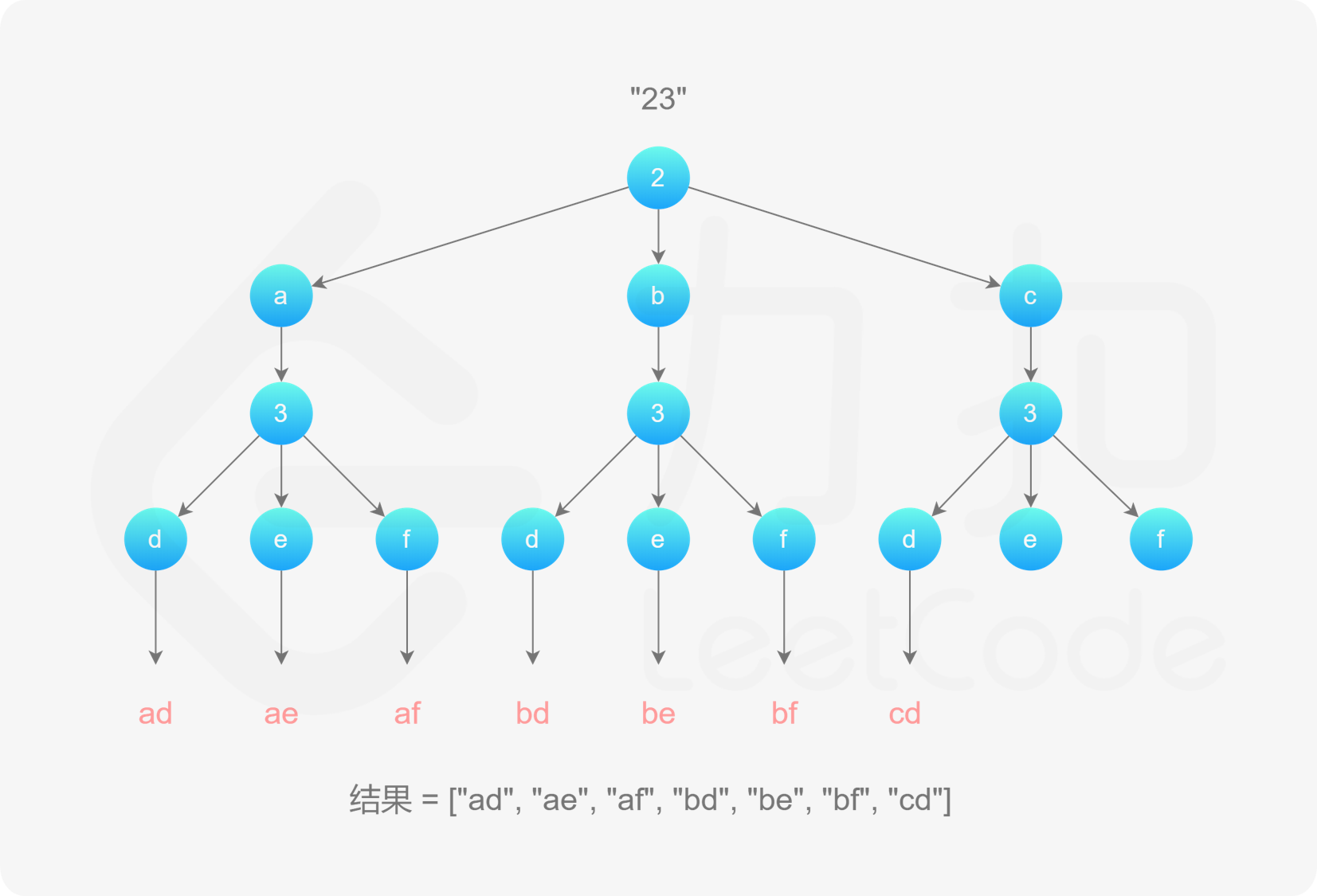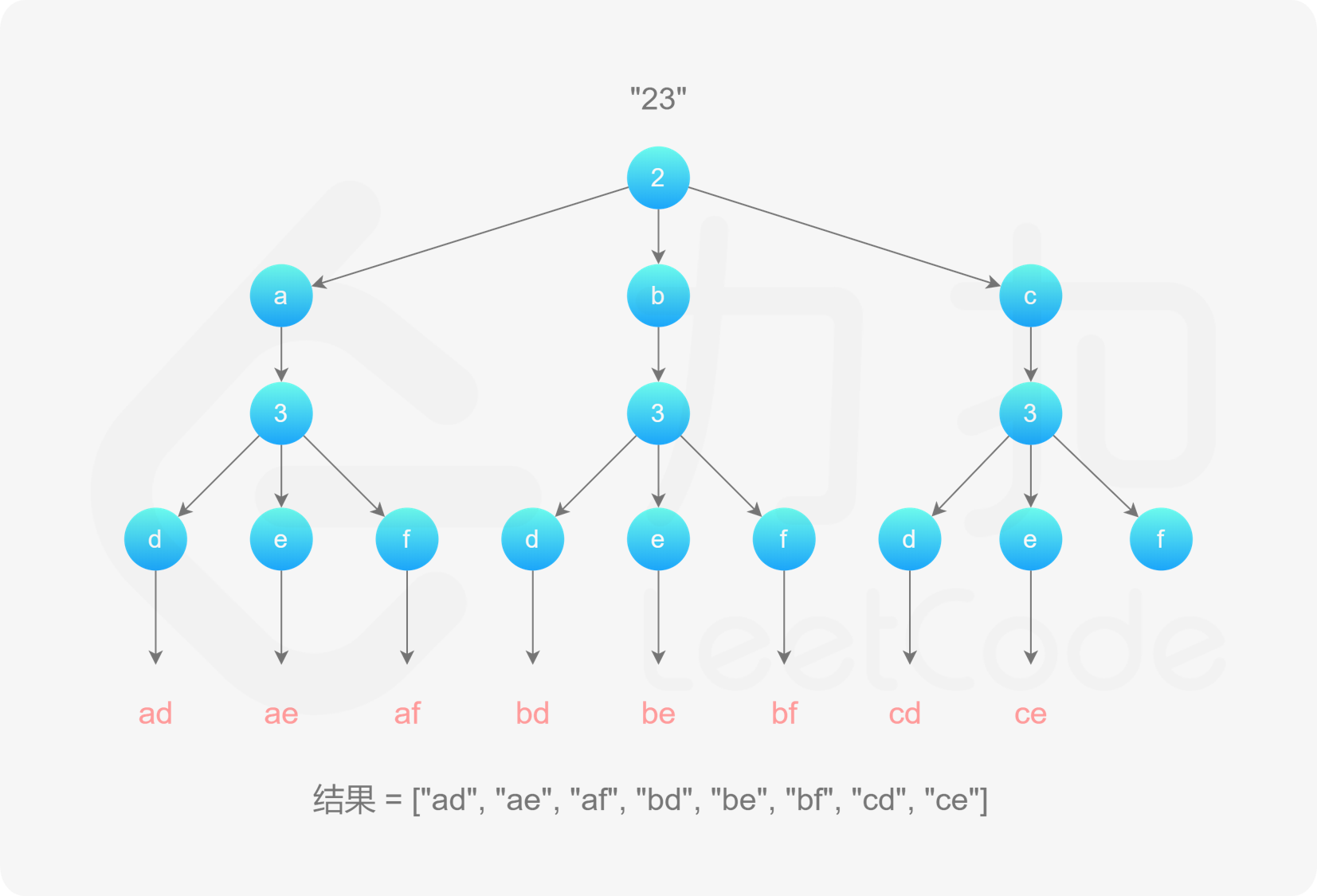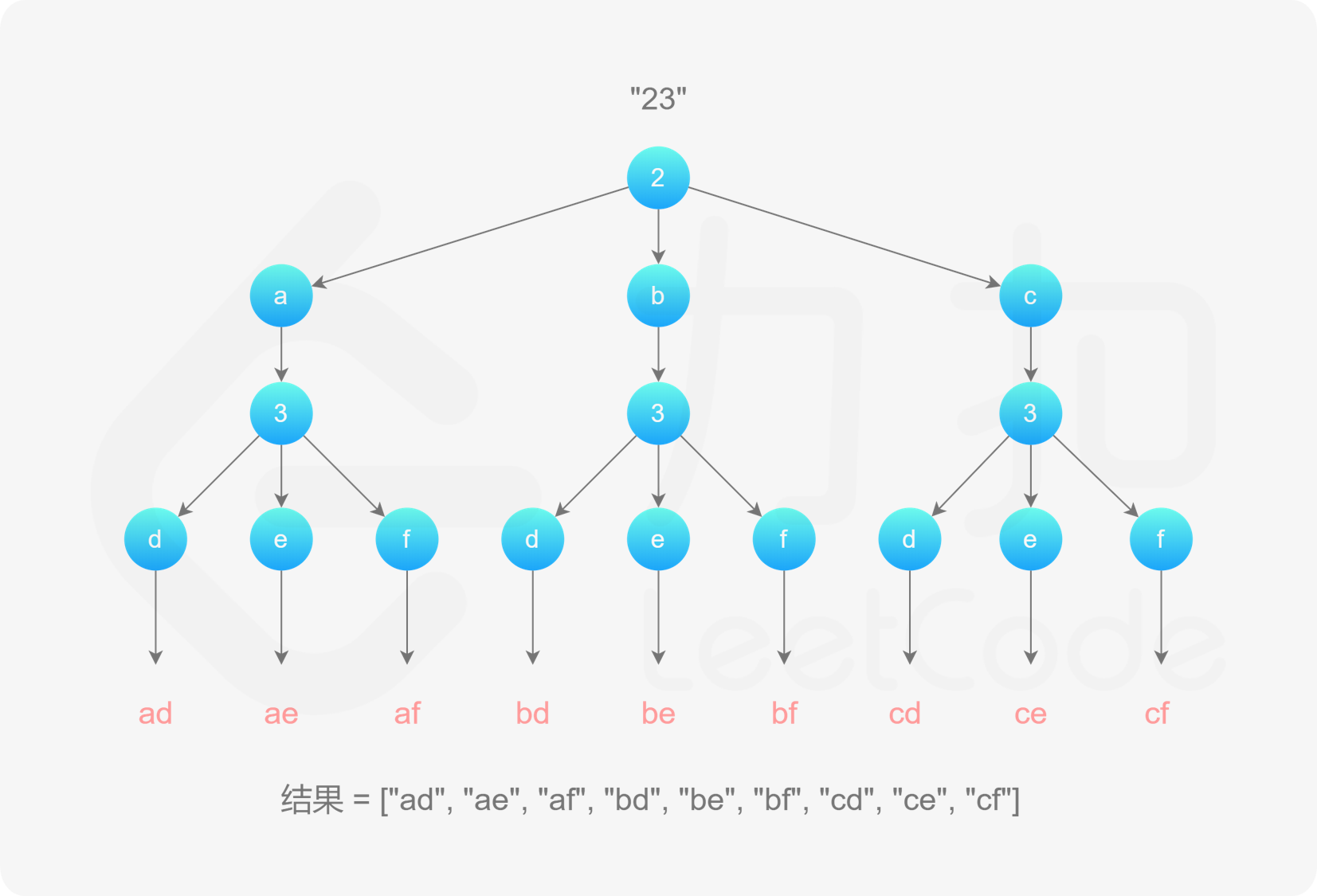 Comments
On this page
0017-电话号码的字母组合
  1. 📺 视频题解
  2. 📖 文字题解