0021-合并两个有序链表

将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例 1：

**输入：** l1 = [1,2,4], l2 = [1,3,4]
**输出：** [1,1,2,3,4,4]

示例 2：

**输入：** l1 = [], l2 = []
**输出：** []

示例 3：

**输入：** l1 = [], l2 = [0]
**输出：** [0]

提示：

两个链表的节点数目范围是 [0, 50]
-100 <= Node.val <= 100
l1 和 l2 均按 非递减顺序 排列

1. 前言

递归解法总是给人一种 “只可意会不可言传” 的感觉，代码一看就懂，自己动手一写就呆住了，很难受。究其原因，一是我们练习不够，二是理解不够。

2. 什么是递归？

递归的例子在平时生活中很容易见到，比如：

开个玩笑😁

什么是递归呢？函数在运行时调用自己，这个函数就叫递归函数，调用的过程叫做递归。
比如定义函数 $f(x)=x+f(x-1)$：

[]def f(x):
    return x + f(x-1)

如果代入 $f(2)$：

返回 $2+f(1)$；
调用 $f(1)$；
返回 $1+f(0)$；
调用 $f(0)$；
返回 $0+f(-1)$
……

这时程序会无休止地运行下去，直到崩溃。
如果我们加一个判断语句 x > 0：

[]def f(x):
    if x > 0:
        return x + f(x-1)
    else:  # f(0) = 0
        return 0

这次计算 $f(2)=2+f(1)=2+1+f(0)=2+1+0=3$。我们从中总结两个规律：

递归函数必须要有终止条件，否则会出错；
递归函数先不断调用自身，直到遇到终止条件后进行回溯，最终返回答案。

3. 递归解法

根据以上规律考虑本题目：

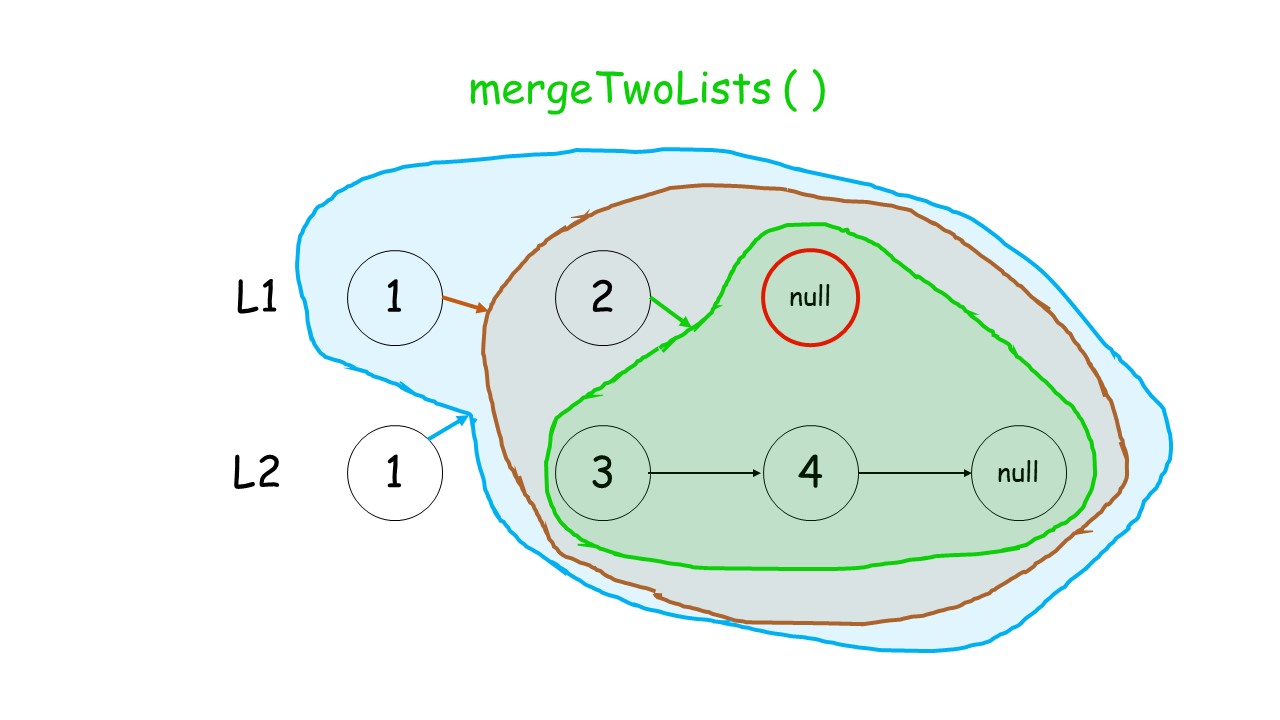
终止条件：当两个链表都为空时，表示我们对链表已合并完成。
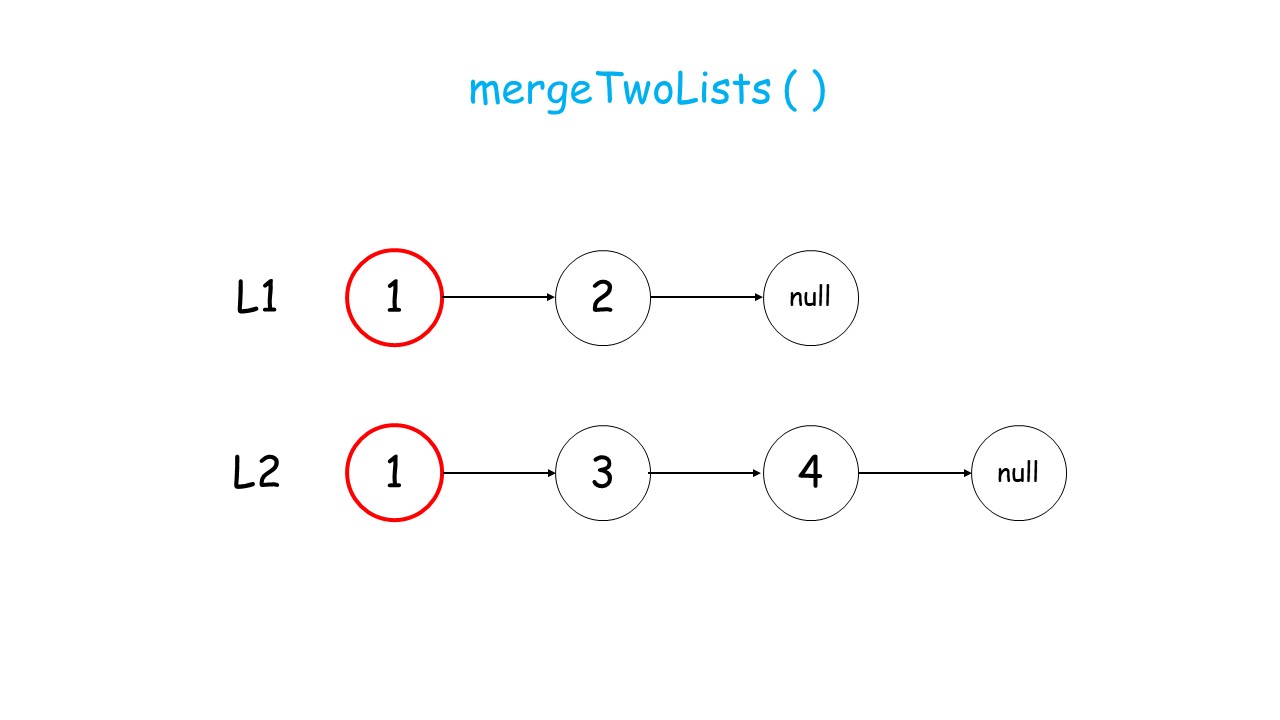
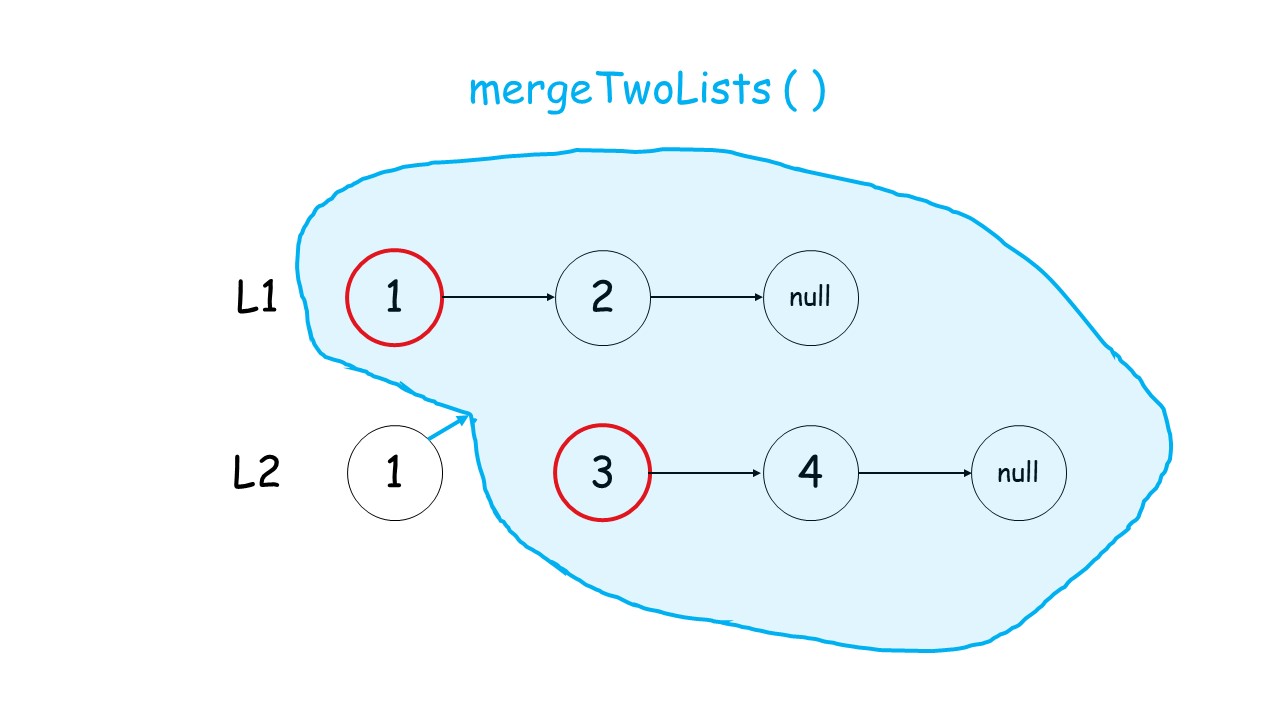
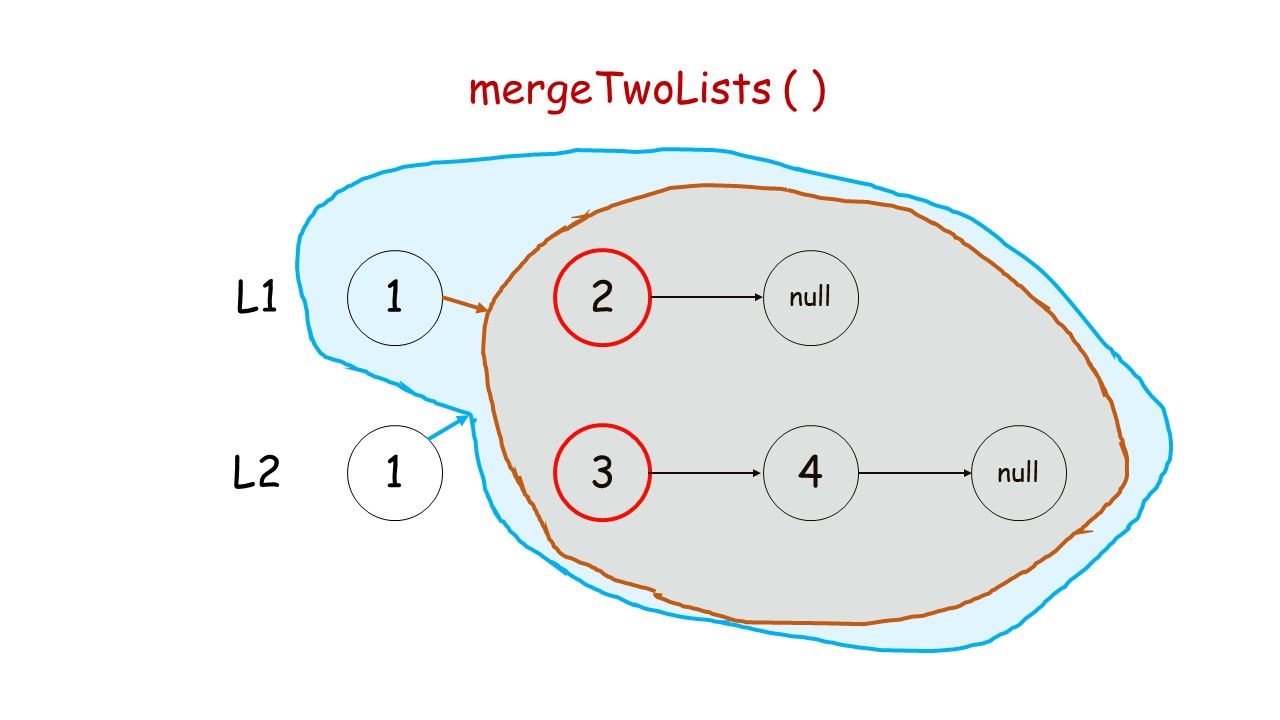
如何递归：我们判断 l1 和 l2 头结点哪个更小，然后较小结点的 next 指针指向其余结点的合并结果。（调用递归）

<,,,,,,,>

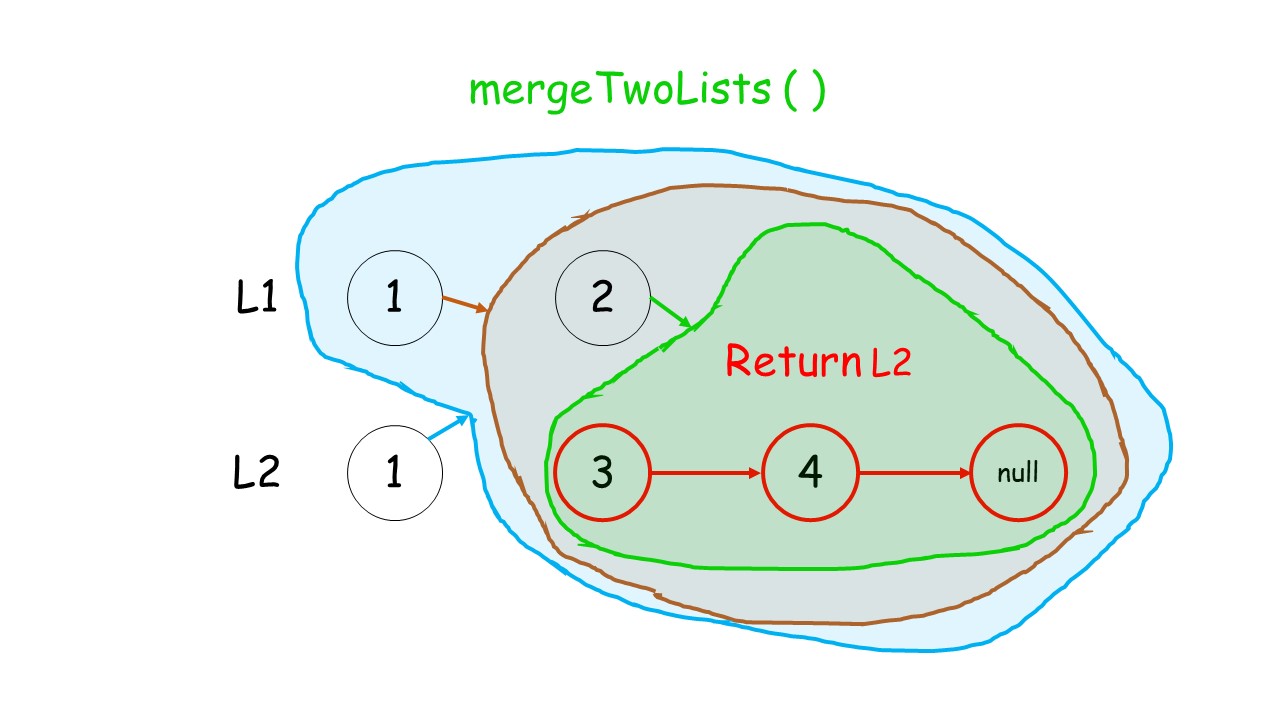
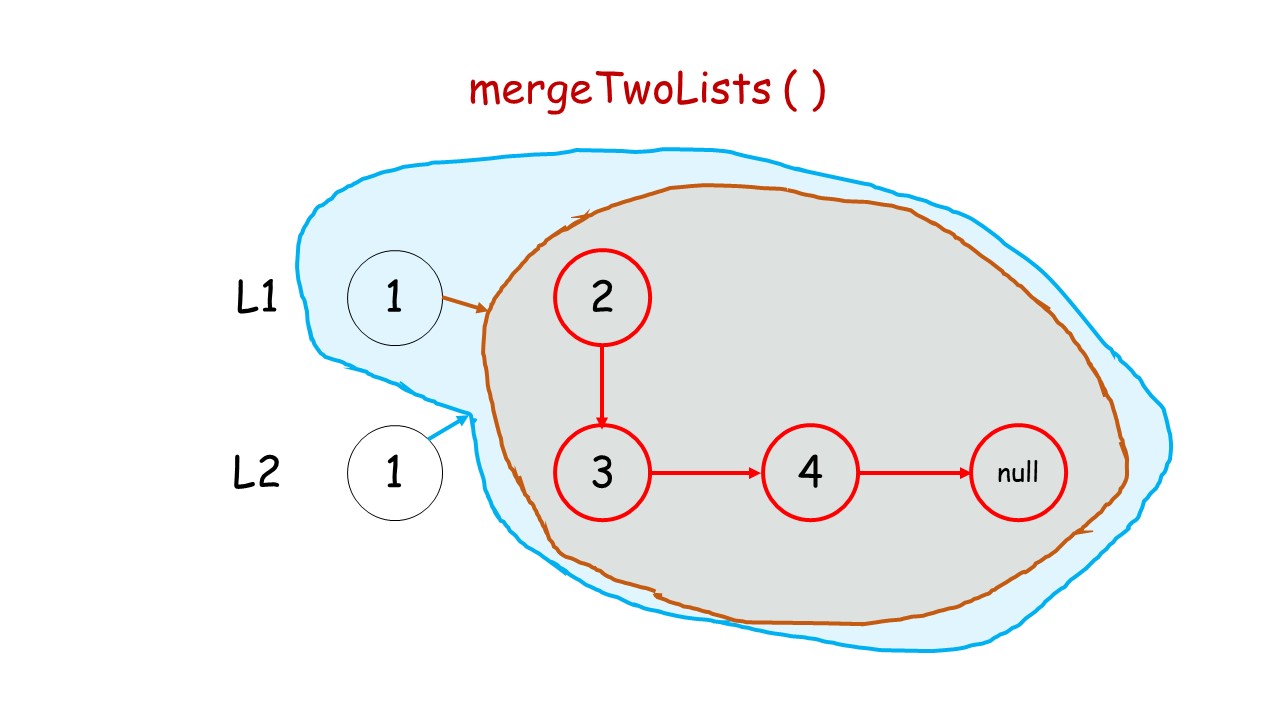
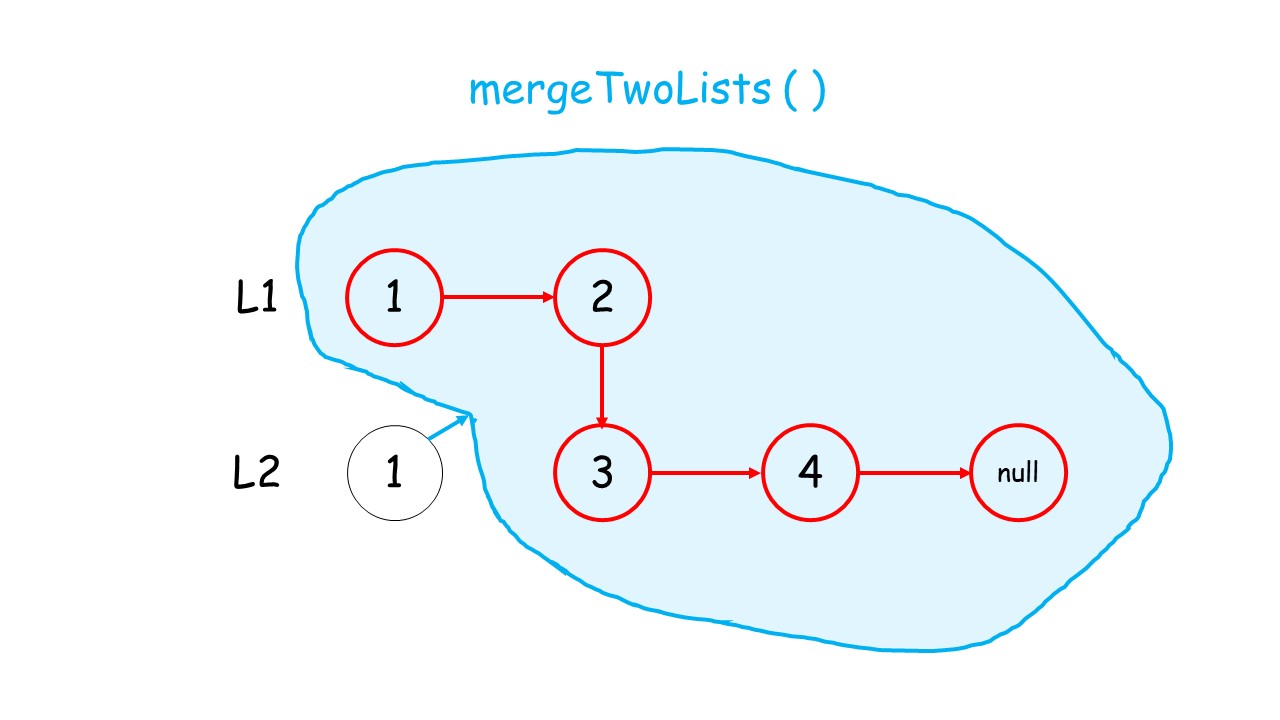
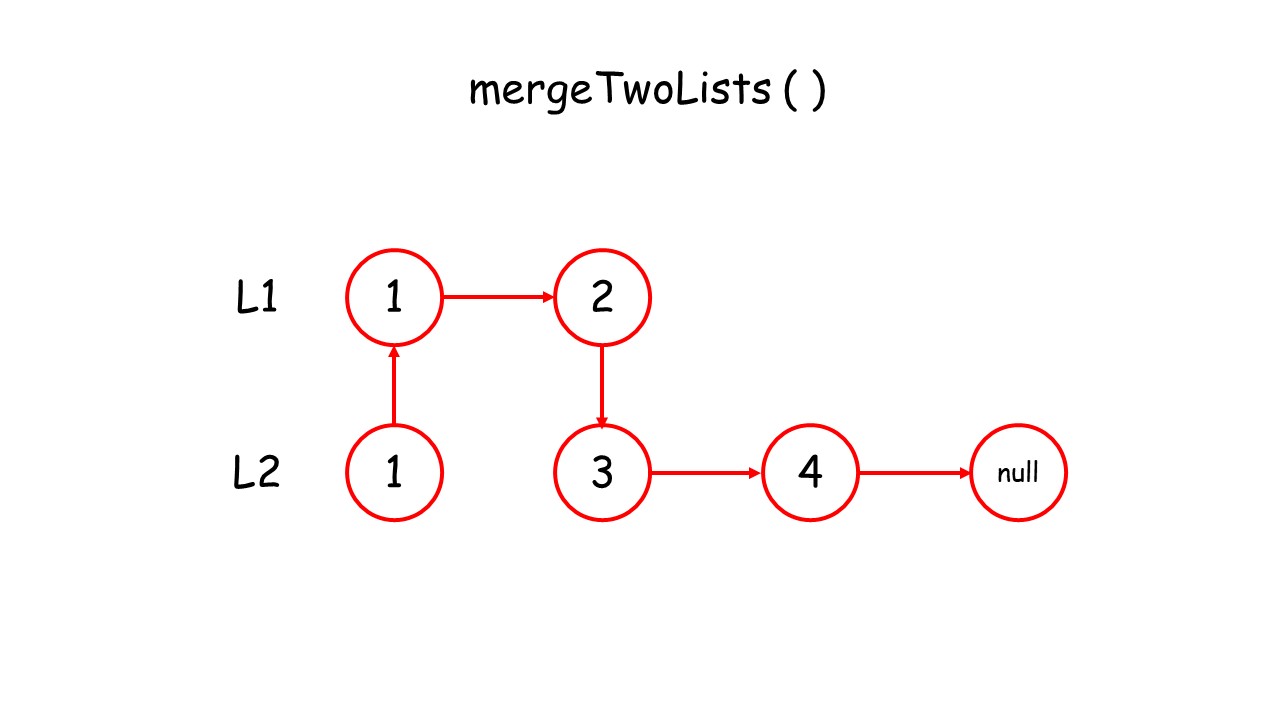
代码

感谢 @huwt 提供的 C++ 代码！

[]class Solution:
    def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
        if not l1: return l2  # 终止条件，直到两个链表都空
        if not l2: return l1
        if l1.val <= l2.val:  # 递归调用
            l1.next = self.mergeTwoLists(l1.next,l2)
            return l1
        else:
            l2.next = self.mergeTwoLists(l1,l2.next)
            return l2

[]class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        if (l1 == null) {
            return l2;
        }
        else if (l2 == null) {
            return l1;
        }
        else if (l1.val < l2.val) {
            l1.next = mergeTwoLists(l1.next, l2);
            return l1;
        }
        else {
            l2.next = mergeTwoLists(l1, l2.next);
            return l2;
        }

    }
}

[]class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        if (l1 == NULL) {
            return l2;
        }
        if (l2 == NULL) {
            return l1;
        }
        if (l1->val <= l2->val) {
            l1->next = mergeTwoLists(l1->next, l2);
            return l1;
        }
        l2->next = mergeTwoLists(l1, l2->next);
        return l2;
    }
};

复杂度分析

如何计算递归的时间复杂度和空间复杂度呢？力扣对此进行了详细介绍，其中时间复杂度可以这样计算：

给出一个递归算法，其时间复杂度 ${\mathcal{O}(T)}$ 通常是递归调用的数量（记作 ${R}$）和计算的时间复杂度的乘积（表示为 ${\mathcal{O}(s)}$）的乘积：${\mathcal{O}(T) = R * \mathcal{O}(s)}$

时间复杂度：${\mathcal{O}}(m + n)$。

$m$，$n$ 为 $l_{1}$ 和 $l_{2}$ 的元素个数。递归函数每次去掉一个元素，直到两个链表都为空，因此需要调用 $R=O(m + n)$ 次。而在递归函数中我们只进行了 next 指针的赋值操作，复杂度为 $\mathcal{O}(1)$，故递归的总时间复杂度为 ${\mathcal{O}(T) = R * \mathcal{O}(1)}={\mathcal{O}}(m + n)$ 。

空间复杂度：${\mathcal{O}}(m + n)$。**

对于递归调用 self.mergeTwoLists()，当它遇到终止条件准备回溯时，已经递归调用了 $m+n$ 次，使用了 $m+n$ 个栈帧，故最后的空间复杂度为 ${\mathcal{O}}(m + n)$。

0021-合并两个有序链表

1. 前言

2. 什么是递归？

3. 递归解法

代码

相关题目