给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例 1:
**输入:** lists = [[1,4,5],[1,3,4],[2,6]]
**输出:** [1,1,2,3,4,4,5,6]
**解释:** 链表数组如下:
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6
示例 2:
**输入:** lists = []
**输出:** []
示例 3:
**输入:** lists = [[]]
**输出:** []
提示:
k == lists.length0 <= k <= 10^40 <= lists[i].length <= 500-10^4 <= lists[i][j] <= 10^4lists[i] 按 升序 排列lists[i].length 的总和不超过 10^4
📺 视频题解

📖 文字题解
前置知识:合并两个有序链表
思路
在解决「合并K个排序链表」这个问题之前,我们先来看一个更简单的问题:如何合并两个有序链表?假设链表 $a$ 和 $b$ 的长度都是 $n$,如何在 $O(n)$ 的时间代价以及 $O(1)$ 的空间代价完成合并? 这个问题在面试中常常出现,为了达到空间代价是 $O(1)$,我们的宗旨是「原地调整链表元素的 $\textit{next}$ 指针完成合并」。以下是合并的步骤和注意事项,对这个问题比较熟悉的读者可以跳过这一部分。此部分建议结合代码阅读。
- 首先我们需要一个变量 $\textit{head}$ 来保存合并之后链表的头部,你可以把 $\textit{head}$ 设置为一个虚拟的头(也就是 $\textit{head}$ 的 $\textit{val}$ 属性不保存任何值),这是为了方便代码的书写,在整个链表合并完之后,返回它的下一位置即可。
- 我们需要一个指针 $\textit{tail}$ 来记录下一个插入位置的前一个位置,以及两个指针 $\textit{aPtr}$ 和 $\textit{bPtr}$ 来记录 $a$ 和 $b$ 未合并部分的第一位。注意这里的描述,$\textit{tail}$ 不是下一个插入的位置,$\textit{aPtr}$ 和 $\textit{bPtr}$ 所指向的元素处于「待合并」的状态,也就是说它们还没有合并入最终的链表。 当然你也可以给他们赋予其他的定义,但是定义不同实现就会不同。
- 当 $\textit{aPtr}$ 和 $\textit{bPtr}$ 都不为空的时候,取 $\textit{val}$ 属性较小的合并;如果 $\textit{aPtr}$ 为空,则把整个 $\textit{bPtr}$ 以及后面的元素全部合并;$\textit{bPtr}$ 为空时同理。
- 在合并的时候,应该先调整 $\textit{tail}$ 的 $\textit{next}$ 属性,再后移 $\textit{tail}$ 和 $\textit{*Ptr}$($\textit{aPtr}$ 或者 $\textit{bPtr}$)。那么这里 $\textit{tail}$ 和 $\textit{*Ptr}$ 是否存在先后顺序呢?它们谁先动谁后动都是一样的,不会改变任何元素的 $\textit{next}$ 指针。
代码
[pre-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
| ListNode* mergeTwoLists(ListNode *a, ListNode *b) {
if ((!a) || (!b)) return a ? a : b;
ListNode head, *tail = &head, *aPtr = a, *bPtr = b;
while (aPtr && bPtr) {
if (aPtr->val < bPtr->val) {
tail->next = aPtr; aPtr = aPtr->next;
} else {
tail->next = bPtr; bPtr = bPtr->next;
}
tail = tail->next;
}
tail->next = (aPtr ? aPtr : bPtr);
return head.next;
}
|
[pre-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| public ListNode mergeTwoLists(ListNode a, ListNode b) {
if (a == null || b == null) {
return a != null ? a : b;
}
ListNode head = new ListNode(0);
ListNode tail = head, aPtr = a, bPtr = b;
while (aPtr != null && bPtr != null) {
if (aPtr.val < bPtr.val) {
tail.next = aPtr;
aPtr = aPtr.next;
} else {
tail.next = bPtr;
bPtr = bPtr.next;
}
tail = tail.next;
}
tail.next = (aPtr != null ? aPtr : bPtr);
return head.next;
}
|
复杂度分析
- 时间复杂度:$O(n)$。
- 空间复杂度:$O(1)$。
方法一:顺序合并
思路
我们可以想到一种最朴素的方法:用一个变量 $\textit{ans}$ 来维护以及合并的链表,第 $i$ 次循环把第 $i$ 个链表和 $\textit{ans}$ 合并,答案保存到 $\textit{ans}$ 中。
代码
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution {
public:
ListNode* mergeTwoLists(ListNode *a, ListNode *b) {
if ((!a) || (!b)) return a ? a : b;
ListNode head, *tail = &head, *aPtr = a, *bPtr = b;
while (aPtr && bPtr) {
if (aPtr->val < bPtr->val) {
tail->next = aPtr; aPtr = aPtr->next;
} else {
tail->next = bPtr; bPtr = bPtr->next;
}
tail = tail->next;
}
tail->next = (aPtr ? aPtr : bPtr);
return head.next;
}
ListNode* mergeKLists(vector<ListNode*>& lists) {
ListNode *ans = nullptr;
for (size_t i = 0; i < lists.size(); ++i) {
ans = mergeTwoLists(ans, lists[i]);
}
return ans;
}
};
|
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| class Solution {
public ListNode mergeKLists(ListNode[] lists) {
ListNode ans = null;
for (int i = 0; i < lists.length; ++i) {
ans = mergeTwoLists(ans, lists[i]);
}
return ans;
}
public ListNode mergeTwoLists(ListNode a, ListNode b) {
if (a == null || b == null) {
return a != null ? a : b;
}
ListNode head = new ListNode(0);
ListNode tail = head, aPtr = a, bPtr = b;
while (aPtr != null && bPtr != null) {
if (aPtr.val < bPtr.val) {
tail.next = aPtr;
aPtr = aPtr.next;
} else {
tail.next = bPtr;
bPtr = bPtr.next;
}
tail = tail.next;
}
tail.next = (aPtr != null ? aPtr : bPtr);
return head.next;
}
}
|
复杂度分析
- 时间复杂度:假设每个链表的最长长度是 $n$。在第一次合并后,$\textit{ans}$ 的长度为 $n$;第二次合并后,$\textit{ans}$ 的长度为 $2\times n$,第 $i$ 次合并后,$\textit{ans}$ 的长度为 $i\times n$。第 $i$ 次合并的时间代价是 $O(n + (i - 1) \times n) = O(i \times n)$,那么总的时间代价为 $O(\sum_{i = 1}^{k} (i \times n)) = O(\frac{(1 + k)\cdot k}{2} \times n) = O(k^2 n)$,故渐进时间复杂度为 $O(k^2 n)$。
- 空间复杂度:没有用到与 $k$ 和 $n$ 规模相关的辅助空间,故渐进空间复杂度为 $O(1)$。
方法二:分治合并
思路
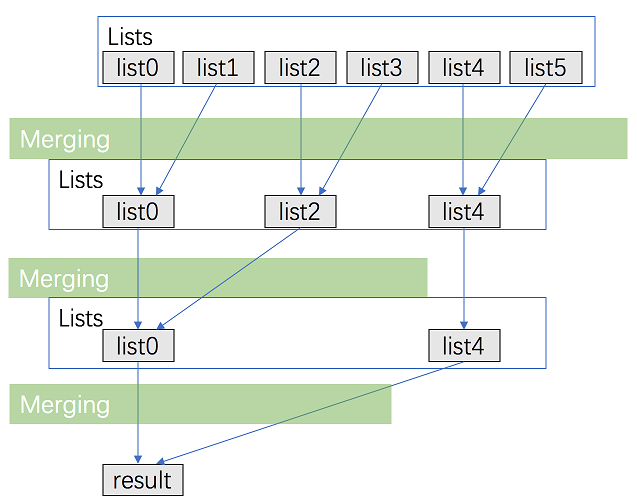
考虑优化方法一,用分治的方法进行合并。
- 将 $k$ 个链表配对并将同一对中的链表合并;
- 第一轮合并以后, $k$ 个链表被合并成了 $\frac{k}{2}$ 个链表,平均长度为 $\frac{2n}{k}$,然后是 $\frac{k}{4}$ 个链表, $\frac{k}{8}$ 个链表等等;
- 重复这一过程,直到我们得到了最终的有序链表。

代码
[sol2-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public:
ListNode* mergeTwoLists(ListNode *a, ListNode *b) {
if ((!a) || (!b)) return a ? a : b;
ListNode head, *tail = &head, *aPtr = a, *bPtr = b;
while (aPtr && bPtr) {
if (aPtr->val < bPtr->val) {
tail->next = aPtr; aPtr = aPtr->next;
} else {
tail->next = bPtr; bPtr = bPtr->next;
}
tail = tail->next;
}
tail->next = (aPtr ? aPtr : bPtr);
return head.next;
}
ListNode* merge(vector <ListNode*> &lists, int l, int r) {
if (l == r) return lists[l];
if (l > r) return nullptr;
int mid = (l + r) >> 1;
return mergeTwoLists(merge(lists, l, mid), merge(lists, mid + 1, r));
}
ListNode* mergeKLists(vector<ListNode*>& lists) {
return merge(lists, 0, lists.size() - 1);
}
};
|
[sol2-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| class Solution {
public ListNode mergeKLists(ListNode[] lists) {
return merge(lists, 0, lists.length - 1);
}
public ListNode merge(ListNode[] lists, int l, int r) {
if (l == r) {
return lists[l];
}
if (l > r) {
return null;
}
int mid = (l + r) >> 1;
return mergeTwoLists(merge(lists, l, mid), merge(lists, mid + 1, r));
}
public ListNode mergeTwoLists(ListNode a, ListNode b) {
if (a == null || b == null) {
return a != null ? a : b;
}
ListNode head = new ListNode(0);
ListNode tail = head, aPtr = a, bPtr = b;
while (aPtr != null && bPtr != null) {
if (aPtr.val < bPtr.val) {
tail.next = aPtr;
aPtr = aPtr.next;
} else {
tail.next = bPtr;
bPtr = bPtr.next;
}
tail = tail.next;
}
tail.next = (aPtr != null ? aPtr : bPtr);
return head.next;
}
}
|
复杂度分析
- 时间复杂度:考虑递归「向上回升」的过程——第一轮合并 $\frac{k}{2}$ 组链表,每一组的时间代价是 $O(2n)$;第二轮合并 $\frac{k}{4}$ 组链表,每一组的时间代价是 $O(4n)$……所以总的时间代价是 $O(\sum_{i = 1}^{\infty} \frac{k}{2^i} \times 2^i n) = O(kn \times \log k)$,故渐进时间复杂度为 $O(kn \times \log k)$。
- 空间复杂度:递归会使用到 $O(\log k)$ 空间代价的栈空间。
方法三:使用优先队列合并
思路
这个方法和前两种方法的思路有所不同,我们需要维护当前每个链表没有被合并的元素的最前面一个,$k$ 个链表就最多有 $k$ 个满足这样条件的元素,每次在这些元素里面选取 $\textit{val}$ 属性最小的元素合并到答案中。在选取最小元素的时候,我们可以用优先队列来优化这个过程。
代码
[sol3-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class Solution {
public:
struct Status {
int val;
ListNode *ptr;
bool operator < (const Status &rhs) const {
return val > rhs.val;
}
};
priority_queue <Status> q;
ListNode* mergeKLists(vector<ListNode*>& lists) {
for (auto node: lists) {
if (node) q.push({node->val, node});
}
ListNode head, *tail = &head;
while (!q.empty()) {
auto f = q.top(); q.pop();
tail->next = f.ptr;
tail = tail->next;
if (f.ptr->next) q.push({f.ptr->next->val, f.ptr->next});
}
return head.next;
}
};
|
[sol3-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| class Solution {
class Status implements Comparable<Status> {
int val;
ListNode ptr;
Status(int val, ListNode ptr) {
this.val = val;
this.ptr = ptr;
}
public int compareTo(Status status2) {
return this.val - status2.val;
}
}
PriorityQueue<Status> queue = new PriorityQueue<Status>();
public ListNode mergeKLists(ListNode[] lists) {
for (ListNode node: lists) {
if (node != null) {
queue.offer(new Status(node.val, node));
}
}
ListNode head = new ListNode(0);
ListNode tail = head;
while (!queue.isEmpty()) {
Status f = queue.poll();
tail.next = f.ptr;
tail = tail.next;
if (f.ptr.next != null) {
queue.offer(new Status(f.ptr.next.val, f.ptr.next));
}
}
return head.next;
}
}
|
复杂度分析
- 时间复杂度:考虑优先队列中的元素不超过 $k$ 个,那么插入和删除的时间代价为 $O(\log k)$,这里最多有 $kn$ 个点,对于每个点都被插入删除各一次,故总的时间代价即渐进时间复杂度为 $O(kn \times \log k)$。
- 空间复杂度:这里用了优先队列,优先队列中的元素不超过 $k$ 个,故渐进空间复杂度为 $O(k)$。