0031-下一个排列
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
- 例如,
arr = [1,2,3],以下这些都可以视作arr的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1]。
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的
下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
- 例如,
arr = [1,2,3]的下一个排列是[1,3,2]。 - 类似地,
arr = [2,3,1]的下一个排列是[3,1,2]。 - 而
arr = [3,2,1]的下一个排列是[1,2,3],因为[3,2,1]不存在一个字典序更大的排列。
给你一个整数数组 nums ,找出 nums 的下一个排列。
必须 原地
修改,只允许使用额外常数空间。
示例 1:
**输入:** nums = [1,2,3]
**输出:** [1,3,2]
示例 2:
**输入:** nums = [3,2,1]
**输出:** [1,2,3]
示例 3:
**输入:** nums = [1,1,5]
**输出:** [1,5,1]
提示:
1 <= nums.length <= 1000 <= nums[i] <= 100
下一个排列
问题描述
这道题是 LeetCode 31题 。
“下一个排列” 的定义是:给定数字序列的字典序中下一个更大的排列。如果不存在下一个更大的排列,则将数字重新排列成最小的排列(即升序排列)。
我们可以将该问题形式化地描述为:给定若干个数字,将其组合为一个整数。如何将这些数字重新排列,以得到下一个更大的整数。如 123 下一个更大的数为 132。如果没有更大的整数,则输出最小的整数。
以 1,2,3,4,5,6 为例,其排列依次为:
1 | 123456 |
可以看到有这样的关系:123456 < 123465 < 123546 < ... < 654321。
算法推导
如何得到这样的排列顺序?这是本文的重点。我们可以这样来分析:
- 我们希望下一个数 比当前数大,这样才满足 “下一个排列” 的定义。因此只需要 将后面的「大数」与前面的「小数」交换,就能得到一个更大的数。比如
123456,将5和6交换就能得到一个更大的数123465。 - 我们还希望下一个数 增加的幅度尽可能的小,这样才满足“下一个排列与当前排列紧邻“的要求。为了满足这个要求,我们需要:
- 在 尽可能靠右的低位 进行交换,需要 从后向前 查找
- 将一个 尽可能小的「大数」 与前面的「小数」交换。比如
123465,下一个排列应该把5和4交换而不是把6和4交换 - 将「大数」换到前面后,需要将「大数」后面的所有数 重置为升序,升序排列就是最小的排列。以
123465为例:首先按照上一步,交换5和4,得到123564;然后需要将5之后的数重置为升序,得到123546。显然123546比123564更小,123546就是123465的下一个排列
以上就是求 “下一个排列” 的分析过程。
算法过程
标准的 “下一个排列” 算法可以描述为:
- 从后向前 查找第一个 相邻升序 的元素对
(i,j),满足A[i] < A[j]。此时[j,end)必然是降序 - 在
[j,end)从后向前 查找第一个满足A[i] < A[k]的k。A[i]、A[k]分别就是上文所说的「小数」、「大数」 - 将
A[i]与A[k]交换 - 可以断定这时
[j,end)必然是降序,逆置[j,end),使其升序 - 如果在步骤 1 找不到符合的相邻元素对,说明当前
[begin,end)为一个降序顺序,则直接跳到步骤 4
该方法支持数据重复,且在 C++ STL 中被采用。
代码
1 | func nextPermutation(nums []int) { |
可视化
以求 12385764 的下一个排列为例: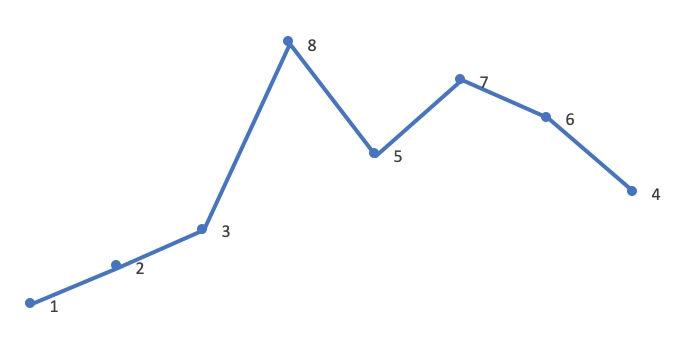
首先从后向前查找第一个相邻升序的元素对 (i,j)。这里 i=4,j=5,对应的值为 5,7: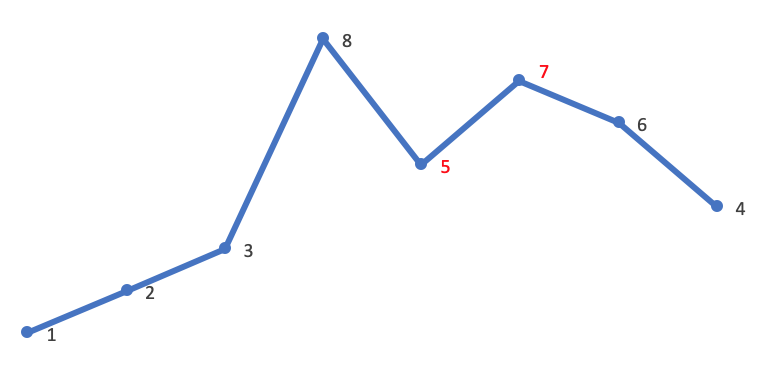
然后在 [j,end) 从后向前查找第一个大于 A[i] 的值 A[k]。这里 A[i] 是 5,故 A[k] 是 6: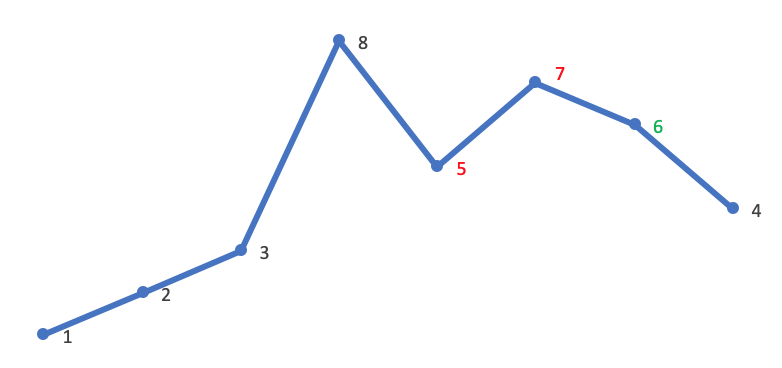
将 A[i] 与 A[k] 交换。这里交换 5、6: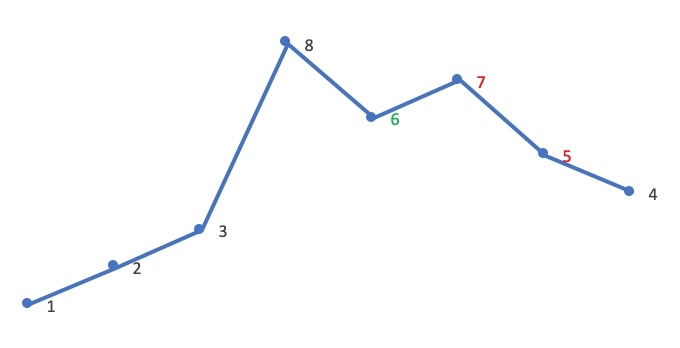
这时 [j,end) 必然是降序,逆置 [j,end),使其升序。这里逆置 [7,5,4]: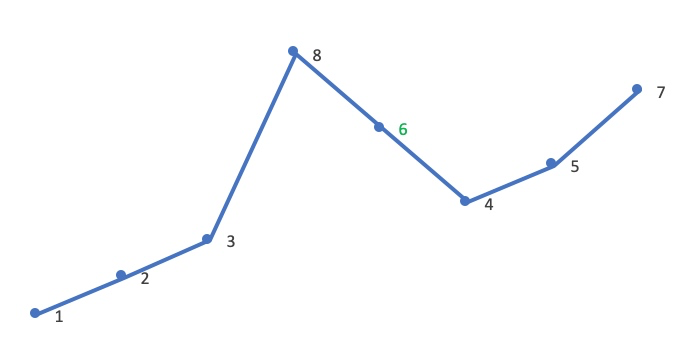
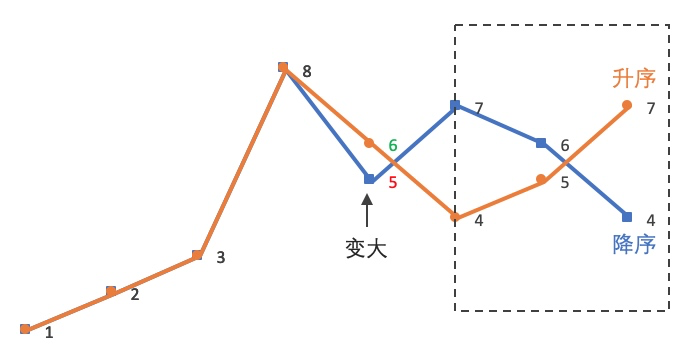
因此,12385764 的下一个排列就是 12386457。
最后再可视化地对比一下这两个相邻的排列(橙色是蓝色的下一个排列):