0035-搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
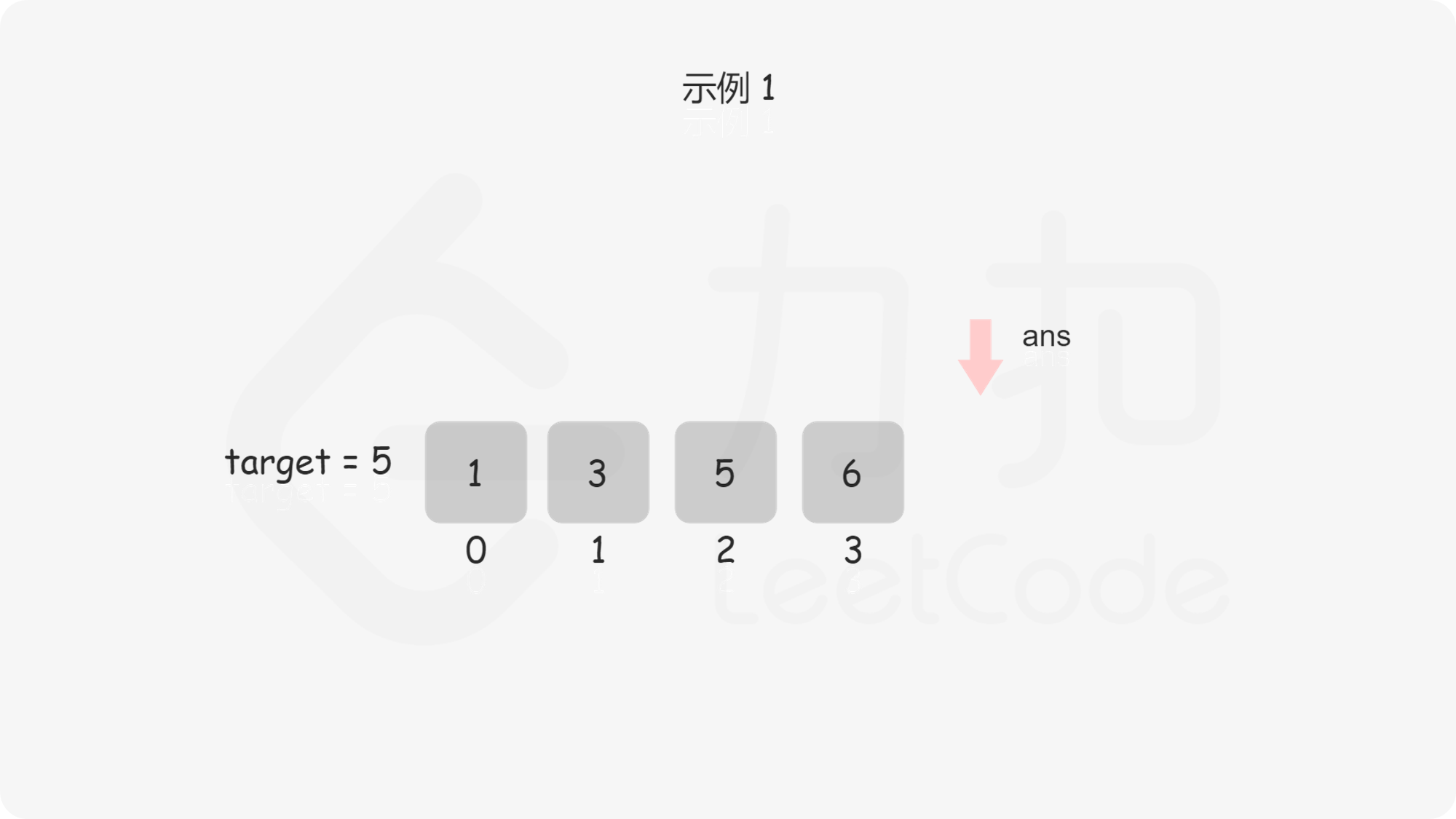
**输入:** nums = [1,3,5,6], target = 5
**输出:** 2
示例 2:
**输入:** nums = [1,3,5,6], target = 2
**输出:** 1
示例 3:
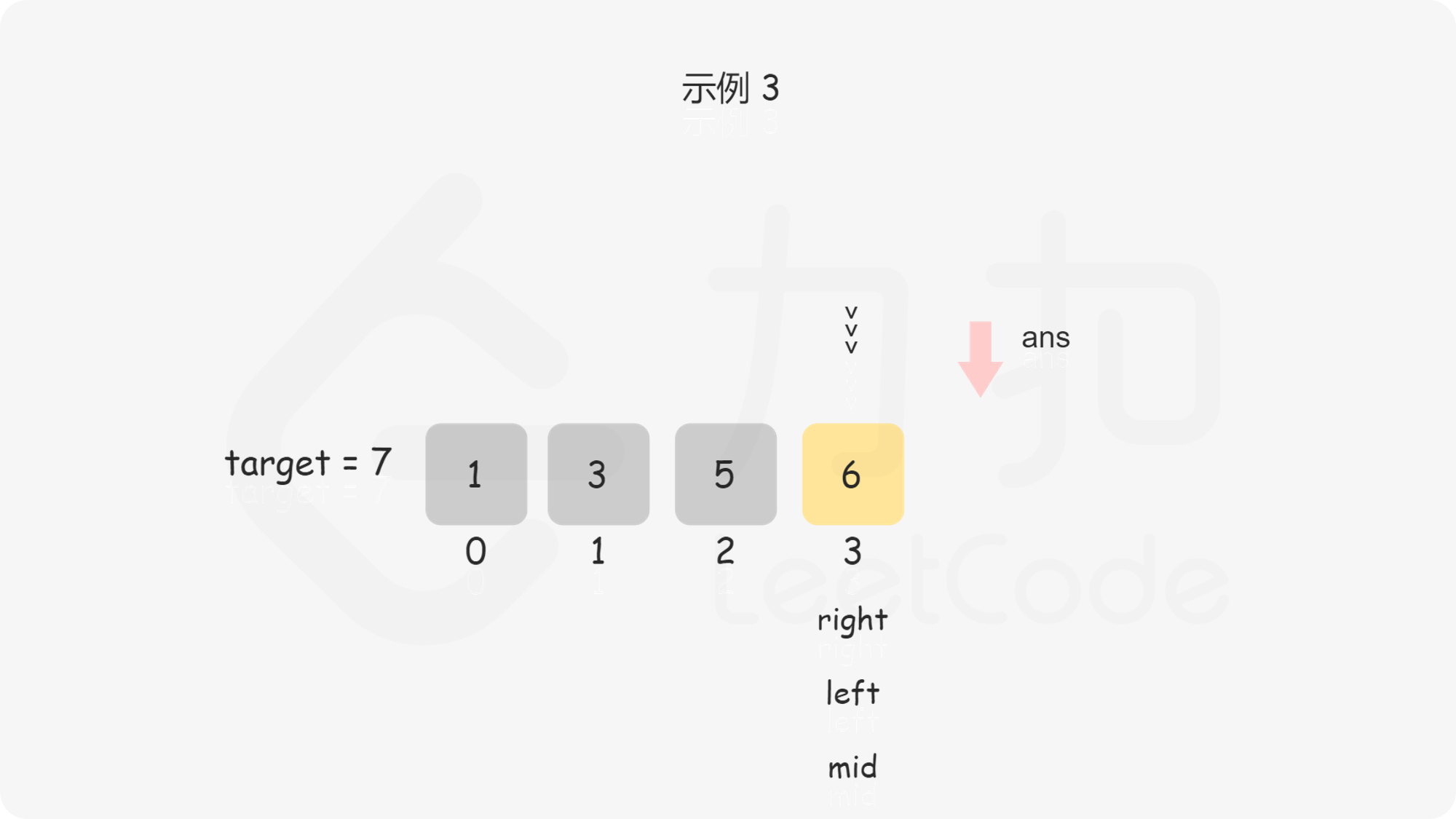
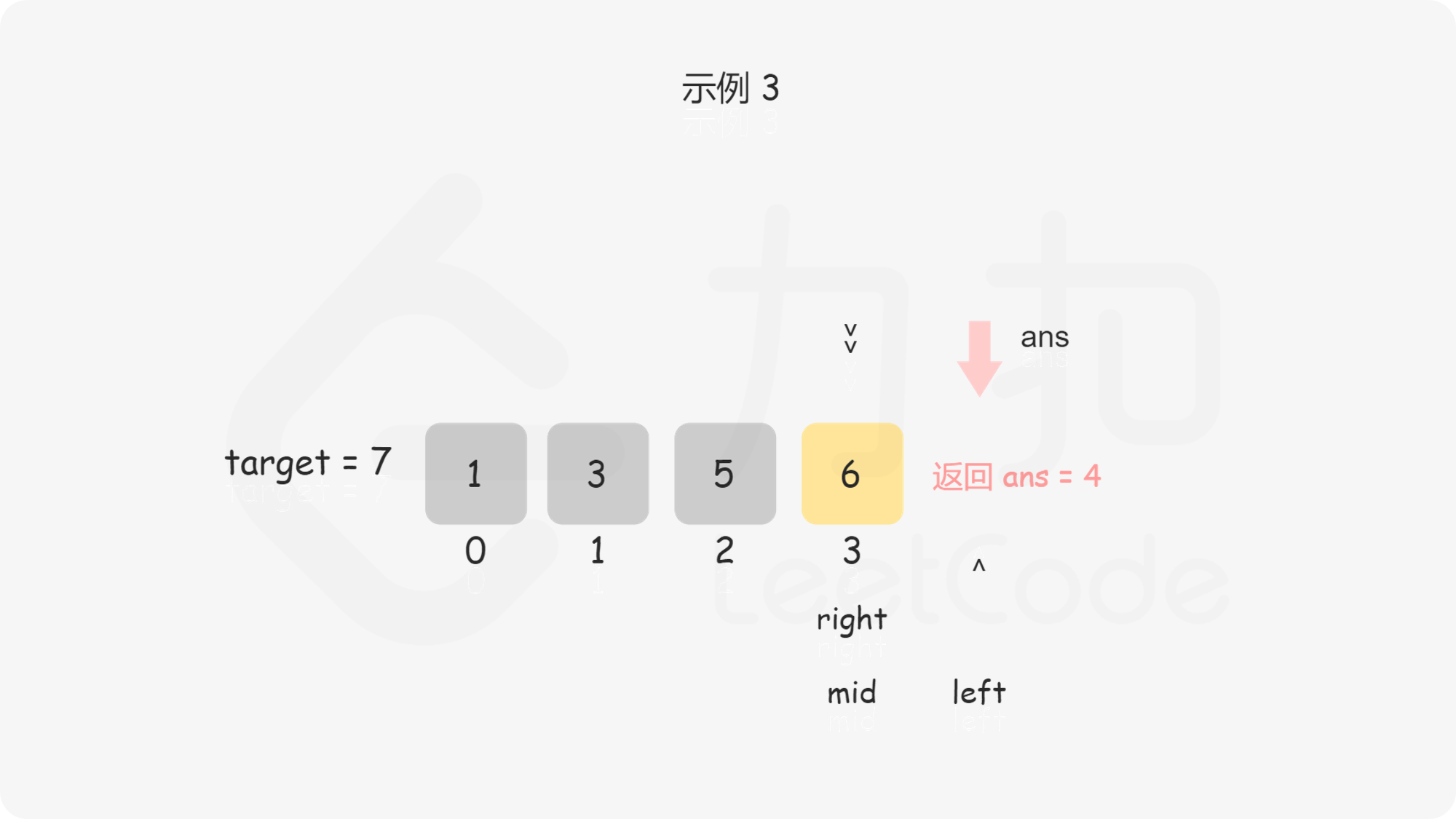
**输入:** nums = [1,3,5,6], target = 7
**输出:** 4
提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums为 **无重复元素 **的 **升序 **排列数组-104 <= target <= 104
📺 视频题解
📖 文字题解
方法一:二分查找
思路与算法
假设题意是叫你在排序数组中寻找是否存在一个目标值,那么训练有素的读者肯定立马就能想到利用二分法在 $O(\log n)$ 的时间内找到是否存在目标值。但这题还多了个额外的条件,即如果不存在数组中的时候需要返回按顺序插入的位置,那我们还能用二分法么?答案是可以的,我们只需要稍作修改即可。
考虑这个插入的位置 $\textit{pos}$,它成立的条件为:
$$
\textit{nums}[pos-1]<\textit{target}\le \textit{nums}[pos]
$$
其中 $\textit{nums}$ 代表排序数组。由于如果存在这个目标值,我们返回的索引也是 $\textit{pos}$,因此我们可以将两个条件合并得出最后的目标:「在一个有序数组中找第一个大于等于 $\textit{target}$ 的下标」。
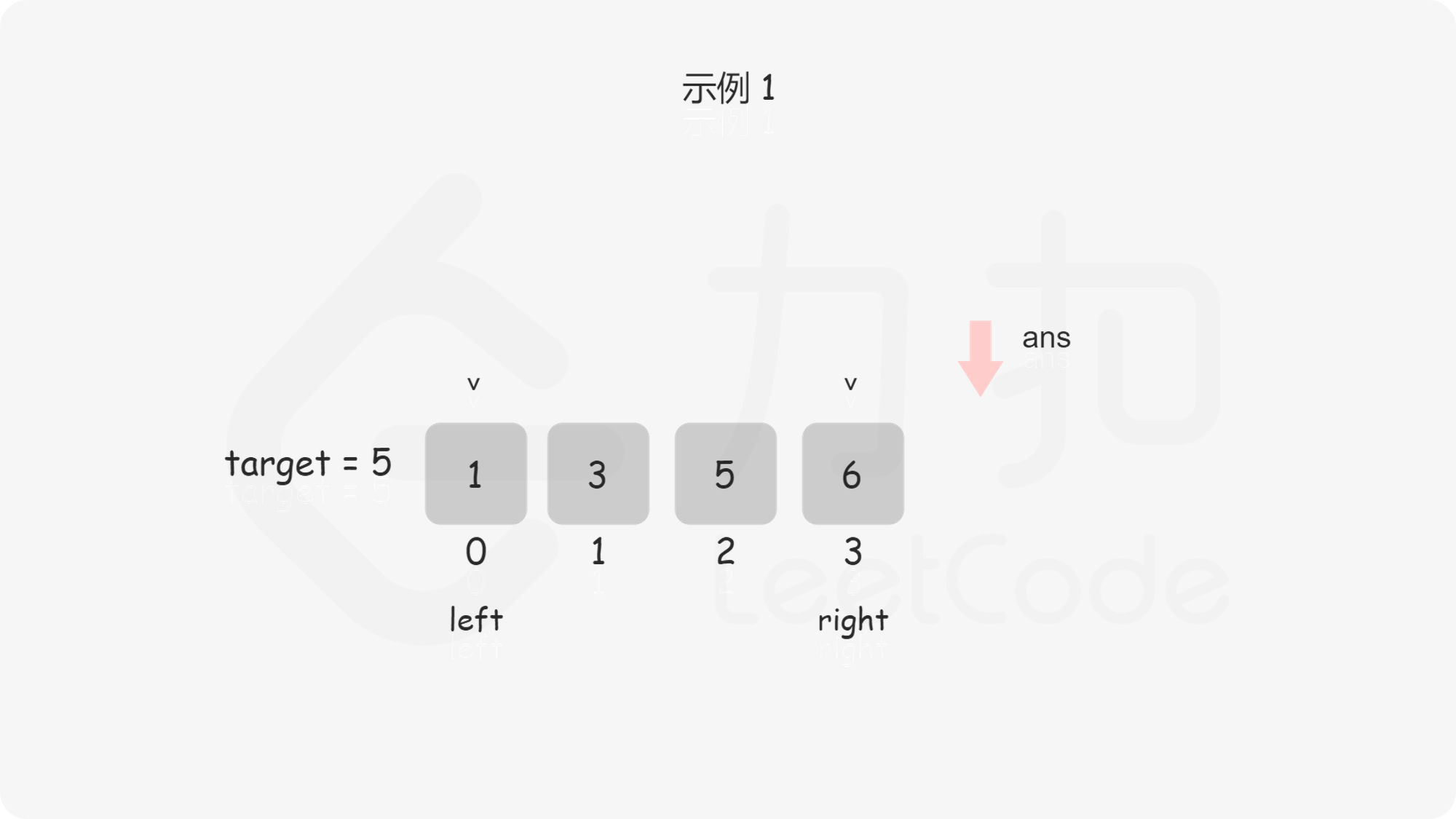
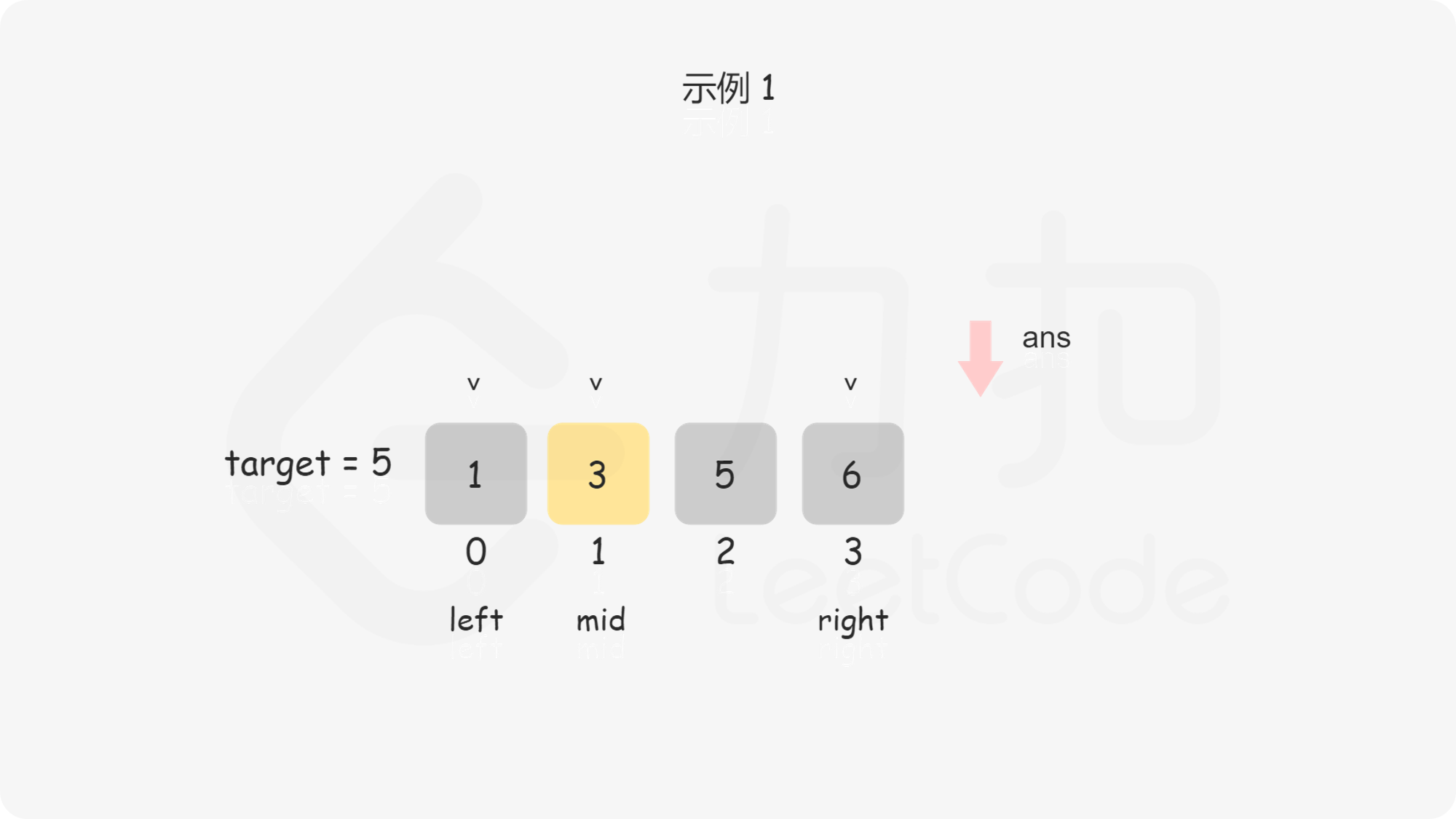
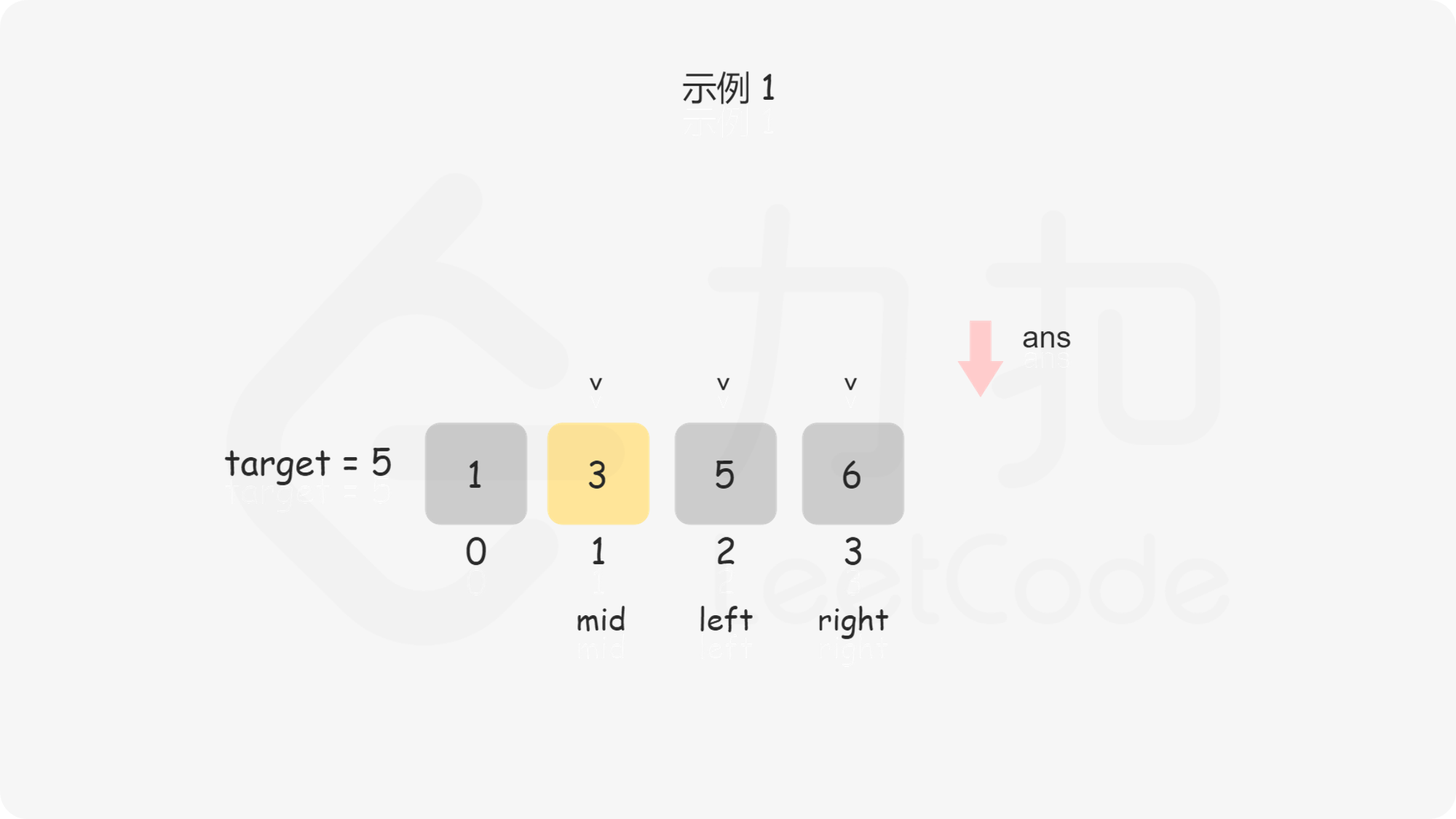
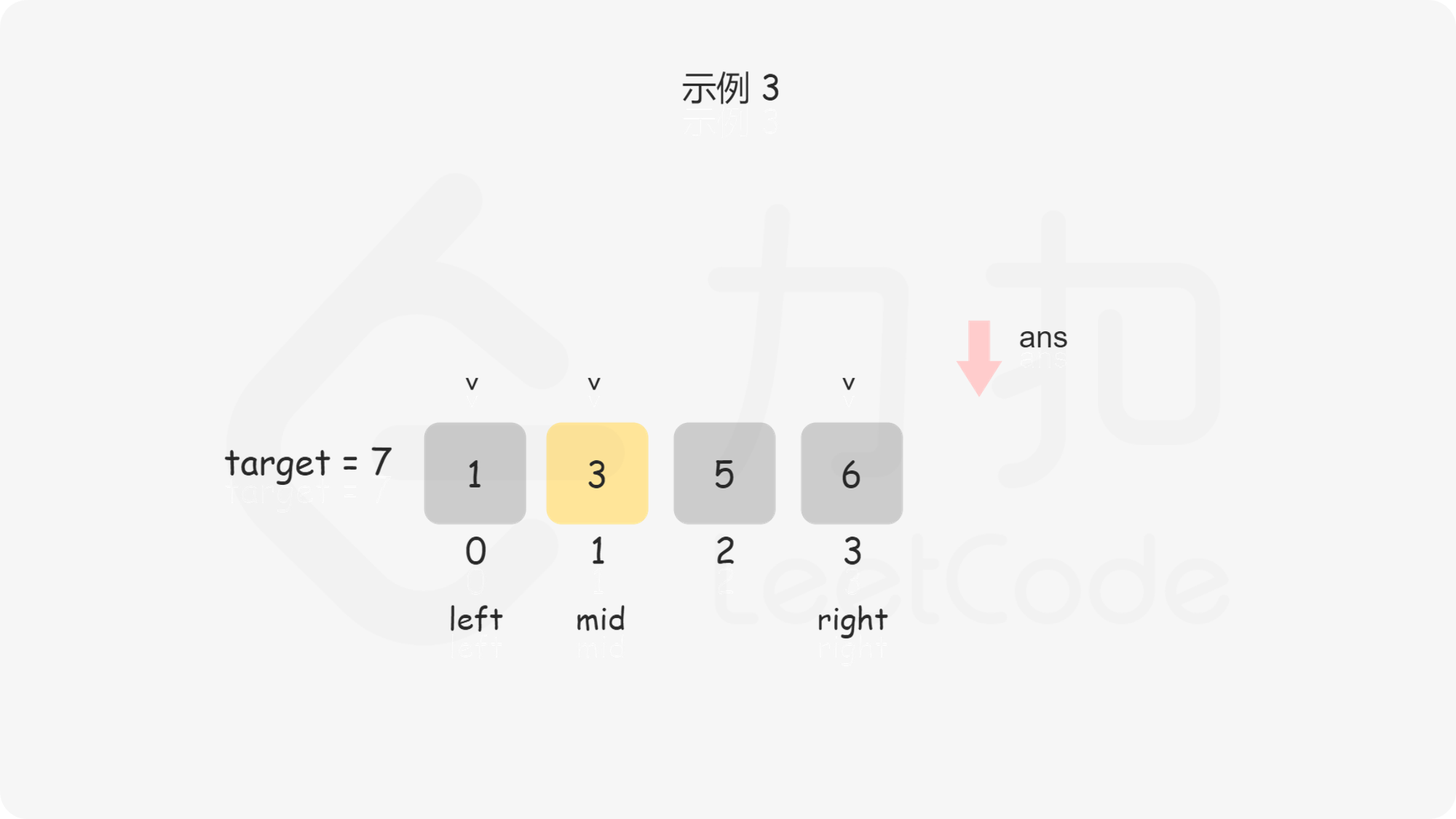
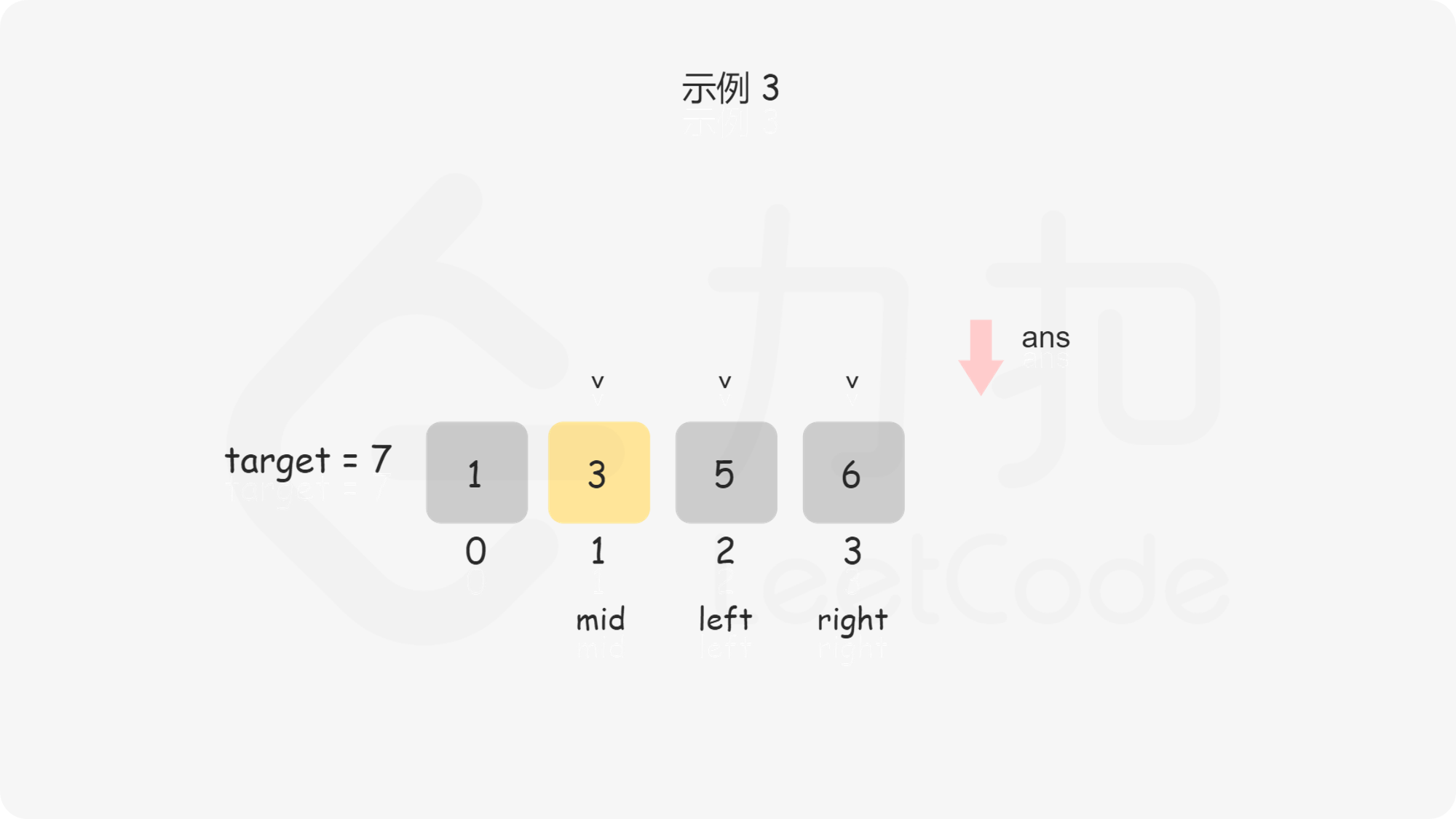
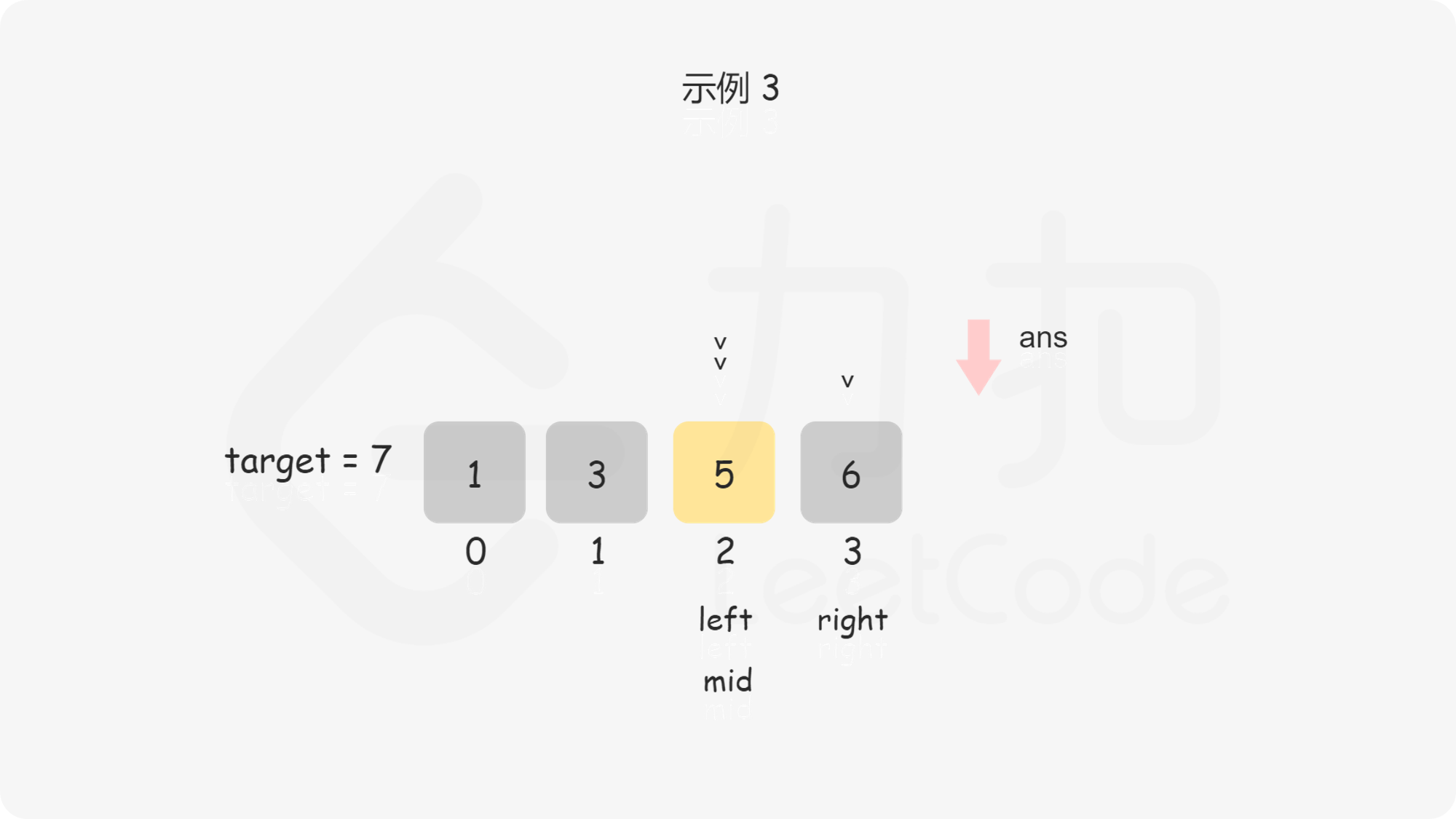
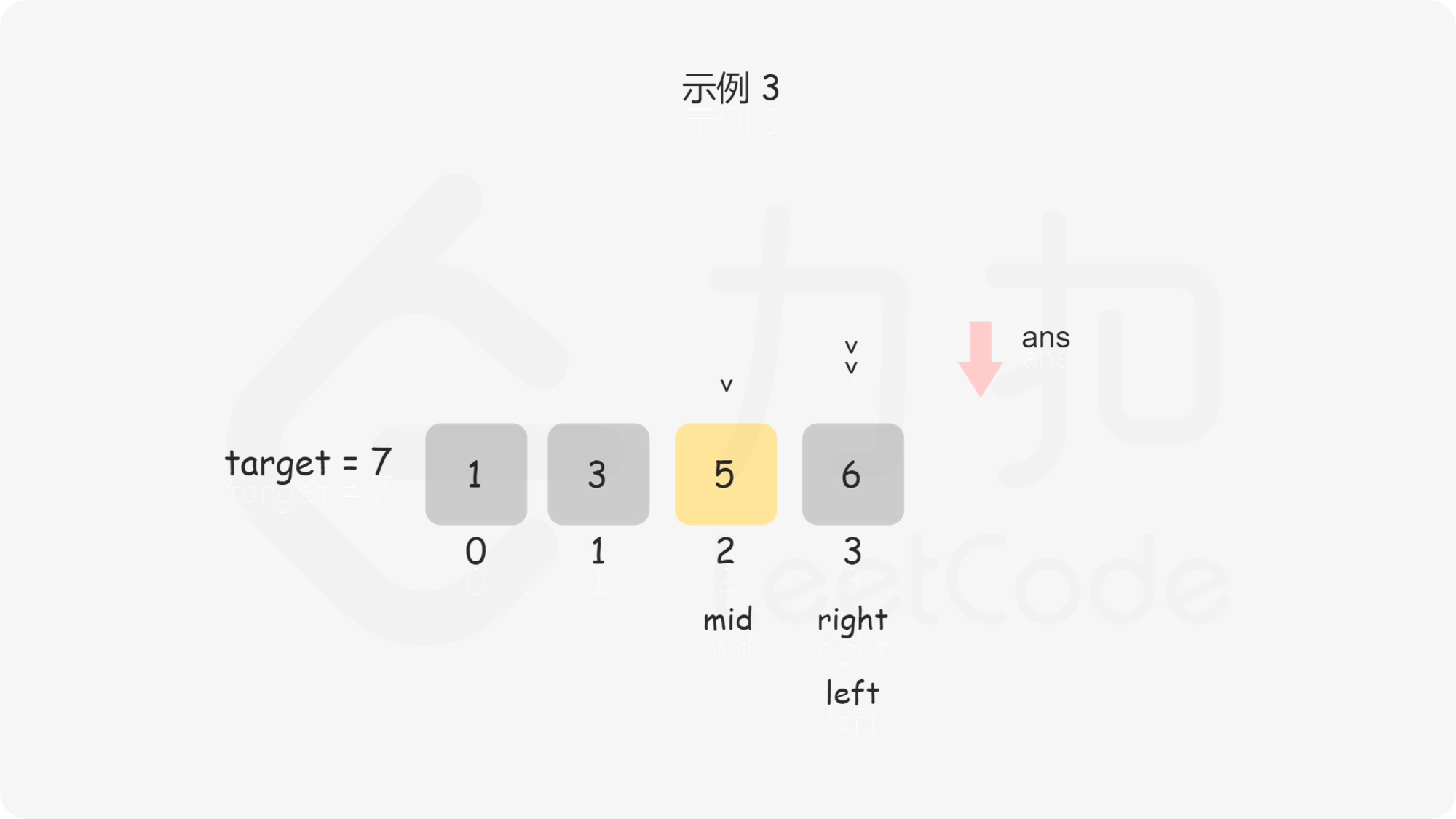
问题转化到这里,直接套用二分法即可,即不断用二分法逼近查找第一个大于等于 $\textit{target}$ 的下标 。下文给出的代码是笔者习惯的二分写法,$\textit{ans}$ 初值设置为数组长度可以省略边界条件的判断,因为存在一种情况是 $\textit{target}$ 大于数组中的所有数,此时需要插入到数组长度的位置。
< ,
, ,
, ,
, ,
,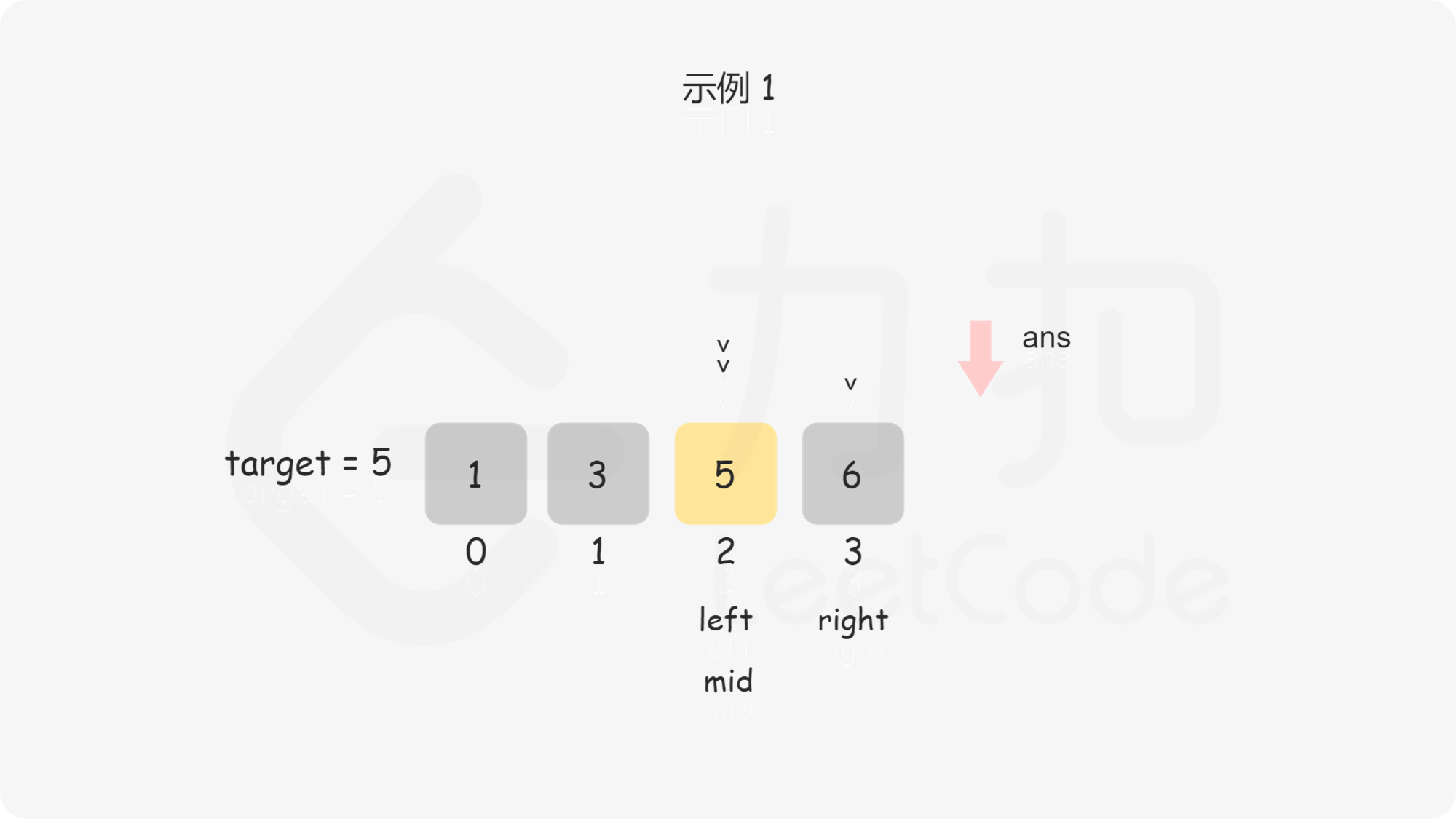 ,
,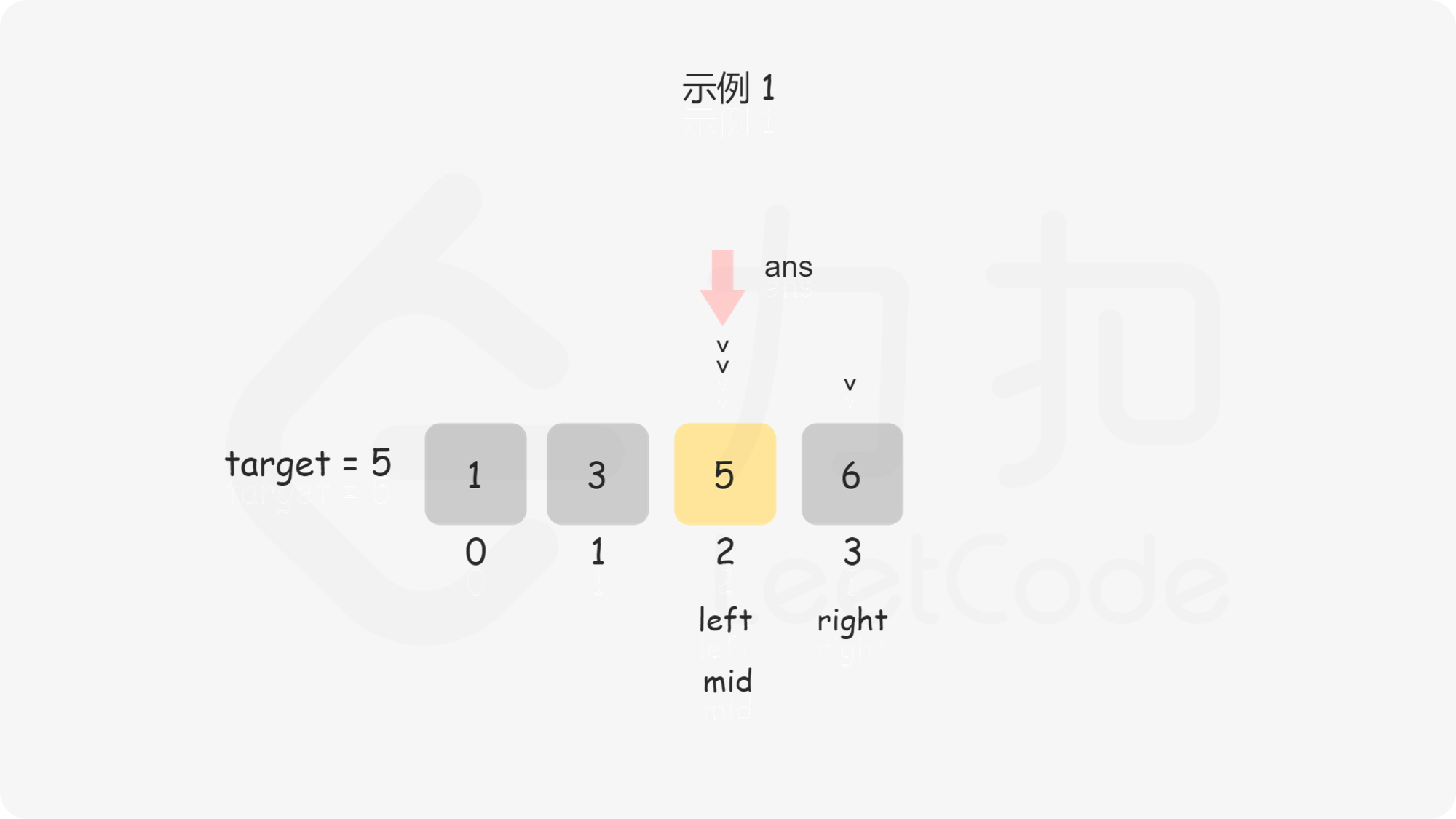 ,
,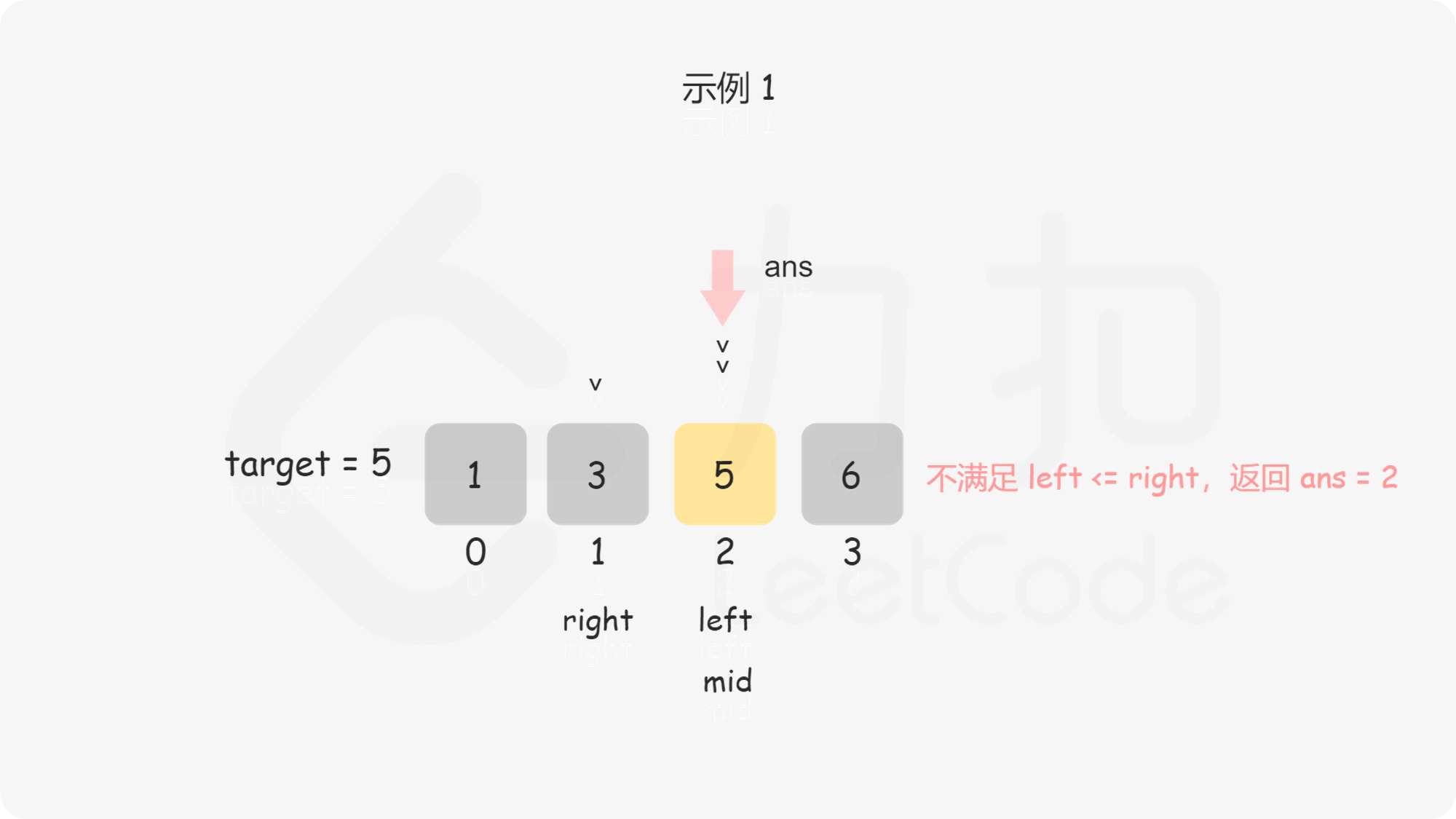 ,
, ,
,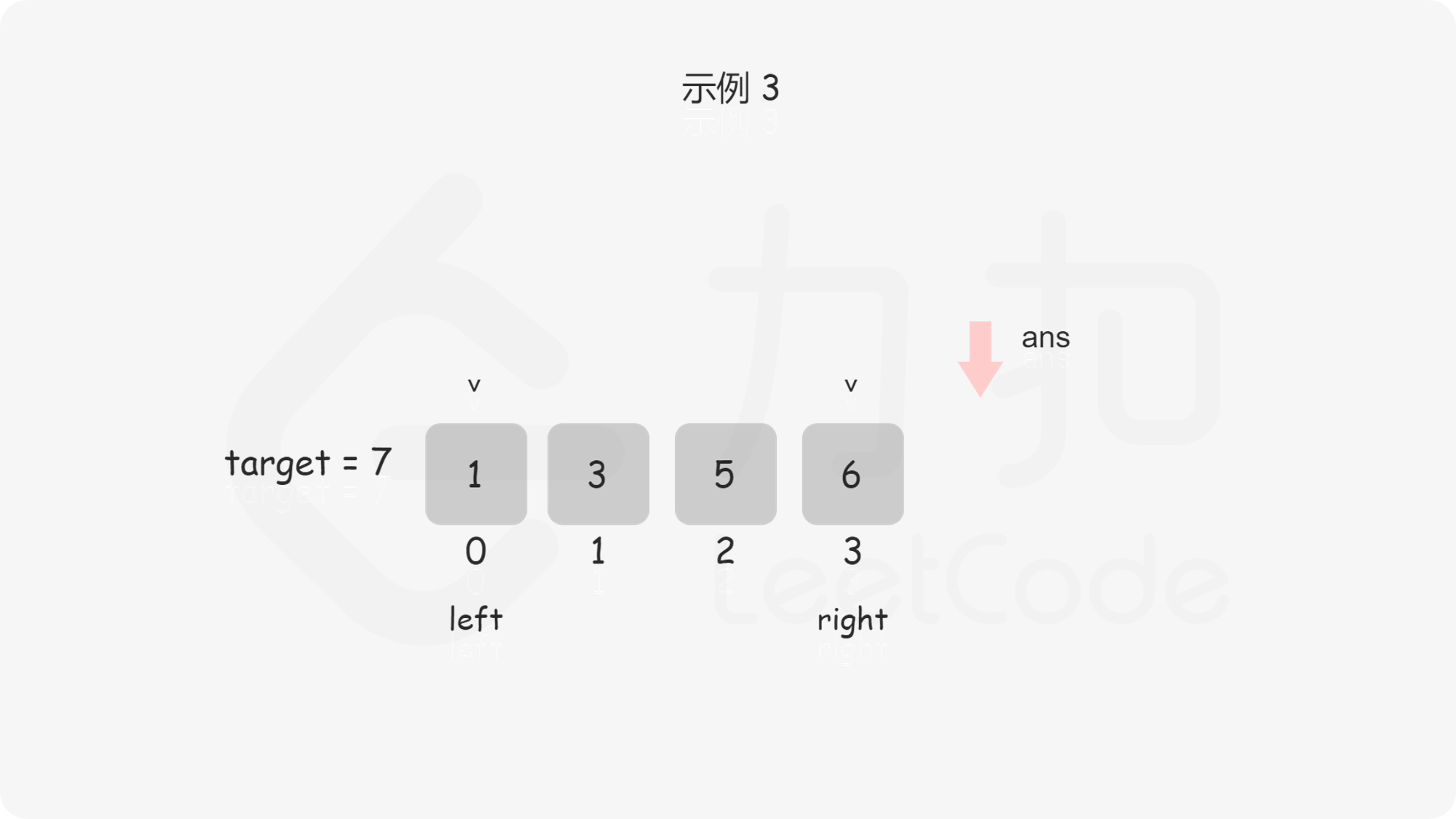 ,
, ,
, ,
, ,
, ,
, ,
, >
>
1 | class Solution { |
1 | class Solution { |
1 | var searchInsert = function(nums, target) { |
1 | int searchInsert(int* nums, int numsSize, int target) { |
1 | func searchInsert(nums []int, target int) int { |
复杂度分析
时间复杂度:$O(\log n)$,其中 $n$ 为数组的长度。二分查找所需的时间复杂度为 $O(\log n)$。
空间复杂度:$O(1)$。我们只需要常数空间存放若干变量。
Comments
