给你一个 无重叠的 , 按照区间起始端点排序的区间列表。
在列表中插入一个新的区间,你需要确保列表中的区间仍然有序且不重叠(如果有必要的话,可以合并区间)。
示例 1:
**输入:** intervals = [[1,3],[6,9]], newInterval = [2,5]
**输出:** [[1,5],[6,9]]
示例 2:
**输入:** intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]
**输出:** [[1,2],[3,10],[12,16]]
**解释:** 这是因为新的区间 [4,8] 与 [3,5],[6,7],[8,10] 重叠。
示例 3:
**输入:** intervals = [], newInterval = [5,7]
**输出:** [[5,7]]
示例 4:
**输入:** intervals = [[1,5]], newInterval = [2,3]
**输出:** [[1,5]]
示例 5:
**输入:** intervals = [[1,5]], newInterval = [2,7]
**输出:** [[1,7]]
提示:
0 <= intervals.length <= 104intervals[i].length == 20 <= intervals[i][0] <= intervals[i][1] <= 105intervals 根据 intervals[i][0] 按 升序 排列newInterval.length == 20 <= newInterval[0] <= newInterval[1] <= 105
前言
对于区间 $S_1 = [l_1, r_1]$ 和 $S_2 = [l_2, r_2]$,如果它们之间没有重叠(没有交集),说明要么 $S_1$ 在 $S_2$ 的左侧,此时有 $r_1 < l_2$;要么 $S_1$ 在 $S_2$ 的右侧,此时有 $l_1 > r_2$。
如果 $r_1 < l_2$ 和 $l_1 > r_2$ 二者均不满足,说明 $S_1$ 和 $S_2$ 必定有交集,它们的交集即为
$$
[\max(l_1, l_2), \min(r_1, r_2)]
$$
并集即为
$$
[\min(l_1, l_2), \max(r_1, r_2)]
$$
方法一:模拟
思路与算法
在给定的区间集合 $\mathcal{X}$ 互不重叠的前提下,当我们需要插入一个新的区间 $S = [\textit{left}, \textit{right}]$ 时,我们只需要:
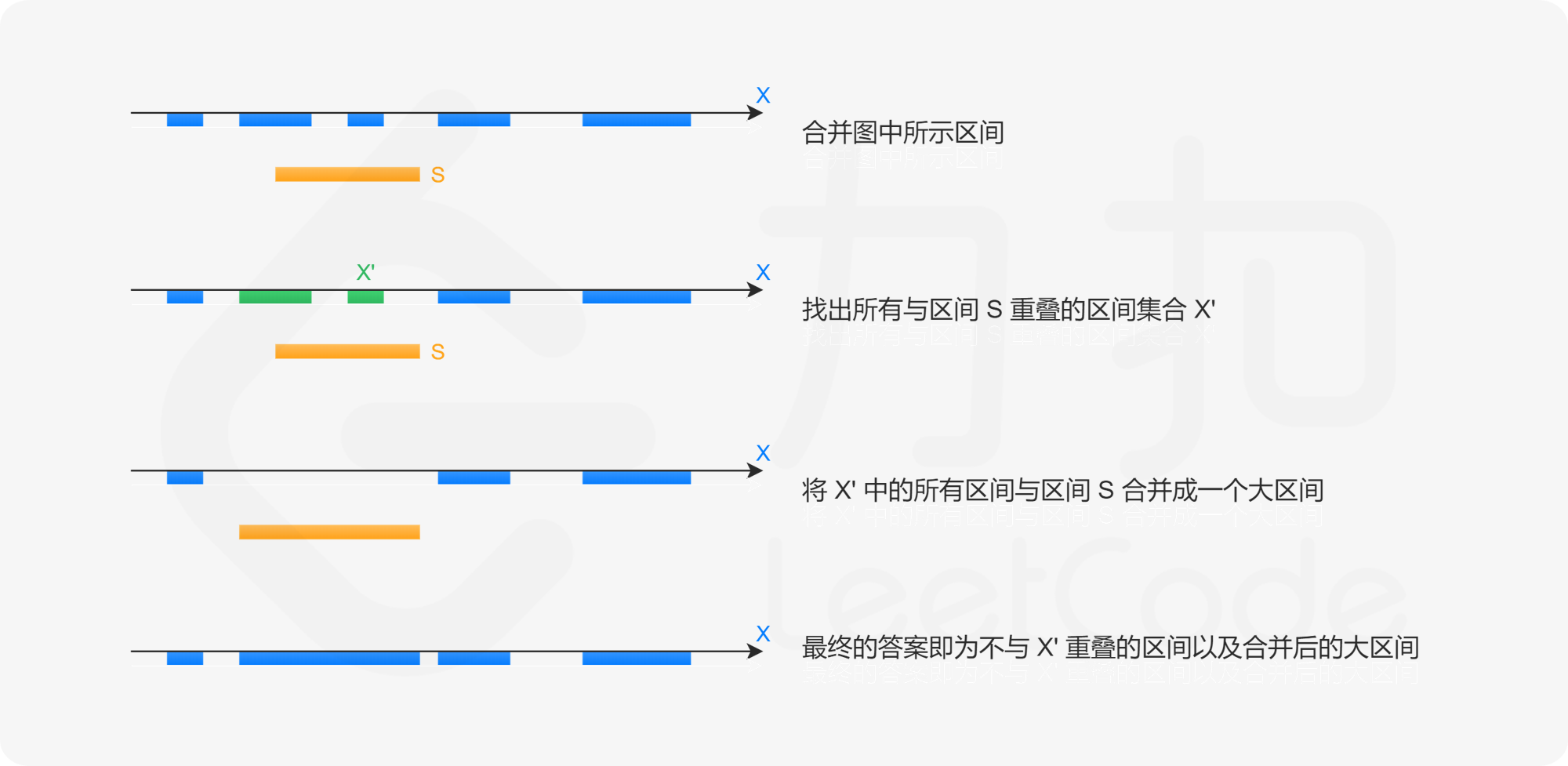
- 找出所有与区间 $S$ 重叠的区间集合 $\mathcal{X}’$;
- 将 $\mathcal{X}’$ 中的所有区间连带上区间 $S$ 合并成一个大区间;
- 最终的答案即为不与 $\mathcal{X}’$ 重叠的区间以及合并后的大区间。

这样做的正确性在于,给定的区间集合中任意两个区间都是没有交集的,因此所有需要合并的区间,就是所有与区间 $S$ 重叠的区间。
并且,在给定的区间集合已经按照左端点排序的前提下,所有与区间 $S$ 重叠的区间在数组 $\textit{intervals}$ 中下标范围是连续的,因此我们可以对所有的区间进行一次遍历,就可以找到这个连续的下标范围。
当我们遍历到区间 $[l_i, r_i]$ 时:
如果 $r_i < \textit{left}$,说明 $[l_i, r_i]$ 与 $S$ 不重叠并且在其左侧,我们可以直接将 $[l_i, r_i]$ 加入答案;
如果 $l_i > \textit{right}$,说明 $[l_i, r_i]$ 与 $S$ 不重叠并且在其右侧,我们可以直接将 $[l_i, r_i]$ 加入答案;
如果上面两种情况均不满足,说明 $[l_i, r_i]$ 与 $S$ 重叠,我们无需将 $[l_i, r_i]$ 加入答案。此时,我们需要将 $S$ 与 $[l_i, r_i]$ 合并,即将 $S$ 更新为其与 $[l_i, r_i]$ 的并集。
那么我们应当在什么时候将区间 $S$ 加入答案呢?由于我们需要保证答案也是按照左端点排序的,因此当我们遇到第一个 满足 $l_i > \textit{right}$ 的区间时,说明以后遍历到的区间不会与 $S$ 重叠,并且它们左端点一定会大于 $S$ 的左端点。此时我们就可以将 $S$ 加入答案。特别地,如果不存在这样的区间,我们需要在遍历结束后,将 $S$ 加入答案。
代码
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| class Solution {
public:
vector<vector<int>> insert(vector<vector<int>>& intervals, vector<int>& newInterval) {
int left = newInterval[0];
int right = newInterval[1];
bool placed = false;
vector<vector<int>> ans;
for (const auto& interval: intervals) {
if (interval[0] > right) {
if (!placed) {
ans.push_back({left, right});
placed = true;
}
ans.push_back(interval);
}
else if (interval[1] < left) {
ans.push_back(interval);
}
else {
left = min(left, interval[0]);
right = max(right, interval[1]);
}
}
if (!placed) {
ans.push_back({left, right});
}
return ans;
}
};
|
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| class Solution {
public int[][] insert(int[][] intervals, int[] newInterval) {
int left = newInterval[0];
int right = newInterval[1];
boolean placed = false;
List<int[]> ansList = new ArrayList<int[]>();
for (int[] interval : intervals) {
if (interval[0] > right) {
if (!placed) {
ansList.add(new int[]{left, right});
placed = true;
}
ansList.add(interval);
} else if (interval[1] < left) {
ansList.add(interval);
} else {
left = Math.min(left, interval[0]);
right = Math.max(right, interval[1]);
}
}
if (!placed) {
ansList.add(new int[]{left, right});
}
int[][] ans = new int[ansList.size()][2];
for (int i = 0; i < ansList.size(); ++i) {
ans[i] = ansList.get(i);
}
return ans;
}
}
|
[sol1-Python3]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class Solution:
def insert(self, intervals: List[List[int]], newInterval: List[int]) -> List[List[int]]:
left, right = newInterval
placed = False
ans = list()
for li, ri in intervals:
if li > right:
if not placed:
ans.append([left, right])
placed = True
ans.append([li, ri])
elif ri < left:
ans.append([li, ri])
else:
left = min(left, li)
right = max(right, ri)
if not placed:
ans.append([left, right])
return ans
|
[sol1-Golang]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| func insert(intervals [][]int, newInterval []int) (ans [][]int) {
left, right := newInterval[0], newInterval[1]
merged := false
for _, interval := range intervals {
if interval[0] > right {
if !merged {
ans = append(ans, []int{left, right})
merged = true
}
ans = append(ans, interval)
} else if interval[1] < left {
ans = append(ans, interval)
} else {
left = min(left, interval[0])
right = max(right, interval[1])
}
}
if !merged {
ans = append(ans, []int{left, right})
}
return
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
|
[sol1-C]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| int** insert(int** intervals, int intervalsSize, int* intervalsColSize, int* newInterval, int newIntervalSize, int* returnSize, int** returnColumnSizes) {
*returnSize = 0;
int left = newInterval[0];
int right = newInterval[1];
bool placed = false;
int** ans = malloc(sizeof(int*) * (intervalsSize + 1));
*returnColumnSizes = malloc(sizeof(int*) * (intervalsSize + 1));
for (int i = 0; i < intervalsSize; ++i) {
int* interval = intervals[i];
if (interval[0] > right) {
if (!placed) {
int* tmp = malloc(sizeof(int) * 2);
tmp[0] = left, tmp[1] = right;
(*returnColumnSizes)[*returnSize] = 2;
ans[(*returnSize)++] = tmp;
placed = true;
}
int* tmp = malloc(sizeof(int) * 2);
memcpy(tmp, interval, sizeof(int) * 2);
(*returnColumnSizes)[*returnSize] = 2;
ans[(*returnSize)++] = tmp;
} else if (interval[1] < left) {
int* tmp = malloc(sizeof(int) * 2);
memcpy(tmp, interval, sizeof(int) * 2);
(*returnColumnSizes)[*returnSize] = 2;
ans[(*returnSize)++] = tmp;
} else {
left = fmin(left, interval[0]);
right = fmax(right, interval[1]);
}
}
if (!placed) {
int* tmp = malloc(sizeof(int) * 2);
tmp[0] = left, tmp[1] = right;
(*returnColumnSizes)[*returnSize] = 2;
ans[(*returnSize)++] = tmp;
}
return ans;
}
|
复杂度分析