0064-最小路径和
给定一个包含非负整数的 _m_ x _n_ 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明: 每次只能向下或者向右移动一步。
示例 1:

**输入:** grid = [[1,3,1],[1,5,1],[4,2,1]]
**输出:** 7
**解释:** 因为路径 1→3→1→1→1 的总和最小。
示例 2:
**输入:** grid = [[1,2,3],[4,5,6]]
**输出:** 12
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 2000 <= grid[i][j] <= 200
解题思路:
此题是典型的动态规划题目。
状态定义:
- 设 $dp$ 为大小 $m \times n$ 矩阵,其中 $dp[i][j]$ 的值代表直到走到 $(i,j)$ 的最小路径和。
转移方程:
题目要求,只能向右或向下走,换句话说,当前单元格 $(i,j)$ 只能从左方单元格 $(i-1,j)$ 或上方单元格 $(i,j-1)$ 走到,因此只需要考虑矩阵左边界和上边界。
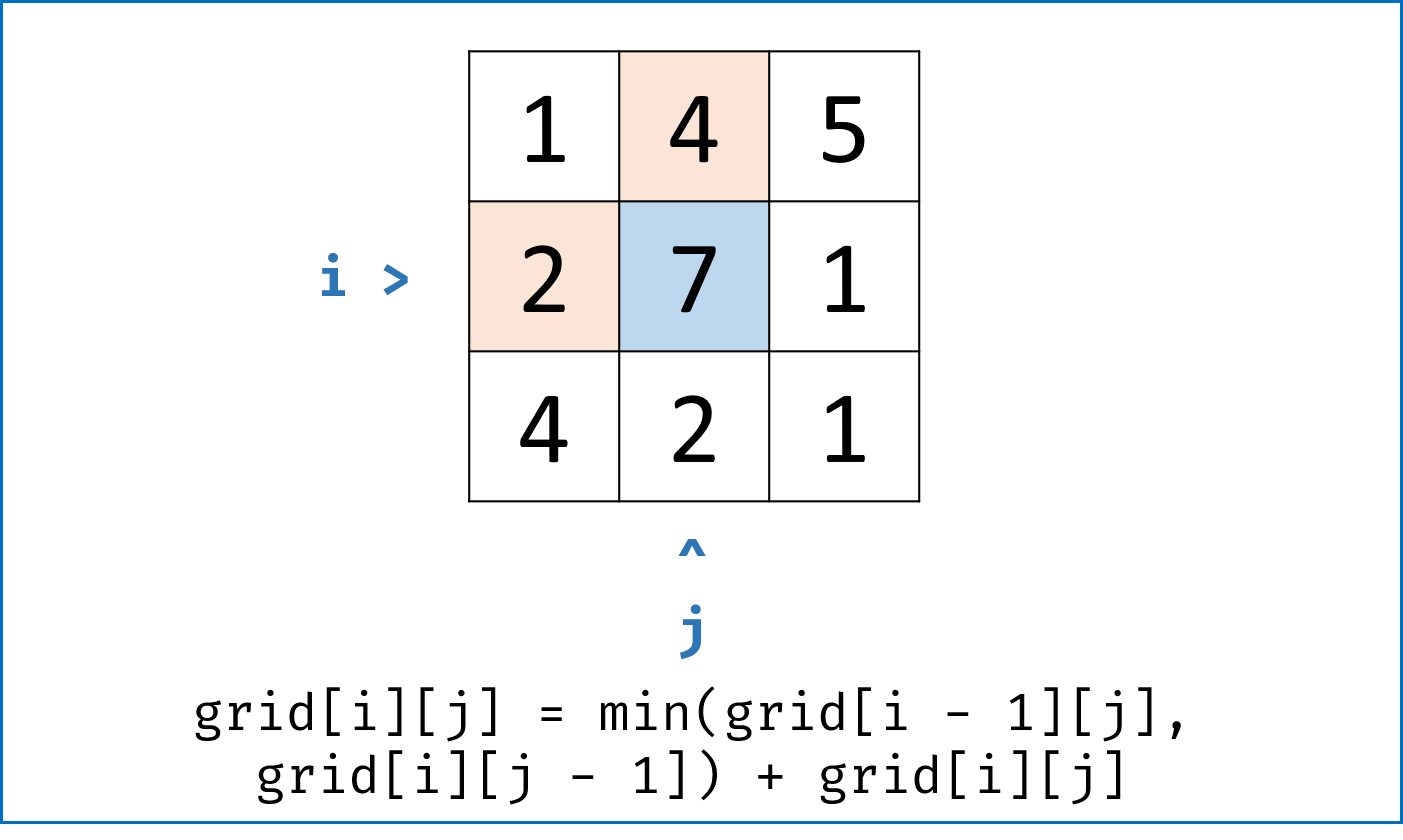
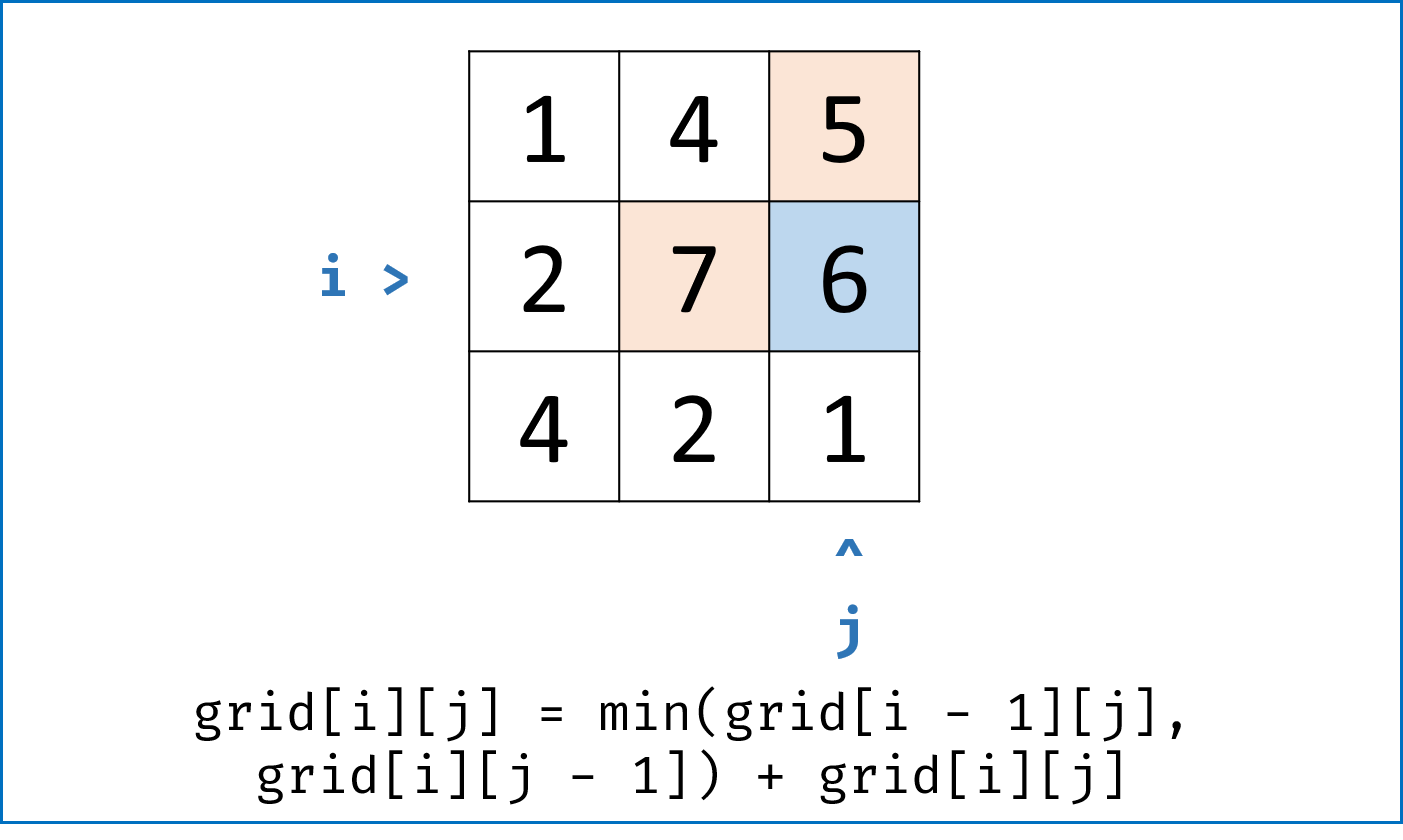
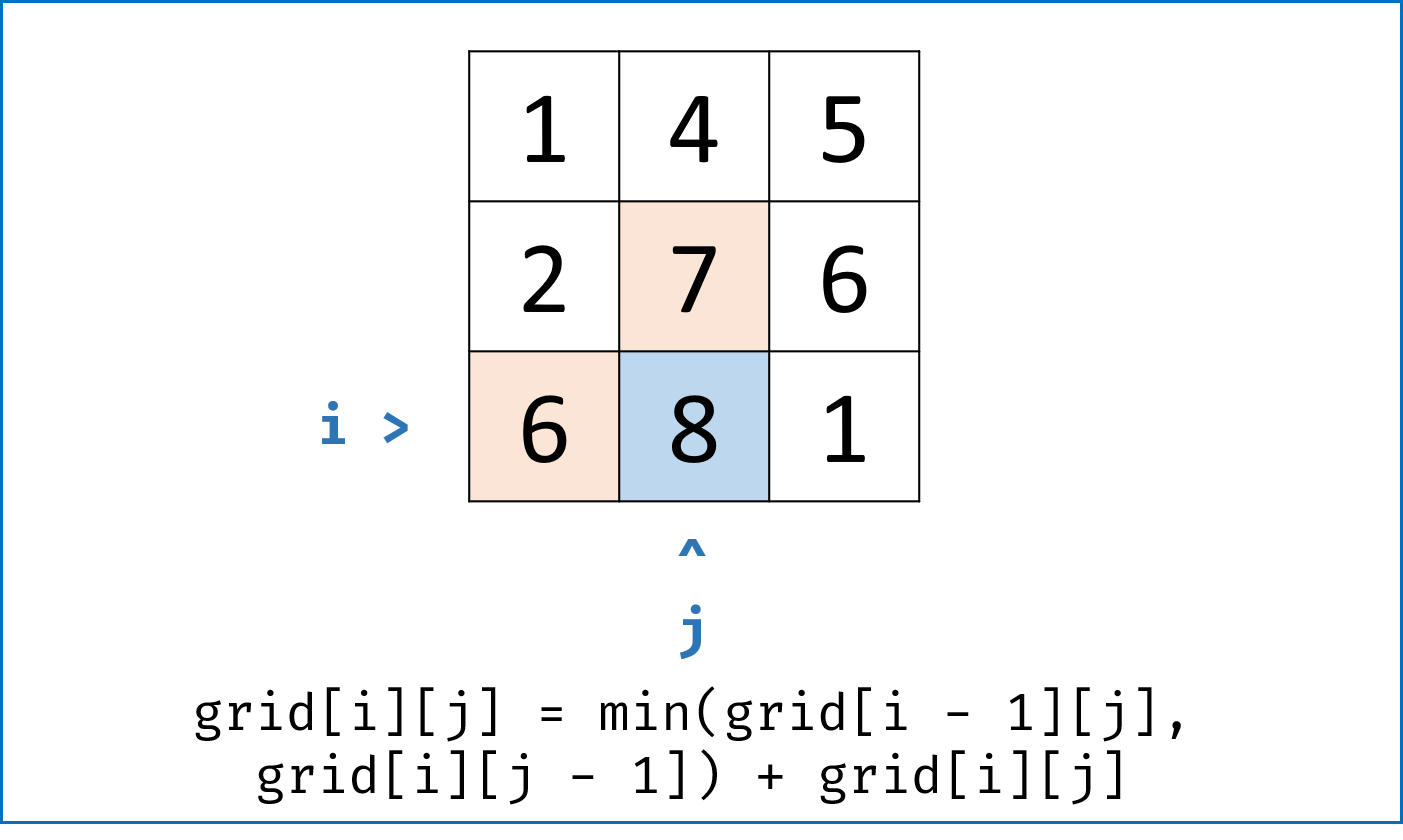
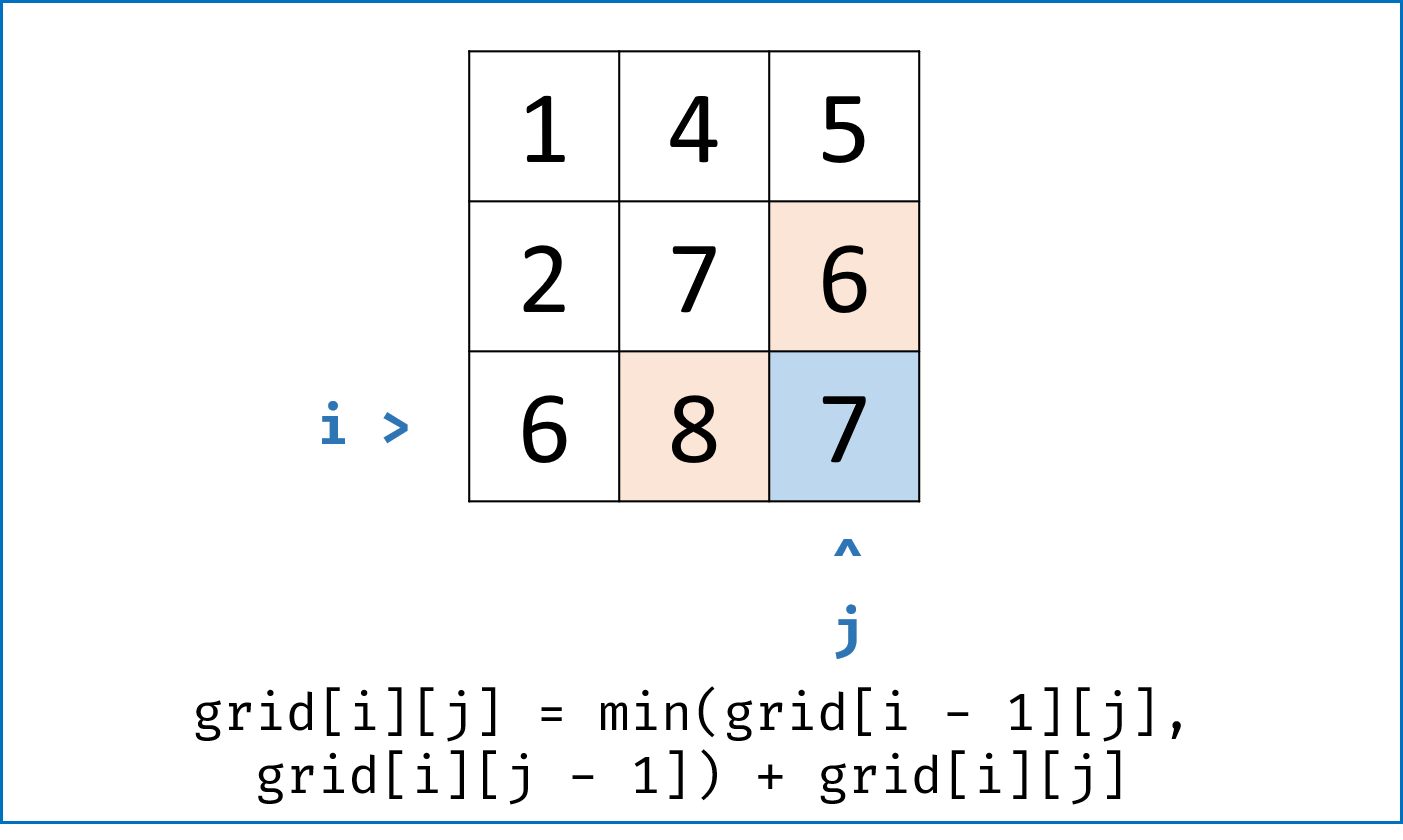
- 走到当前单元格 $(i,j)$ 的最小路径和 $=$ “从左方单元格 $(i-1,j)$ 与 从上方单元格 $(i,j-1)$ 走来的 两个最小路径和中较小的 ” $+$ 当前单元格值 $grid[i][j]$ 。具体分为以下 $4$ 种情况:
- 当左边和上边都不是矩阵边界时: 即当$i \not= 0$, $j \not= 0$时,$dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]$ ;
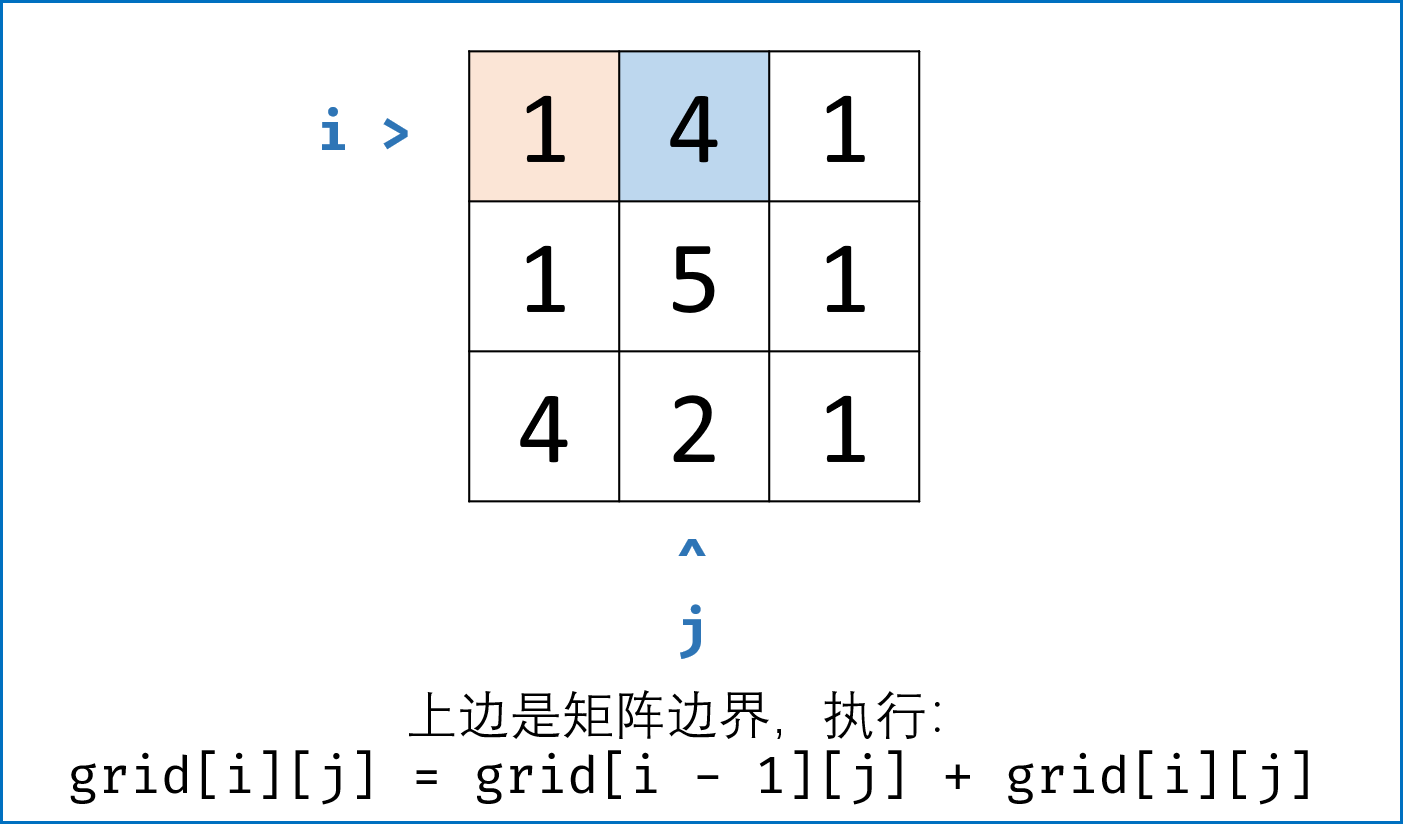
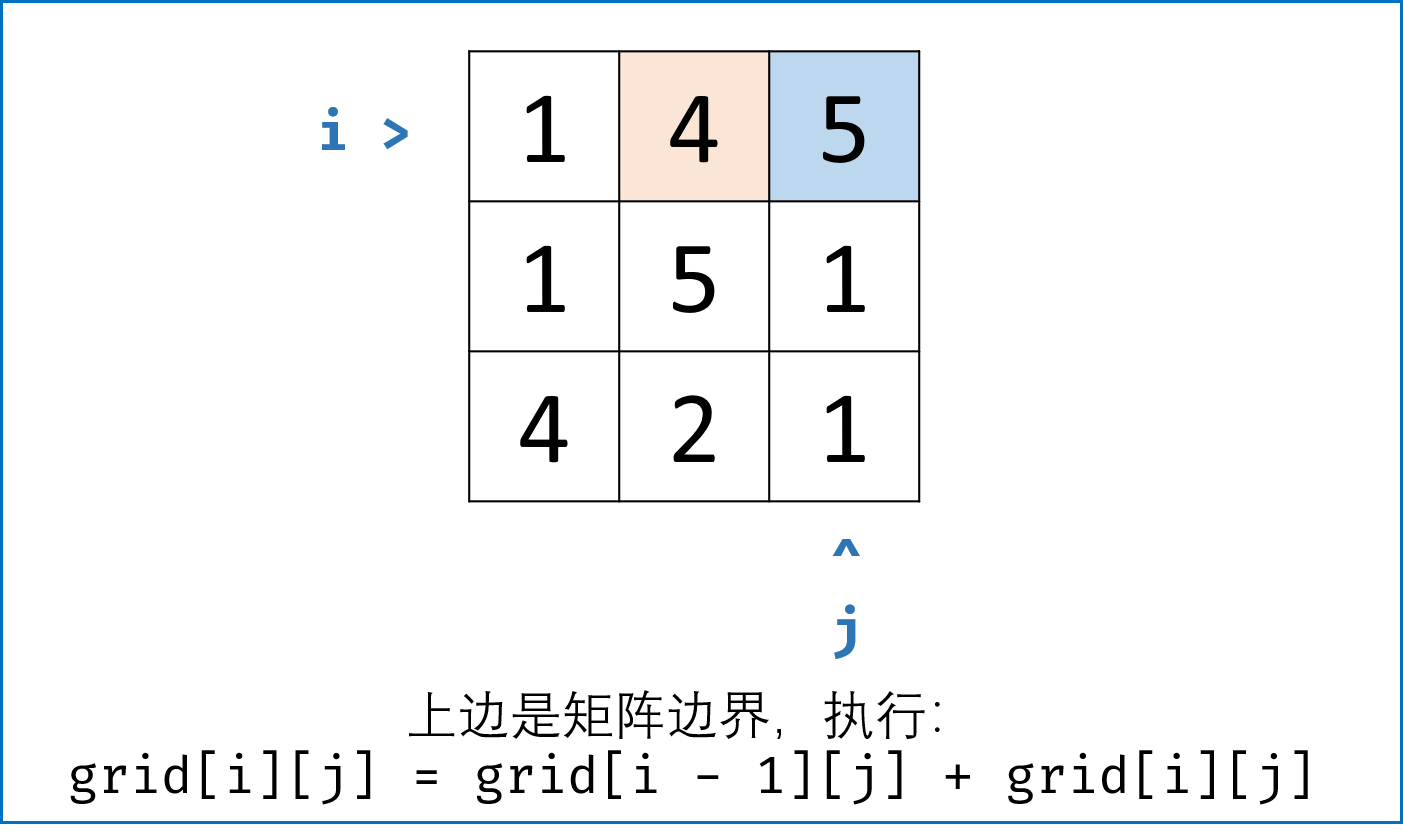
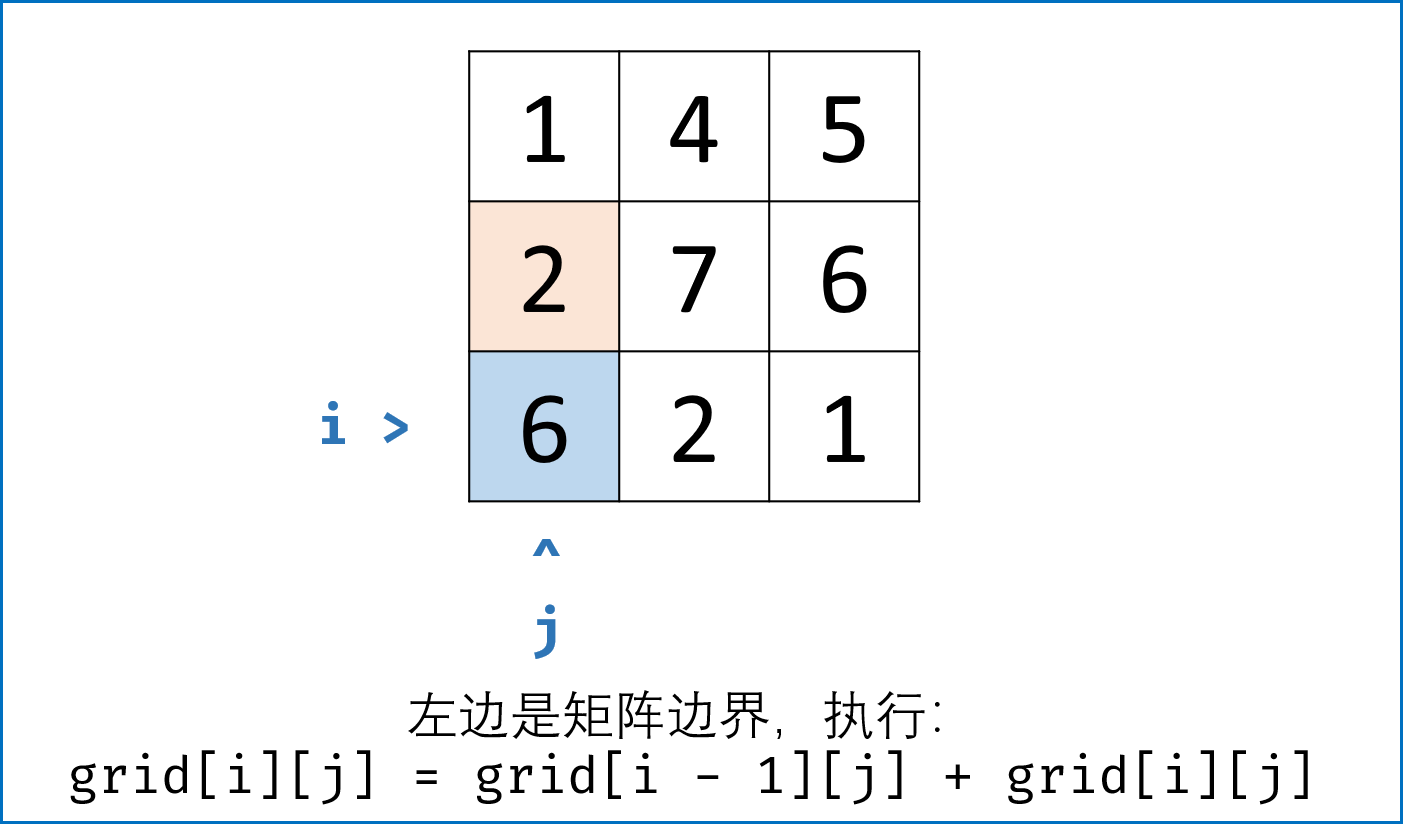
- 当只有左边是矩阵边界时: 只能从上面来,即当$i = 0, j \not= 0$时, $dp[i][j] = dp[i][j - 1] + grid[i][j]$ ;
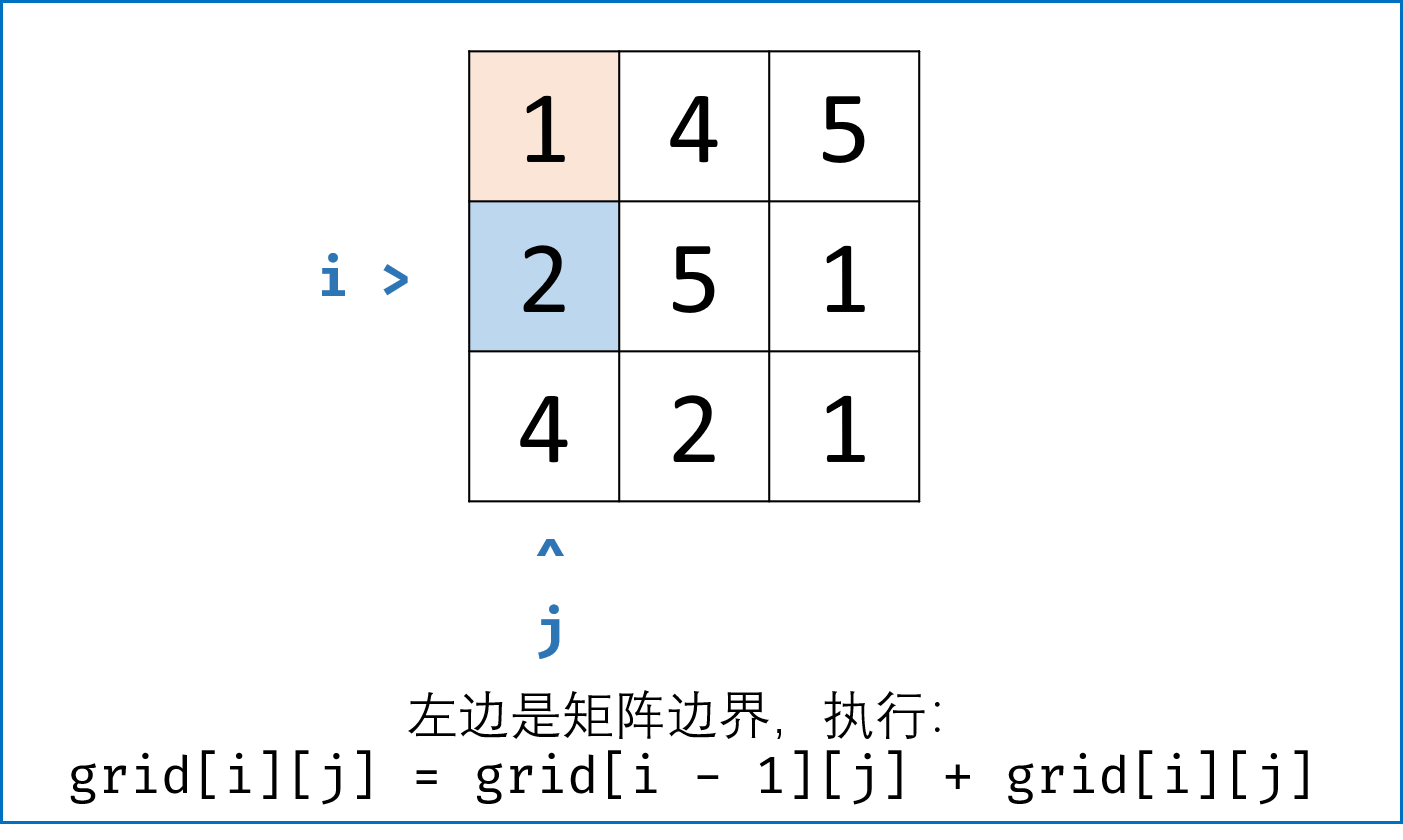
- 当只有上边是矩阵边界时: 只能从左面来,即当$i \not= 0, j = 0$时, $dp[i][j] = dp[i - 1][j] + grid[i][j]$ ;
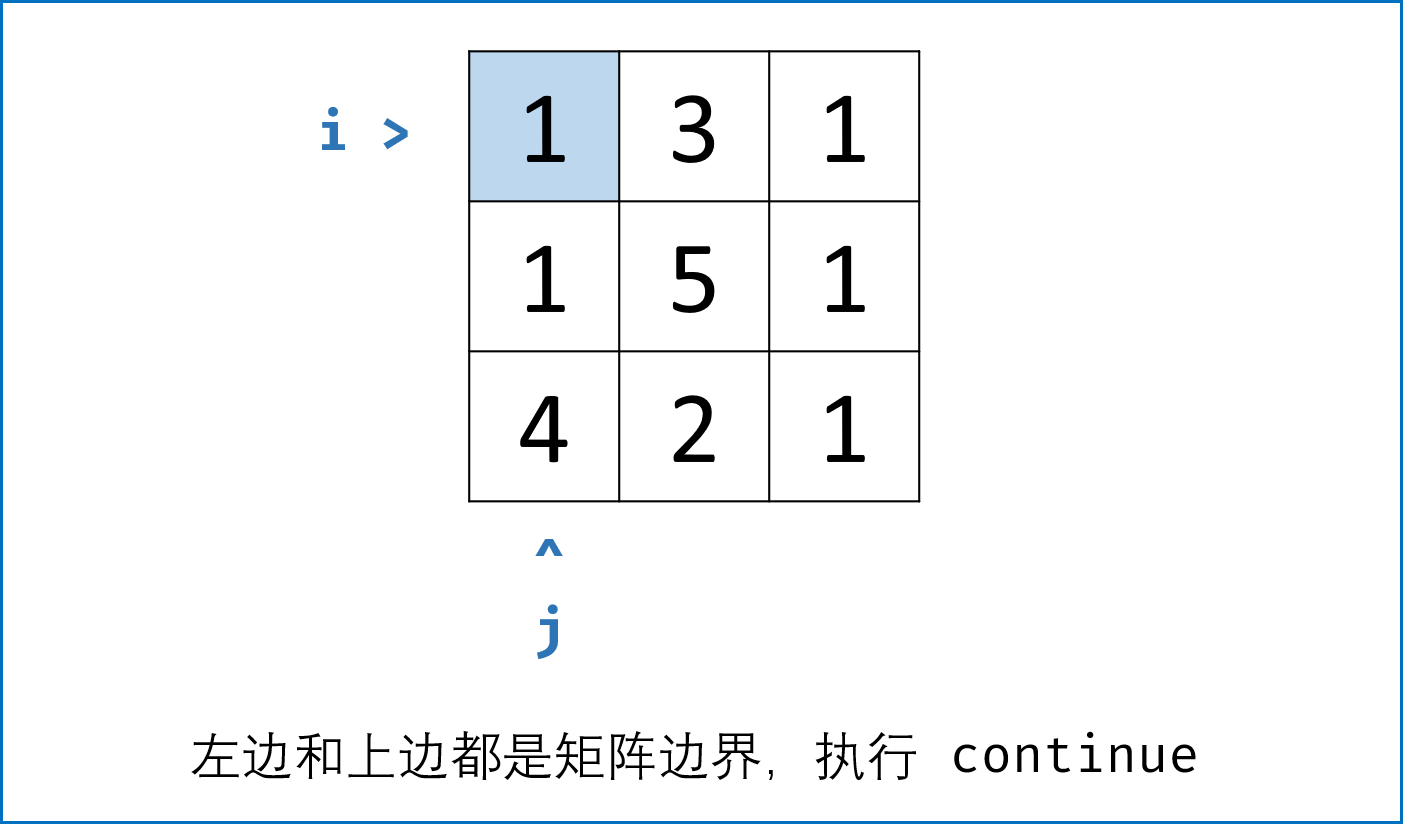
- 当左边和上边都是矩阵边界时: 即当$i = 0, j = 0$时,其实就是起点, $dp[i][j] = grid[i][j]$;
初始状态:
- $dp$ 初始化即可,不需要修改初始 $0$ 值。
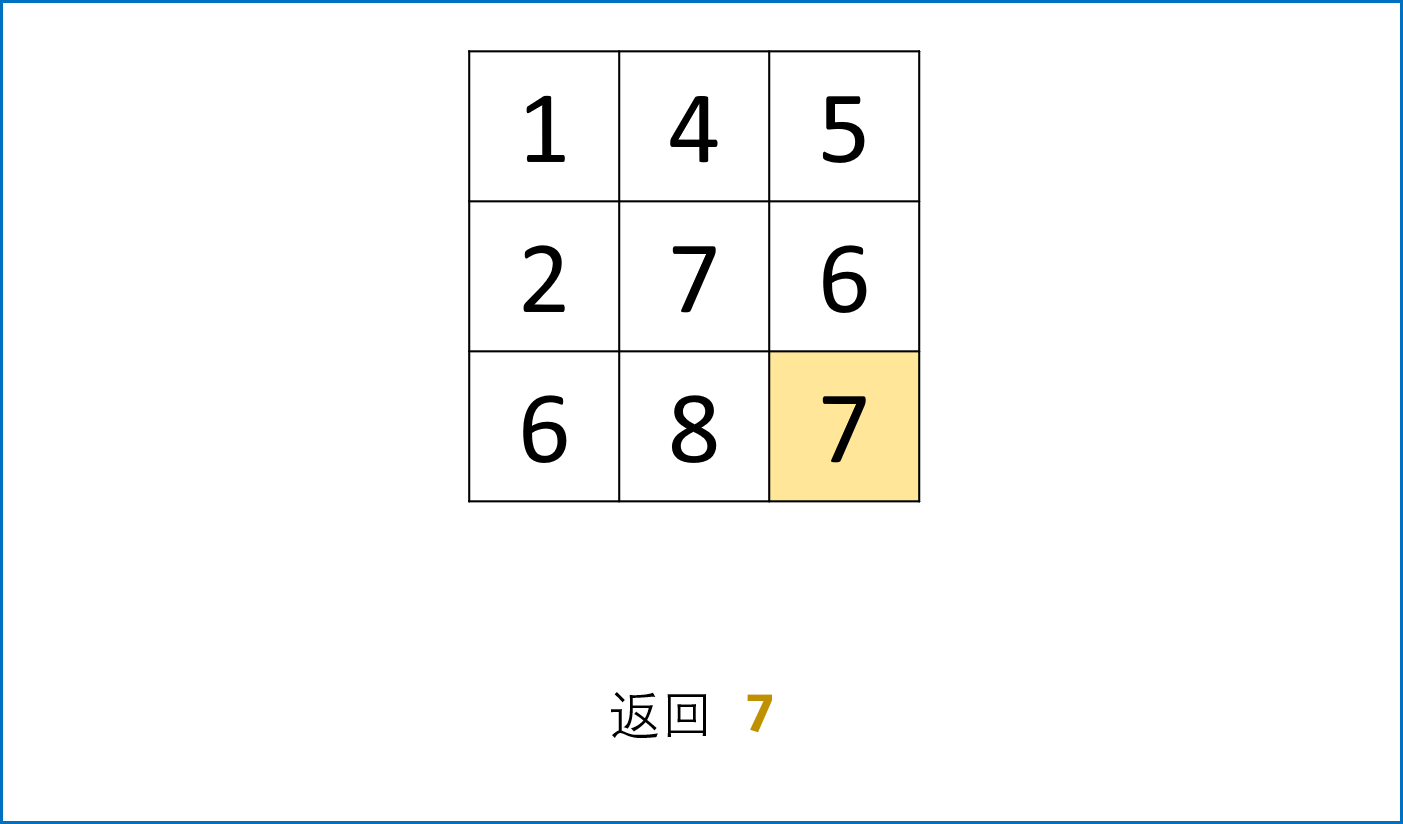
返回值:
- 返回 $dp$ 矩阵右下角值,即走到终点的最小路径和。
其实我们完全不需要建立 $dp$ 矩阵浪费额外空间,直接遍历 $grid[i][j]$ 修改即可。这是因为:grid[i][j] = min(grid[i - 1][j], grid[i][j - 1]) + grid[i][j] ;原 $grid$ 矩阵元素中被覆盖为 $dp$ 元素后(都处于当前遍历点的左上方),不会再被使用到。
复杂度分析:
- 时间复杂度 $O(M \times N)$ : 遍历整个 $grid$ 矩阵元素。
- 空间复杂度 $O(1)$ : 直接修改原矩阵,不使用额外空间。
< ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>
代码:
1 | class Solution: |
1 | class Solution { |
本学习计划配有代码仓,内含测试样例与数据结构封装,便于本地调试。可前往我的个人主页 获取。
Comments
