0069-x 的平方根

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 10:41:36 2023-09-13 10:41:36 Updated    

给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。

注意： 不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

示例 1：

**输入：** x = 4
**输出：** 2

示例 2：

**输入：** x = 8
**输出：** 2
**解释：** 8 的算术平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去。

提示：

  • 0 <= x <= 231 - 1

📺 视频题解

69 x的平方根 仲耀晖.mp4

📖 文字题解

前言

本题是一道常见的面试题，面试官一般会要求面试者在不使用 $\sqrt{x}$ 函数的情况下，得到 $x$ 的平方根的整数部分。一般的思路会有以下几种：

  • 通过其它的数学函数代替平方根函数得到精确结果，取整数部分作为答案；

  • 通过数学方法得到近似结果，直接作为答案。

方法一：袖珍计算器算法

「袖珍计算器算法」是一种用指数函数 $\exp$ 和对数函数 $\ln$ 代替平方根函数的方法。我们通过有限的可以使用的数学函数，得到我们想要计算的结果。

我们将 $\sqrt{x}$ 写成幂的形式 $x^{1/2}$，再使用自然对数 $e$ 进行换底，即可得到

$$
\sqrt{x} = x^{1/2} = (e ^ {\ln x})^{1/2} = e^{\frac{1}{2} \ln x}
$$

这样我们就可以得到 $\sqrt{x}$ 的值了。

注意： 由于计算机无法存储浮点数的精确值（浮点数的存储方法可以参考 IEEE 754 ，这里不再赘述），而指数函数和对数函数的参数和返回值均为浮点数，因此运算过程中会存在误差。例如当 $x = 2147395600$ 时，$e^{\frac{1}{2} \ln x}$ 的计算结果与正确值 $46340$ 相差 $10^{-11}$，这样在对结果取整数部分时，会得到 $46339$ 这个错误的结果。

因此在得到结果的整数部分 $\textit{ans}$ 后，我们应当找出 $\textit{ans}$ 与 $\textit{ans} + 1$ 中哪一个是真正的答案。

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    int mySqrt(int x) {
        if (x == 0) {
            return 0;
        }
        int ans = exp(0.5 * log(x));
        return ((long long)(ans + 1) * (ans + 1) <= x ? ans + 1 : ans);
    }
};
[sol1-Java]
1
2
3
4
5
6
7
8
9
class Solution {
    public int mySqrt(int x) {
        if (x == 0) {
            return 0;
        }
        int ans = (int) Math.exp(0.5 * Math.log(x));
        return (long) (ans + 1) * (ans + 1) <= x ? ans + 1 : ans;
    }
}
[sol1-Python3]
1
2
3
4
5
6
class Solution:
    def mySqrt(self, x: int) -> int:
        if x == 0:
            return 0
        ans = int(math.exp(0.5 * math.log(x)))
        return ans + 1 if (ans + 1) ** 2 <= x else ans
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
func mySqrt(x int) int {
    if x == 0 {
        return 0
    }
    ans := int(math.Exp(0.5 * math.Log(float64(x))))
    if (ans + 1) * (ans + 1) <= x {
        return ans + 1
    }
    return ans
}

复杂度分析

  • 时间复杂度：$O(1)$，由于内置的 exp 函数与 log 函数一般都很快，我们在这里将其复杂度视为 $O(1)$。

  • 空间复杂度：$O(1)$。

方法二：二分查找

由于 $x$ 平方根的整数部分 $\textit{ans}$ 是满足 $k^2 \leq x$ 的最大 $k$ 值，因此我们可以对 $k$ 进行二分查找，从而得到答案。

二分查找的下界为 $0$，上界可以粗略地设定为 $x$。在二分查找的每一步中，我们只需要比较中间元素 $\textit{mid}$ 的平方与 $x$ 的大小关系，并通过比较的结果调整上下界的范围。由于我们所有的运算都是整数运算，不会存在误差，因此在得到最终的答案 $\textit{ans}$ 后，也就不需要再去尝试 $\textit{ans} + 1$ 了。

[sol2-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int mySqrt(int x) {
        int l = 0, r = x, ans = -1;
        while (l <= r) {
            int mid = l + (r - l) / 2;
            if ((long long)mid * mid <= x) {
                ans = mid;
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }
        return ans;
    }
};
[sol2-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int mySqrt(int x) {
        int l = 0, r = x, ans = -1;
        while (l <= r) {
            int mid = l + (r - l) / 2;
            if ((long) mid * mid <= x) {
                ans = mid;
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }
        return ans;
    }
}
[sol2-Python3]
1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def mySqrt(self, x: int) -> int:
        l, r, ans = 0, x, -1
        while l <= r:
            mid = (l + r) // 2
            if mid * mid <= x:
                ans = mid
                l = mid + 1
            else:
                r = mid - 1
        return ans
[sol2-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
func mySqrt(x int) int {
    l, r := 0, x
    ans := -1
    for l <= r {
        mid := l + (r - l) / 2
        if mid * mid <= x {
            ans = mid
            l = mid + 1
        } else {
            r = mid - 1
        }
    }
    return ans
}

复杂度分析

  • 时间复杂度：$O(\log x)$，即为二分查找需要的次数。

  • 空间复杂度：$O(1)$。

方法三：牛顿迭代

思路

牛顿迭代法 是一种可以用来快速求解函数零点的方法。

为了叙述方便，我们用 $C$ 表示待求出平方根的那个整数。显然，$C$ 的平方根就是函数

$$
y = f(x) = x^2 - C
$$

的零点。

牛顿迭代法的本质是借助泰勒级数，从初始值开始快速向零点逼近。我们任取一个 $x_0$ 作为初始值，在每一步的迭代中，我们找到函数图像上的点 $(x_i, f(x_i))$，过该点作一条斜率为该点导数 $f’(x_i)$ 的直线，与横轴的交点记为 $x_{i+1}$。$x_{i+1}$ 相较于 $x_i$ 而言距离零点更近。在经过多次迭代后，我们就可以得到一个距离零点非常接近的交点。下图给出了从 $x_0$ 开始迭代两次，得到 $x_1$ 和 $x_2$ 的过程。

fig1

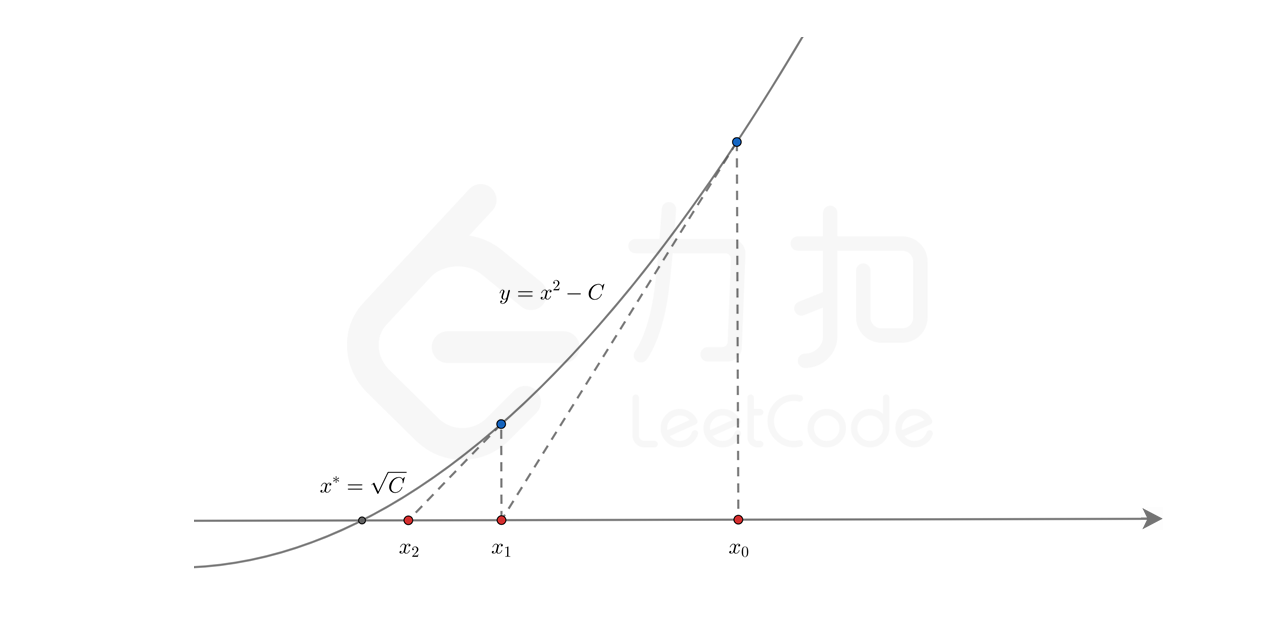
算法

我们选择 $x_0 = C$ 作为初始值。

在每一步迭代中，我们通过当前的交点 $x_i$，找到函数图像上的点 $(x_i, x_i^2 - C)$，作一条斜率为 $f’(x_i) = 2x_i$ 的直线，直线的方程为：

$$
\begin{aligned}
y_l &= 2x_i(x - x_i) + x_i^2 - C \
&= 2x_ix - (x_i^2 + C)
\end{aligned}
$$

与横轴的交点为方程 $2x_ix - (x_i^2 + C) = 0$ 的解，即为新的迭代结果 $x_{i+1}$：

$$
x_{i+1} = \frac{1}{2}\left(x_i + \frac{C}{x_i}\right)
$$

在进行 $k$ 次迭代后，$x_k$ 的值与真实的零点 $\sqrt{C}$ 足够接近，即可作为答案。

细节

  • 为什么选择 $x_0 = C$ 作为初始值？

    • 因为 $y = x^2 - C$ 有两个零点 $-\sqrt{C}$ 和 $\sqrt{C}$。如果我们取的初始值较小，可能会迭代到 $-\sqrt{C}$ 这个零点，而我们希望找到的是 $\sqrt{C}$ 这个零点。因此选择 $x_0 = C$ 作为初始值，每次迭代均有 $x_{i+1} < x_i$，零点 $\sqrt{C}$ 在其左侧，所以我们一定会迭代到这个零点。

  • 迭代到何时才算结束？

    • 每一次迭代后，我们都会距离零点更进一步，所以当相邻两次迭代得到的交点非常接近时，我们就可以断定，此时的结果已经足够我们得到答案了。一般来说，可以判断相邻两次迭代的结果的差值是否小于一个极小的非负数 $\epsilon$，其中 $\epsilon$ 一般可以取 $10^{-6}$ 或 $10^{-7}$。

  • 如何通过迭代得到的近似零点得出最终的答案？

    • 由于 $y = f(x)$ 在 $[\sqrt{C}, +\infty]$ 上是凸函数（convex function）且恒大于等于零，那么只要我们选取的初始值 $x_0$ 大于等于 $\sqrt{C}$，每次迭代得到的结果 $x_i$ 都会恒大于等于 $\sqrt{C}$。因此只要 $\epsilon$ 选择地足够小，最终的结果 $x_k$ 只会稍稍大于真正的零点 $\sqrt{C}$。在题目给出的 32 位整数范围内，不会出现下面的情况：

      真正的零点为 $n - 1/2\epsilon$，其中 $n$ 是一个正整数，而我们迭代得到的结果为 $n + 1/2\epsilon$。在对结果保留整数部分后得到 $n$，但正确的结果为 $n - 1$。

[sol3-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int mySqrt(int x) {
        if (x == 0) {
            return 0;
        }

        double C = x, x0 = x;
        while (true) {
            double xi = 0.5 * (x0 + C / x0);
            if (fabs(x0 - xi) < 1e-7) {
                break;
            }
            x0 = xi;
        }
        return int(x0);
    }
};
[sol3-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int mySqrt(int x) {
        if (x == 0) {
            return 0;
        }

        double C = x, x0 = x;
        while (true) {
            double xi = 0.5 * (x0 + C / x0);
            if (Math.abs(x0 - xi) < 1e-7) {
                break;
            }
            x0 = xi;
        }
        return (int) x0;
    }
}
[sol3-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
    def mySqrt(self, x: int) -> int:
        if x == 0:
            return 0
        
        C, x0 = float(x), float(x)
        while True:
            xi = 0.5 * (x0 + C / x0)
            if abs(x0 - xi) < 1e-7:
                break
            x0 = xi
        
        return int(x0)
[sol3-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
func mySqrt(x int) int {
    if x == 0 {
        return 0
    }
    C, x0 := float64(x), float64(x)
    for {
        xi := 0.5 * (x0 + C/x0)
        if math.Abs(x0 - xi) < 1e-7 {
            break
        }
        x0 = xi
    }
    return int(x0)
}

复杂度分析

  • 时间复杂度：$O(\log x)$，此方法是二次收敛的，相较于二分查找更快。

  • 空间复杂度：$O(1)$。

 Comments
On this page
0069-x 的平方根
  1. 📺 视频题解
  2. 📖 文字题解