给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
示例 1:
**输入:** word1 = "horse", word2 = "ros"
**输出:** 3
**解释:**
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
示例 2:
**输入:** word1 = "intention", word2 = "execution"
**输出:** 5
**解释:**
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')
提示:
0 <= word1.length, word2.length <= 500word1 和 word2 由小写英文字母组成
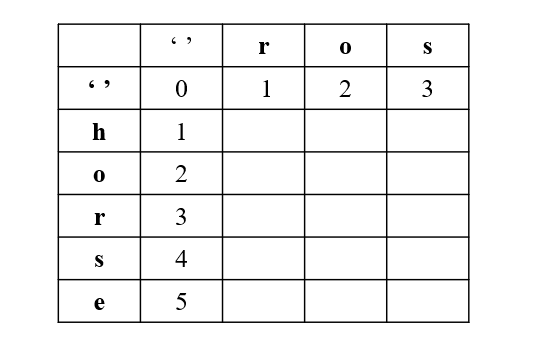
动态规划:
dp[i][j] 代表 word1 到 i 位置转换成 word2 到 j 位置需要最少步数
所以,
当 word1[i] == word2[j],dp[i][j] = dp[i-1][j-1];
当 word1[i] != word2[j],dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1
其中,dp[i-1][j-1] 表示替换操作,dp[i-1][j] 表示删除操作,dp[i][j-1] 表示插入操作。
注意,针对第一行,第一列要单独考虑,我们引入 '' 下图所示:
 {:width=”360”}
{:width=”360”}
{:align=center}
第一行,是 word1 为空变成 word2 最少步数,就是插入操作
第一列,是 word2 为空,需要的最少步数,就是删除操作
再附上自顶向下的方法,大家可以提供 Java 版吗?
代码:
自底向上
[1]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution:
def minDistance(self, word1: str, word2: str) -> int:
n1 = len(word1)
n2 = len(word2)
dp = [[0] * (n2 + 1) for _ in range(n1 + 1)]
for j in range(1, n2 + 1):
dp[0][j] = dp[0][j-1] + 1
for i in range(1, n1 + 1):
dp[i][0] = dp[i-1][0] + 1
for i in range(1, n1 + 1):
for j in range(1, n2 + 1):
if word1[i-1] == word2[j-1]:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = min(dp[i][j-1], dp[i-1][j], dp[i-1][j-1] ) + 1
return dp[-1][-1]
|
[1]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
public int minDistance(String word1, String word2) {
int n1 = word1.length();
int n2 = word2.length();
int[][] dp = new int[n1 + 1][n2 + 1];
for (int j = 1; j <= n2; j++) dp[0][j] = dp[0][j - 1] + 1;
for (int i = 1; i <= n1; i++) dp[i][0] = dp[i - 1][0] + 1;
for (int i = 1; i <= n1; i++) {
for (int j = 1; j <= n2; j++) {
if (word1.charAt(i - 1) == word2.charAt(j - 1)) dp[i][j] = dp[i - 1][j - 1];
else dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1], dp[i][j - 1]), dp[i - 1][j]) + 1;
}
}
return dp[n1][n2];
}
}
|
自顶向下
[2]1
2
3
4
5
6
7
8
9
10
11
12
13
| import functools
class Solution:
@functools.lru_cache(None)
def minDistance(self, word1: str, word2: str) -> int:
if not word1 or not word2:
return len(word1) + len(word2)
if word1[0] == word2[0]:
return self.minDistance(word1[1:], word2[1:])
else:
inserted = 1 + self.minDistance(word1, word2[1:])
deleted = 1 + self.minDistance(word1[1:], word2)
replace = 1 + self.minDistance(word1[1:], word2[1:])
return min(inserted, deleted, replace)
|
@shu-xie-fan 的建议,由于字符串切片是 $O(n)$,所以改成用了索引号。
[2]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| class Solution:
def minDistance(self, word1: str, word2: str) -> int:
import functools
@functools.lru_cache(None)
def helper(i, j):
if i == len(word1) or j == len(word2):
return len(word1) - i + len(word2) - j
if word1[i] == word2[j]:
return helper(i + 1, j + 1)
else:
inserted = helper(i, j + 1)
deleted = helper(i + 1, j)
replaced = helper(i + 1, j + 1)
return min(inserted, deleted, replaced) + 1
return helper(0, 0)
|
 {:width=”360”}
{:width=”360”}