给定一个包含红色、白色和蓝色、共 n __ 个元素的数组 nums ,原地
我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
必须在不使用库内置的 sort 函数的情况下解决这个问题。
示例 1:
**输入:** nums = [2,0,2,1,1,0]
**输出:** [0,0,1,1,2,2]
示例 2:
**输入:** nums = [2,0,1]
**输出:** [0,1,2]
提示:
n == nums.length1 <= n <= 300nums[i] 为 0、1 或 2
进阶:
📺 视频题解
📖 文字题解 前言 本题是经典的「荷兰国旗问题」,由计算机科学家 Edsger W. Dijkstra 首先提出。
根据题目中的提示,我们可以统计出数组中 $0, 1, 2$ 的个数,再根据它们的数量,重写整个数组。这种方法较为简单,也很容易想到,而本题解中会介绍两种基于指针进行交换的方法。
方法一:单指针 思路与算法
我们可以考虑对数组进行两次遍历。在第一次遍历中,我们将数组中所有的 $0$ 交换到数组的头部。在第二次遍历中,我们将数组中所有的 $1$ 交换到头部的 $0$ 之后。此时,所有的 $2$ 都出现在数组的尾部,这样我们就完成了排序。
具体地,我们使用一个指针 $\textit{ptr}$ 表示「头部」的范围,$\textit{ptr}$ 中存储了一个整数,表示数组 $\textit{nums}$ 从位置 $0$ 到位置 $\textit{ptr}-1$ 都属于「头部」。$\textit{ptr}$ 的初始值为 $0$,表示还没有数处于「头部」。
在第一次遍历中,我们从左向右遍历整个数组,如果找到了 $0$,那么就需要将 $0$ 与「头部」位置的元素进行交换,并将「头部」向后扩充一个位置。在遍历结束之后,所有的 $0$ 都被交换到「头部」的范围,并且「头部」只包含 $0$。
在第二次遍历中,我们从「头部」开始,从左向右遍历整个数组,如果找到了 $1$,那么就需要将 $1$ 与「头部」位置的元素进行交换,并将「头部」向后扩充一个位置。在遍历结束之后,所有的 $1$ 都被交换到「头部」的范围,并且都在 $0$ 之后,此时 $2$ 只出现在「头部」之外的位置,因此排序完成。
代码
[sol1-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution {public : void sortColors (vector<int >& nums) int n = nums.size (); int ptr = 0 ; for (int i = 0 ; i < n; ++i) { if (nums[i] == 0 ) { swap (nums[i], nums[ptr]); ++ptr; } } for (int i = ptr; i < n; ++i) { if (nums[i] == 1 ) { swap (nums[i], nums[ptr]); ++ptr; } } } };
[sol1-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution { public void sortColors (int [] nums) { int n = nums.length; int ptr = 0 ; for (int i = 0 ; i < n; ++i) { if (nums[i] == 0 ) { int temp = nums[i]; nums[i] = nums[ptr]; nums[ptr] = temp; ++ptr; } } for (int i = ptr; i < n; ++i) { if (nums[i] == 1 ) { int temp = nums[i]; nums[i] = nums[ptr]; nums[ptr] = temp; ++ptr; } } } }
[sol1-Python3] 1 2 3 4 5 6 7 8 9 10 11 12 class Solution : def sortColors (self, nums: List [int ] ) -> None : n = len (nums) ptr = 0 for i in range (n): if nums[i] == 0 : nums[i], nums[ptr] = nums[ptr], nums[i] ptr += 1 for i in range (ptr, n): if nums[i] == 1 : nums[i], nums[ptr] = nums[ptr], nums[i] ptr += 1
[sol1-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 func swapColors (colors []int , target int ) int ) { for i, c := range colors { if c == target { colors[i], colors[countTarget] = colors[countTarget], colors[i] countTarget++ } } return } func sortColors (nums []int ) count0 := swapColors(nums, 0 ) swapColors(nums[count0:], 1 ) }
[sol1-C] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 void swap (int *a, int *b) { int t = *a; *a = *b, *b = t; } void sortColors (int *nums, int numsSize) { int ptr = 0 ; for (int i = 0 ; i < numsSize; ++i) { if (nums[i] == 0 ) { swap(&nums[i], &nums[ptr]); ++ptr; } } for (int i = ptr; i < numsSize; ++i) { if (nums[i] == 1 ) { swap(&nums[i], &nums[ptr]); ++ptr; } } }
复杂度分析
方法二:双指针 思路与算法
方法一需要进行两次遍历,那么我们是否可以仅使用一次遍历呢?我们可以额外使用一个指针,即使用两个指针分别用来交换 $0$ 和 $1$。
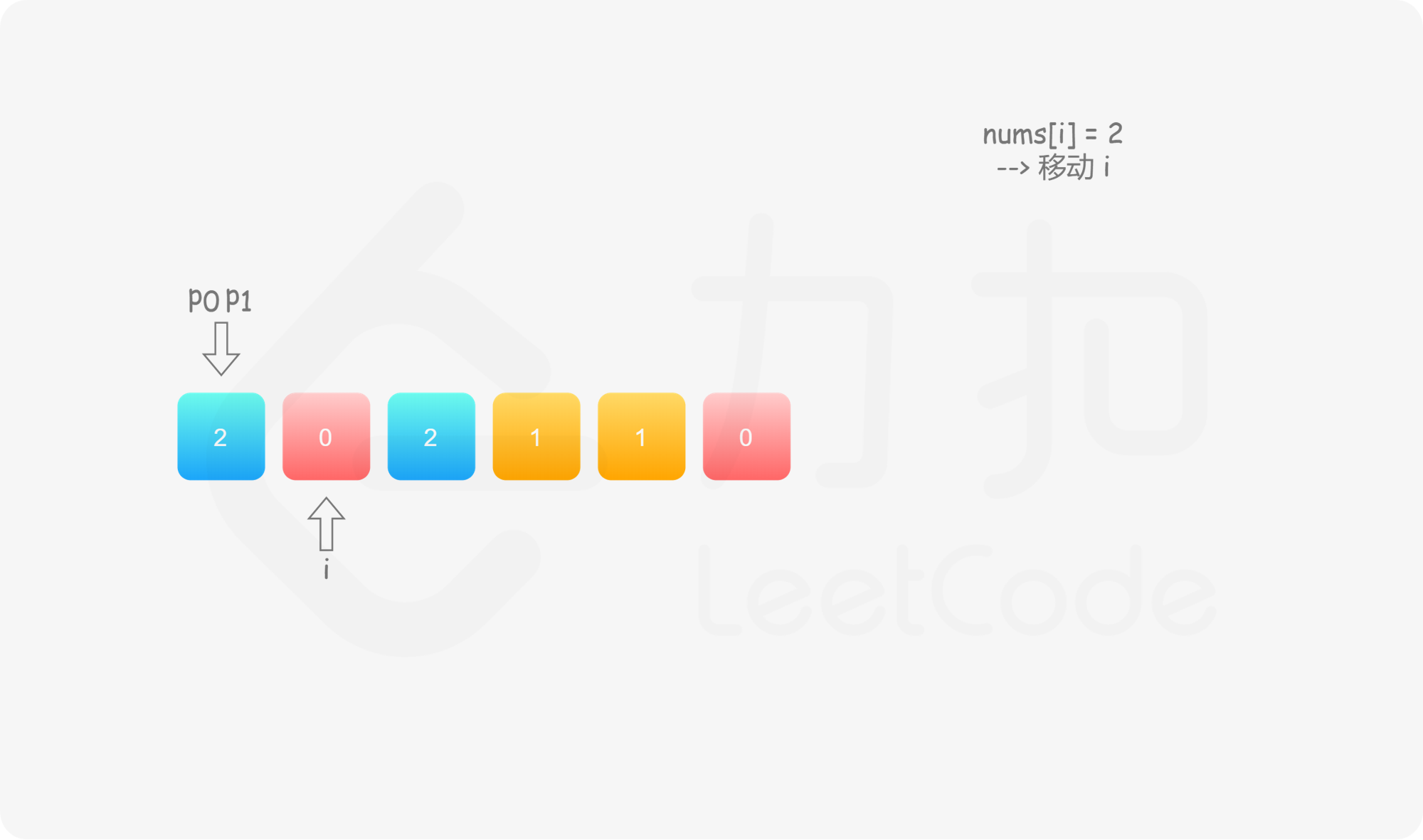
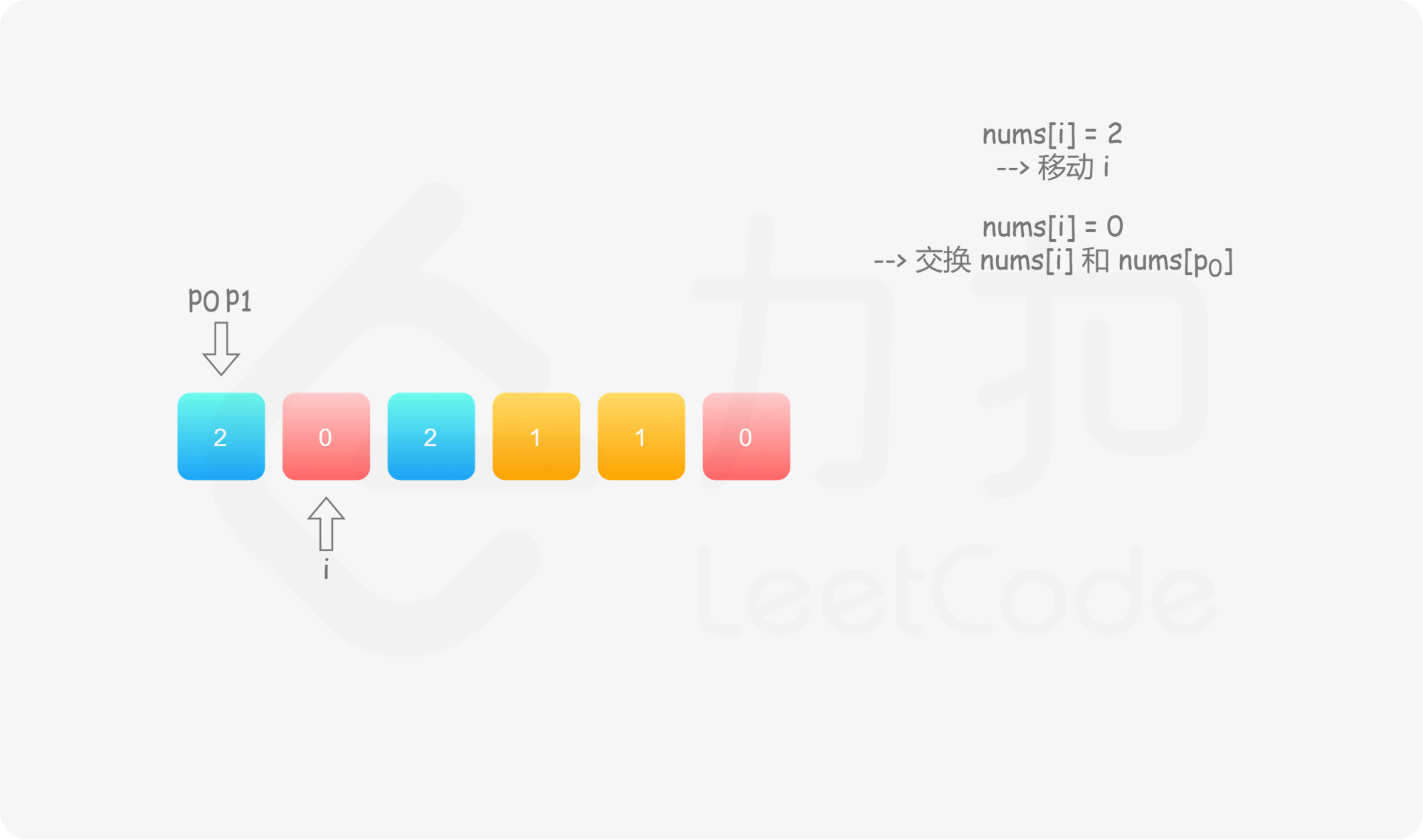
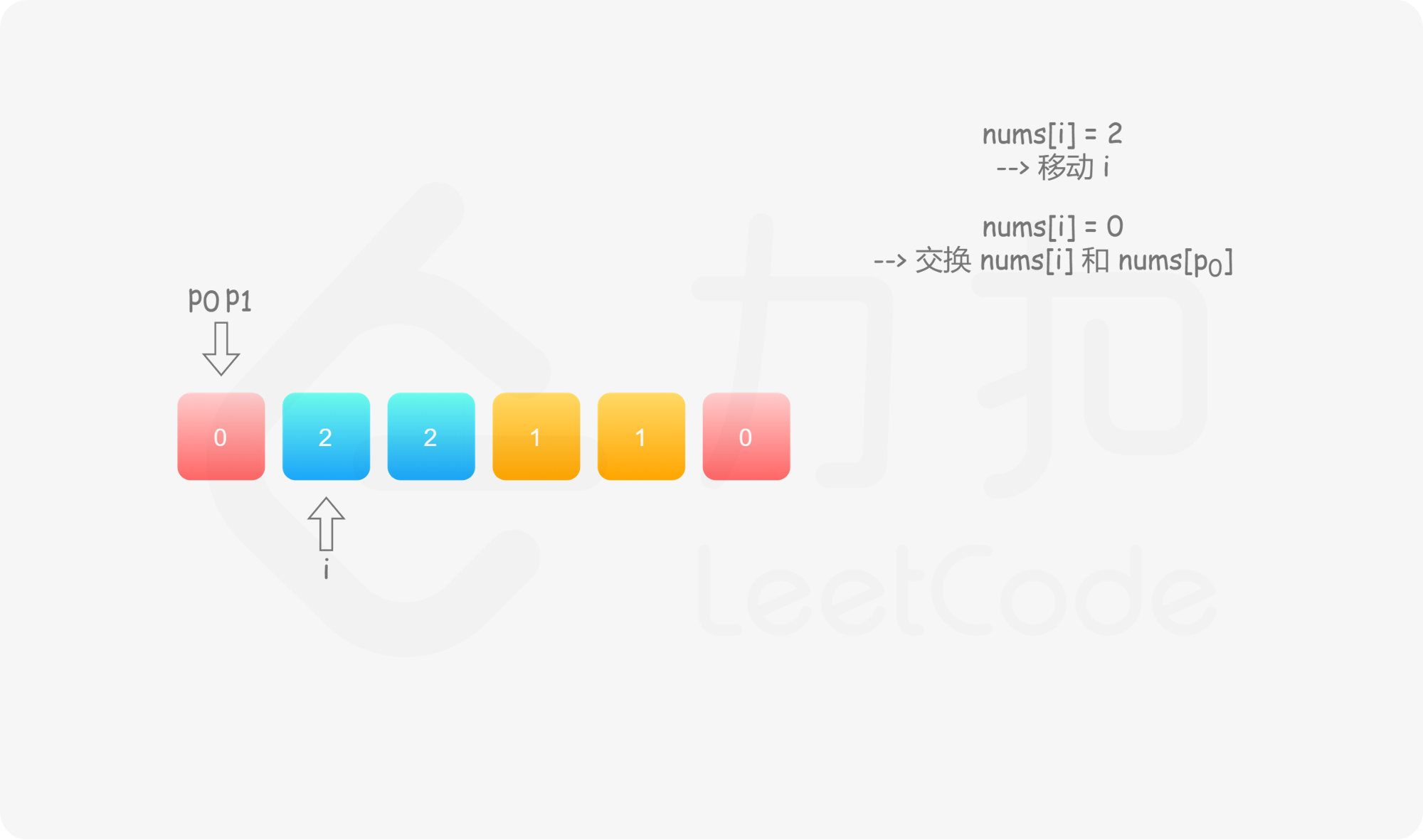
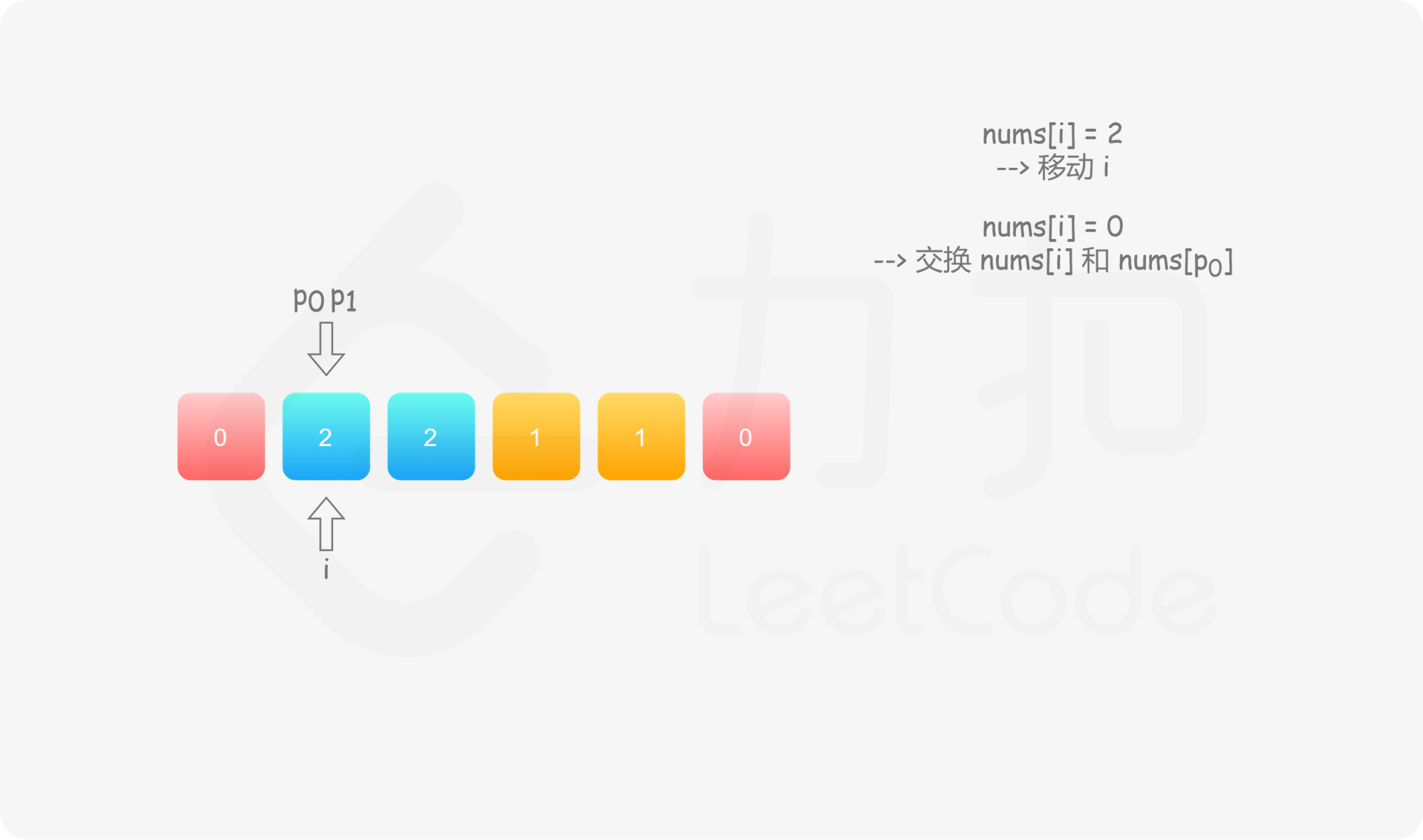
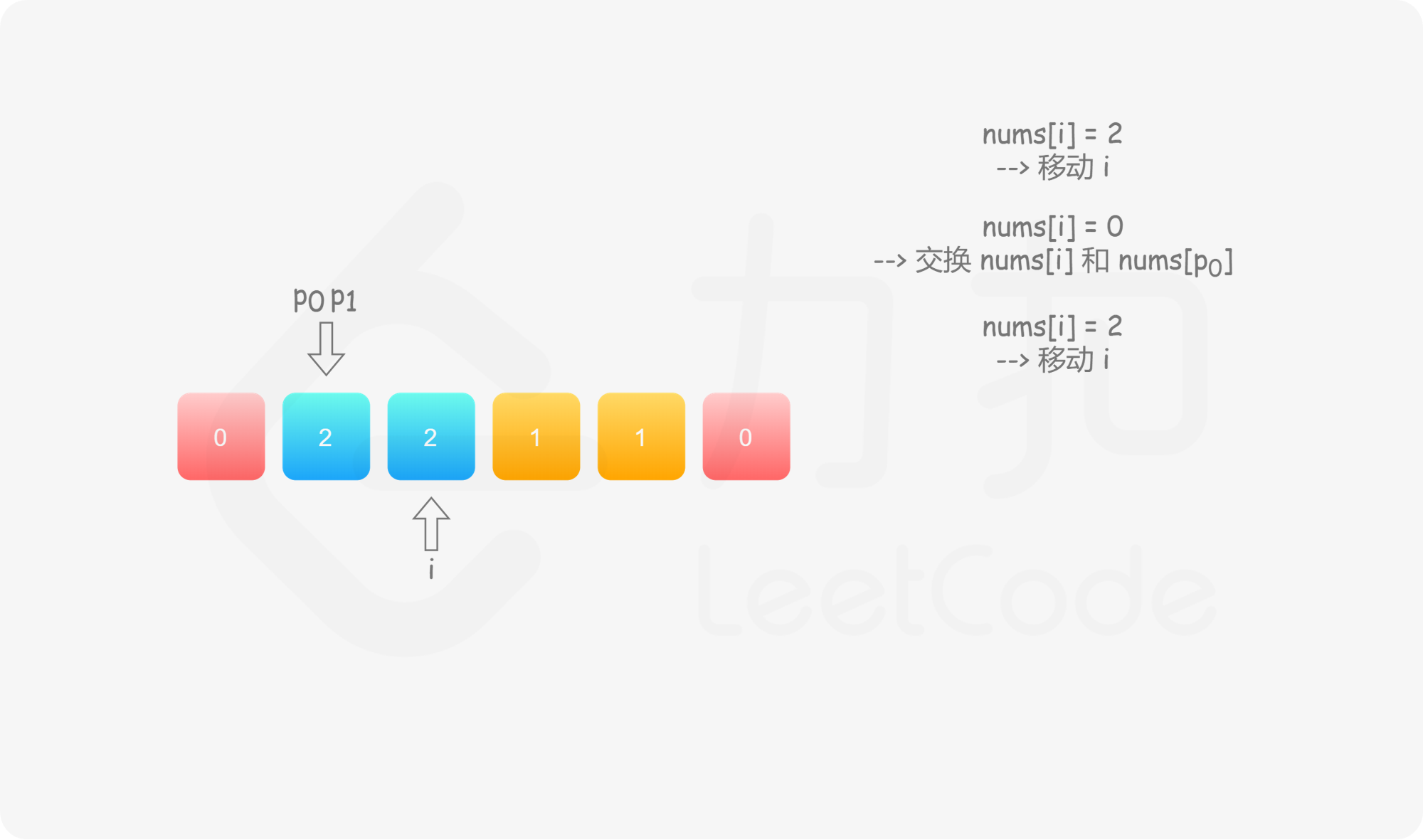
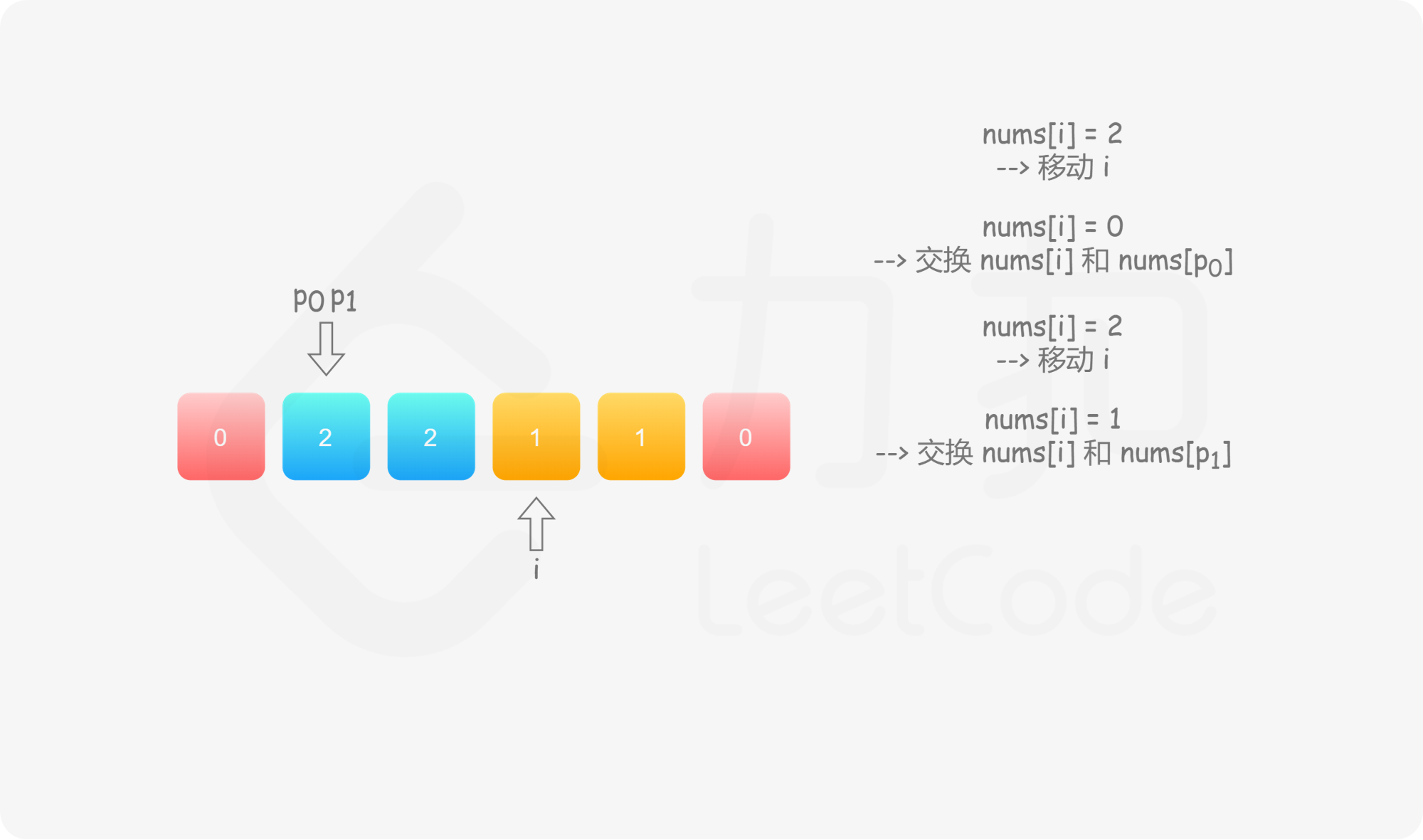
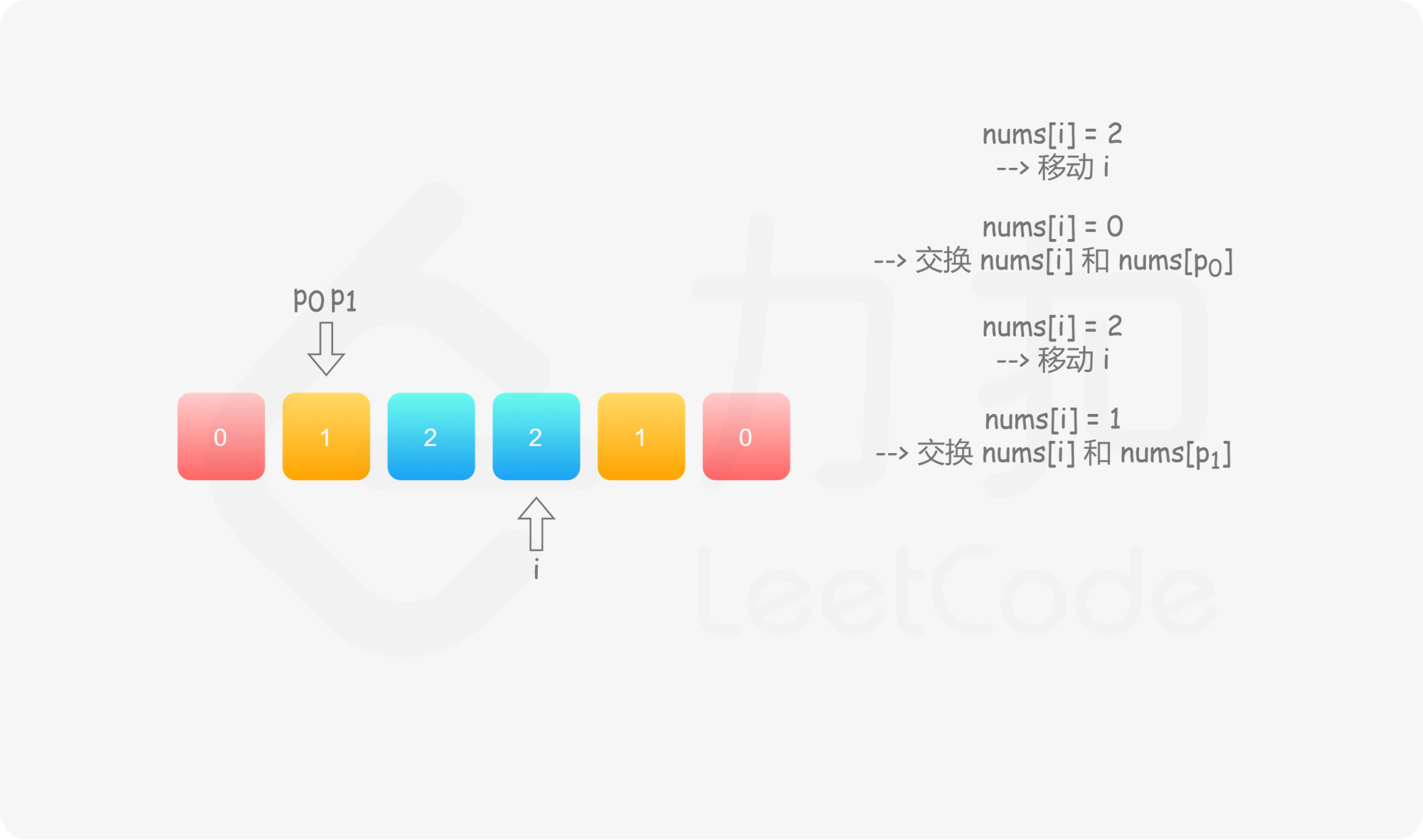
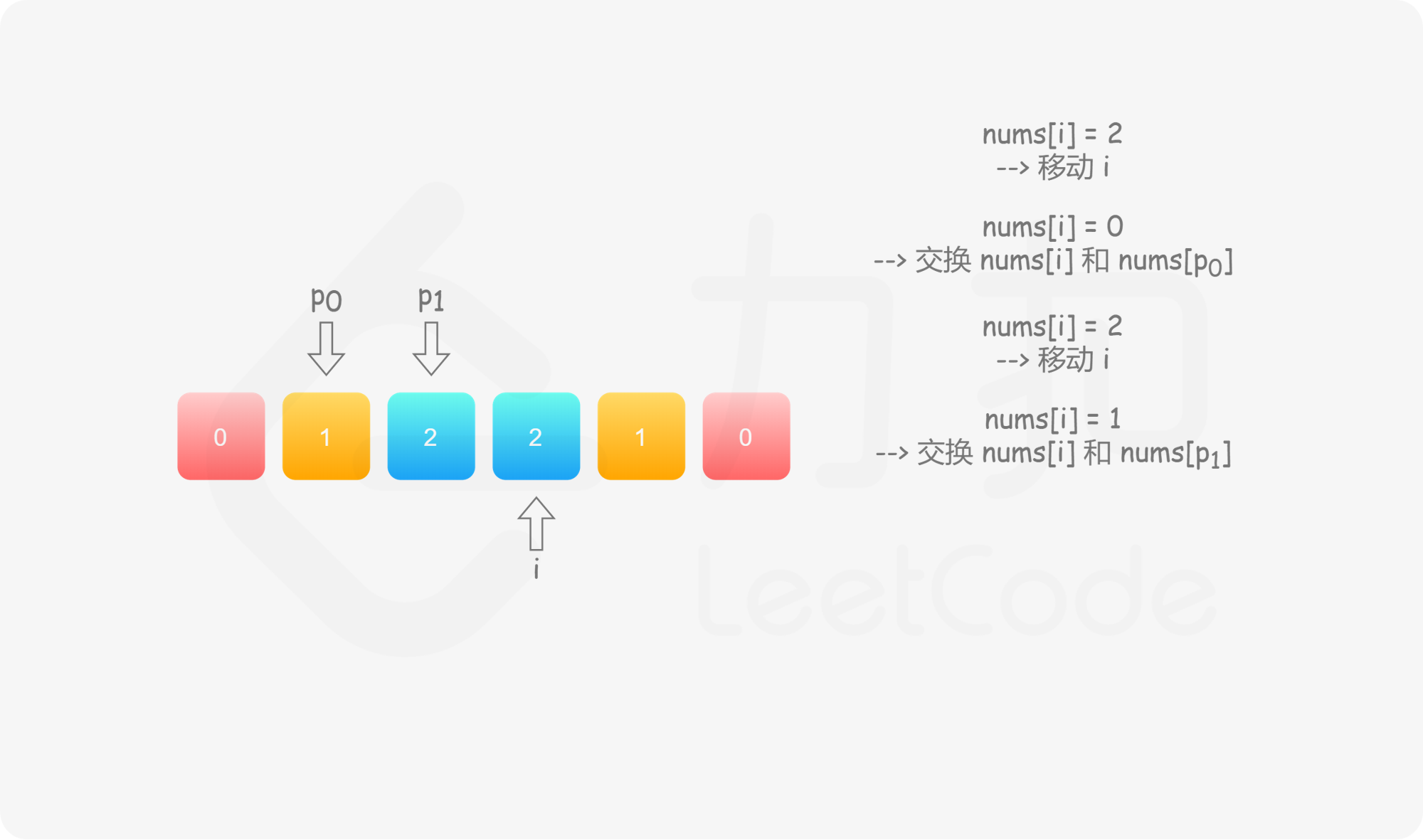
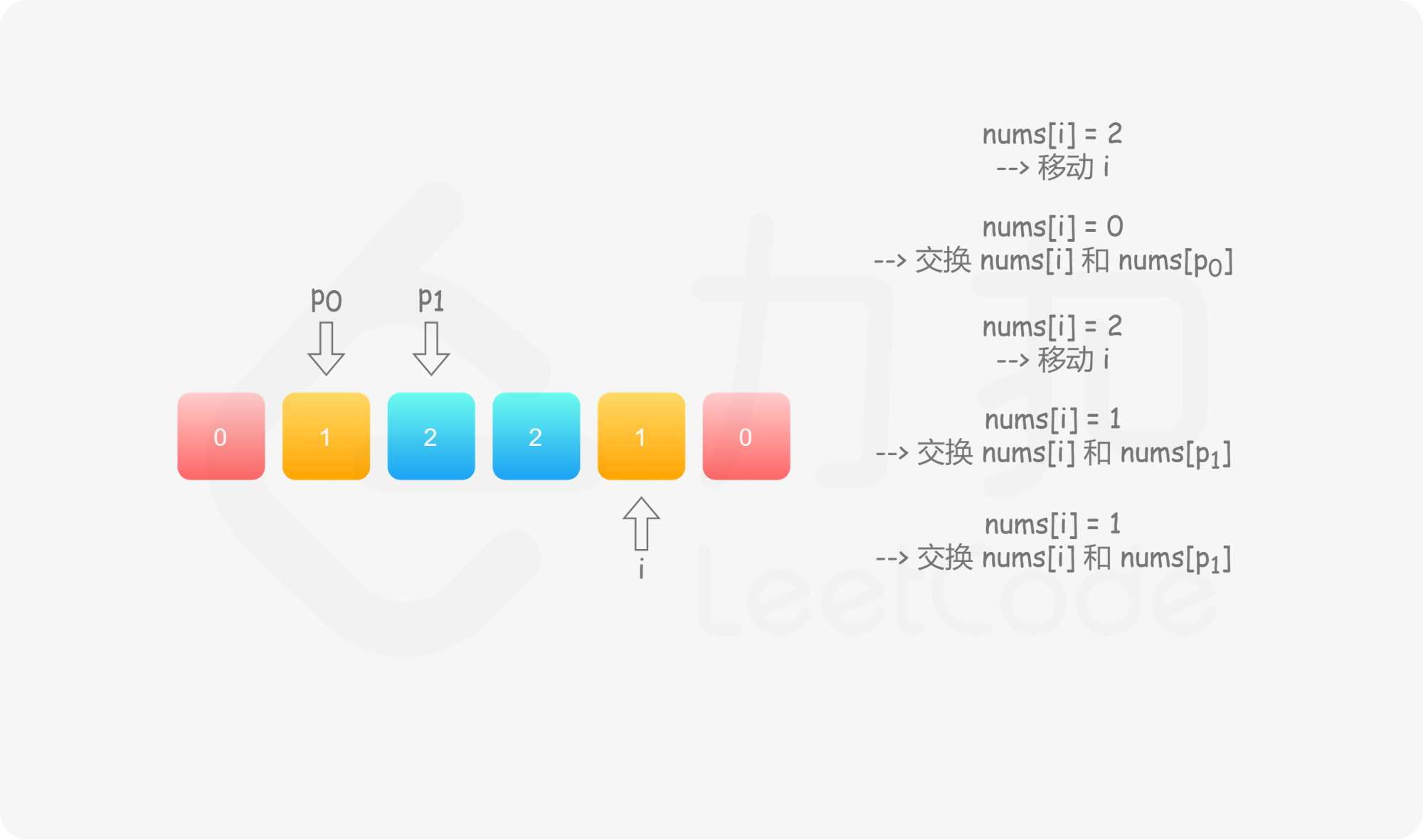
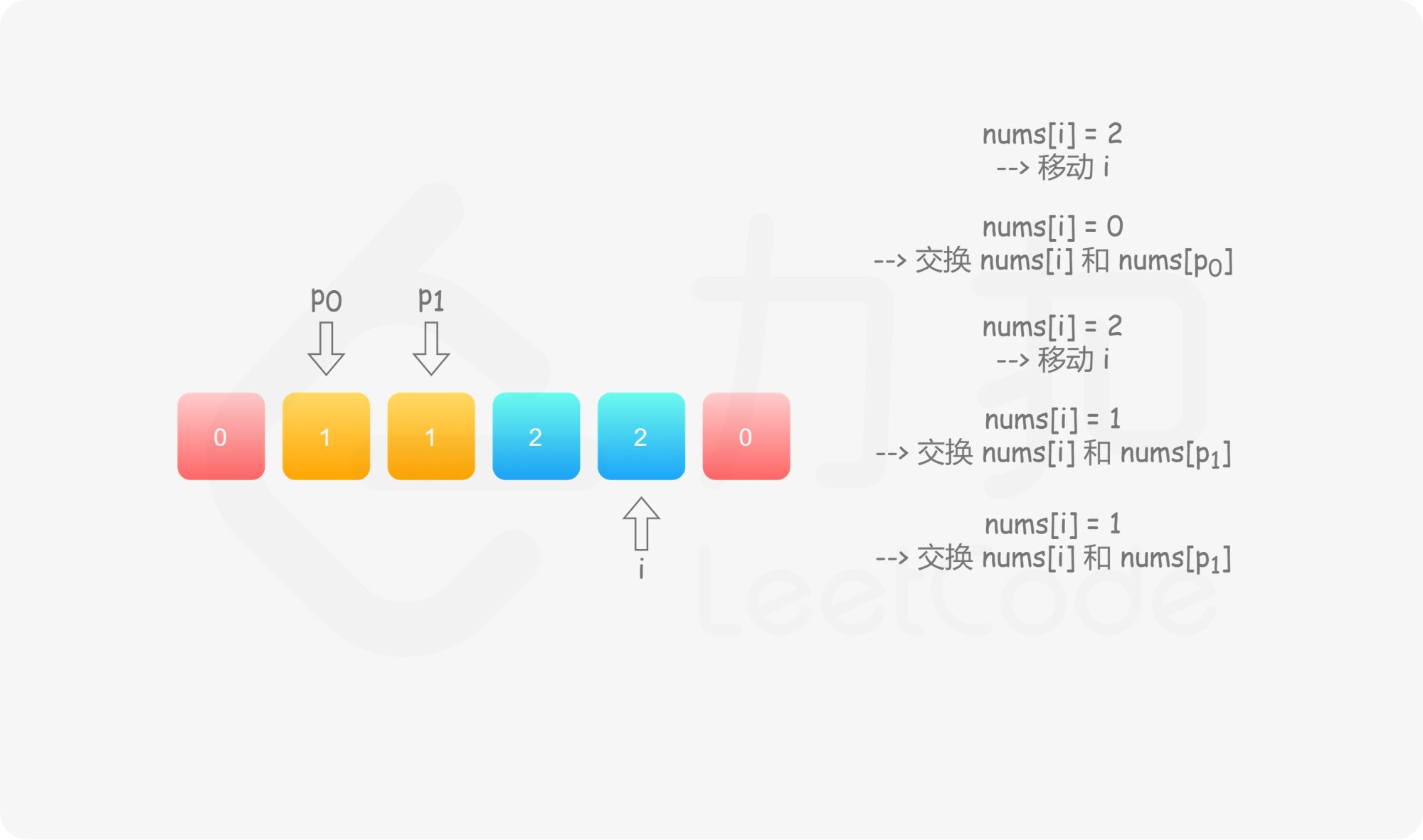
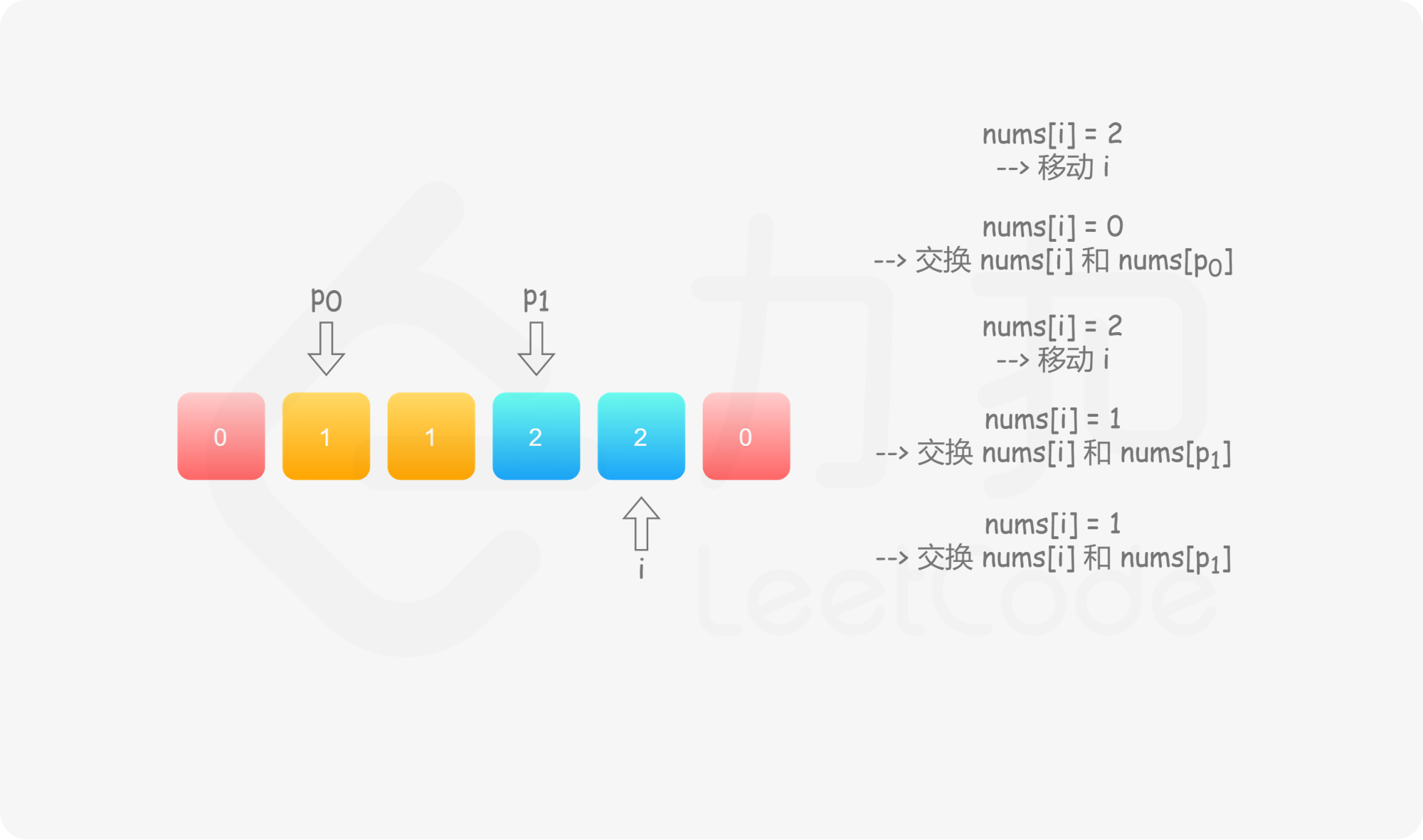
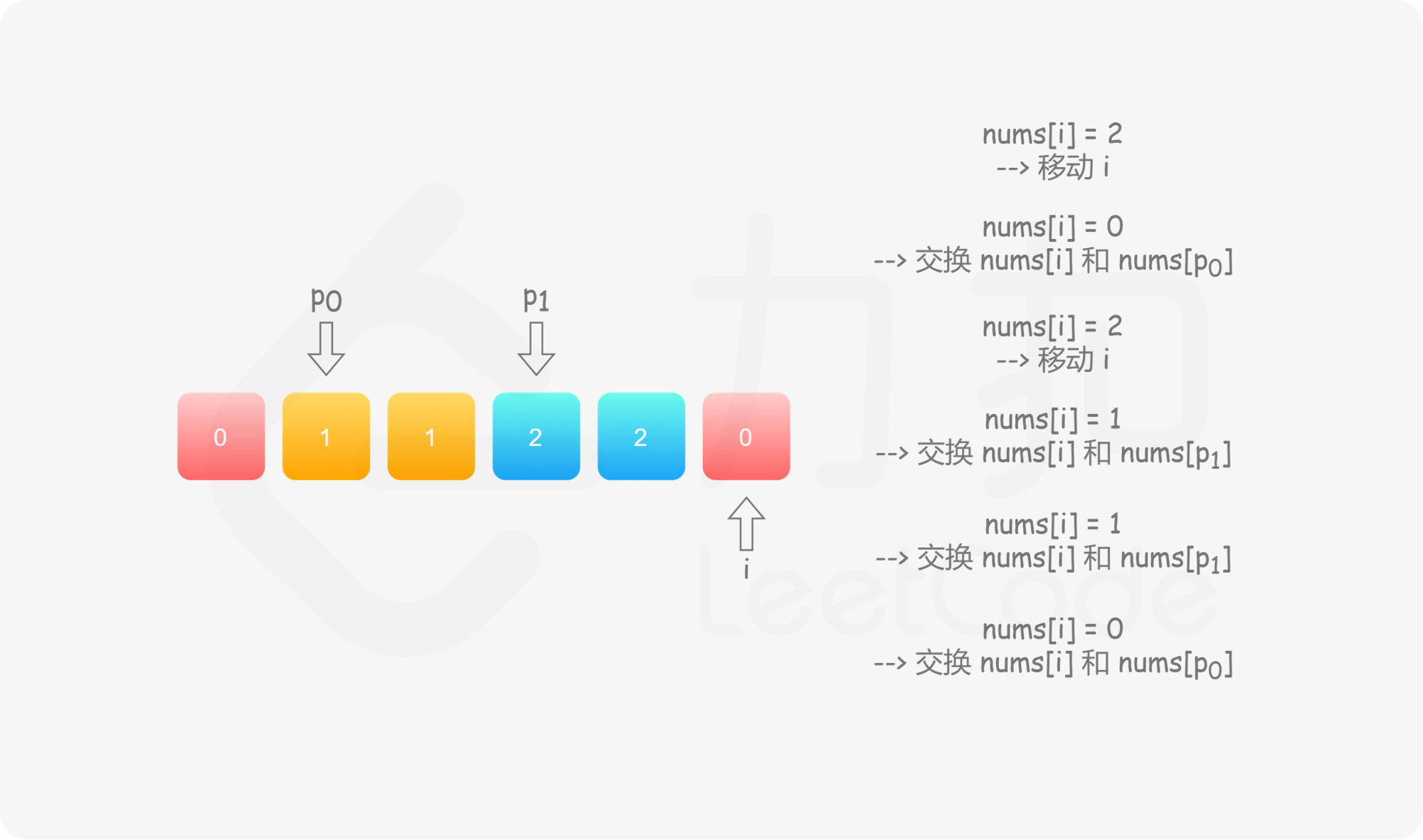
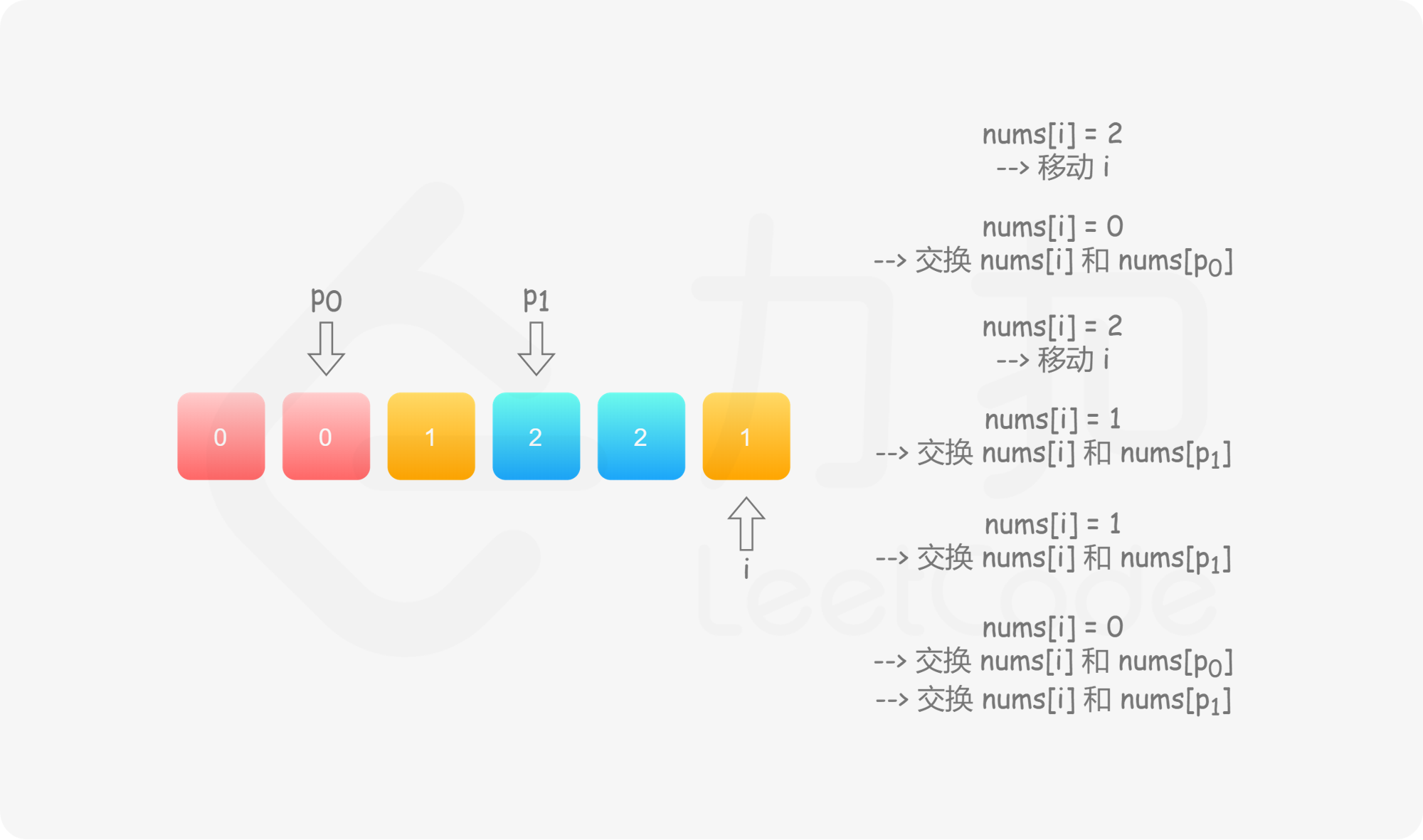
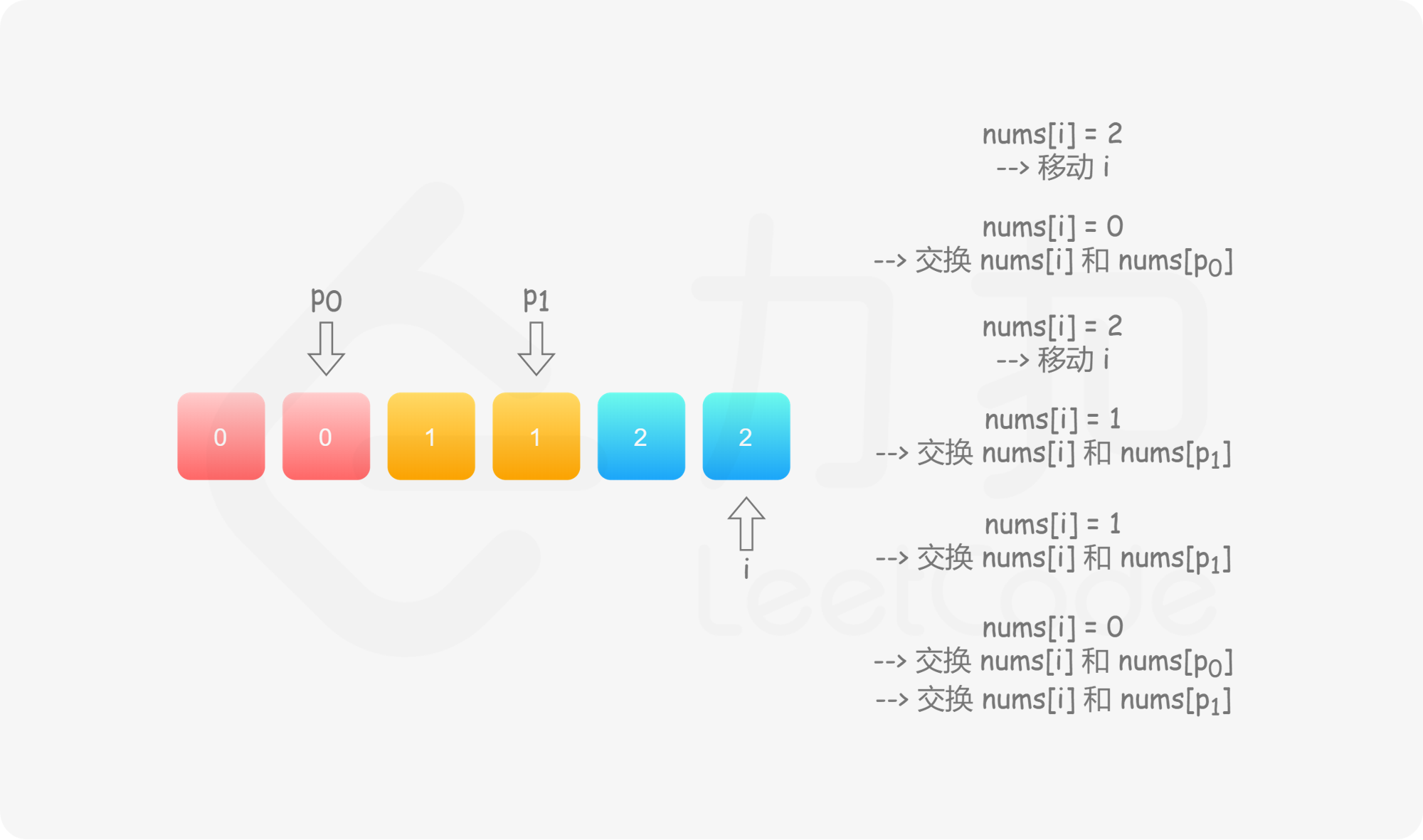
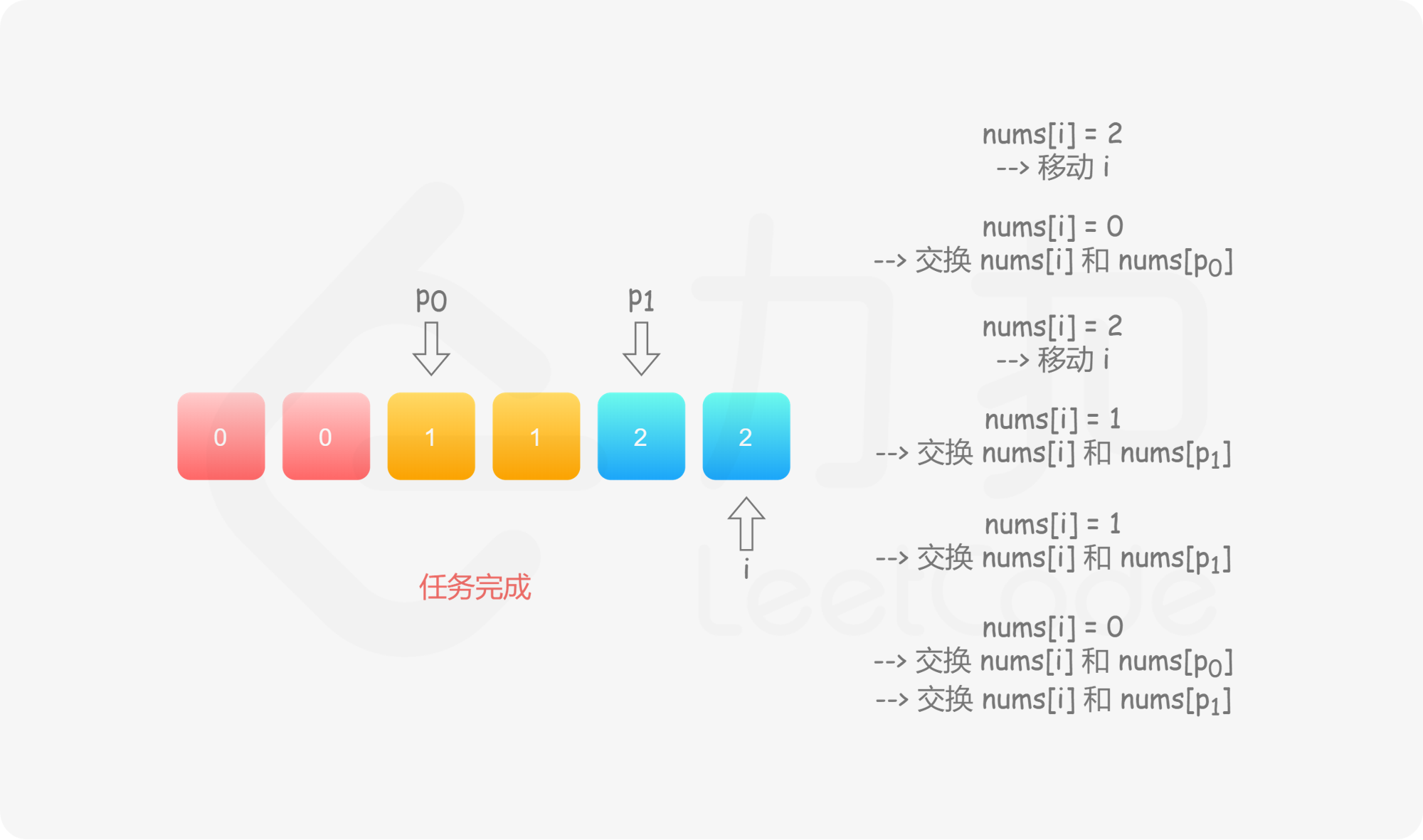
具体地,我们用指针 $p_0$ 来交换 $0$,$p_1$ 来交换 $1$,初始值都为 $0$。当我们从左向右遍历整个数组时:
如果找到了 $1$,那么将其与 $\textit{nums}[p_1]$ 进行交换,并将 $p_1$ 向后移动一个位置,这与方法一是相同的;
如果找到了 $0$,那么将其与 $\textit{nums}[p_0]$ 进行交换,并将 $p_0$ 向后移动一个位置。这样做是正确的吗?我们可以注意到,因为连续的 $0$ 之后是连续的 $1$,因此如果我们将 $0$ 与 $\textit{nums}[p_0]$ 进行交换,那么我们可能会把一个 $1$ 交换出去。当 $p_0 < p_1$ 时,我们已经将一些 $1$ 连续地放在头部,此时一定会把一个 $1$ 交换出去,导致答案错误。因此,如果 $p_0 < p_1$,那么我们需要再将 $\textit{nums}[i]$ 与 $\textit{nums}[p_1]$ 进行交换,其中 $i$ 是当前遍历到的位置,在进行了第一次交换后,$\textit{nums}[i]$ 的值为 $1$,我们需要将这个 $1$ 放到「头部」的末端。在最后,无论是否有 $p_0 < p_1$,我们需要将 $p_0$ 和 $p_1$ 均向后移动一个位置,而不是仅将 $p_0$ 向后移动一个位置。
<
代码
[sol2-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution {public : void sortColors (vector<int >& nums) int n = nums.size (); int p0 = 0 , p1 = 0 ; for (int i = 0 ; i < n; ++i) { if (nums[i] == 1 ) { swap (nums[i], nums[p1]); ++p1; } else if (nums[i] == 0 ) { swap (nums[i], nums[p0]); if (p0 < p1) { swap (nums[i], nums[p1]); } ++p0; ++p1; } } } };
[sol2-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution { public void sortColors (int [] nums) { int n = nums.length; int p0 = 0 , p1 = 0 ; for (int i = 0 ; i < n; ++i) { if (nums[i] == 1 ) { int temp = nums[i]; nums[i] = nums[p1]; nums[p1] = temp; ++p1; } else if (nums[i] == 0 ) { int temp = nums[i]; nums[i] = nums[p0]; nums[p0] = temp; if (p0 < p1) { temp = nums[i]; nums[i] = nums[p1]; nums[p1] = temp; } ++p0; ++p1; } } } }
[sol2-Python3] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution : def sortColors (self, nums: List [int ] ) -> None : n = len (nums) p0 = p1 = 0 for i in range (n): if nums[i] == 1 : nums[i], nums[p1] = nums[p1], nums[i] p1 += 1 elif nums[i] == 0 : nums[i], nums[p0] = nums[p0], nums[i] if p0 < p1: nums[i], nums[p1] = nums[p1], nums[i] p0 += 1 p1 += 1
[sol2-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 func sortColors (nums []int ) p0, p1 := 0 , 0 for i, c := range nums { if c == 0 { nums[i], nums[p0] = nums[p0], nums[i] if p0 < p1 { nums[i], nums[p1] = nums[p1], nums[i] } p0++ p1++ } else if c == 1 { nums[i], nums[p1] = nums[p1], nums[i] p1++ } } }
[sol2-C] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 void swap (int *a, int *b) { int t = *a; *a = *b, *b = t; } void sortColors (int *nums, int numsSize) { int p0 = 0 , p1 = 0 ; for (int i = 0 ; i < numsSize; ++i) { if (nums[i] == 1 ) { swap(&nums[i], &nums[p1]); ++p1; } else if (nums[i] == 0 ) { swap(&nums[i], &nums[p0]); if (p0 < p1) { swap(&nums[i], &nums[p1]); } ++p0; ++p1; } } }
复杂度分析
方法三:双指针 思路与算法
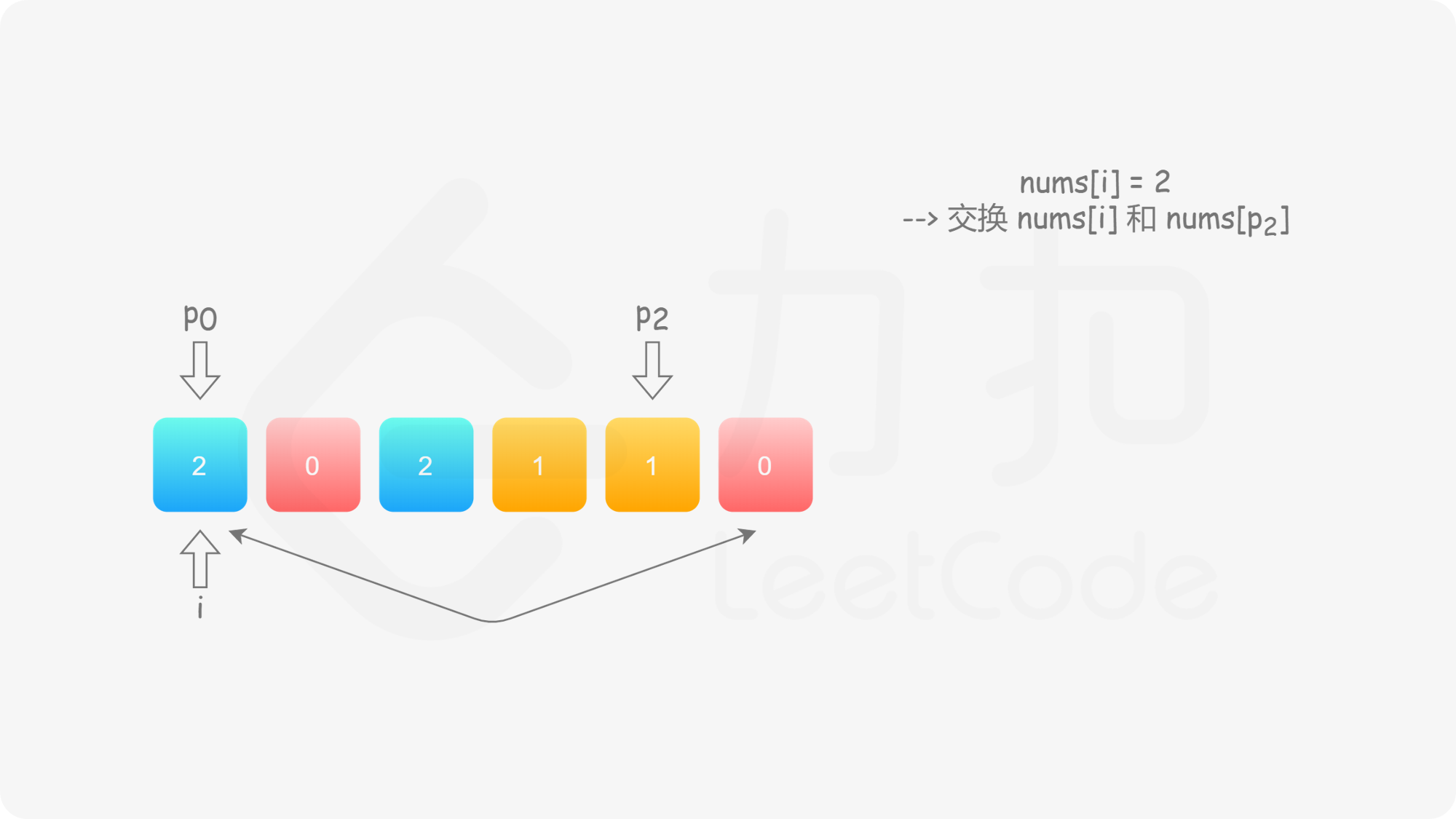
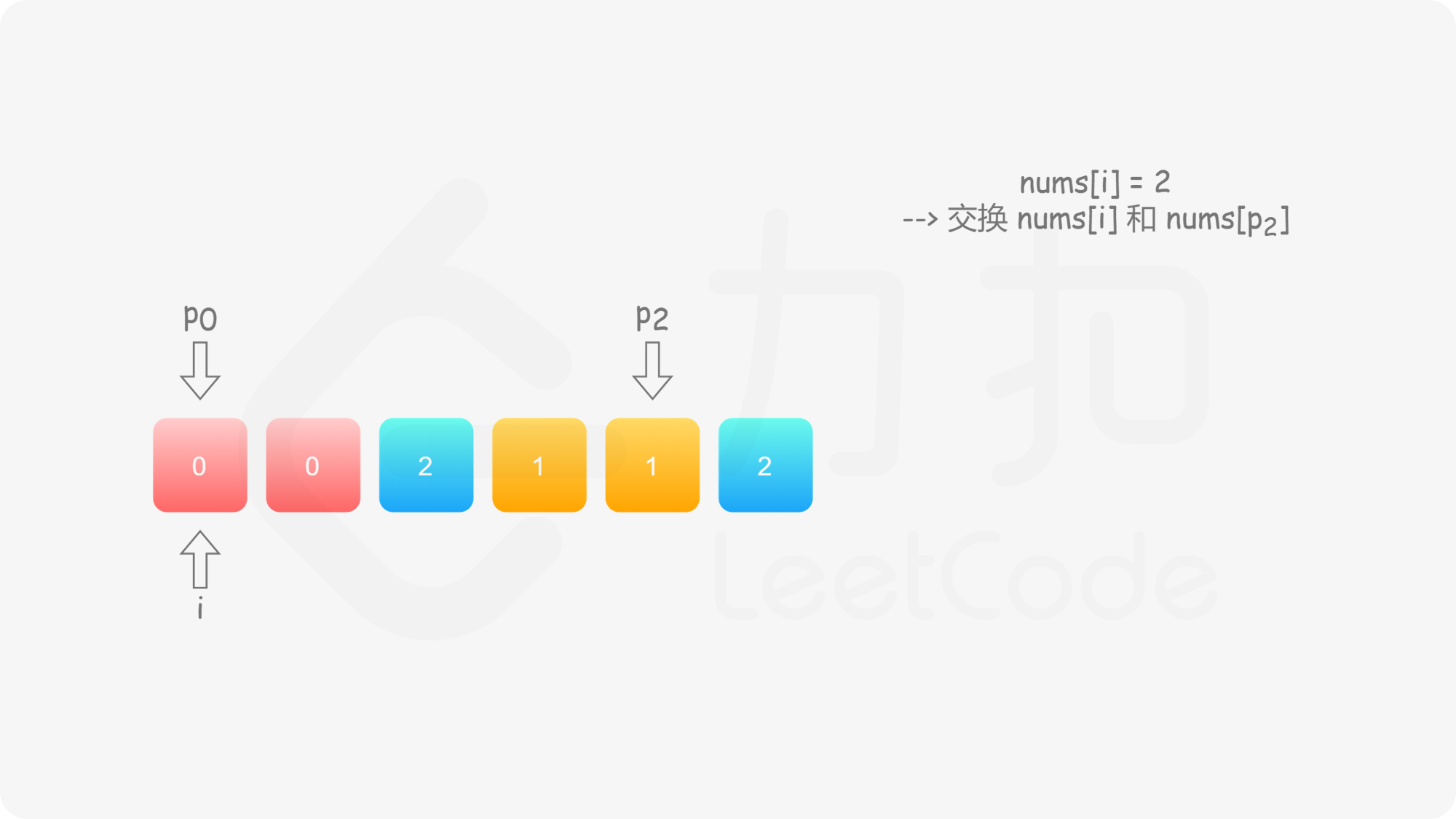
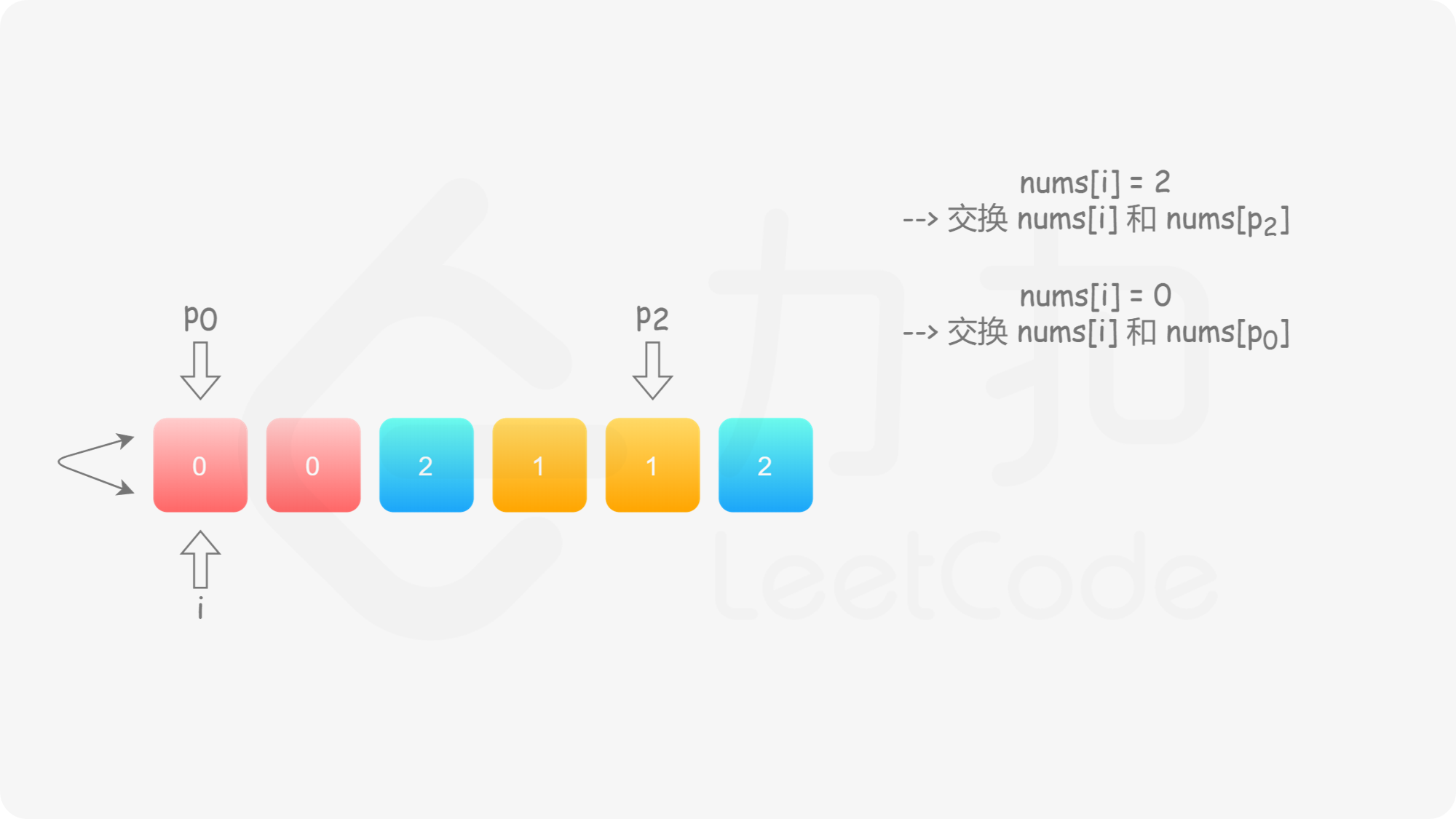
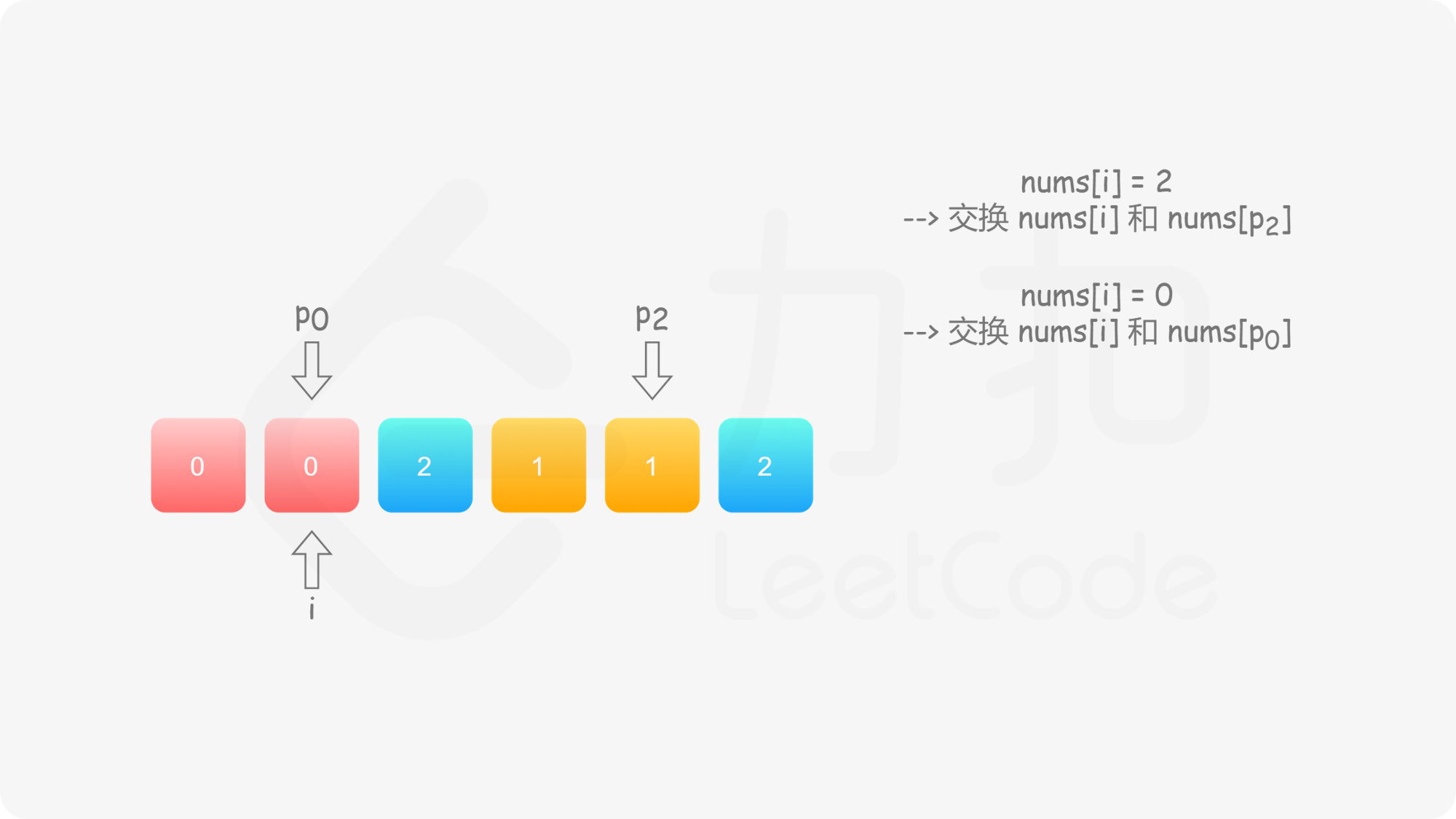
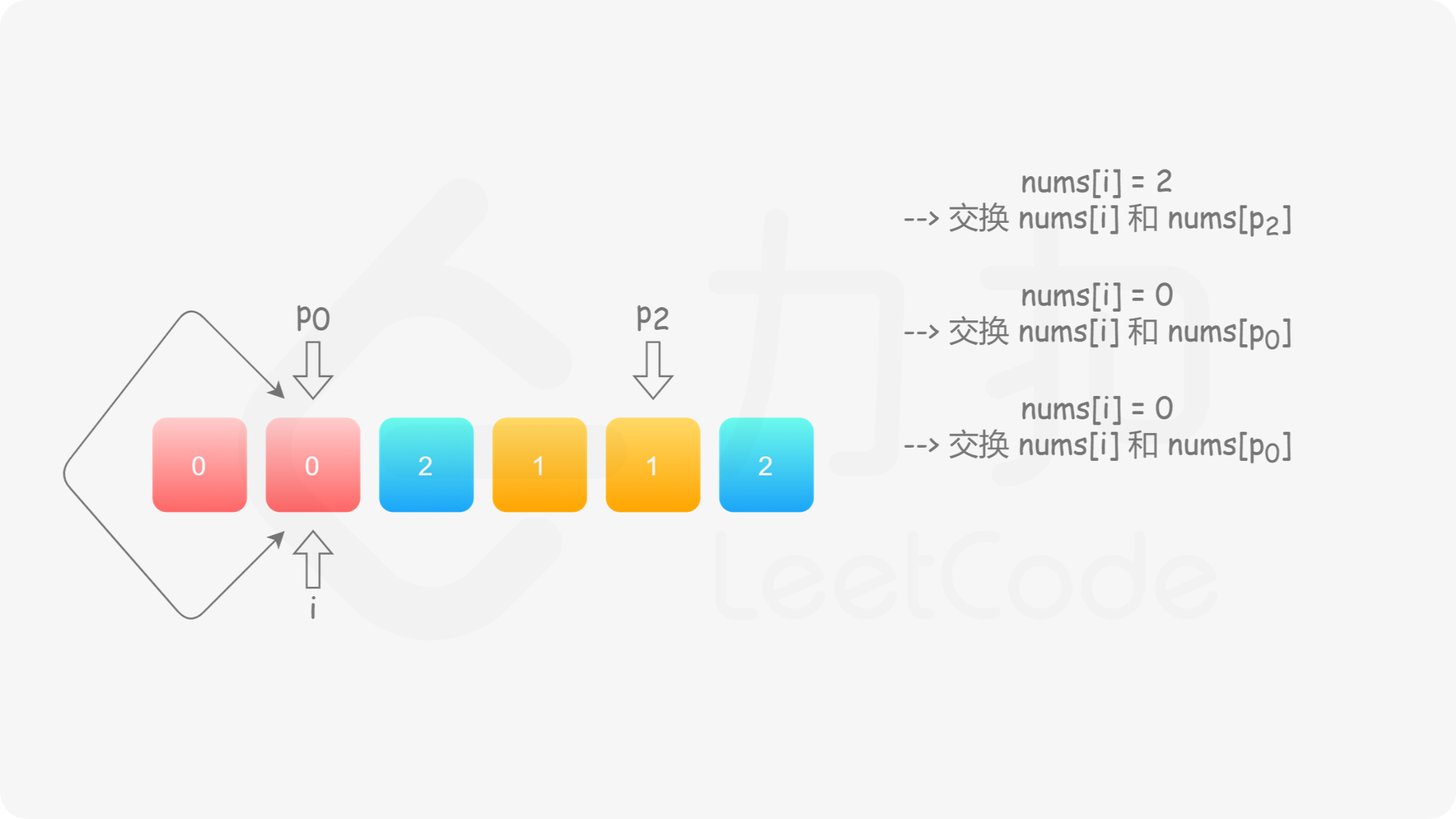
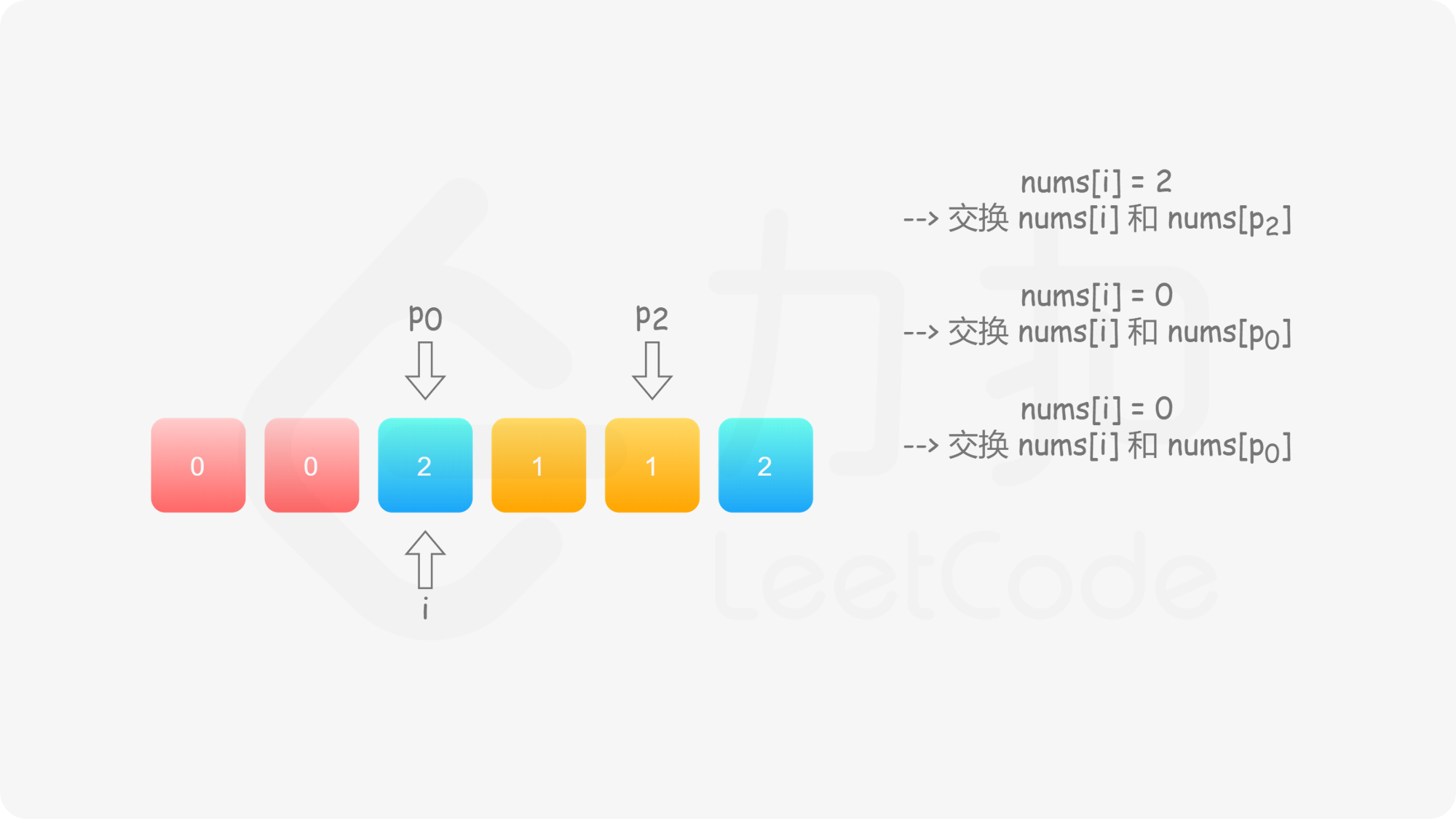
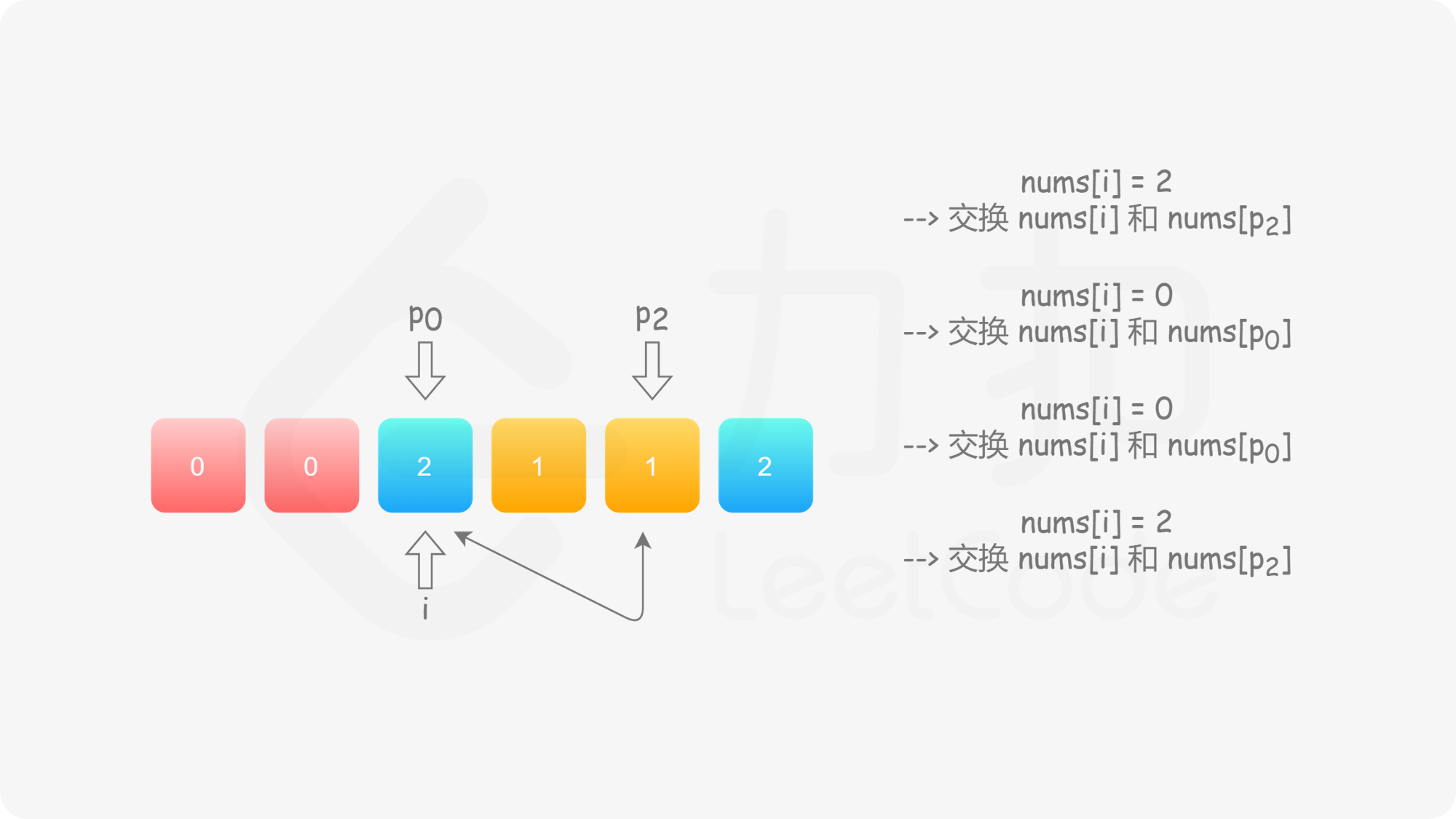
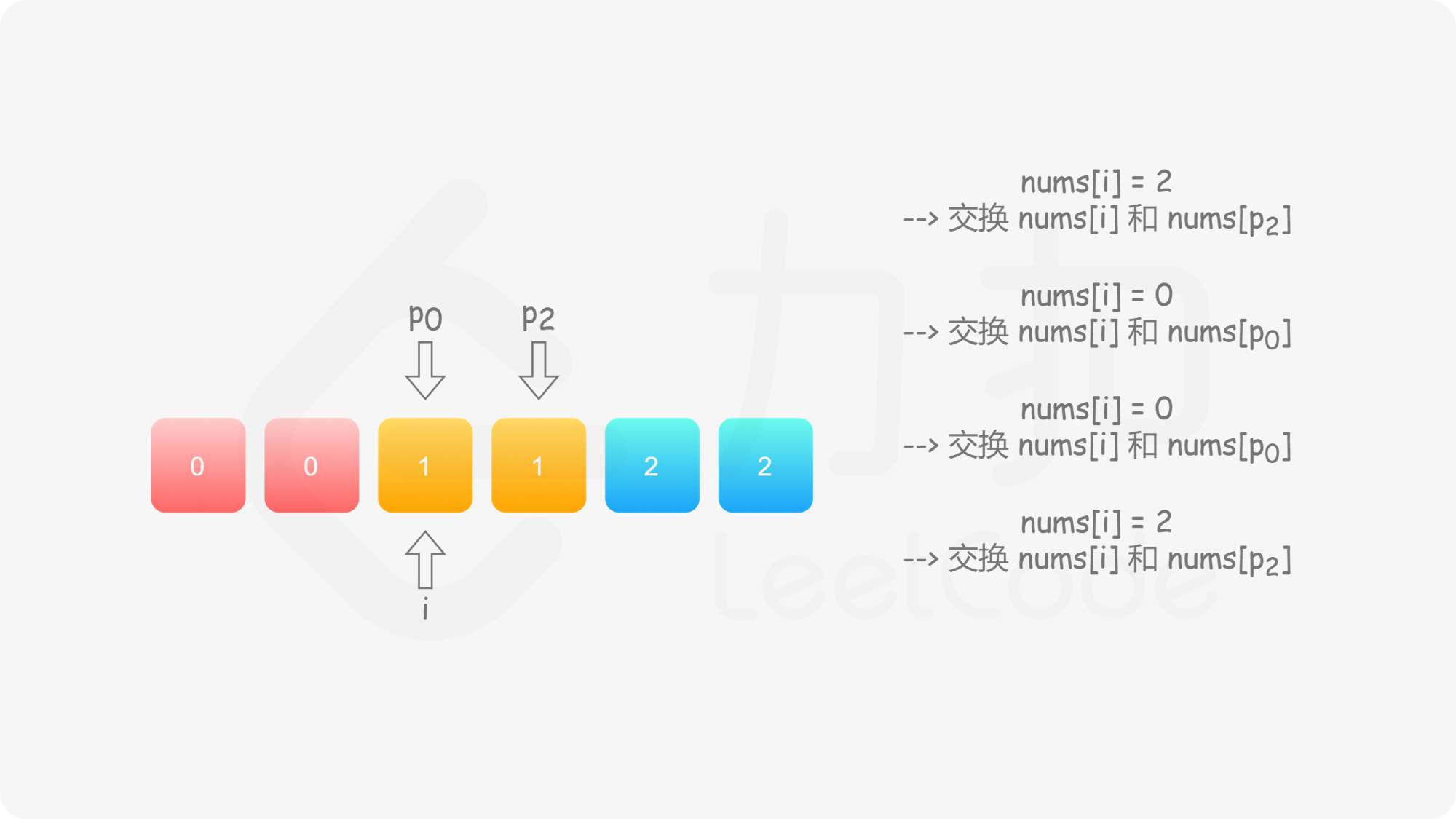
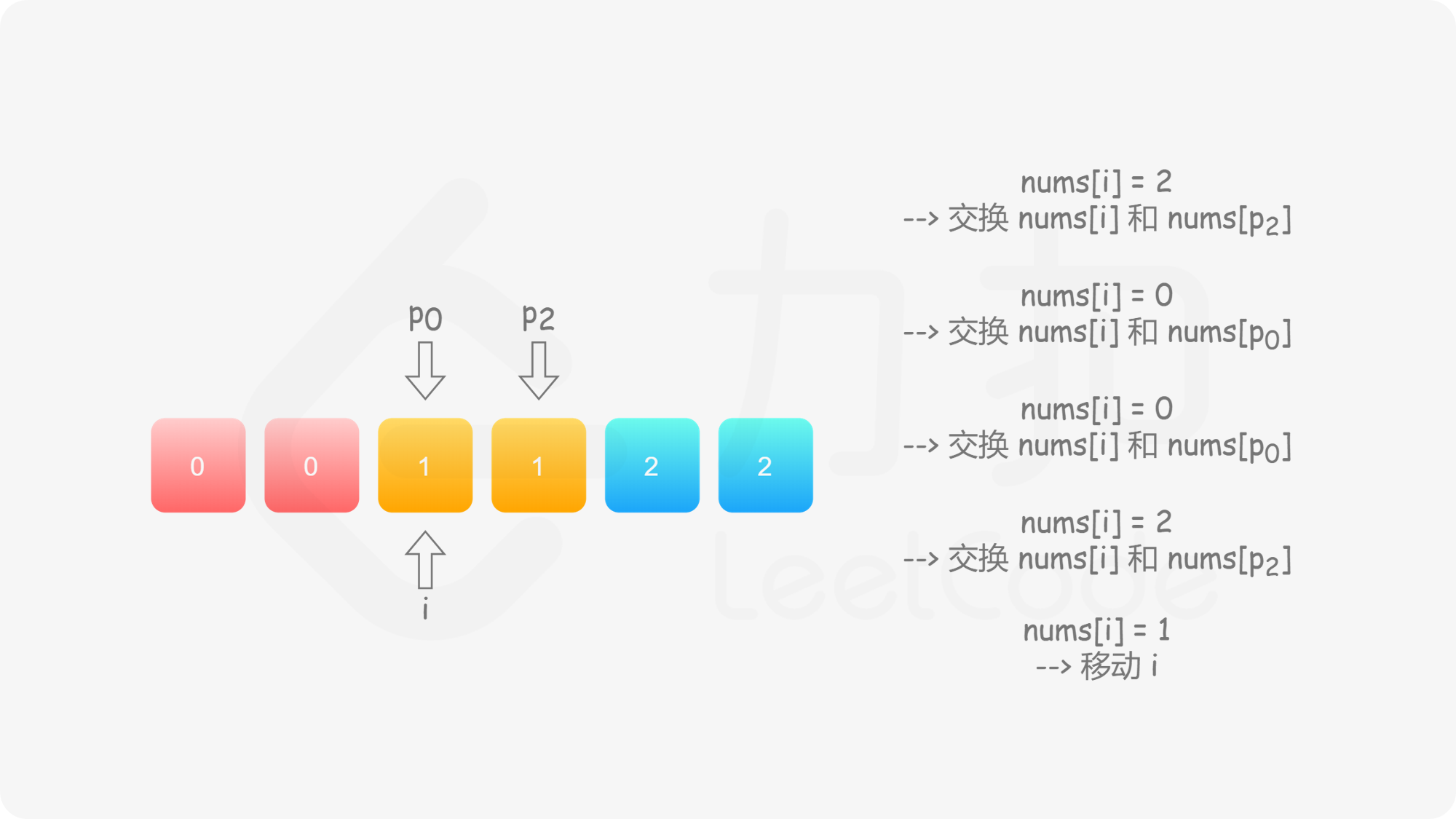
与方法二类似,我们也可以考虑使用指针 $p_0$ 来交换 $0$,$p_2$ 来交换 $2$。此时,$p_0$ 的初始值仍然为 $0$,而 $p_2$ 的初始值为 $n-1$。在遍历的过程中,我们需要找出所有的 $0$ 交换至数组的头部,并且找出所有的 $2$ 交换至数组的尾部。
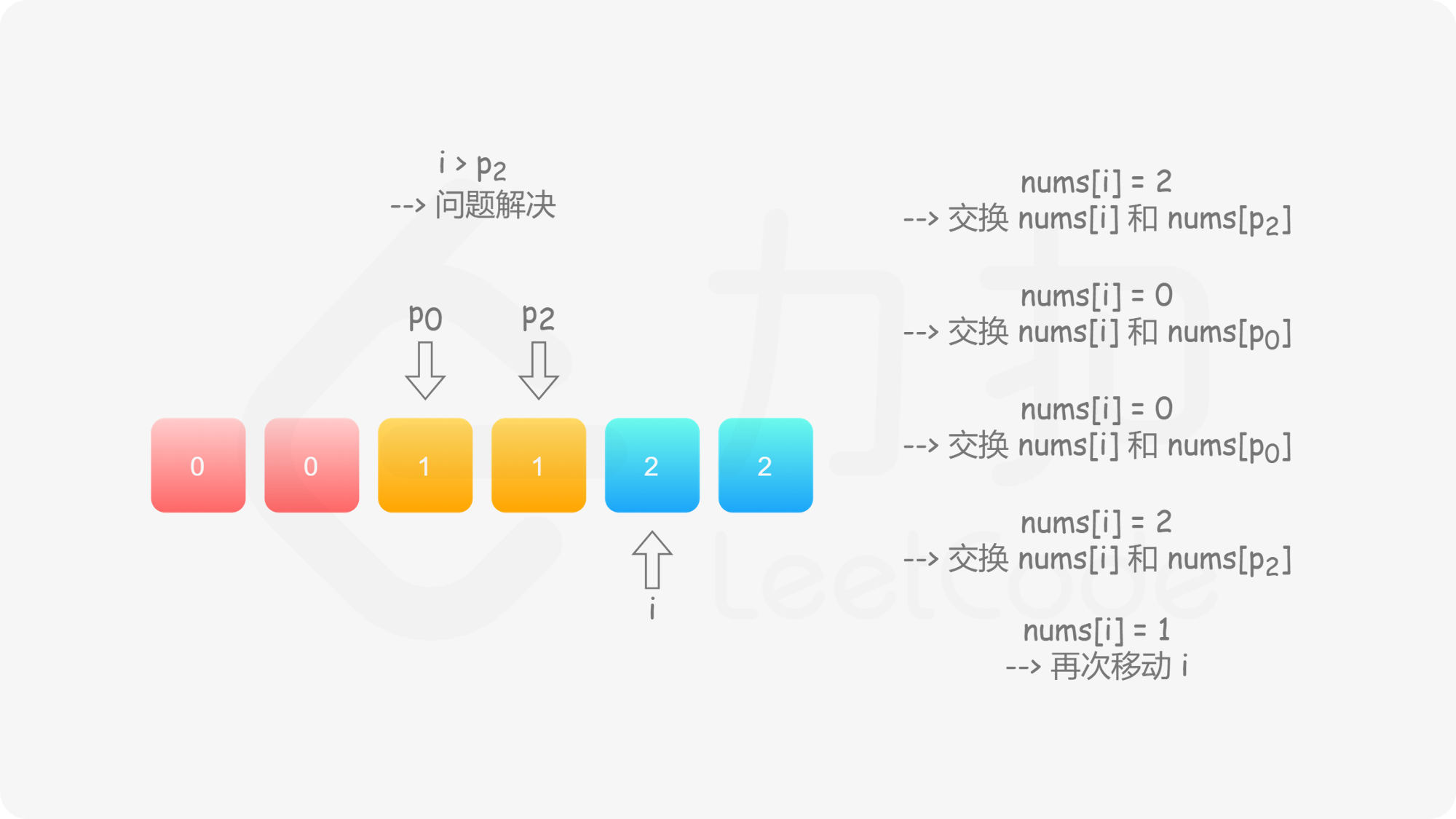
由于此时其中一个指针 $p_2$ 是从右向左 移动的,因此当我们在从左向右 遍历整个数组时,如果遍历到的位置超过了 $p_2$,那么就可以直接停止遍历了。
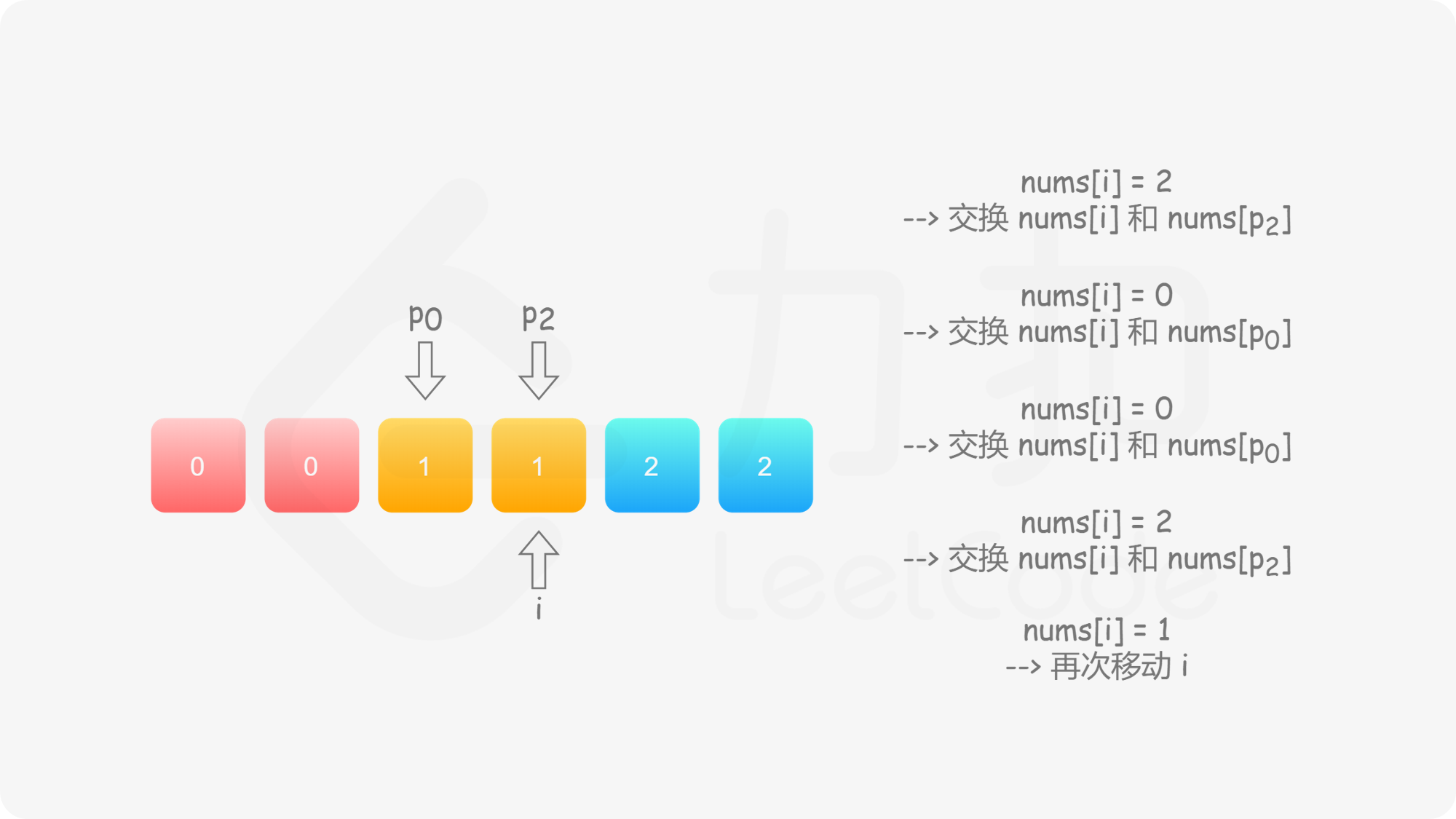
具体地,我们从左向右遍历整个数组,设当前遍历到的位置为 $i$,对应的元素为 $\textit{nums}[i]$;
这样做是正确的吗?可以发现,对于第二种情况,当我们将 $\textit{nums}[i]$ 与 $\textit{nums}[p_2]$ 进行交换之后,新的 $\textit{nums}[i]$ 可能仍然是 $2$,也可能是 $0$。然而此时我们已经结束了交换,开始遍历下一个元素 $\textit{nums}[i+1]$,不会再考虑 $\textit{nums}[i]$ 了,这样我们就会得到错误的答案。
因此,当我们找到 $2$ 时,我们需要不断 地将其与 $\textit{nums}[p_2]$ 进行交换,直到新的 $\textit{nums}[i]$ 不为 $2$。此时,如果 $\textit{nums}[i]$ 为 $0$,那么对应着第一种情况;如果 $\textit{nums}[i]$ 为 $1$,那么就不需要进行任何后续的操作。
<
代码
[sol3-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution {public : void sortColors (vector<int >& nums) int n = nums.size (); int p0 = 0 , p2 = n - 1 ; for (int i = 0 ; i <= p2; ++i) { while (i <= p2 && nums[i] == 2 ) { swap (nums[i], nums[p2]); --p2; } if (nums[i] == 0 ) { swap (nums[i], nums[p0]); ++p0; } } } };
[sol3-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution { public void sortColors (int [] nums) { int n = nums.length; int p0 = 0 , p2 = n - 1 ; for (int i = 0 ; i <= p2; ++i) { while (i <= p2 && nums[i] == 2 ) { int temp = nums[i]; nums[i] = nums[p2]; nums[p2] = temp; --p2; } if (nums[i] == 0 ) { int temp = nums[i]; nums[i] = nums[p0]; nums[p0] = temp; ++p0; } } } }
[sol3-Python3] 1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution : def sortColors (self, nums: List [int ] ) -> None : n = len (nums) p0, p2 = 0 , n - 1 i = 0 while i <= p2: while i <= p2 and nums[i] == 2 : nums[i], nums[p2] = nums[p2], nums[i] p2 -= 1 if nums[i] == 0 : nums[i], nums[p0] = nums[p0], nums[i] p0 += 1 i += 1
[sol3-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 func sortColors (nums []int ) p0, p2 := 0 , len (nums)-1 for i := 0 ; i <= p2; i++ { for ; i <= p2 && nums[i] == 2 ; p2-- { nums[i], nums[p2] = nums[p2], nums[i] } if nums[i] == 0 { nums[i], nums[p0] = nums[p0], nums[i] p0++ } } }
[sol3-C] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 void swap (int *a, int *b) { int t = *a; *a = *b, *b = t; } void sortColors (int *nums, int numsSize) { int p0 = 0 , p2 = numsSize - 1 ; for (int i = 0 ; i <= p2; ++i) { while (i <= p2 && nums[i] == 2 ) { swap(&nums[i], &nums[p2]); --p2; } if (nums[i] == 0 ) { swap(&nums[i], &nums[p0]); ++p0; } } }
复杂度分析
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
> ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>