给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder二叉树 。
示例 1:
**输入:** inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
**输出:** [3,9,20,null,null,15,7]
示例 2:
**输入:** inorder = [-1], postorder = [-1]
**输出:** [-1]
提示:
1 <= inorder.length <= 3000postorder.length == inorder.length-3000 <= inorder[i], postorder[i] <= 3000inorder 和 postorder 都由 不同 的值组成postorder 中每一个值都在 inorder 中inorder 保证 是树的中序遍历postorder 保证 是树的后序遍历
方法一:递归 思路
首先解决这道题我们需要明确给定一棵二叉树,我们是如何对其进行中序遍历与后序遍历的:
中序遍历的顺序是每次遍历左孩子,再遍历根节点,最后遍历右孩子。
后序遍历的顺序是每次遍历左孩子,再遍历右孩子,最后遍历根节点。
写成代码的形式即:
[sol0-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 void inorder (TreeNode* root) if (root == nullptr ) { return ; } inorder (root->left); ans.push_back (root->val); inorder (root->right); } void postorder (TreeNode* root) if (root == nullptr ) { return ; } postorder (root->left); postorder (root->right); ans.push_back (root->val); }
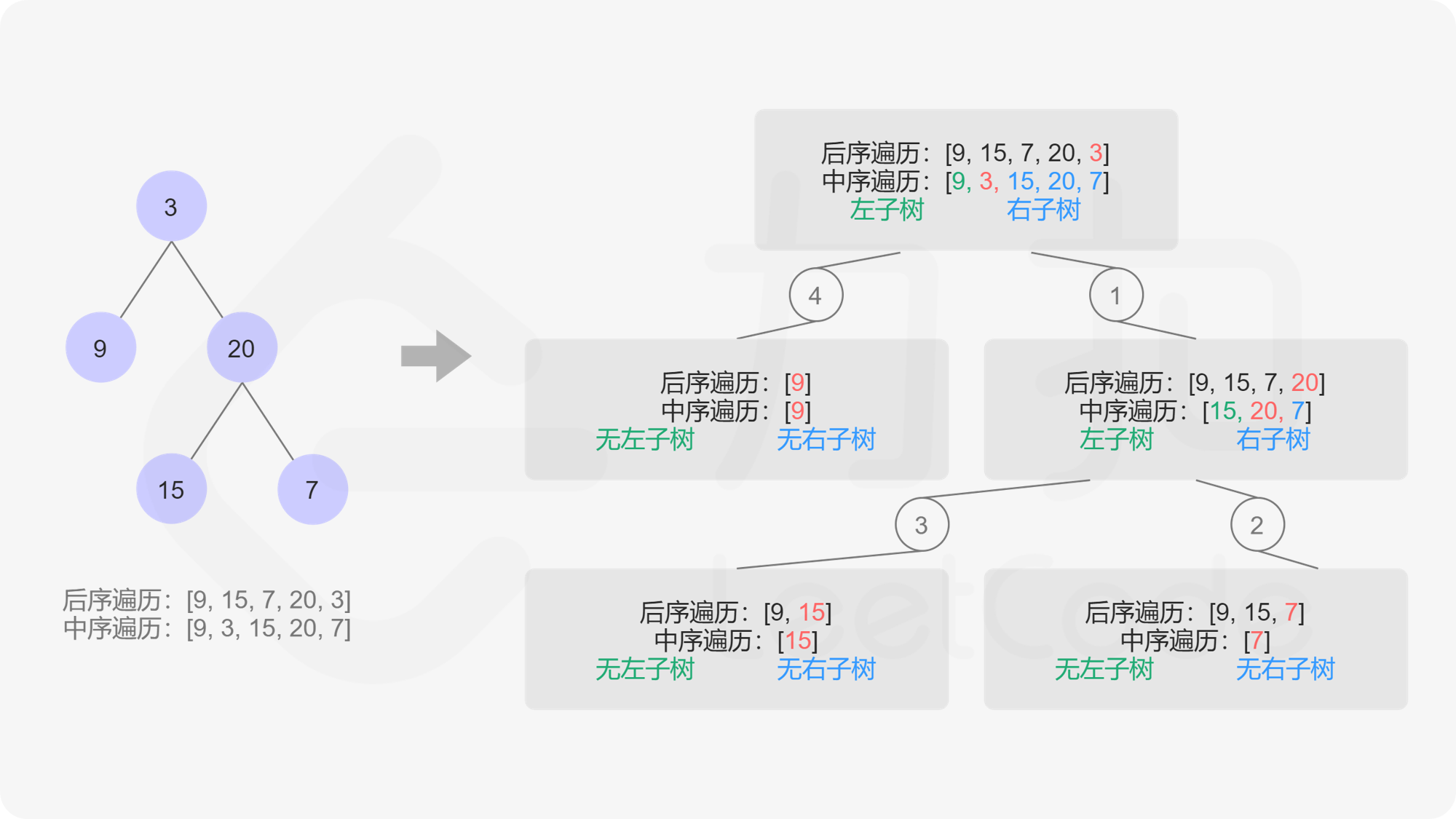
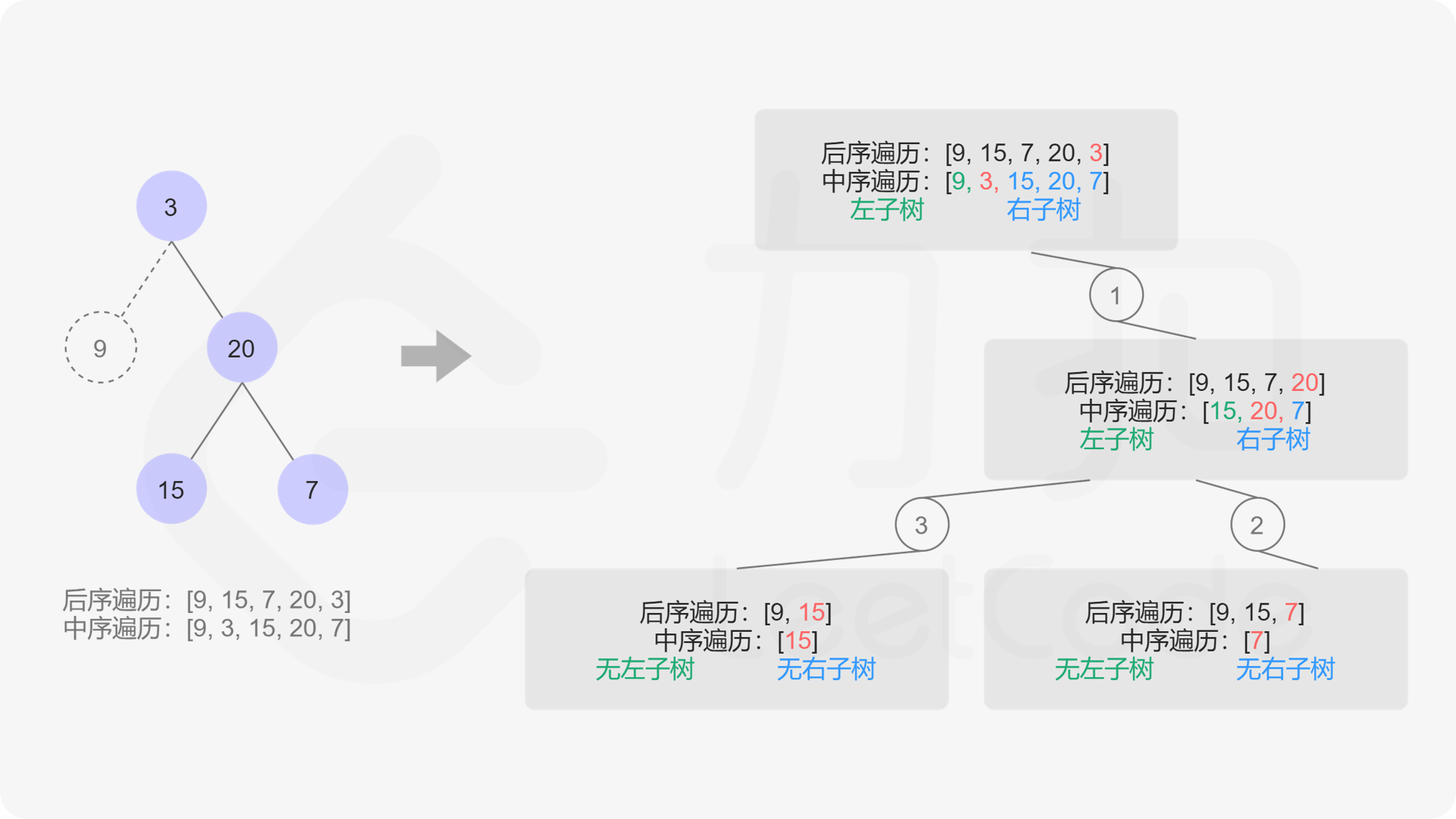
因此根据上文所述,我们可以发现后序遍历的数组最后一个元素代表的即为根节点。知道这个性质后,我们可以利用已知的根节点信息在中序遍历的数组中找到根节点所在的下标,然后根据其将中序遍历的数组分成左右两部分,左边部分即左子树,右边部分为右子树,针对每个部分可以用同样的方法继续递归下去构造。
*算法
为了高效查找根节点元素在中序遍历数组中的下标,我们选择创建哈希表来存储中序序列,即建立一个(元素,下标)键值对的哈希表。
定义递归函数 helper(in_left, in_right) 表示当前递归到中序序列中当前子树的左右边界,递归入口为helper(0, n - 1) :
如果 in_left > in_right,说明子树为空,返回空节点。
选择后序遍历的最后一个节点作为根节点。
利用哈希表 $O(1)$ 查询当根节点在中序遍历中下标为 index。从 in_left 到 index - 1 属于左子树,从 index + 1 到 in_right 属于右子树。
根据后序遍历逻辑,递归创建右子树 helper(index + 1, in_right) 和左子树 helper(in_left, index - 1)。注意这里有需要先创建右子树,再创建左子树的依赖关系。可以理解为在后序遍历的数组中整个数组是先存储左子树的节点,再存储右子树的节点,最后存储根节点,如果按每次选择「后序遍历的最后一个节点」为根节点,则先被构造出来的应该为右子树。
返回根节点 root。
<
代码
[sol1-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 class Solution { int post_idx; int [] postorder; int [] inorder; Map<Integer, Integer> idx_map = new HashMap <Integer, Integer>(); public TreeNode helper (int in_left, int in_right) { if (in_left > in_right) { return null ; } int root_val = postorder[post_idx]; TreeNode root = new TreeNode (root_val); int index = idx_map.get(root_val); post_idx--; root.right = helper(index + 1 , in_right); root.left = helper(in_left, index - 1 ); return root; } public TreeNode buildTree (int [] inorder, int [] postorder) { this .postorder = postorder; this .inorder = inorder; post_idx = postorder.length - 1 ; int idx = 0 ; for (Integer val : inorder) { idx_map.put(val, idx++); } return helper(0 , inorder.length - 1 ); } }
[sol1-Python3] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution : def buildTree (self, inorder: List [int ], postorder: List [int ] ) -> TreeNode: def helper (in_left, in_right ): if in_left > in_right: return None val = postorder.pop() root = TreeNode(val) index = idx_map[val] root.right = helper(index + 1 , in_right) root.left = helper(in_left, index - 1 ) return root idx_map = {val:idx for idx, val in enumerate (inorder)} return helper(0 , len (inorder) - 1 )
[sol1-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 class Solution { int post_idx; unordered_map<int , int > idx_map; public : TreeNode* helper (int in_left, int in_right, vector<int >& inorder, vector<int >& postorder) { if (in_left > in_right) { return nullptr ; } int root_val = postorder[post_idx]; TreeNode* root = new TreeNode (root_val); int index = idx_map[root_val]; post_idx--; root->right = helper (index + 1 , in_right, inorder, postorder); root->left = helper (in_left, index - 1 , inorder, postorder); return root; } TreeNode* buildTree (vector<int >& inorder, vector<int >& postorder) { post_idx = (int )postorder.size () - 1 ; int idx = 0 ; for (auto & val : inorder) { idx_map[val] = idx++; } return helper (0 , (int )inorder.size () - 1 , inorder, postorder); } };
[sol1-JavaScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 var buildTree = function (inorder, postorder ) { let post_idx; const idx_map = new Map (); const helper = (in_left, in_right ) => { if (in_left > in_right) { return null ; } const root_val = postorder[post_idx]; const root = new TreeNode (root_val); const index = idx_map.get (root_val); post_idx--; root.right = helper (index + 1 , in_right); root.left = helper (in_left, index - 1 ); return root; } post_idx = postorder.length - 1 ; let idx = 0 ; inorder.forEach ((val, idx ) => { idx_map.set (val, idx); }); return helper (0 , inorder.length - 1 ); };
[sol1-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 func buildTree (inorder []int , postorder []int ) idxMap := map [int ]int {} for i, v := range inorder { idxMap[v] = i } var build func (int , int ) build = func (inorderLeft, inorderRight int ) if inorderLeft > inorderRight { return nil } val := postorder[len (postorder)-1 ] postorder = postorder[:len (postorder)-1 ] root := &TreeNode{Val: val} inorderRootIndex := idxMap[val] root.Right = build(inorderRootIndex+1 , inorderRight) root.Left = build(inorderLeft, inorderRootIndex-1 ) return root } return build(0 , len (inorder)-1 ) }
[sol1-C] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 int post_idx;typedef struct { int key; int val; UT_hash_handle hh; } hashTable; hashTable* idx_map; void insertHashTable (int x, int y) { hashTable* rec = malloc (sizeof (hashTable)); rec->key = x; rec->val = y; HASH_ADD_INT(idx_map, key, rec); } int queryHashTable (int x) { hashTable* rec; HASH_FIND_INT(idx_map, &x, rec); return rec->val; } struct TreeNode* helper (int in_left, int in_right, int * inorder, int * postorder) { if (in_left > in_right) { return NULL ; } int root_val = postorder[post_idx]; struct TreeNode * root =malloc (sizeof (struct TreeNode)); root->val = root_val; int index = queryHashTable(root_val); post_idx--; root->right = helper(index + 1 , in_right, inorder, postorder); root->left = helper(in_left, index - 1 , inorder, postorder); return root; } struct TreeNode* buildTree (int * inorder, int inorderSize, int * postorder, int postorderSize) { post_idx = postorderSize - 1 ; idx_map = NULL ; int idx = 0 ; for (int i = 0 ; i < inorderSize; i++) { insertHashTable(inorder[i], idx++); } return helper(0 , inorderSize - 1 , inorder, postorder); }
复杂度分析
方法二:迭代 思路
迭代法是一种非常巧妙的实现方法。迭代法的实现基于以下两点发现。
如果将中序遍历反序,则得到反向的中序遍历,即每次遍历右孩子,再遍历根节点,最后遍历左孩子。
如果将后序遍历反序,则得到反向的前序遍历,即每次遍历根节点,再遍历右孩子,最后遍历左孩子。
「反向」的意思是交换遍历左孩子和右孩子的顺序,即反向的遍历中,右孩子在左孩子之前被遍历。
因此可以使用和「105. 从前序与中序遍历序列构造二叉树 」的迭代方法类似的方法构造二叉树。
对于后序遍历中的任意两个连续节点 $u$ 和 $v$(在后序遍历中,$u$ 在 $v$ 的前面),根据后序遍历的流程,我们可以知道 $u$ 和 $v$ 只有两种可能的关系:
$u$ 是 $v$ 的右儿子。这是因为在遍历到 $u$ 之后,下一个遍历的节点就是 $u$ 的双亲节点,即 $v$;
$v$ 没有右儿子,并且 $u$ 是 $v$ 的某个祖先节点(或者 $v$ 本身)的左儿子。如果 $v$ 没有右儿子,那么上一个遍历的节点就是 $v$ 的左儿子。如果 $v$ 没有左儿子,则从 $v$ 开始向上遍历 $v$ 的祖先节点,直到遇到一个有左儿子(且 $v$ 不在它的左儿子的子树中)的节点 $v_a$,那么 $u$ 就是 $v_a$ 的左儿子。
第二种关系看上去有些复杂。我们举一个例子来说明其正确性,并在例子中给出我们的迭代算法。
例子
我们以树
1 2 3 4 5 6 7 8 9 3 / \ 9 20 / \ \ 15 10 7 / \ 5 8 \ 4
为例,它的中序遍历和后序遍历分别为
1 2 inorder = [15, 9, 10, 3, 20, 5, 7, 8, 4] postorder = [15, 10, 9, 5, 4, 8, 7, 20, 3]
我们用一个栈 stack 来维护「当前节点的所有还没有考虑过左儿子的祖先节点」,栈顶就是当前节点。也就是说,只有在栈中的节点才可能连接一个新的左儿子。同时,我们用一个指针 index 指向中序遍历的某个位置,初始值为 n - 1,其中 n 为数组的长度。index 对应的节点是「当前节点不断往右走达到的最终节点」,这也是符合反向中序遍历的,它的作用在下面的过程中会有所体现。
首先我们将根节点 3 入栈,再初始化 index 所指向的节点为 4,随后对于后序遍历中的每个节点,我们依次判断它是栈顶节点的右儿子,还是栈中某个节点的左儿子。
我们遍历 20。20 一定是栈顶节点 3 的右儿子。我们使用反证法,假设 20 是 3 的左儿子,因为 20 和 3 中间不存在其他的节点,那么 3 没有右儿子,index 应该恰好指向 3,但实际上为 4,因此产生了矛盾。所以我们将 20 作为 3 的右儿子,并将 20 入栈。
stack = [3, 20]index -> inorder[8] = 4
我们遍历 7,8 和 4。同理可得它们都是上一个节点(栈顶节点)的右儿子,所以它们会依次入栈。
stack = [3, 20, 7, 8, 4]index -> inorder[8] = 4
我们遍历 5,这时情况就不一样了。我们发现 index 恰好指向当前的栈顶节点 4,也就是说 4 没有右儿子,那么 5 必须为栈中某个节点的左儿子。那么如何找到这个节点呢?栈中的节点的顺序和它们在反向前序遍历中出现的顺序是一致的,而且每一个节点的左儿子都还没有被遍历过,那么这些节点的顺序和它们在反向中序遍历中出现的顺序一定是相反的 。
这是因为栈中的任意两个相邻的节点,前者都是后者的某个祖先。并且我们知道,栈中的任意一个节点的左儿子还没有被遍历过,说明后者一定是前者右儿子的子树中的节点,那么后者就先于前者出现在反向中序遍历中。
因此我们可以把 index 不断向左移动,并与栈顶节点进行比较。如果 index 对应的元素恰好等于栈顶节点,那么说明我们在反向中序遍历中找到了栈顶节点,所以将 index 减少 1 并弹出栈顶节点,直到 index 对应的元素不等于栈顶节点。按照这样的过程,我们弹出的最后一个节点 x 就是 5 的双亲节点,这是因为 5 出现在了 x 与 x 在栈中的下一个节点的反向中序遍历之间 ,因此 5 就是 x 的左儿子。
回到我们的例子,我们会依次从栈顶弹出 4,8 和 7,并且将 index 向左移动了三次。我们将 5 作为最后弹出的节点 7 的左儿子,并将 5 入栈。
stack = [3, 20, 5]index -> inorder[5] = 5
我们遍历 9。同理,index 恰好指向当前栈顶节点 5,那么我们会依次从栈顶弹出 5,20 和 3,并且将 index 向左移动了三次。我们将 9 作为最后弹出的节点 3 的左儿子,并将 9 入栈。
stack = [9]index -> inorder[2] = 10
我们遍历 10,将 10 作为栈顶节点 9 的右儿子,并将 10 入栈。
stack = [9, 10]index -> inorder[2] = 10
我们遍历 15。index 恰好指向当前栈顶节点 10,那么我们会依次从栈顶弹出 10 和 9,并且将 index 向左移动了两次。我们将 15 作为最后弹出的节点 9 的左儿子,并将 15 入栈。
stack = [15]index -> inorder[0] = 15
此时遍历结束,我们就构造出了正确的二叉树。
算法
我们归纳出上述例子中的算法流程:
最后得到的二叉树即为答案。
[sol2-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution { public TreeNode buildTree (int [] inorder, int [] postorder) { if (postorder == null || postorder.length == 0 ) { return null ; } TreeNode root = new TreeNode (postorder[postorder.length - 1 ]); Deque<TreeNode> stack = new LinkedList <TreeNode>(); stack.push(root); int inorderIndex = inorder.length - 1 ; for (int i = postorder.length - 2 ; i >= 0 ; i--) { int postorderVal = postorder[i]; TreeNode node = stack.peek(); if (node.val != inorder[inorderIndex]) { node.right = new TreeNode (postorderVal); stack.push(node.right); } else { while (!stack.isEmpty() && stack.peek().val == inorder[inorderIndex]) { node = stack.pop(); inorderIndex--; } node.left = new TreeNode (postorderVal); stack.push(node.left); } } return root; } }
[sol2-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class Solution {public : TreeNode* buildTree (vector<int >& inorder, vector<int >& postorder) { if (postorder.size () == 0 ) { return nullptr ; } auto root = new TreeNode (postorder[postorder.size () - 1 ]); auto s = stack <TreeNode*>(); s.push (root); int inorderIndex = inorder.size () - 1 ; for (int i = int (postorder.size ()) - 2 ; i >= 0 ; i--) { int postorderVal = postorder[i]; auto node = s.top (); if (node->val != inorder[inorderIndex]) { node->right = new TreeNode (postorderVal); s.push (node->right); } else { while (!s.empty () && s.top ()->val == inorder[inorderIndex]) { node = s.top (); s.pop (); inorderIndex--; } node->left = new TreeNode (postorderVal); s.push (node->left); } } return root; } };
[sol2-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 func buildTree (inorder []int , postorder []int ) if len (postorder) == 0 { return nil } root := &TreeNode{Val: postorder[len (postorder)-1 ]} stack := []*TreeNode{root} inorderIndex := len (inorder) - 1 for i := len (postorder) - 2 ; i >= 0 ; i-- { postorderVal := postorder[i] node := stack[len (stack)-1 ] if node.Val != inorder[inorderIndex] { node.Right = &TreeNode{Val: postorderVal} stack = append (stack, node.Right) } else { for len (stack) > 0 && stack[len (stack)-1 ].Val == inorder[inorderIndex] { node = stack[len (stack)-1 ] stack = stack[:len (stack)-1 ] inorderIndex-- } node.Left = &TreeNode{Val: postorderVal} stack = append (stack, node.Left) } } return root }
[sol2-JavaScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 var buildTree = function (inorder, postorder ) { if (postorder.length == 0 ) { return null ; } const root = new TreeNode (postorder[postorder.length - 1 ]); const stack = []; stack.push (root); let inorderIndex = inorder.length - 1 ; for (let i = postorder.length - 2 ; i >= 0 ; i--) { let postorderVal = postorder[i]; let node = stack[stack.length - 1 ]; if (node.val !== inorder[inorderIndex]) { node.right = new TreeNode (postorderVal); stack.push (node.right ); } else { while (stack.length && stack[stack.length - 1 ].val === inorder[inorderIndex]) { node = stack.pop (); inorderIndex--; } node.left = new TreeNode (postorderVal); stack.push (node.left ); } } return root; };
[sol2-C] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 struct TreeNode* createTreeNode (int val) { struct TreeNode * ret =malloc (sizeof (struct TreeNode)); ret->val = val; ret->left = ret->right = NULL ; return ret; } struct TreeNode* buildTree (int * inorder, int inorderSize, int * postorder, int postorderSize) { if (postorderSize == 0 ) { return NULL ; } struct TreeNode * root =1 ]); struct TreeNode ** s =malloc (sizeof (struct TreeNode*) * 10001 ); int top = 0 ; s[top++] = root; int inorderIndex = inorderSize - 1 ; for (int i = postorderSize - 2 ; i >= 0 ; i--) { int postorderVal = postorder[i]; struct TreeNode * node =1 ]; if (node->val != inorder[inorderIndex]) { node->right = createTreeNode(postorderVal); s[top++] = node->right; } else { while (top > 0 && s[top - 1 ]->val == inorder[inorderIndex]) { node = s[--top]; inorderIndex--; } node->left = createTreeNode(postorderVal); s[top++] = node->left; } } return root; }
复杂度分析

 {:width=480}
{:width=480} ,
, ,
, ,
, ,
, ,
, ,
, >
>