0122-买卖股票的最佳时机 II

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 10:42:36 2023-09-13 10:42:36 Updated    

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。

返回 你能获得的 最大 利润 。

示例 1：

**输入：** prices = [7,1,5,3,6,4]
**输出：** 7
**解释：** 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
     随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
     总利润为 4 + 3 = 7 。

示例 2：

**输入：** prices = [1,2,3,4,5]
**输出：** 4
**解释：** 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
     总利润为 4 。

示例 3：

**输入：** prices = [7,6,4,3,1]
**输出：** 0
**解释：** 在这种情况下, 交易无法获得正利润，所以不参与交易可以获得最大利润，最大利润为 0 。

提示：

  • 1 <= prices.length <= 3 * 104
  • 0 <= prices[i] <= 104

这一系列问题的目录：

题号 题解
121. 买卖股票的最佳时机 暴力解法、动态规划（Java）
122. 买卖股票的最佳时机 II 暴力搜索、贪心算法、动态规划（Java）
123. 买卖股票的最佳时机 III 动态规划（Java）
188. 买卖股票的最佳时机 IV 动态规划（「力扣」更新过用例，只有优化空间的版本可以 AC）
309. 最佳买卖股票时机含冷冻期 动态规划（Java）
714. 买卖股票的最佳时机含手续费 动态规划（Java）

方法一：暴力搜索（超时）

根据题意：由于不限制交易次数，在每一天，就可以根据当前是否持有股票选择相应的操作。「暴力搜索」在树形问题里也叫「回溯搜索」、「回溯法」。

首先画出树形图，然后编码。

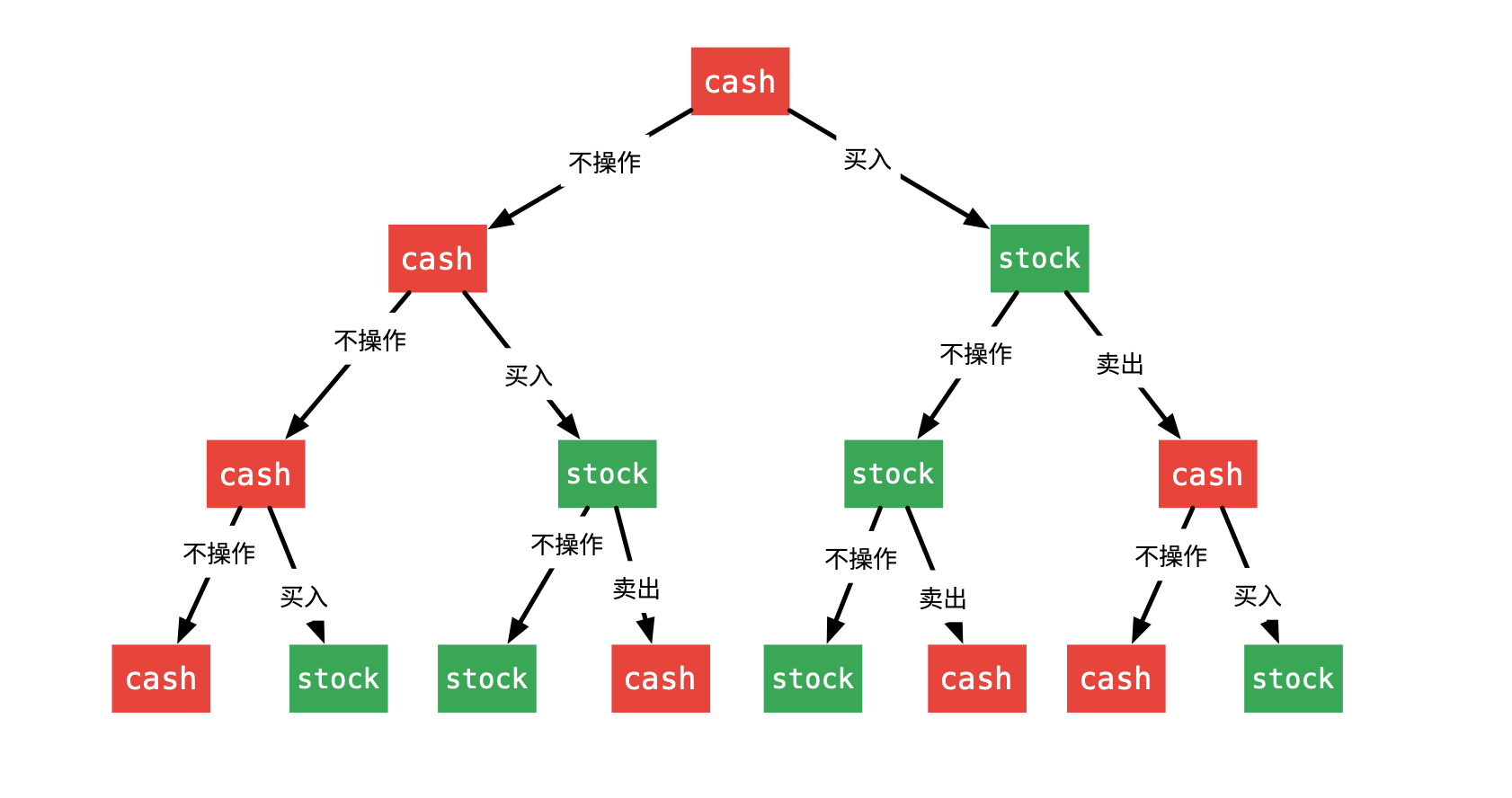image.png{:width=500}

参考代码 1：

[]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
public class Solution {

    private int res;

    public int maxProfit(int[] prices) {
        int len = prices.length;
        if (len < 2) {
            return 0;
        }
        this.res = 0;
        dfs(prices, 0, len, 0, res);
        return this.res;
    }

    /**
     * @param prices 股价数组
     * @param index  当前是第几天，从 0 开始
     * @param status 0 表示不持有股票，1表示持有股票，
     * @param profit 当前收益
     */
    private void dfs(int[] prices, int index, int len, int status, int profit) {

        if (index == len) {
            this.res = Math.max(this.res, profit);
            return;
        }

        dfs(prices, index + 1, len, status, profit);

        if (status == 0) {
            // 可以尝试转向 1
            dfs(prices, index + 1, len, 1, profit - prices[index]);

        } else {
            // 此时 status == 1，可以尝试转向 0
            dfs(prices, index + 1, len, 0, profit + prices[index]);
        }
    }
}

很显然，超时在意料之中。注意看这个超时是在数据规模很大的时候，因此，可以说明搜索算法是正确的。

image.png

image.png

方法二：动态规划（通用）

根据 「力扣」第 121 题的思路，需要设置一个二维矩阵表示状态。

第 1 步：定义状态

状态 dp[i][j] 定义如下：

dp[i][j] 表示到下标为 i 的这一天，持股状态为 j 时，我们手上拥有的最大现金数。

注意：限定持股状态为 j 是为了方便推导状态转移方程，这样的做法满足 无后效性。

其中：

  • 第一维 i 表示下标为 i 的那一天（ 具有前缀性质，即考虑了之前天数的交易 ）；
  • 第二维 j 表示下标为 i 的那一天是持有股票，还是持有现金。这里 0 表示持有现金（cash），1 表示持有股票（stock）。

第 2 步：思考状态转移方程

  • 状态从持有现金（cash）开始，到最后一天我们关心的状态依然是持有现金（cash）；
  • 每一天状态可以转移，也可以不动。状态转移用下图表示：

image.png{:width=500}

（状态转移方程写在代码中）

说明：

  • 由于不限制交易次数，除了最后一天，每一天的状态可能不变化，也可能转移；
  • 写代码的时候，可以不用对最后一天单独处理，输出最后一天，状态为 0 的时候的值即可。

第 3 步：确定初始值

起始的时候：

  • 如果什么都不做，dp[0][0] = 0；
  • 如果持有股票，当前拥有的现金数是当天股价的相反数，即 dp[0][1] = -prices[i]；

第 4 步：确定输出值

终止的时候，上面也分析了，输出 dp[len - 1][0]，因为一定有 dp[len - 1][0] > dp[len - 1][1]。

参考代码 2：

[]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public class Solution {

    public int maxProfit(int[] prices) {
        int len = prices.length;
        if (len < 2) {
            return 0;
        }

        // 0：持有现金
        // 1：持有股票
        // 状态转移：0 → 1 → 0 → 1 → 0 → 1 → 0
        int[][] dp = new int[len][2];

        dp[0][0] = 0;
        dp[0][1] = -prices[0];

        for (int i = 1; i < len; i++) {
            // 这两行调换顺序也是可以的
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
        }
        return dp[len - 1][0];
    }
}

复杂度分析：

  • 时间复杂度：$O(N)$，这里 $N$ 表示股价数组的长度；
  • 空间复杂度：$O(N)$，虽然是二维数组，但是第二维是常数，与问题规模无关。

我们也可以将状态数组分开设置。

参考代码 3：

[]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public class Solution {

    public int maxProfit(int[] prices) {
        int len = prices.length;
        if (len < 2) {
            return 0;
        }

        // cash：持有现金
        // hold：持有股票
        // 状态数组
        // 状态转移：cash → hold → cash → hold → cash → hold → cash
        int[] cash = new int[len];
        int[] hold = new int[len];

        cash[0] = 0;
        hold[0] = -prices[0];

        for (int i = 1; i < len; i++) {
            // 这两行调换顺序也是可以的
            cash[i] = Math.max(cash[i - 1], hold[i - 1] + prices[i]);
            hold[i] = Math.max(hold[i - 1], cash[i - 1] - prices[i]);
        }
        return cash[len - 1];
    }
}

复杂度分析：（同上）

第 5 步：考虑优化空间

由于当前行只参考上一行，每一行就 2 个值，因此可以考虑使用「滚动变量」（「滚动数组」技巧）。

参考代码 4：

[]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public class Solution {

    public int maxProfit(int[] prices) {
        int len = prices.length;
        if (len < 2) {
            return 0;
        }

        // cash：持有现金
        // hold：持有股票
        // 状态转移：cash → hold → cash → hold → cash → hold → cash

        int cash = 0;
        int hold = -prices[0];

        int preCash = cash;
        int preHold = hold;
        for (int i = 1; i < len; i++) {
            cash = Math.max(preCash, preHold + prices[i]);
            hold = Math.max(preHold, preCash - prices[i]);

            preCash = cash;
            preHold = hold;
        }
        return cash;
    }
}

复杂度分析：

  • 时间复杂度：$O(N)$，这里 $N$ 表示股价数组的长度；
  • 空间复杂度：$O(1)$，分别使用两个滚动变量，将一维数组状态优化到常数大小。

方法三：贪心算法（针对这道问题的特殊解法）

贪心算法的直觉：由于不限制交易次数，只要今天股价比昨天高，就交易。

下面对这个算法进行几点说明：

  • 该算法仅可以用于计算，但 计算的过程并不是真正交易的过程，但可以用贪心算法计算题目要求的最大利润。下面说明等价性：以 [1, 2, 3, 4] 为例，这 4 天的股价依次上升，按照贪心算法，得到的最大利润是：
[]
1
2
res =  (prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])
    =  prices[3] - prices[0]

仔细观察上面的式子，按照贪心算法，在下标为 1、2、3 的这三天，我们做的操作应该是买进昨天的，卖出今天的，虽然这种操作题目并不允许，但是它等价于：在下标为 0 的那一天买入，在下标为 3 的那一天卖出。

  • 为什么叫「贪心算法」

回到贪心算法的定义：（下面是来自《算法导论（第三版）》第 16 章的叙述）

{:width=560}

贪心算法 在每一步总是做出在当前看来最好的选择。

  • 「贪心算法」 和 「动态规划」、「回溯搜索」 算法一样，完成一件事情，是 分步决策 的；
  • 「贪心算法」 在每一步总是做出在当前看来最好的选择，我是这样理解 「最好」 这两个字的意思：
    • 「最好」 的意思往往根据题目而来，可能是 「最小」，也可能是 「最大」；
    • 贪心算法和动态规划相比，它既不看前面（也就是说它不需要从前面的状态转移过来），也不看后面（无后效性，后面的选择不会对前面的选择有影响），因此贪心算法时间复杂度一般是线性的，空间复杂度是常数级别的；
  • 这道题 「贪心」 的地方在于，对于 「今天的股价 - 昨天的股价」，得到的结果有 3 种可能：① 正数，② $0$，③负数。贪心算法的决策是： 只加正数 。

参考代码 5：

[]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public class Solution {

    public int maxProfit(int[] prices) {
        int len = prices.length;
        if (len < 2) {
            return 0;
        }

        int res = 0;
        for (int i = 1; i < len; i++) {
            int diff = prices[i] - prices[i - 1];
            if (diff > 0) {
                res += diff;
            }
        }
        return res;
    }
}

复杂度分析：

  • 时间复杂度：$O(N)$，这里 $N$ 表示股价数组的长度；
  • 空间复杂度：$O(1)$。

等价写法：

参考代码 6：

[]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public class Solution {

    public int maxProfit(int[] prices) {
        int len = prices.length;
        if (len < 2) {
            return 0;
        }

        int res = 0;
        for (int i = 1; i < len; i++) {
            res += Math.max(prices[i] - prices[i - 1], 0);
        }
        return res;
    }
}

复杂度分析：（同上）

下面证明 「贪心算法」 的有效性。

贪心选择性质的证明：

借助 「差分」 这个概念，可以证明 「贪心算法」 的有效性。贪心算法是选择那些所有差分（严格）大于 0 的数，把它们相加即可。

使用反证法：

假设 「贪心算法」 得到的解并不是最优解，即我们还能够找到一个可行解比 「贪心算法」 得到的利润还多。差分数组中除了差分为正数的项以外，还有就是差分为 $0$ 的项与差分为负数的项。「贪心算法」 是所有差分为正数的项的和。有以下 $3$ 种情况：

  • 如果可行解在 「贪心算法」 的基础上，选择了差分为 $0$ 的项，得到的结果与「贪心算法」得到的结果一样，因此加上差分为 $0$ 的项不会比「贪心算法」得到的结果更好；
  • 如果可行解在 「贪心算法」 的基础上，选择了差分为负数的项，加上一个负数得到的结果一定比 「贪心算法」 得到的结果要少，加上差分为负数的项，一定比 「贪心算法」 得到的结果更少；
  • 如果可行解在 「贪心算法」 的基础上，去掉了任何一个差分为正数的项，同上，得到的结果一定比 「贪心算法」 得到的结果要小，因此，「贪心算法」 的所有组成项不能删去任何一个。

综上，除了 「贪心算法」 以外，找不到一个更优的解法，因此 「贪心算法」 就是最优解。（证完）

 Comments
On this page
0122-买卖股票的最佳时机 II
  1. 方法一：暴力搜索（超时）
  2. 方法二：动态规划（通用）
  3. 第 1 步：定义状态
  4. 第 2 步：思考状态转移方程
  5. 第 3 步：确定初始值
  6. 第 4 步：确定输出值
  7. 第 5 步：考虑优化空间
  8. 方法三：贪心算法（针对这道问题的特殊解法）