按字典 wordList 完成从单词 beginWord 到单词 endWord 转化,一个表示此过程的 转换序列 是形式上像
beginWord -> s1 -> s2 -> ... -> sk 这样的单词序列,并满足:
- 每对相邻的单词之间仅有单个字母不同。
- 转换过程中的每个单词
si(1 <= i <= k)必须是字典 wordList 中的单词。注意,beginWord 不必是字典 wordList 中的单词。
sk == endWord
给你两个单词 beginWord 和 endWord ,以及一个字典 wordList 。请你找出并返回所有从 beginWord 到
endWord 的 最短转换序列 ,如果不存在这样的转换序列,返回一个空列表。每个序列都应该以单词列表 __[beginWord, s1, s2, ..., sk] 的形式返回。
示例 1:
**输入:** beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
**输出:** [["hit","hot","dot","dog","cog"],["hit","hot","lot","log","cog"]]
**解释:** 存在 2 种最短的转换序列:
"hit" -> "hot" -> "dot" -> "dog" -> "cog"
"hit" -> "hot" -> "lot" -> "log" -> "cog"
示例 2:
**输入:** beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
**输出:** []
**解释:** endWord "cog" 不在字典 wordList 中,所以不存在符合要求的转换序列。
提示:
1 <= beginWord.length <= 5endWord.length == beginWord.length1 <= wordList.length <= 500wordList[i].length == beginWord.lengthbeginWord、endWord 和 wordList[i] 由小写英文字母组成beginWord != endWordwordList 中的所有单词 互不相同
方法一:广度优先搜索 + 回溯
思路
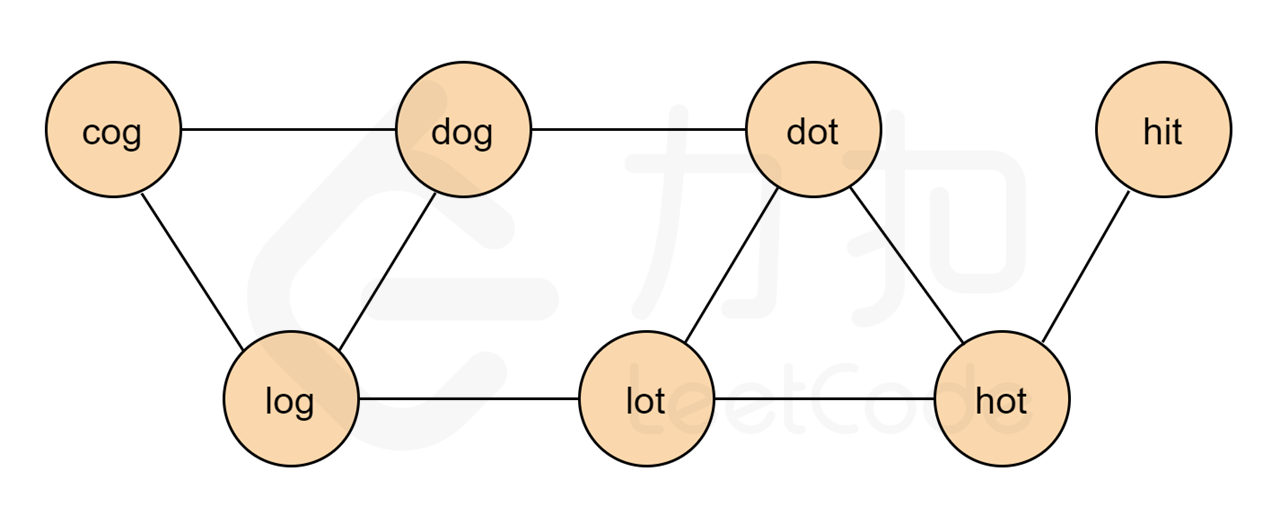
本题要求的是最短转换序列,看到最短首先想到的就是广度优先搜索。但是本题没有给出显示的图结构,根据单词转换规则:把每个单词都抽象为一个顶点,如果两个单词可以只改变一个字母进行转换,那么说明它们之间有一条双向边。因此我们只需要把满足转换条件的点相连,就形成了一张图。根据示例 1 中的输入,我们可以建出下图:
 {:width=”70%”}
{:width=”70%”}
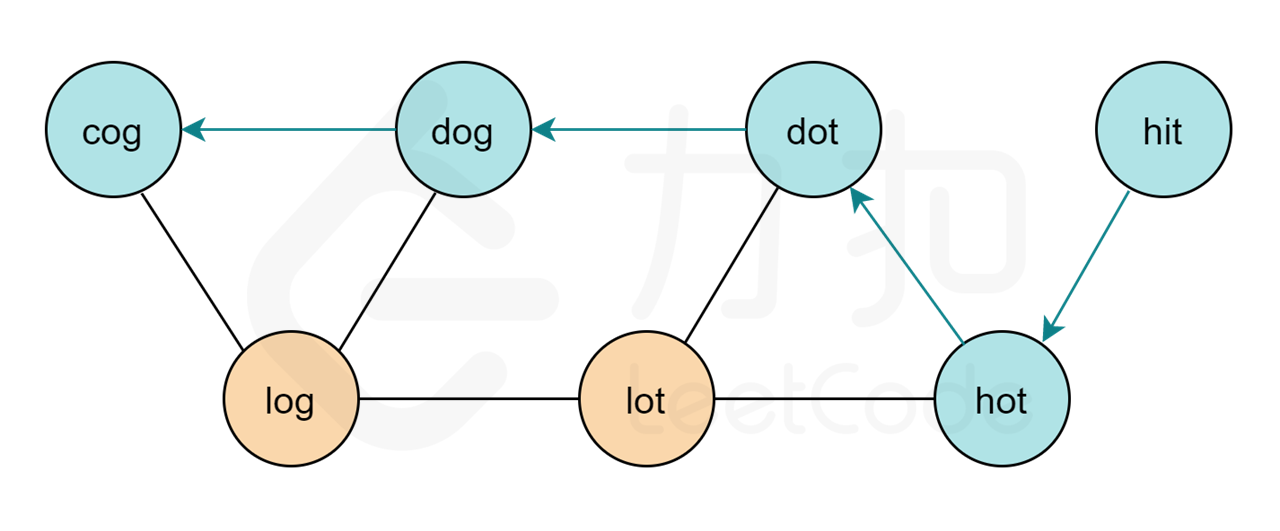
基于该图,我们以 $\text{hit"}$ 为图的起点, 以 $\text{cog”}$ 为终点进行广度优先搜索,寻找 $\text{hit"}$ 到 $\text{cog”}$ 的最短路径。下图即为答案中的一条路径。
 {:width=”70%”}
{:width=”70%”}
由于要求输出所有的最短路径,因此我们需要记录遍历路径,然后通过回溯得到所有的最短路径。
细节
- 从一个单词出发,修改每一位字符,将它修改成为 $\text{
a'}$ 到 $\text{z’}$ 中的所有字符,看看修改以后是不是在题目中给出的单词列表中;
- 有一些边的关系,由于不是最短路径上的边,不可以被记录下来。为此,我们为扩展出的单词记录附加的属性:层数。即下面代码中的 $\textit{steps}$。如果当前的单词扩散出去得到的单词的层数在以前出现过,则不应该记录这样的边的关系。
其它细节我们放在「代码」中,细节的部分比较多,读者朋友们需要仔细调试,相信掌握这道题对于大家来说会是一个很不错的编程练习。
代码
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
| class Solution {
public:
vector<vector<string>> findLadders(string beginWord, string endWord, vector<string> &wordList) {
vector<vector<string>> res;
unordered_set<string> dict = {wordList.begin(), wordList.end()};
if (dict.find(endWord) == dict.end()) {
return res;
}
dict.erase(beginWord);
unordered_map<string, int> steps = {{beginWord, 0}};
unordered_map<string, set<string>> from = {{beginWord, {}}};
int step = 0;
bool found = false;
queue<string> q = queue<string>{{beginWord}};
int wordLen = beginWord.length();
while (!q.empty()) {
step++;
int size = q.size();
for (int i = 0; i < size; i++) {
const string currWord = move(q.front());
string nextWord = currWord;
q.pop();
for (int j = 0; j < wordLen; ++j) {
const char origin = nextWord[j];
for (char c = 'a'; c <= 'z'; ++c) {
nextWord[j] = c;
if (steps[nextWord] == step) {
from[nextWord].insert(currWord);
}
if (dict.find(nextWord) == dict.end()) {
continue;
}
dict.erase(nextWord);
q.push(nextWord);
from[nextWord].insert(currWord);
steps[nextWord] = step;
if (nextWord == endWord) {
found = true;
}
}
nextWord[j] = origin;
}
}
if (found) {
break;
}
}
if (found) {
vector<string> Path = {endWord};
backtrack(res, endWord, from, Path);
}
return res;
}
void backtrack(vector<vector<string>> &res, const string &Node, unordered_map<string, set<string>> &from,
vector<string> &path) {
if (from[Node].empty()) {
res.push_back({path.rbegin(), path.rend()});
return;
}
for (const string &Parent: from[Node]) {
path.push_back(Parent);
backtrack(res, Parent, from, path);
path.pop_back();
}
}
};
|
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
| class Solution {
public List<List<String>> findLadders(String beginWord, String endWord, List<String> wordList) {
List<List<String>> res = new ArrayList<>();
Set<String> dict = new HashSet<>(wordList);
if (!dict.contains(endWord)) {
return res;
}
dict.remove(beginWord);
Map<String, Integer> steps = new HashMap<String, Integer>();
steps.put(beginWord, 0);
Map<String, List<String>> from = new HashMap<String, List<String>>();
int step = 1;
boolean found = false;
int wordLen = beginWord.length();
Queue<String> queue = new ArrayDeque<String>();
queue.offer(beginWord);
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
String currWord = queue.poll();
char[] charArray = currWord.toCharArray();
for (int j = 0; j < wordLen; j++) {
char origin = charArray[j];
for (char c = 'a'; c <= 'z'; c++) {
charArray[j] = c;
String nextWord = String.valueOf(charArray);
if (steps.containsKey(nextWord) && step == steps.get(nextWord)) {
from.get(nextWord).add(currWord);
}
if (!dict.contains(nextWord)) {
continue;
}
dict.remove(nextWord);
queue.offer(nextWord);
from.putIfAbsent(nextWord, new ArrayList<>());
from.get(nextWord).add(currWord);
steps.put(nextWord, step);
if (nextWord.equals(endWord)) {
found = true;
}
}
charArray[j] = origin;
}
}
step++;
if (found) {
break;
}
}
if (found) {
Deque<String> path = new ArrayDeque<>();
path.add(endWord);
backtrack(from, path, beginWord, endWord, res);
}
return res;
}
public void backtrack(Map<String, List<String>> from, Deque<String> path, String beginWord, String cur, List<List<String>> res) {
if (cur.equals(beginWord)) {
res.add(new ArrayList<>(path));
return;
}
for (String precursor : from.get(cur)) {
path.addFirst(precursor);
backtrack(from, path, beginWord, precursor, res);
path.removeFirst();
}
}
}
|
复杂度分析
(复杂度分析很复杂,我们面对算法面试、笔试不需要做严格的复杂度分析。)
拓展
由于本题起点和终点固定,所以可以从起点和终点同时开始进行双向广度优先搜索,可以进一步降低时间复杂度。