0129-求根节点到叶节点数字之和

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 10:42:44 2023-09-13 10:42:44 Updated    

给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。

每条从根节点到叶节点的路径都代表一个数字：

  • 例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。

计算从根节点到叶节点生成的 所有数字之和 。

叶节点 是指没有子节点的节点。

示例 1：

**输入：** root = [1,2,3]
**输出：** 25
**解释：**
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此，数字总和 = 12 + 13 = 25

示例 2：

**输入：** root = [4,9,0,5,1]
**输出：** 1026
**解释：**
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此，数字总和 = 495 + 491 + 40 = 1026

提示：

  • 树中节点的数目在范围 [1, 1000] 内
  • 0 <= Node.val <= 9
  • 树的深度不超过 10

前言

这道题中，二叉树的每条从根节点到叶子节点的路径都代表一个数字。其实，每个节点都对应一个数字，等于其父节点对应的数字乘以 $10$ 再加上该节点的值（这里假设根节点的父节点对应的数字是 $0$）。只要计算出每个叶子节点对应的数字，然后计算所有叶子节点对应的数字之和，即可得到结果。可以通过深度优先搜索和广度优先搜索实现。

方法一：深度优先搜索

思路与算法

深度优先搜索是很直观的做法。从根节点开始，遍历每个节点，如果遇到叶子节点，则将叶子节点对应的数字加到数字之和。如果当前节点不是叶子节点，则计算其子节点对应的数字，然后对子节点递归遍历。

fig1

代码

[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int sumNumbers(TreeNode root) {
        return dfs(root, 0);
    }

    public int dfs(TreeNode root, int prevSum) {
        if (root == null) {
            return 0;
        }
        int sum = prevSum * 10 + root.val;
        if (root.left == null && root.right == null) {
            return sum;
        } else {
            return dfs(root.left, sum) + dfs(root.right, sum);
        }
    }
}
[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int dfs(TreeNode* root, int prevSum) {
        if (root == nullptr) {
            return 0;
        }
        int sum = prevSum * 10 + root->val;
        if (root->left == nullptr && root->right == nullptr) {
            return sum;
        } else {
            return dfs(root->left, sum) + dfs(root->right, sum);
        }
    }
    int sumNumbers(TreeNode* root) {
        return dfs(root, 0);
    }
};
[sol1-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
const dfs = (root, prevSum) => {
    if (root === null) {
        return 0;
    }
    const sum = prevSum * 10 + root.val;
    if (root.left == null && root.right == null) {
        return sum;
    } else {
        return dfs(root.left, sum) + dfs(root.right, sum);
    }
}
var sumNumbers = function(root) {
    return dfs(root, 0);
};
[sol1-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int dfs(struct TreeNode* root, int prevSum) {
    if (root == NULL) {
        return 0;
    }
    int sum = prevSum * 10 + root->val;
    if (root->left == NULL && root->right == NULL) {
        return sum;
    } else {
        return dfs(root->left, sum) + dfs(root->right, sum);
    }
}

int sumNumbers(struct TreeNode* root) {
    return dfs(root, 0);
}
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def sumNumbers(self, root: TreeNode) -> int:
        def dfs(root: TreeNode, prevTotal: int) -> int:
            if not root:
                return 0
            total = prevTotal * 10 + root.val
            if not root.left and not root.right:
                return total
            else:
                return dfs(root.left, total) + dfs(root.right, total)

        return dfs(root, 0)
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
func dfs(root *TreeNode, prevSum int) int {
    if root == nil {
        return 0
    }
    sum := prevSum*10 + root.Val
    if root.Left == nil && root.Right == nil {
        return sum
    }
    return dfs(root.Left, sum) + dfs(root.Right, sum)
}

func sumNumbers(root *TreeNode) int {
    return dfs(root, 0)
}

复杂度分析

  • 时间复杂度：$O(n)$，其中 $n$ 是二叉树的节点个数。对每个节点访问一次。

  • 空间复杂度：$O(n)$，其中 $n$ 是二叉树的节点个数。空间复杂度主要取决于递归调用的栈空间，递归栈的深度等于二叉树的高度，最坏情况下，二叉树的高度等于节点个数，空间复杂度为 $O(n)$。

方法二：广度优先搜索

思路与算法

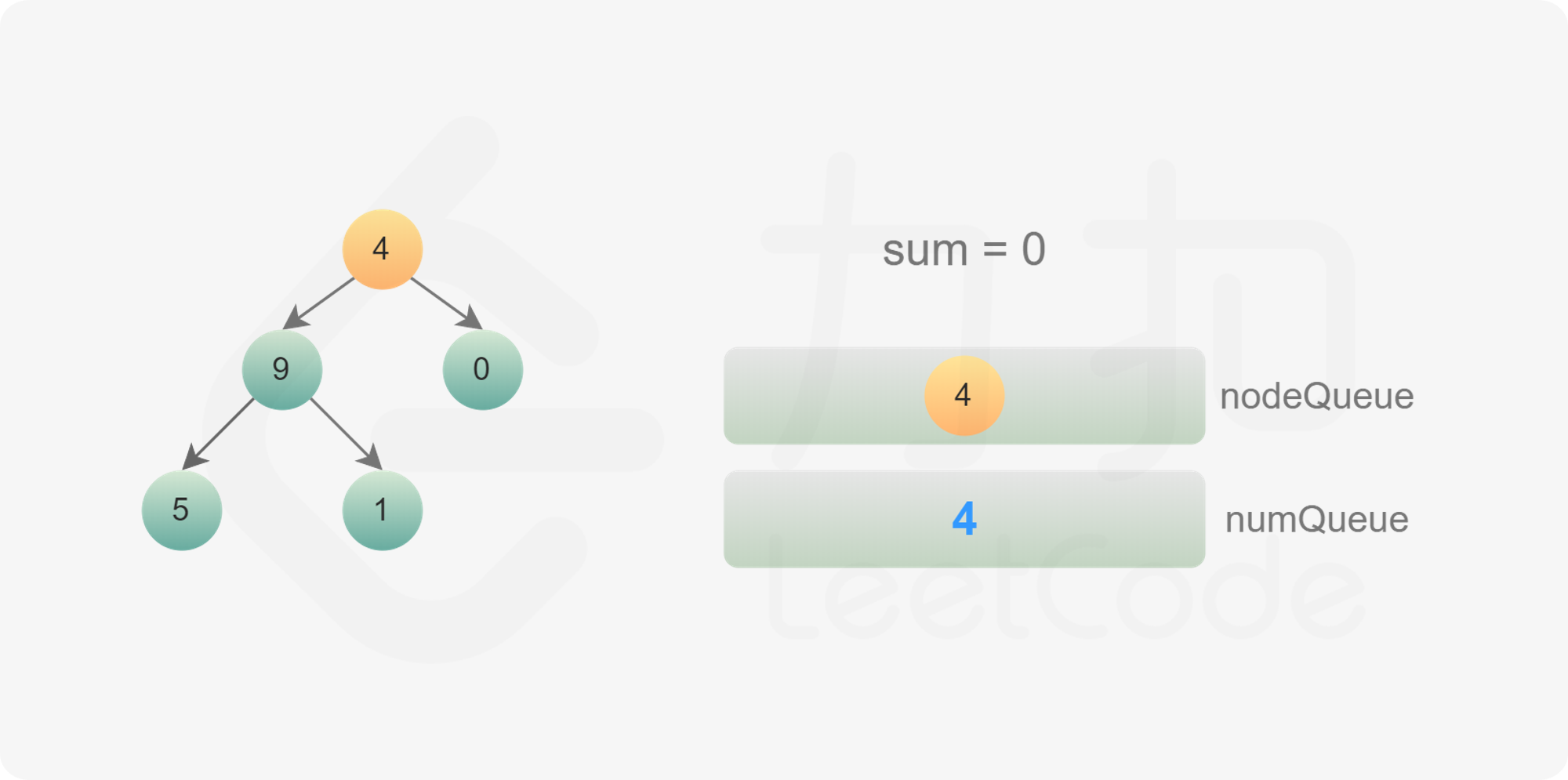
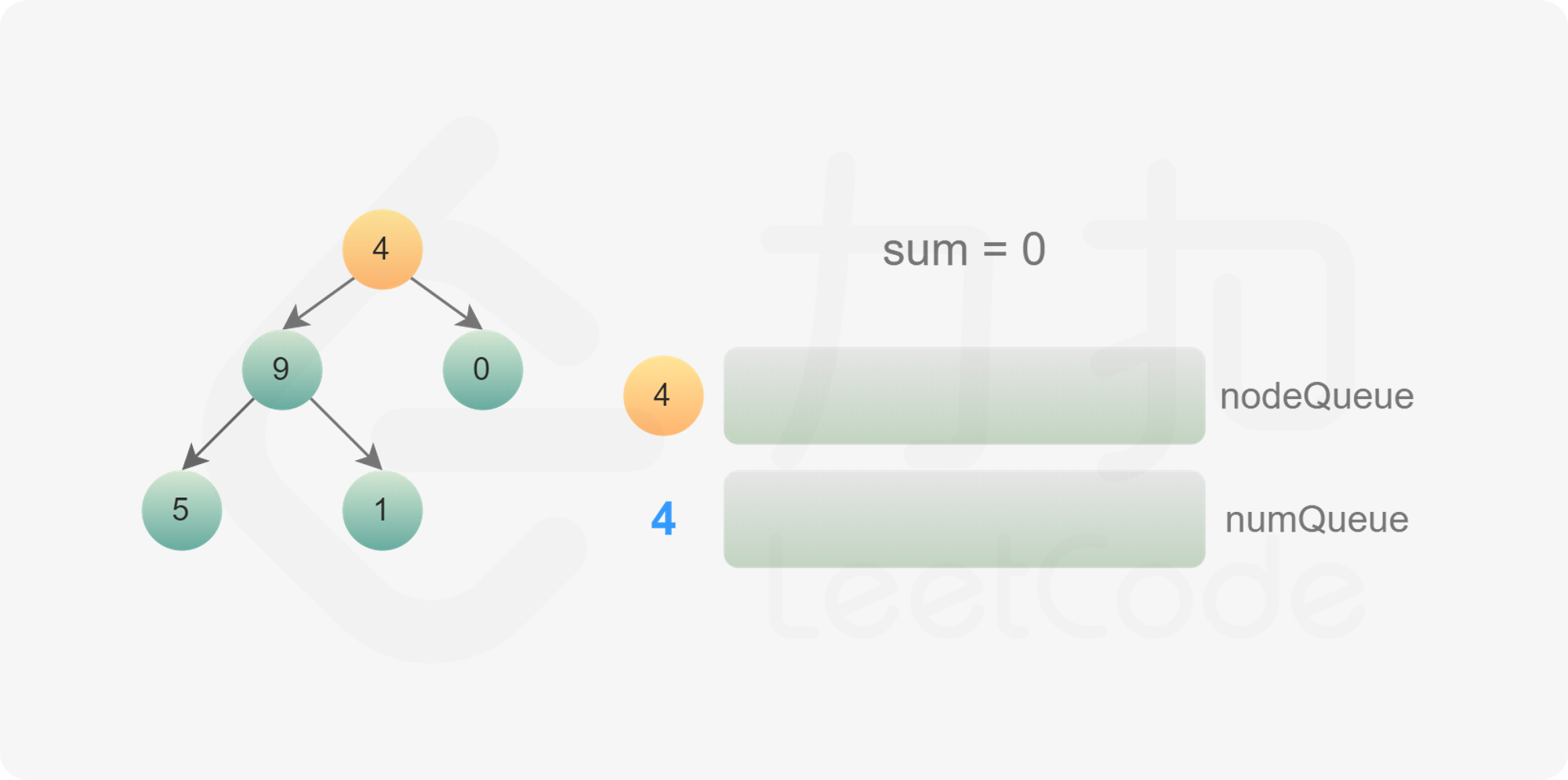
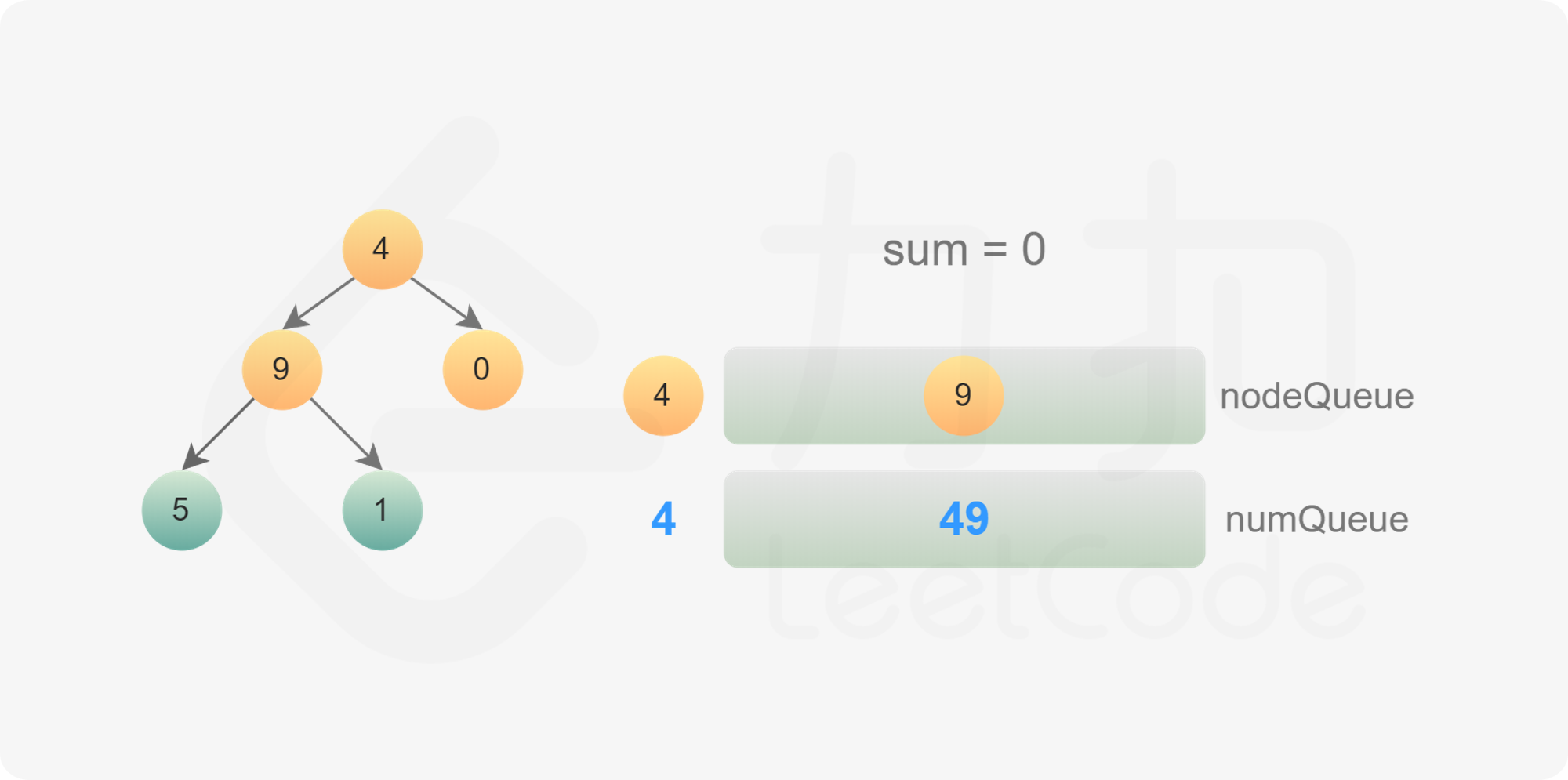
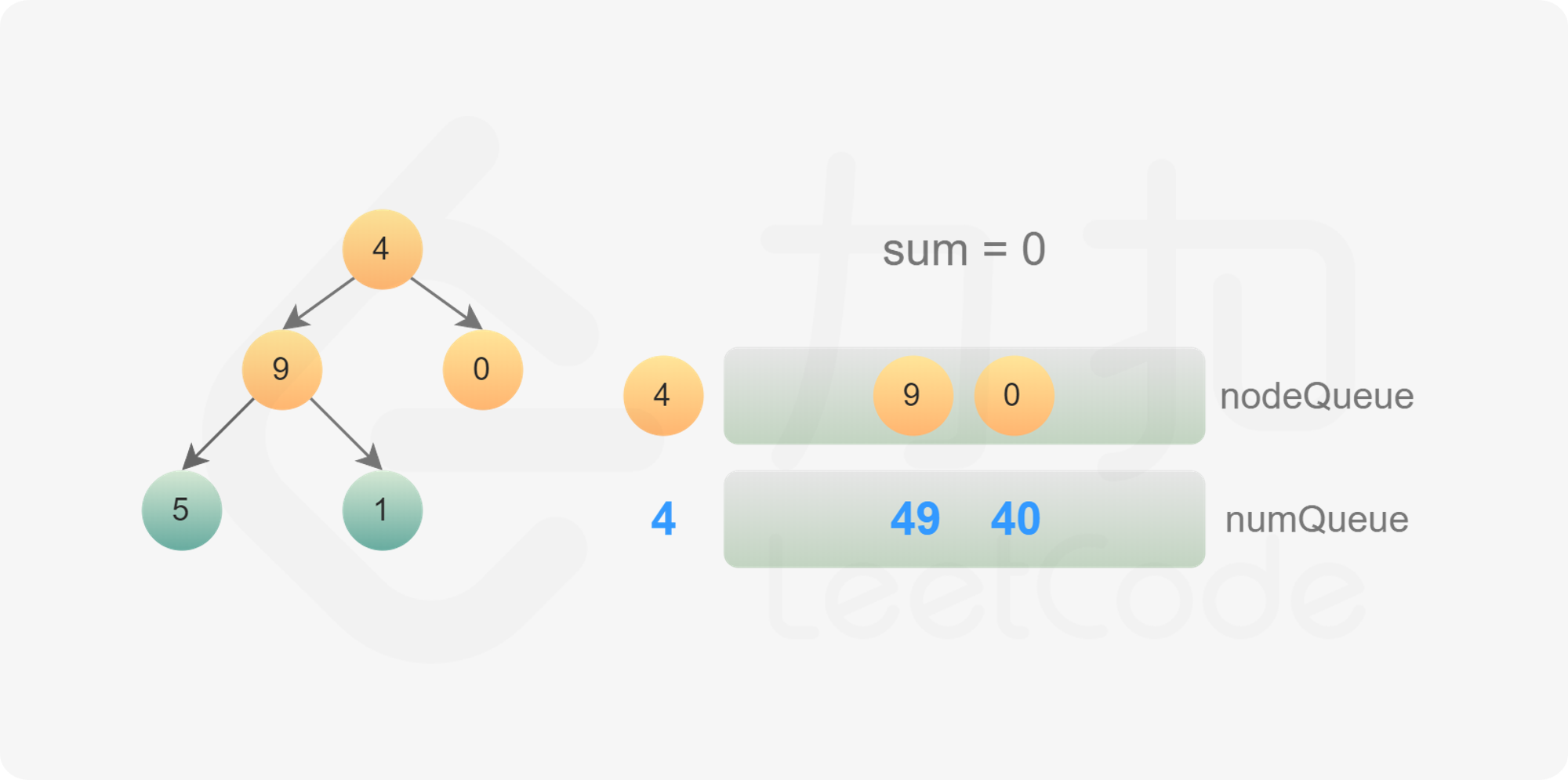
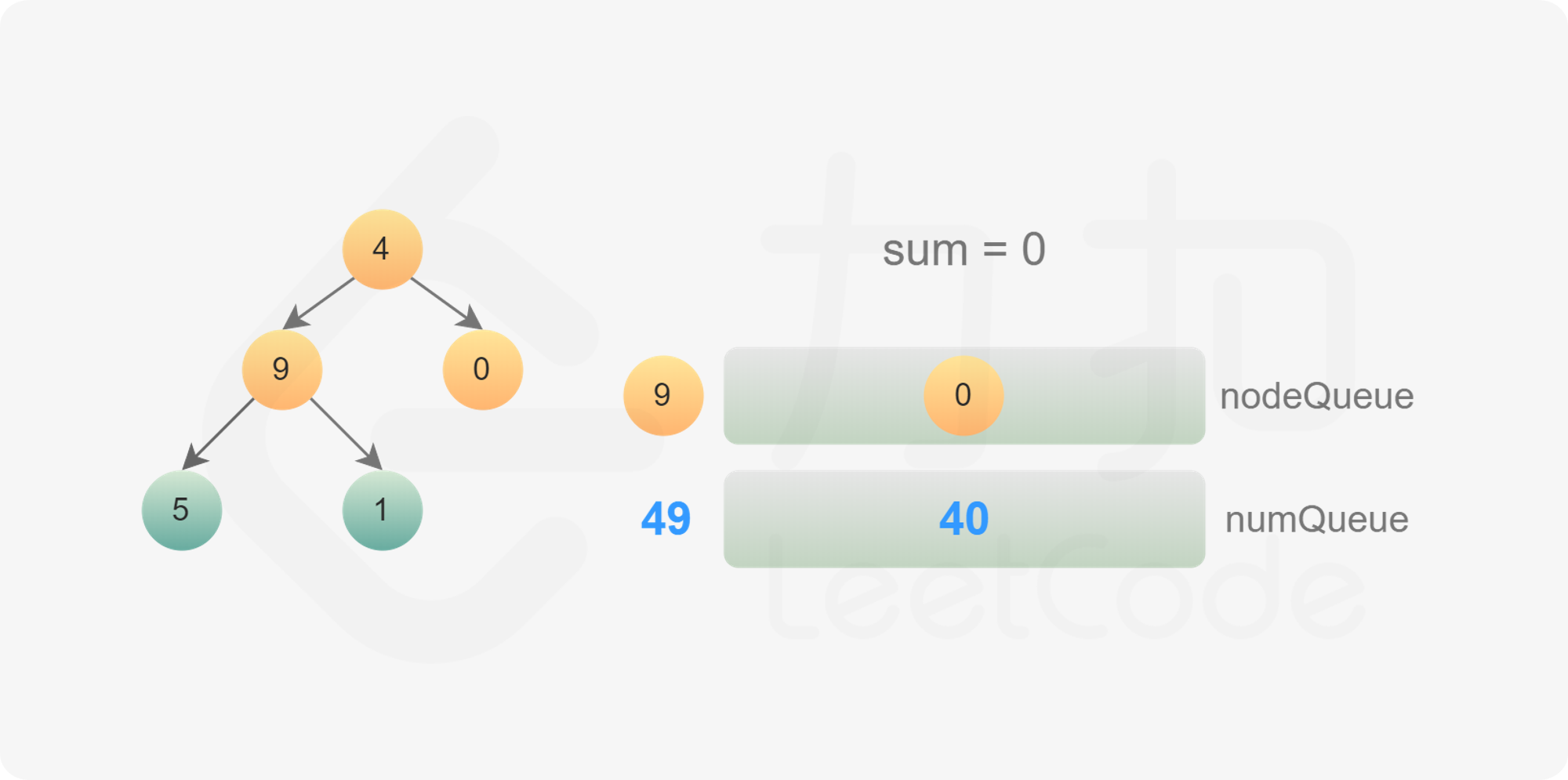
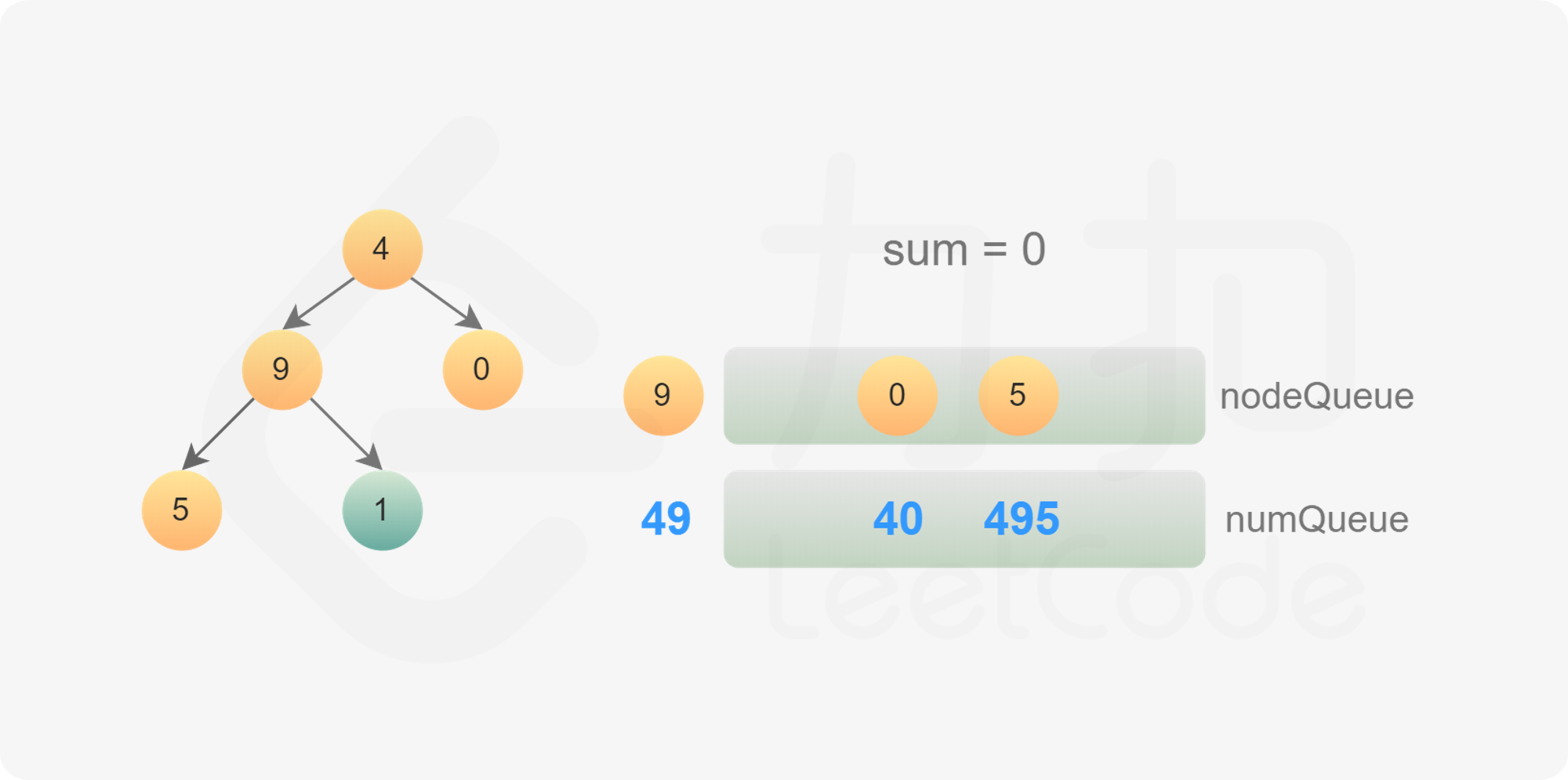
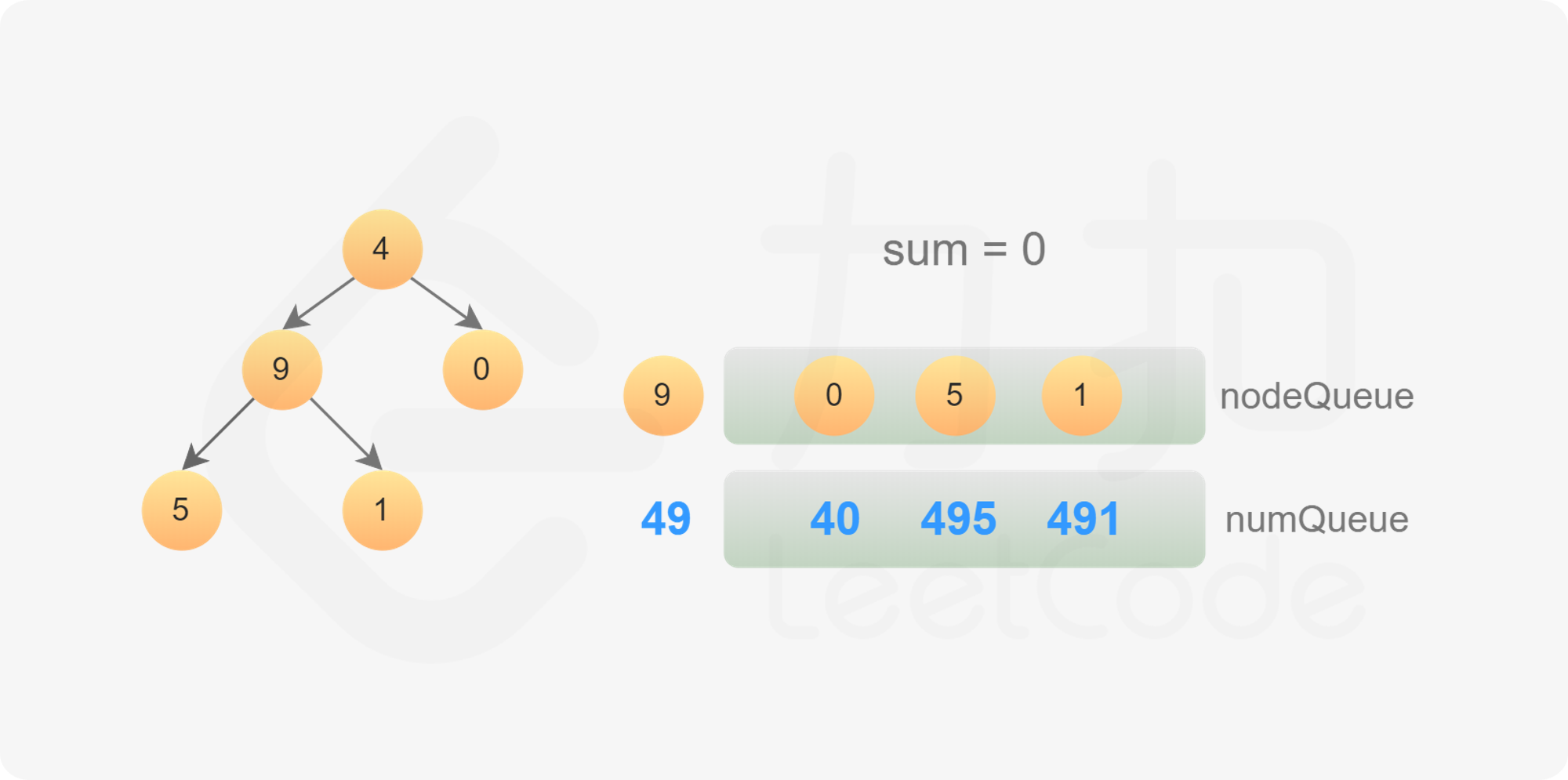
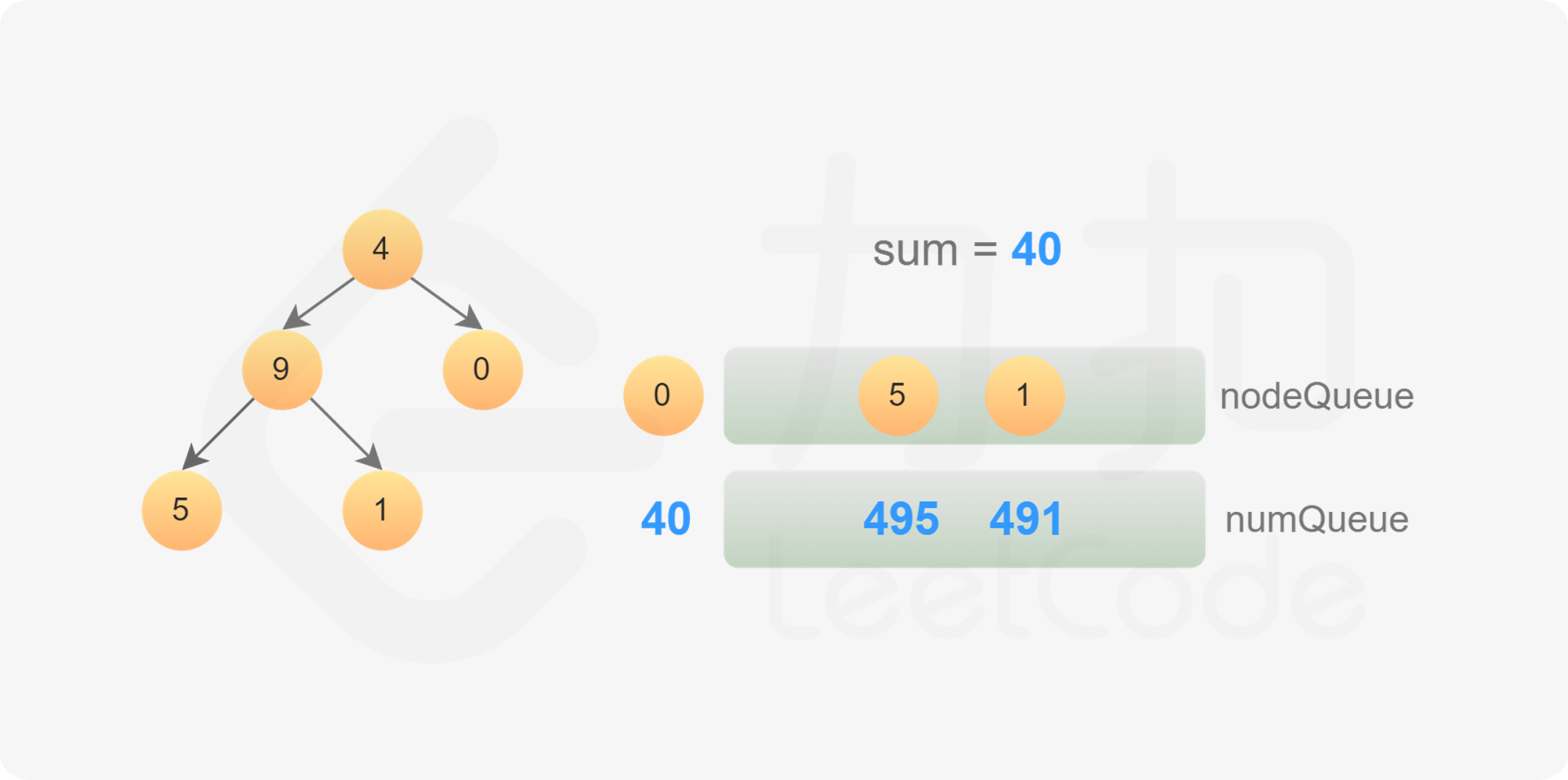
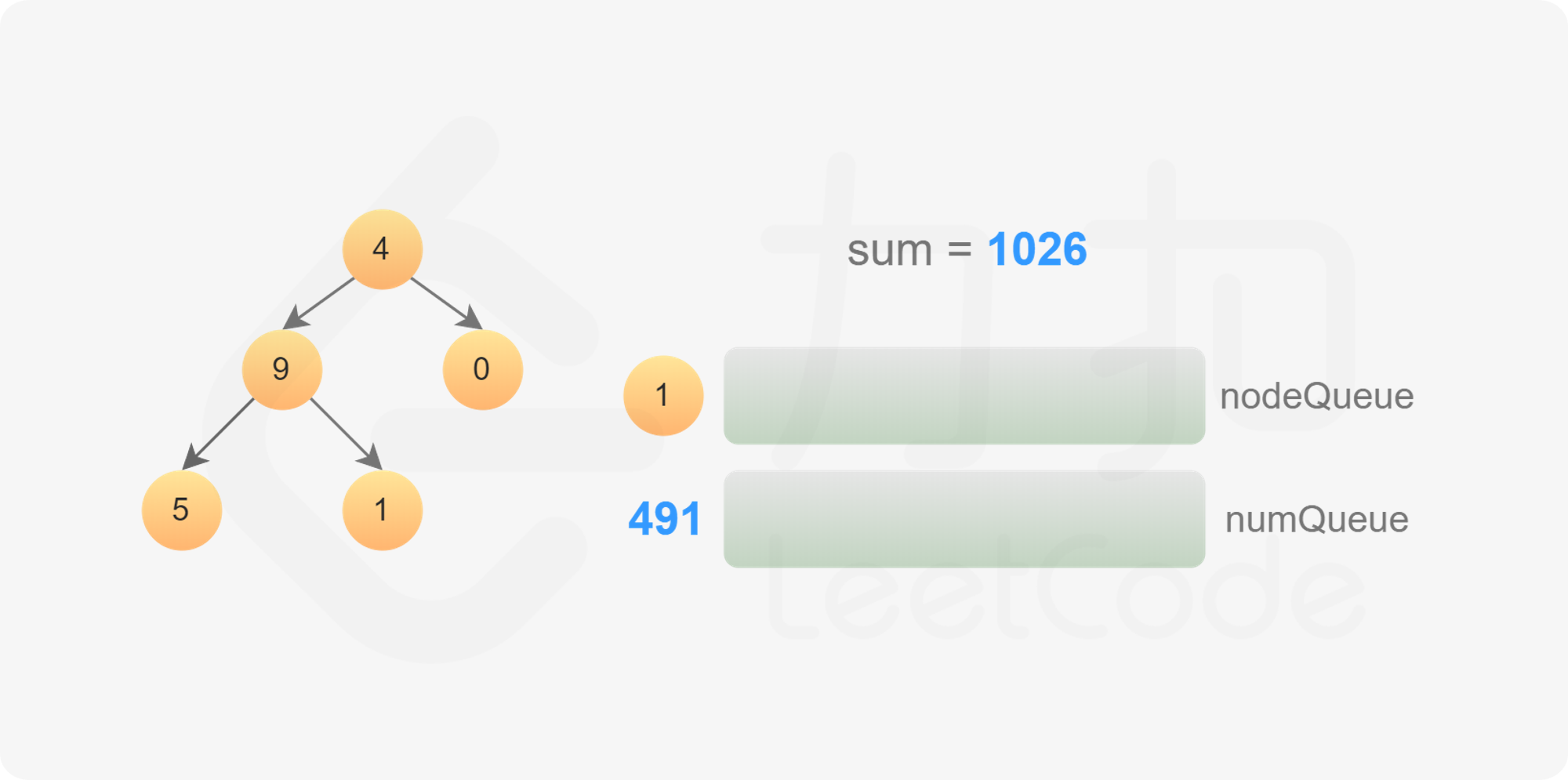
使用广度优先搜索，需要维护两个队列，分别存储节点和节点对应的数字。

初始时，将根节点和根节点的值分别加入两个队列。每次从两个队列分别取出一个节点和一个数字，进行如下操作：

  • 如果当前节点是叶子节点，则将该节点对应的数字加到数字之和；

  • 如果当前节点不是叶子节点，则获得当前节点的非空子节点，并根据当前节点对应的数字和子节点的值计算子节点对应的数字，然后将子节点和子节点对应的数字分别加入两个队列。

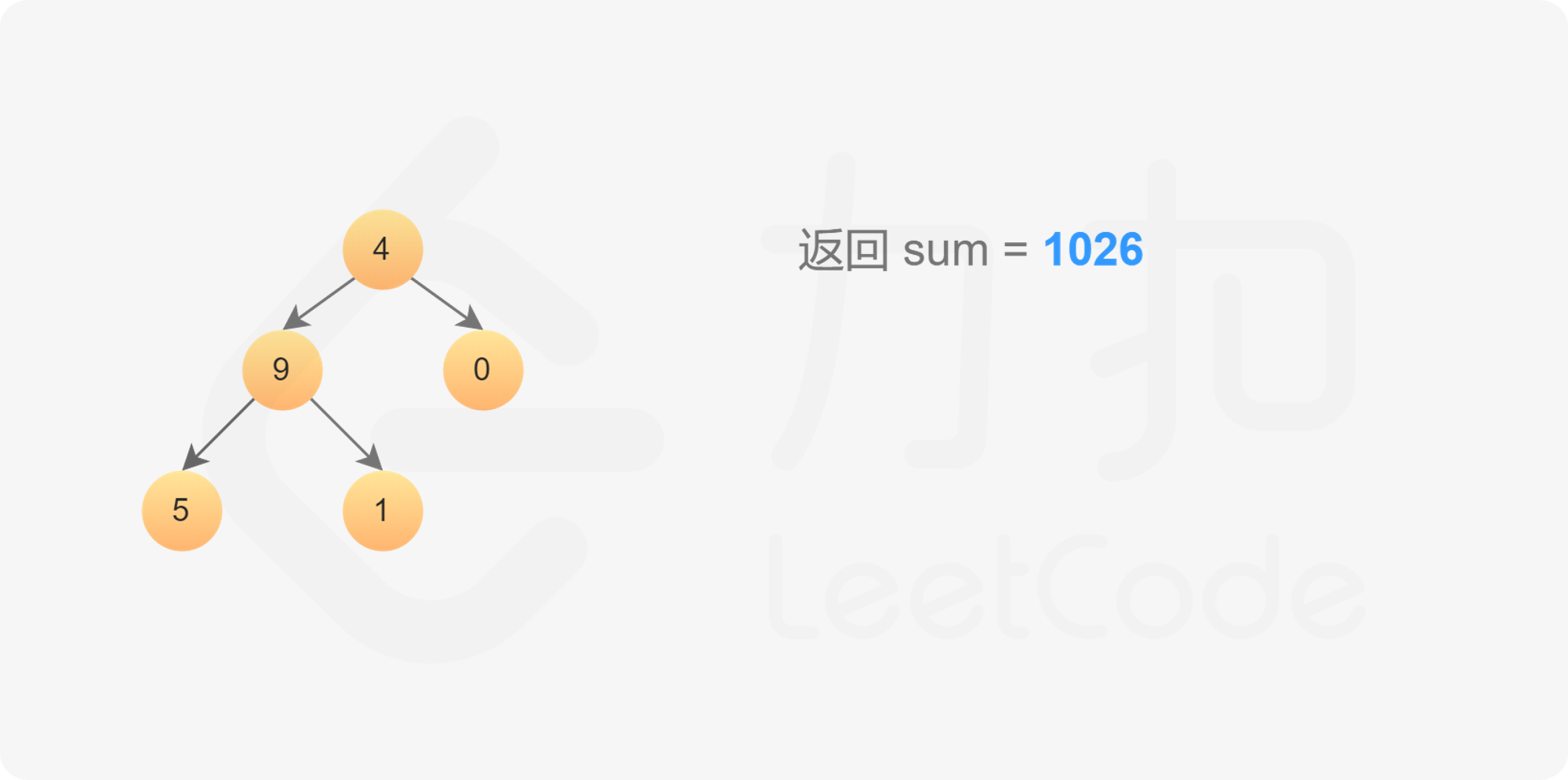
搜索结束后，即可得到所有叶子节点对应的数字之和。

<ppt1,ppt2,ppt3,ppt4,ppt5,ppt6,ppt7,ppt8,ppt9,ppt10,ppt11,ppt12>

代码

[sol2-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public int sumNumbers(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int sum = 0;
        Queue<TreeNode> nodeQueue = new LinkedList<TreeNode>();
        Queue<Integer> numQueue = new LinkedList<Integer>();
        nodeQueue.offer(root);
        numQueue.offer(root.val);
        while (!nodeQueue.isEmpty()) {
            TreeNode node = nodeQueue.poll();
            int num = numQueue.poll();
            TreeNode left = node.left, right = node.right;
            if (left == null && right == null) {
                sum += num;
            } else {
                if (left != null) {
                    nodeQueue.offer(left);
                    numQueue.offer(num * 10 + left.val);
                }
                if (right != null) {
                    nodeQueue.offer(right);
                    numQueue.offer(num * 10 + right.val);
                }
            }
        }
        return sum;
    }
}
[sol2-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    int sumNumbers(TreeNode* root) {
        if (root == nullptr) {
            return 0;
        }
        int sum = 0;
        queue<TreeNode*> nodeQueue;
        queue<int> numQueue;
        nodeQueue.push(root);
        numQueue.push(root->val);
        while (!nodeQueue.empty()) {
            TreeNode* node = nodeQueue.front();
            int num = numQueue.front();
            nodeQueue.pop();
            numQueue.pop();
            TreeNode* left = node->left;
            TreeNode* right = node->right;
            if (left == nullptr && right == nullptr) {
                sum += num;
            } else {
                if (left != nullptr) {
                    nodeQueue.push(left);
                    numQueue.push(num * 10 + left->val);
                }
                if (right != nullptr) {
                    nodeQueue.push(right);
                    numQueue.push(num * 10 + right->val);
                }
            }
        }
        return sum;
    }
};
[sol2-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
var sumNumbers = function(root) {
    if (root === null) {
        return 0;
    }
    let sum = 0;
    const nodeQueue = [];
    const numQueue = [];
    nodeQueue.push(root);
    numQueue.push(root.val);
    while (nodeQueue.length) {
        const node = nodeQueue.shift();
        const num = numQueue.shift();
        const left = node.left, right = node.right;
        if (left === null && right === null) {
            sum += num;
        } else {
            if (left !== null) {
                nodeQueue.push(left);
                numQueue.push(num * 10 + left.val);
            }
            if (right !== null) {
                nodeQueue.push(right);
                numQueue.push(num * 10 + right.val);
            }
        }
    }
    return sum;
};
[sol2-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
int sumNumbers(struct TreeNode* root) {
    if (root == NULL) {
        return 0;
    }
    int sum = 0;
    struct TreeNode* nodeQueue[2000];
    int numQueue[2000];
    int leftQueue = 0, rightQueue = 0;
    nodeQueue[rightQueue] = root;
    numQueue[rightQueue++] = root->val;
    while (leftQueue < rightQueue) {
        struct TreeNode* node = nodeQueue[leftQueue];
        int num = numQueue[leftQueue++];
        struct TreeNode* left = node->left;
        struct TreeNode* right = node->right;
        if (left == NULL && right == NULL) {
            sum += num;
        } else {
            if (left != NULL) {
                nodeQueue[rightQueue] = left;
                numQueue[rightQueue++] = num * 10 + left->val;
            }
            if (right != NULL) {
                nodeQueue[rightQueue] = right;
                numQueue[rightQueue++] = num * 10 + right->val;
            }
        }
    }
    return sum;
}
[sol2-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution:
    def sumNumbers(self, root: TreeNode) -> int:
        if not root:
            return 0

        total = 0
        nodeQueue = collections.deque([root])
        numQueue = collections.deque([root.val])
        
        while nodeQueue:
            node = nodeQueue.popleft()
            num = numQueue.popleft()
            left, right = node.left, node.right
            if not left and not right:
                total += num
            else:
                if left:
                    nodeQueue.append(left)
                    numQueue.append(num * 10 + left.val)
                if right:
                    nodeQueue.append(right)
                    numQueue.append(num * 10 + right.val)

        return total
[sol2-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
type pair struct {
    node *TreeNode
    num  int
}

func sumNumbers(root *TreeNode) (sum int) {
    if root == nil {
        return
    }
    queue := []pair{{root, root.Val}}
    for len(queue) > 0 {
        p := queue[0]
        queue = queue[1:]
        left, right, num := p.node.Left, p.node.Right, p.num
        if left == nil && right == nil {
            sum += num
        } else {
            if left != nil {
                queue = append(queue, pair{left, num*10 + left.Val})
            }
            if right != nil {
                queue = append(queue, pair{right, num*10 + right.Val})
            }
        }
    }
    return
}

复杂度分析

  • 时间复杂度：$O(n)$，其中 $n$ 是二叉树的节点个数。对每个节点访问一次。

  • 空间复杂度：$O(n)$，其中 $n$ 是二叉树的节点个数。空间复杂度主要取决于队列，每个队列中的元素个数不会超过 $n$。

 Comments
On this page
0129-求根节点到叶节点数字之和