0142-环形链表 II

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 10:43 2023-09-13 10:43 Updated    

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos
来表示链表尾连接到链表中的位置（ 索引从 0 开始 ）。如果 pos 是 -1，则在该链表中没有环。 注意：pos
不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例 1：

**输入：** head = [3,2,0,-4], pos = 1
**输出：** 返回索引为 1 的链表节点
**解释：** 链表中有一个环，其尾部连接到第二个节点。

示例 2：

![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2018/12/07/circularlinkedlist_test2.png)

**输入：** head = [1,2], pos = 0
**输出：** 返回索引为 0 的链表节点
**解释：** 链表中有一个环，其尾部连接到第一个节点。

示例 3：

![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2018/12/07/circularlinkedlist_test3.png)

**输入：** head = [1], pos = -1
**输出：** 返回 null
**解释：** 链表中没有环。

提示：

  • 链表中节点的数目范围在范围 [0, 104] 内
  • -105 <= Node.val <= 105
  • pos 的值为 -1 或者链表中的一个有效索引

进阶： 你是否可以使用 O(1) 空间解决此题？

解题思路：

这类链表题目一般都是使用双指针法解决的，例如寻找距离尾部第 K 个节点、寻找环入口、寻找公共尾部入口等。

在本题的求解过程中，双指针会产生两次“相遇”。

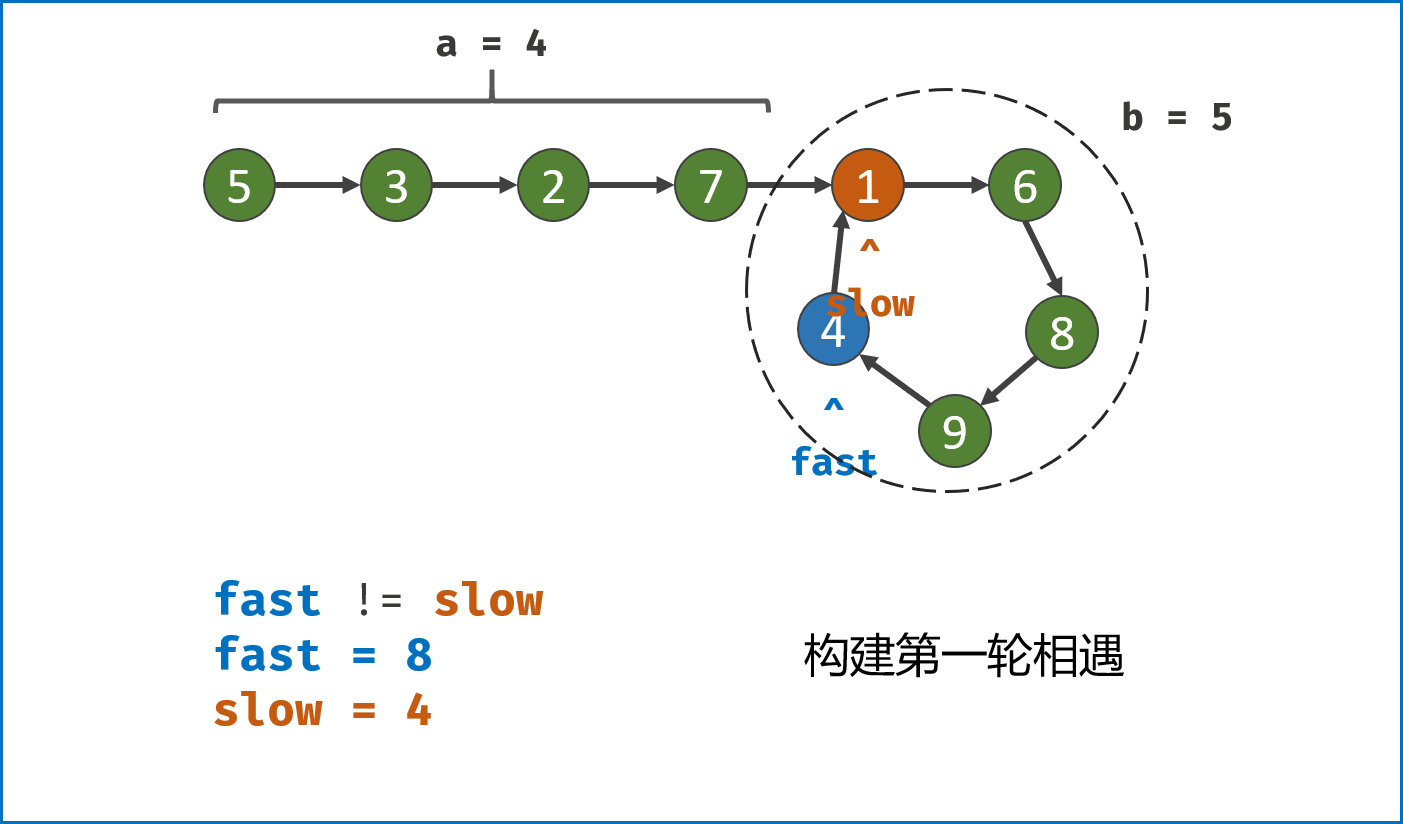
双指针的第一次相遇：

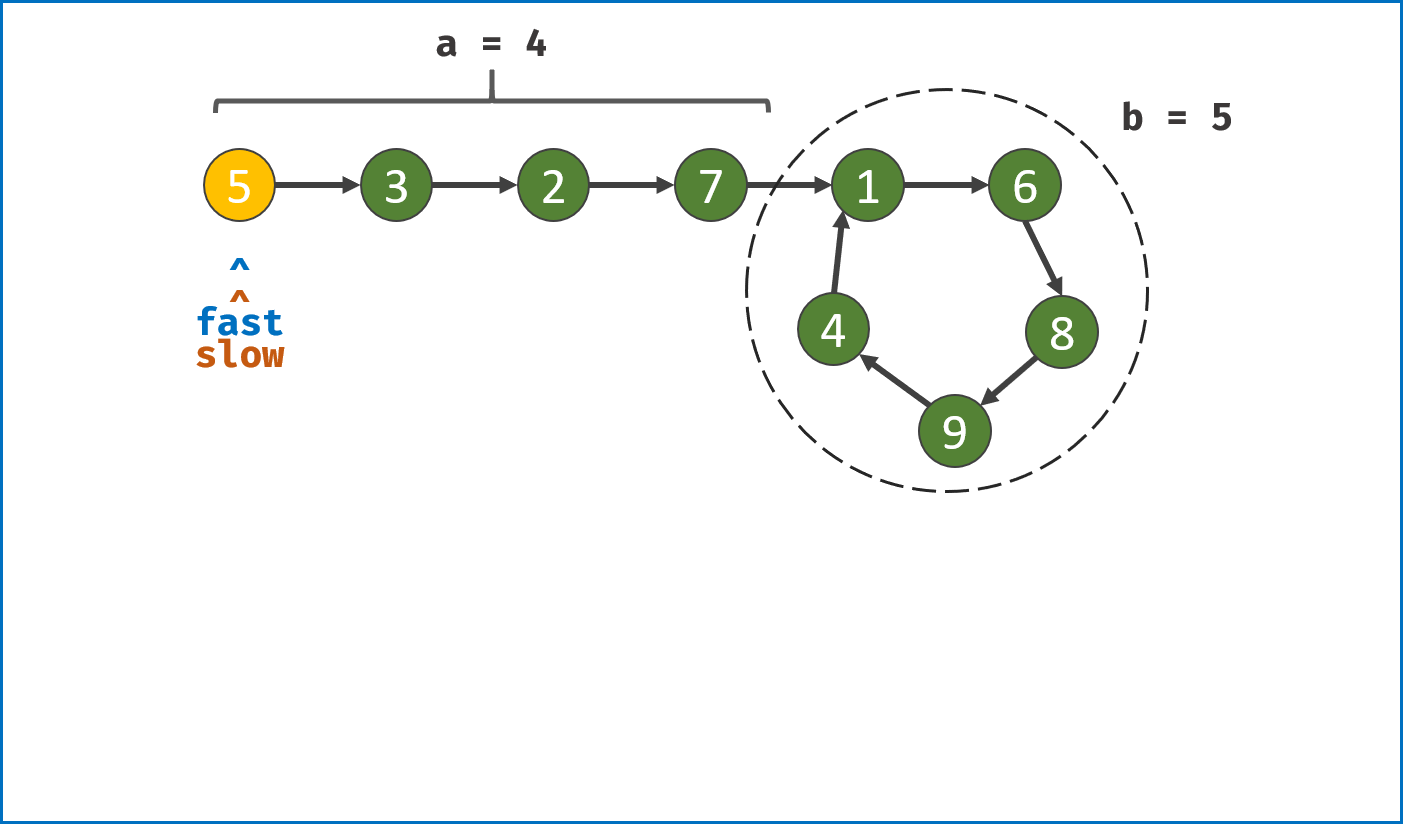
  1. 设两指针 fast，slow 指向链表头部 head 。
  2. 令 fast 每轮走 $2$ 步，slow 每轮走 $1$ 步。

执行以上两步后，可能出现两种结果：

第一种结果： fast 指针走过链表末端，说明链表无环，此时直接返回 null。

如果链表存在环，则双指针一定会相遇。因为每走 $1$ 轮，fast 与 slow 的间距 $+1$，fast 一定会追上 slow 。

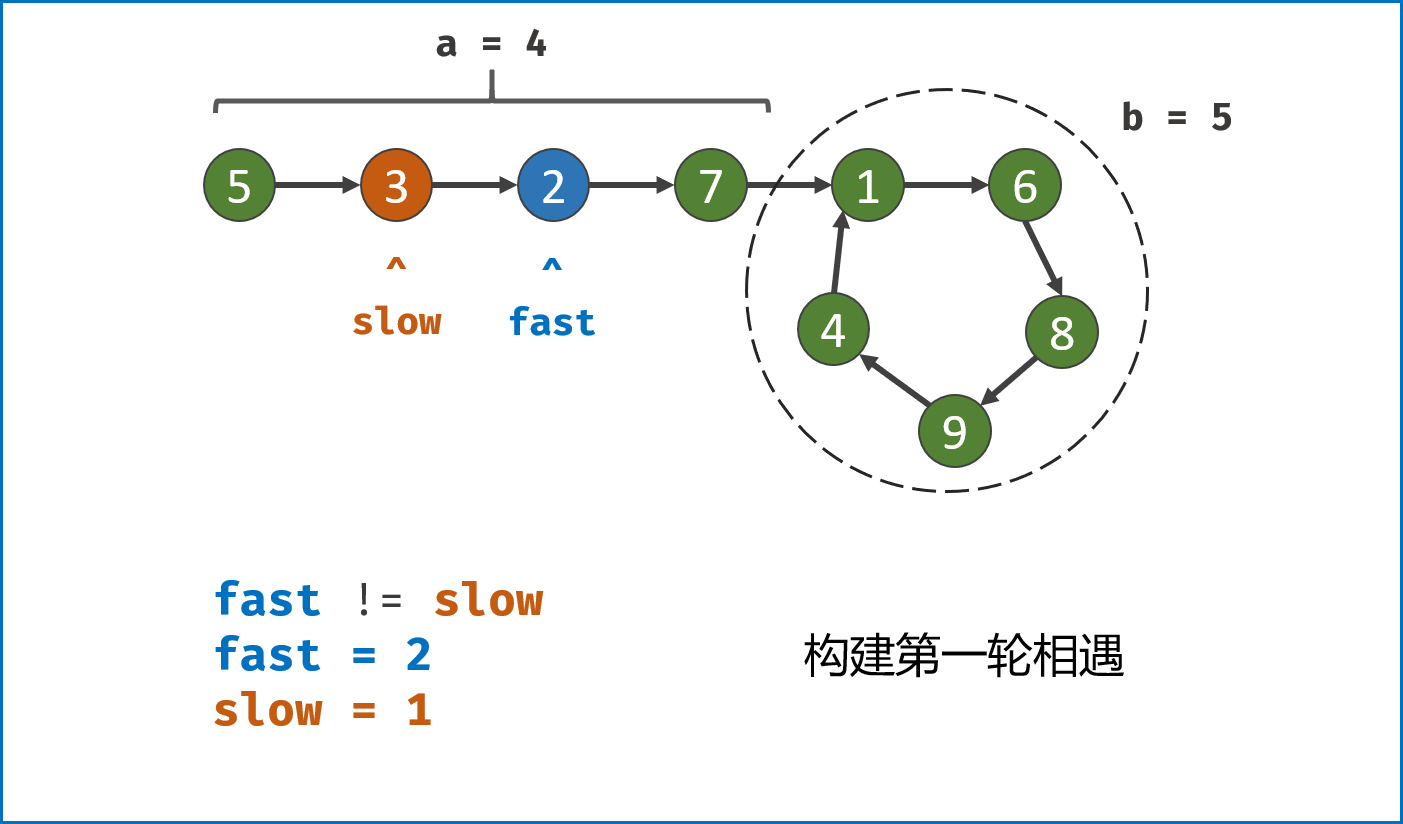
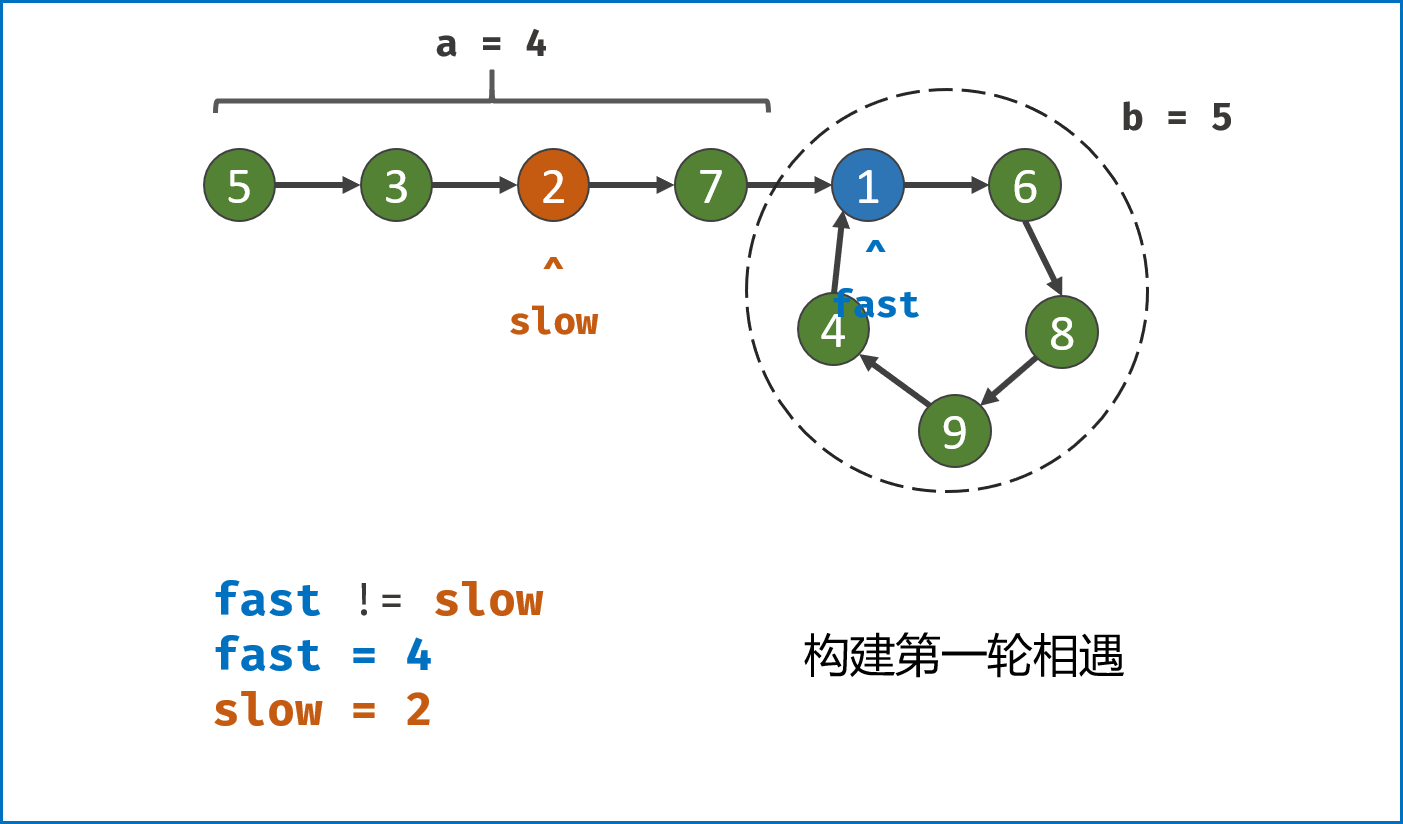
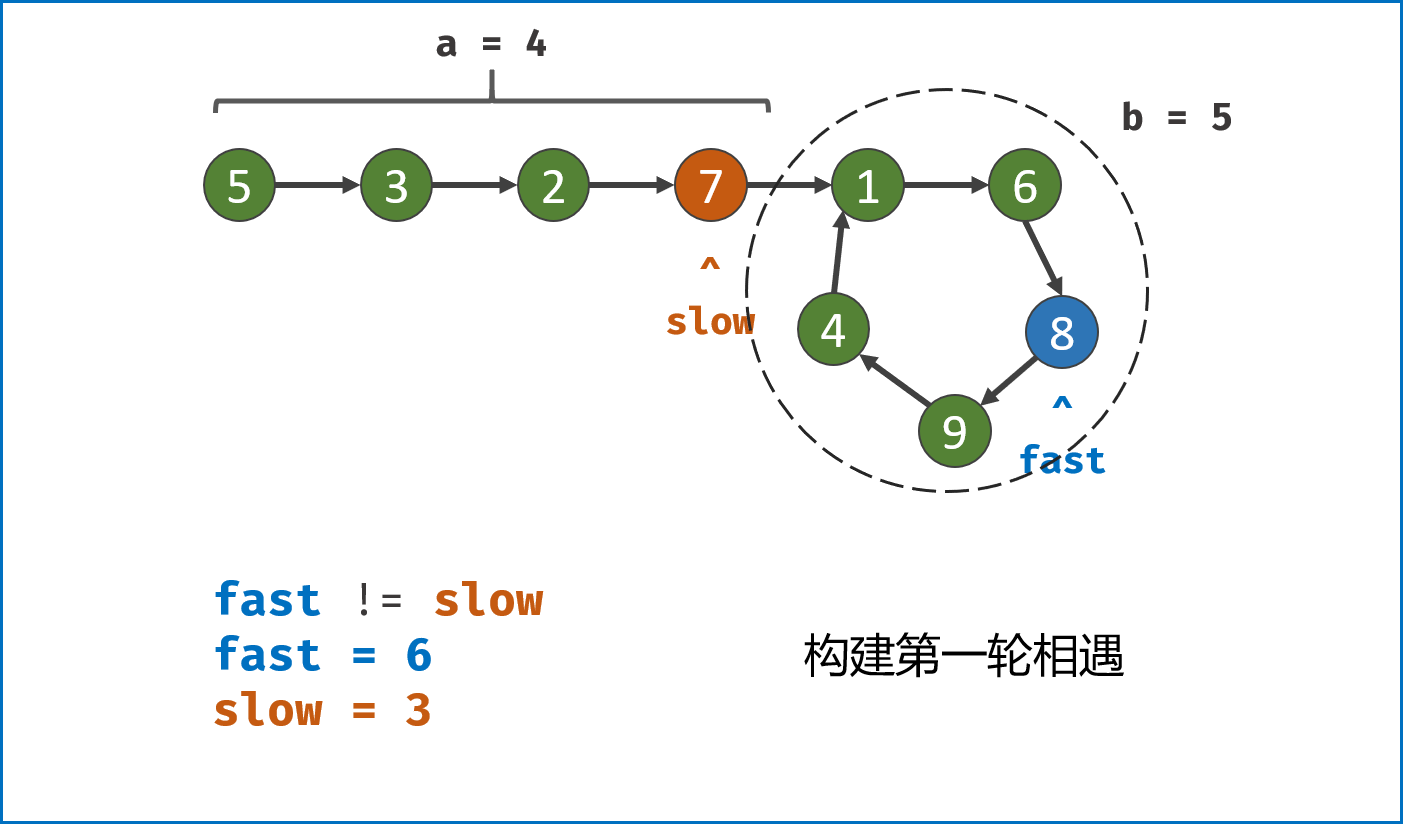
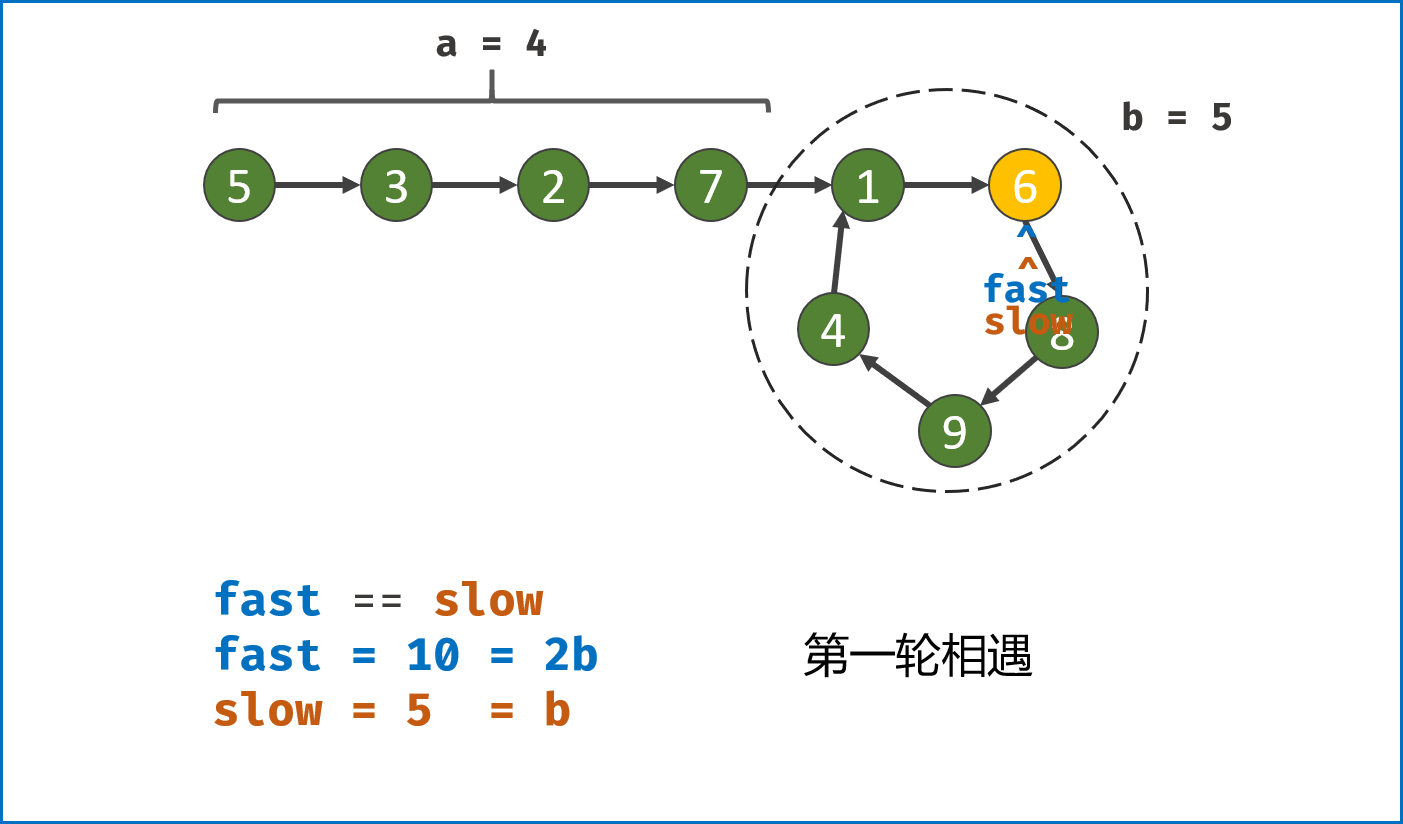
第二种结果： 当fast == slow时， 两指针在环中第一次相遇。下面分析此时 fast 与 slow 走过的步数关系：

设链表共有 $a+b$ 个节点，其中 链表头部到链表入口 有 $a$ 个节点（不计链表入口节点）， 链表环 有 $b$ 个节点（这里需要注意，$a$ 和 $b$ 是未知数，例如图解上链表 $a=4$ , $b=5$）；设两指针分别走了 $f$，$s$ 步，则有：

  1. fast 走的步数是 slow 步数的 $2$ 倍，即 $f = 2s$；（解析： fast 每轮走 $2$ 步）
  2. fast 比 slow 多走了 $n$ 个环的长度，即 $f = s + nb$；（ 解析： 双指针都走过 $a$ 步，然后在环内绕圈直到重合，重合时 fast 比 slow 多走 环的长度整数倍 ）。

将以上两式相减得到 $f = 2nb$，$s = nb$，即 fast 和 slow 指针分别走了 $2n$，$n$ 个环的周长。

接下来该怎么做呢？

如果让指针从链表头部一直向前走并统计步数k，那么所有 走到链表入口节点时的步数 是：$k=a+nb$ ，即先走 $a$ 步到入口节点，之后每绕 $1$ 圈环（ $b$ 步）都会再次到入口节点。而目前 slow 指针走了 $nb$ 步。因此，我们只要想办法让 slow 再走 $a$ 步停下来，就可以到环的入口。

但是我们不知道 $a$ 的值，该怎么办？依然是使用双指针法。考虑构建一个指针，此指针需要有以下性质：此指针和 slow 一起向前走 a 步后，两者在入口节点重合。那么从哪里走到入口节点需要 $a$ 步？答案是链表头节点head。

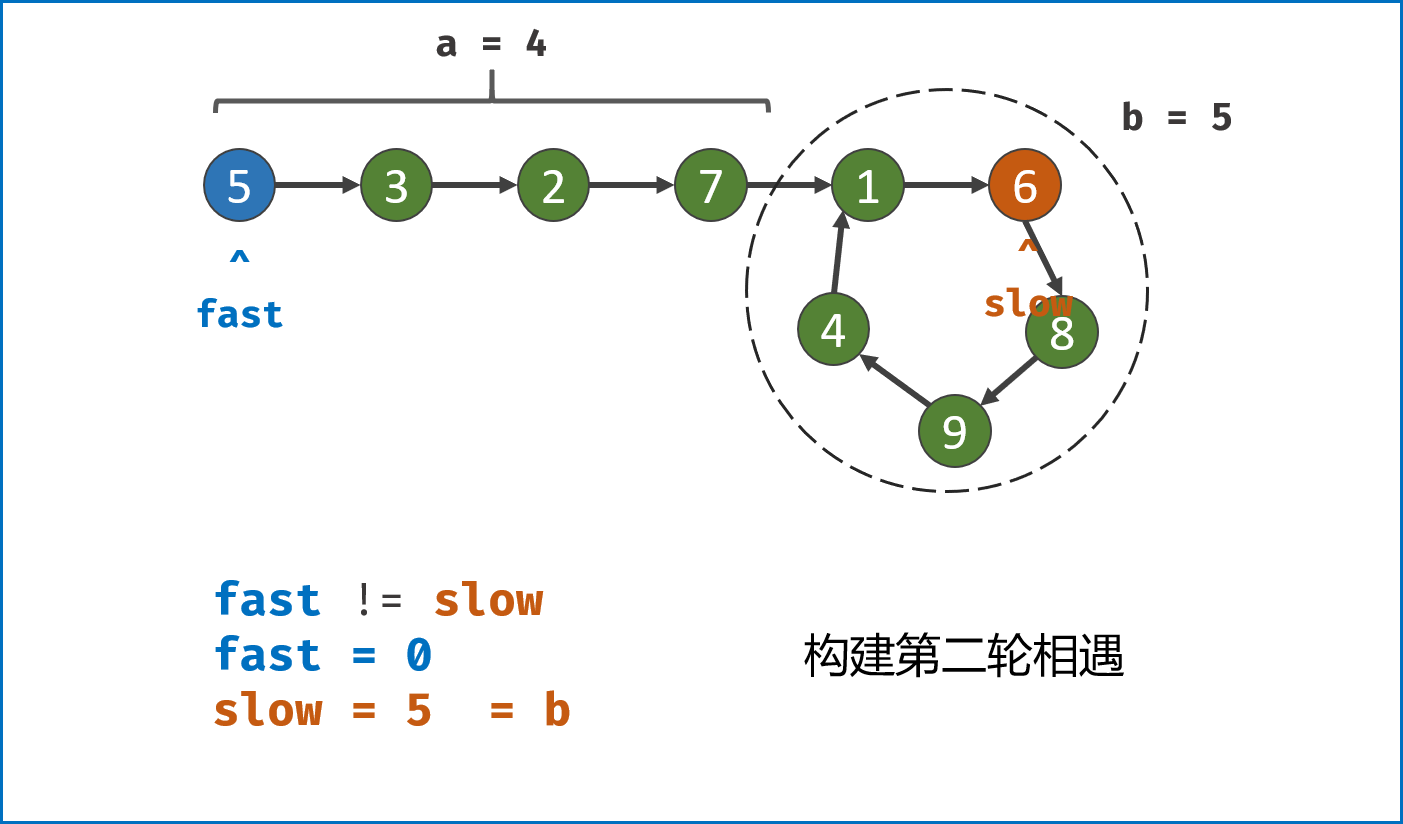
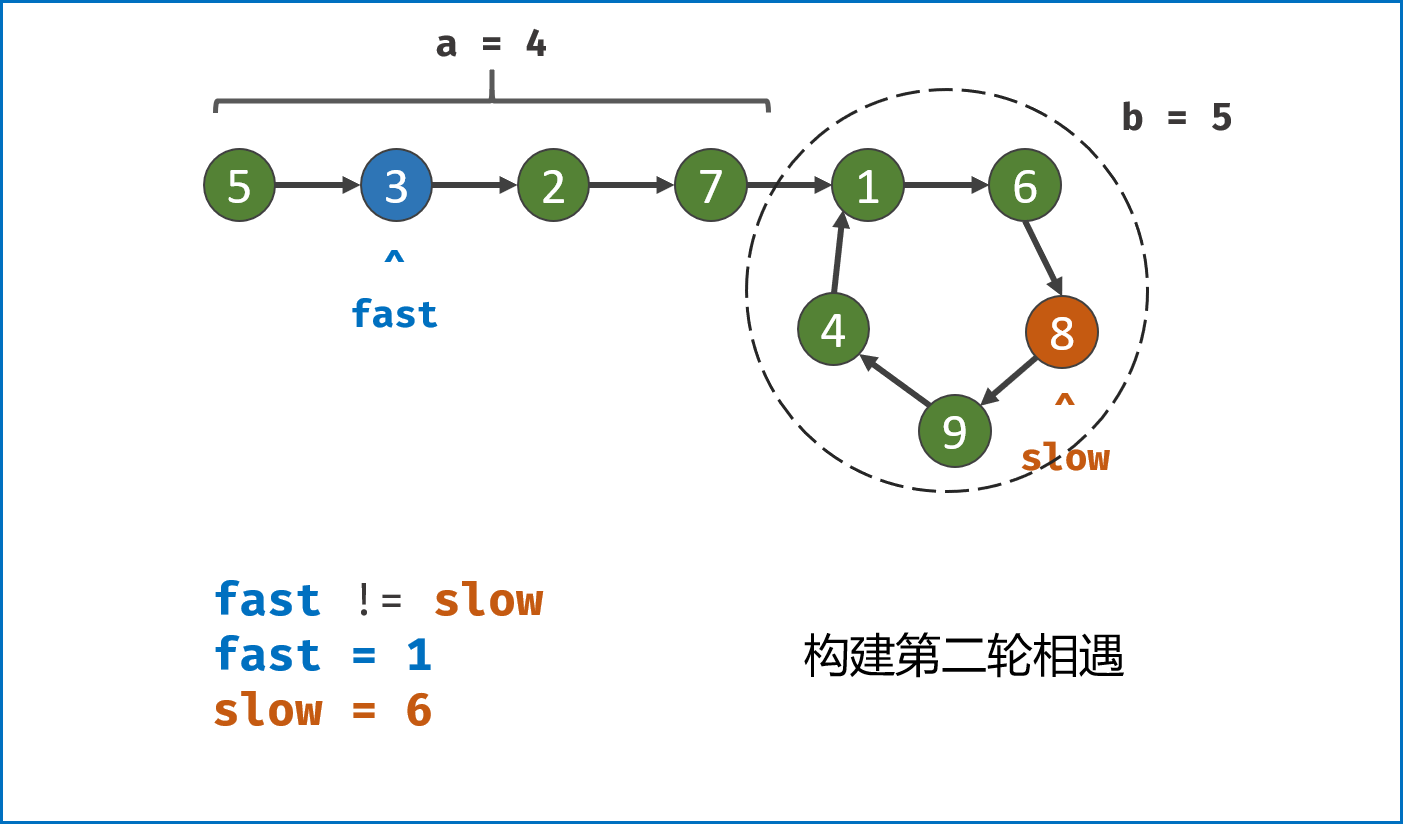
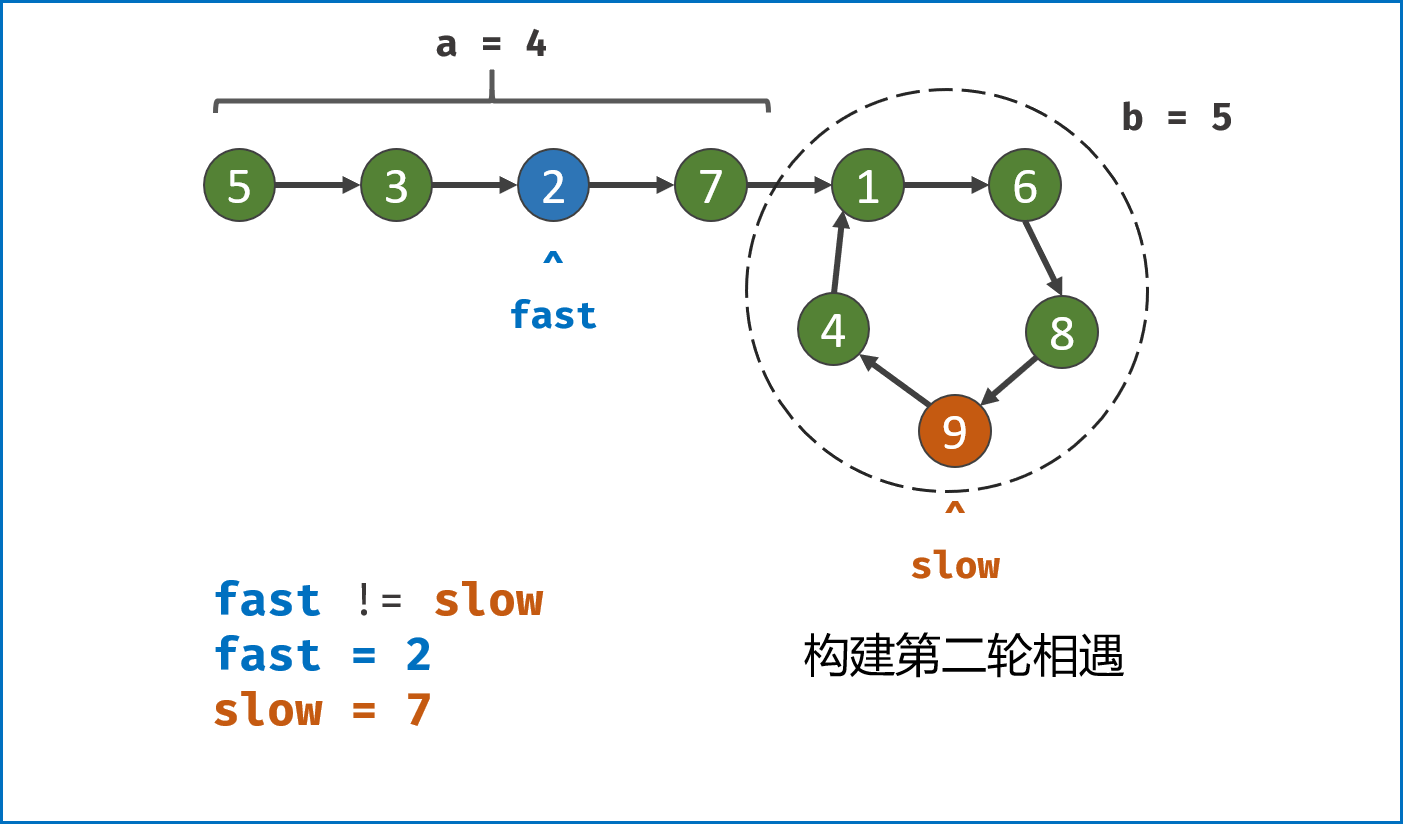
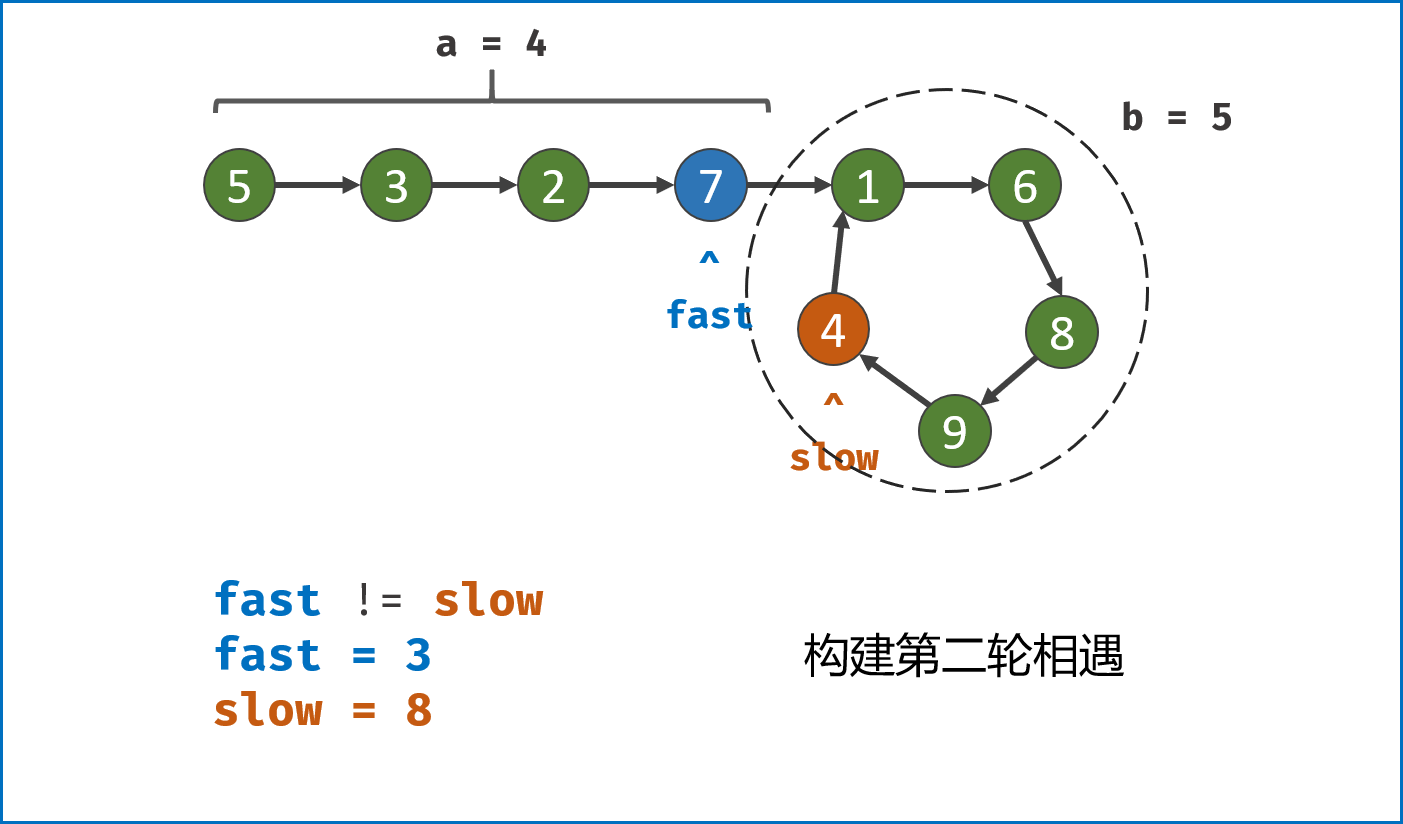
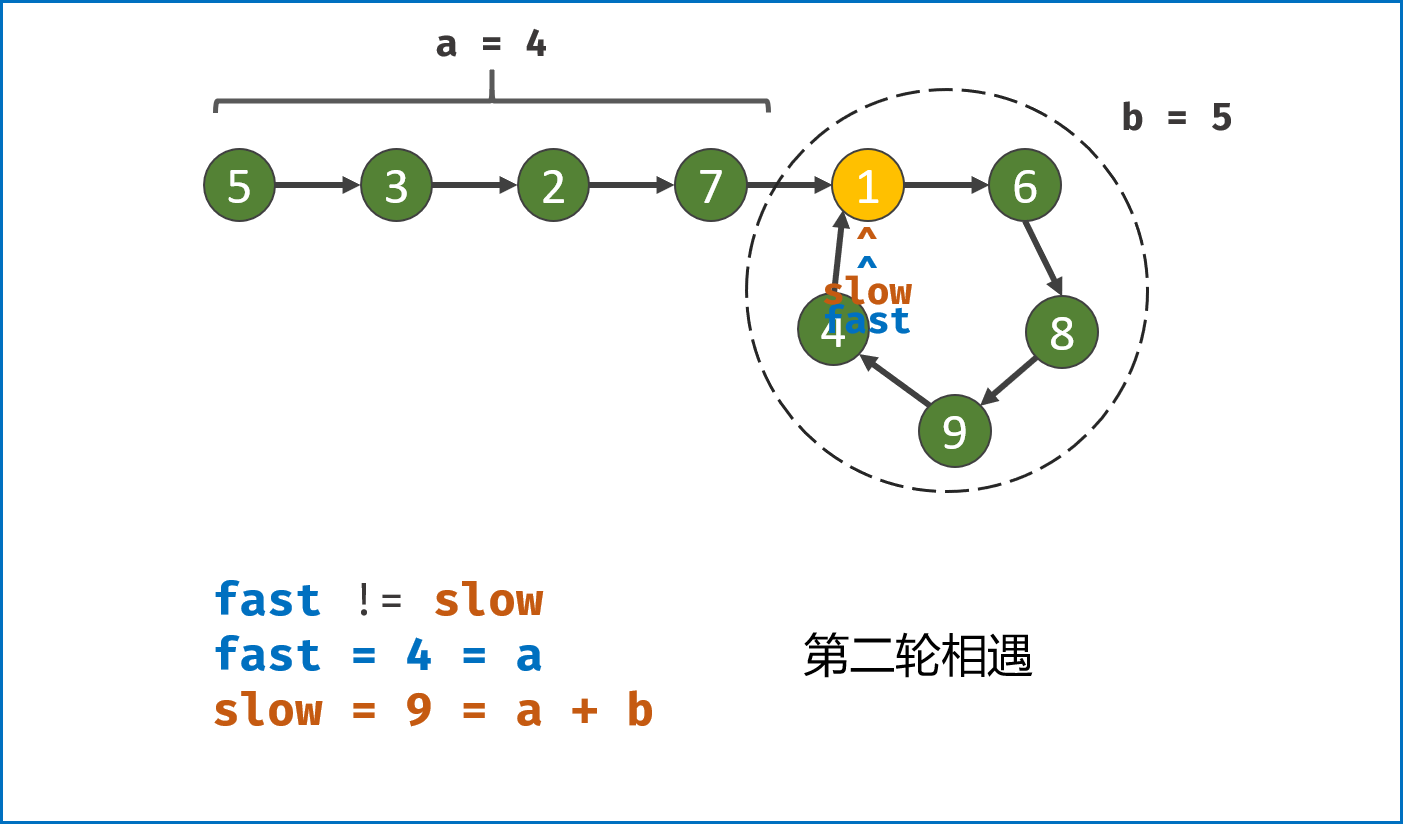
双指针第二次相遇：

  1. 令 fast 重新指向链表头部节点。此时 $f = 0$，$s = nb$ 。
  2. slow 和 fast 同时每轮向前走 $1$ 步。
  3. 当 fast 指针走到 $f = a$ 步时，slow 指针走到 $s = a+nb$ 步。此时两指针重合，并同时指向链表环入口，返回 slow 指向的节点即可。

<Picture1.png,Picture2.png,Picture3.png,Picture4.png,Picture5.png,Picture6.png,Picture7.png,Picture8.png,Picture9.png,Picture10.png,Picture11.png>

代码：

[]
1
2
3
4
5
6
7
8
9
10
11
class Solution(object):
    def detectCycle(self, head):
        fast, slow = head, head
        while True:
            if not (fast and fast.next): return
            fast, slow = fast.next.next, slow.next
            if fast == slow: break
        fast = head
        while fast != slow:
            fast, slow = fast.next, slow.next
        return fast
[]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode fast = head, slow = head;
        while (true) {
            if (fast == null || fast.next == null) return null;
            fast = fast.next.next;
            slow = slow.next;
            if (fast == slow) break;
        }
        fast = head;
        while (slow != fast) {
            slow = slow.next;
            fast = fast.next;
        }
        return fast;
    }
}
[]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* fast = head;
        ListNode* slow = head;
        while (true) {
            if (fast == nullptr || fast->next == nullptr) return nullptr;
            fast = fast->next->next;
            slow = slow->next;
            if (fast == slow) break;
        }
        fast = head;
        while (slow != fast) {
            slow = slow->next;
            fast = fast->next;
        }
        return fast;
    }
};

复杂度分析：

  • 时间复杂度 $O(N)$ ：第二次相遇中，慢指针须走步数 $a < a + b$；第一次相遇中，慢指针须走步数 $a + b - x < a + b$，其中 $x$ 为双指针重合点与环入口距离；因此总体为线性复杂度；
  • 空间复杂度 $O(1)$ ：双指针使用常数大小的额外空间。

link

本学习计划配有代码仓，内含测试样例与数据结构封装，便于本地调试。可前往我的个人主页 获取。

 Comments
On this page
0142-环形链表 II
  1. 解题思路：
  2. 代码：
    1. 复杂度分析：