给你一棵二叉树的根节点 root ,返回其节点值的 后序遍历 。
示例 1:

**输入:** root = [1,null,2,3]
**输出:** [3,2,1]
示例 2:
**输入:** root = []
**输出:** []
示例 3:
**输入:** root = [1]
**输出:** [1]
提示:
- 树中节点的数目在范围
[0, 100] 内
-100 <= Node.val <= 100
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
方法一:递归
思路与算法
首先我们需要了解什么是二叉树的后序遍历:按照访问左子树——右子树——根节点的方式遍历这棵树,而在访问左子树或者右子树的时候,我们按照同样的方式遍历,直到遍历完整棵树。因此整个遍历过程天然具有递归的性质,我们可以直接用递归函数来模拟这一过程。
定义 postorder(root) 表示当前遍历到 root 节点的答案。按照定义,我们只要递归调用 postorder(root->left) 来遍历 root 节点的左子树,然后递归调用 postorder(root->right) 来遍历 root 节点的右子树,最后将 root 节点的值加入答案即可,递归终止的条件为碰到空节点。
代码
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
public:
void postorder(TreeNode *root, vector<int> &res) {
if (root == nullptr) {
return;
}
postorder(root->left, res);
postorder(root->right, res);
res.push_back(root->val);
}
vector<int> postorderTraversal(TreeNode *root) {
vector<int> res;
postorder(root, res);
return res;
}
};
|
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
postorder(root, res);
return res;
}
public void postorder(TreeNode root, List<Integer> res) {
if (root == null) {
return;
}
postorder(root.left, res);
postorder(root.right, res);
res.add(root.val);
}
}
|
[sol1-Python3]1
2
3
4
5
6
7
8
9
10
11
12
| class Solution:
def postorderTraversal(self, root: TreeNode) -> List[int]:
def postorder(root: TreeNode):
if not root:
return
postorder(root.left)
postorder(root.right)
res.append(root.val)
res = list()
postorder(root)
return res
|
[sol1-Golang]1
2
3
4
5
6
7
8
9
10
11
12
13
| func postorderTraversal(root *TreeNode) (res []int) {
var postorder func(*TreeNode)
postorder = func(node *TreeNode) {
if node == nil {
return
}
postorder(node.Left)
postorder(node.Right)
res = append(res, node.Val)
}
postorder(root)
return
}
|
[sol1-C]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| void postorder(struct TreeNode *root, int *res, int *resSize) {
if (root == NULL) {
return;
}
postorder(root->left, res, resSize);
postorder(root->right, res, resSize);
res[(*resSize)++] = root->val;
}
int *postorderTraversal(struct TreeNode *root, int *returnSize) {
int *res = malloc(sizeof(int) * 2001);
*returnSize = 0;
postorder(root, res, returnSize);
return res;
}
|
复杂度分析
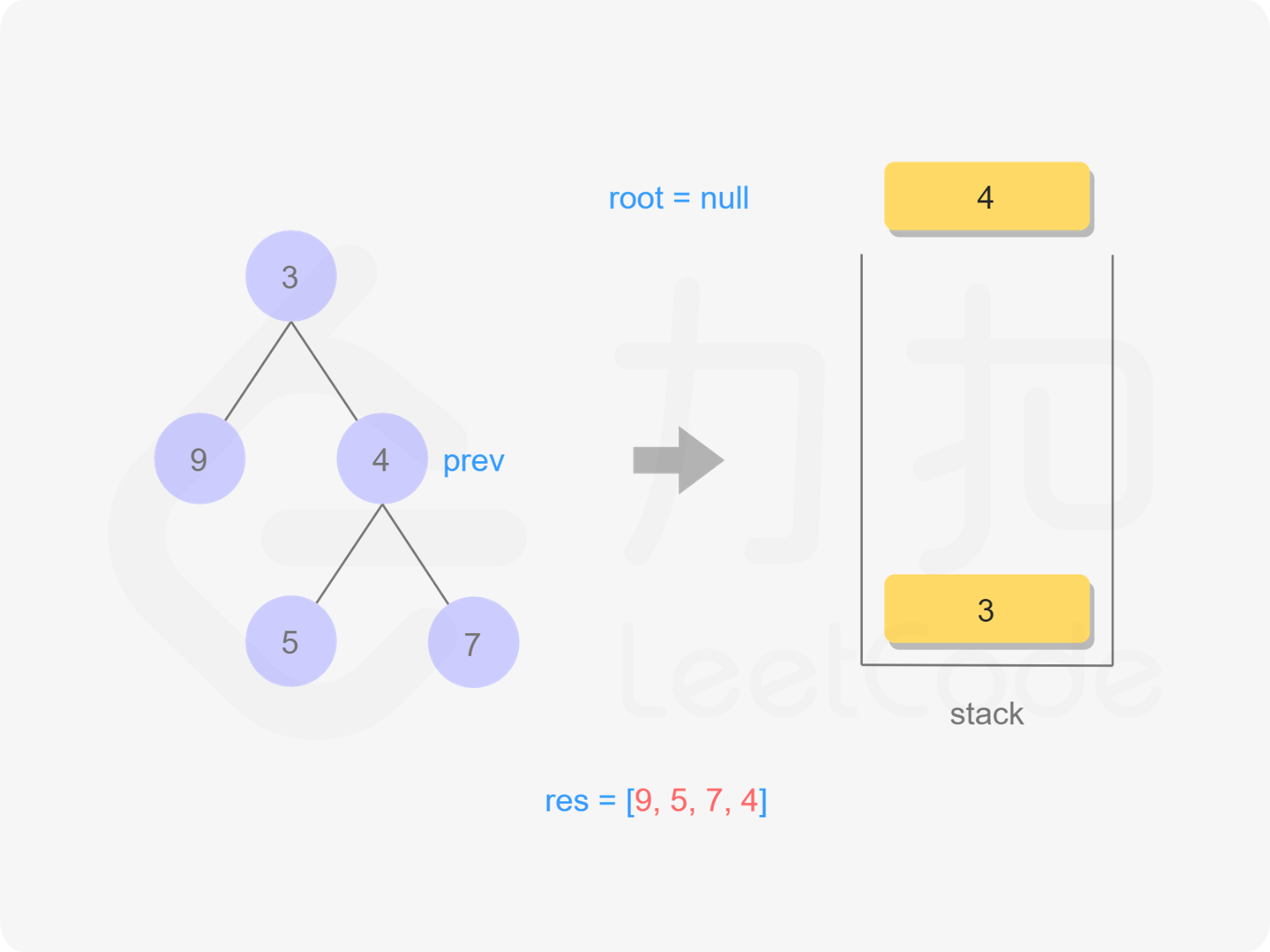
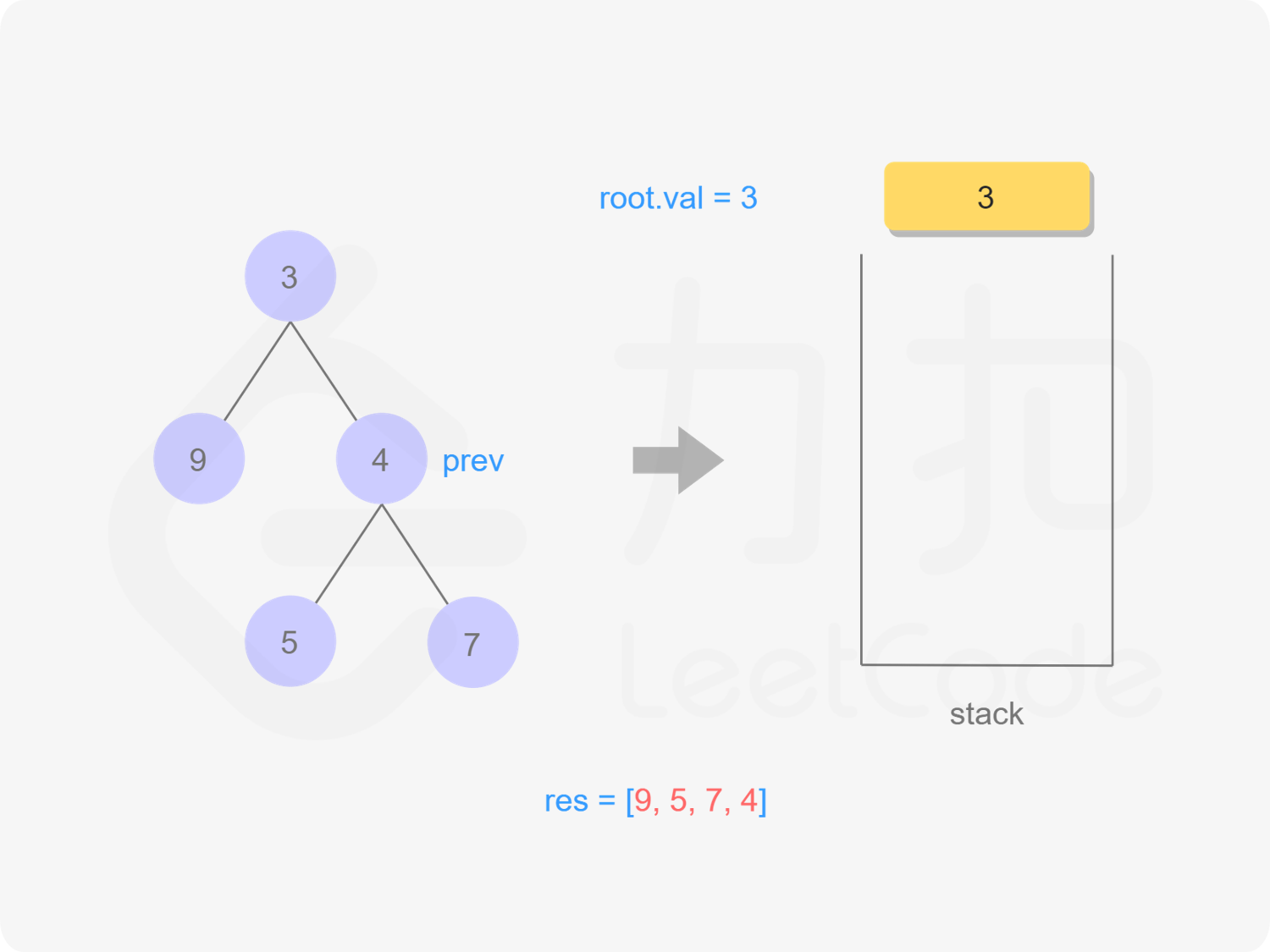
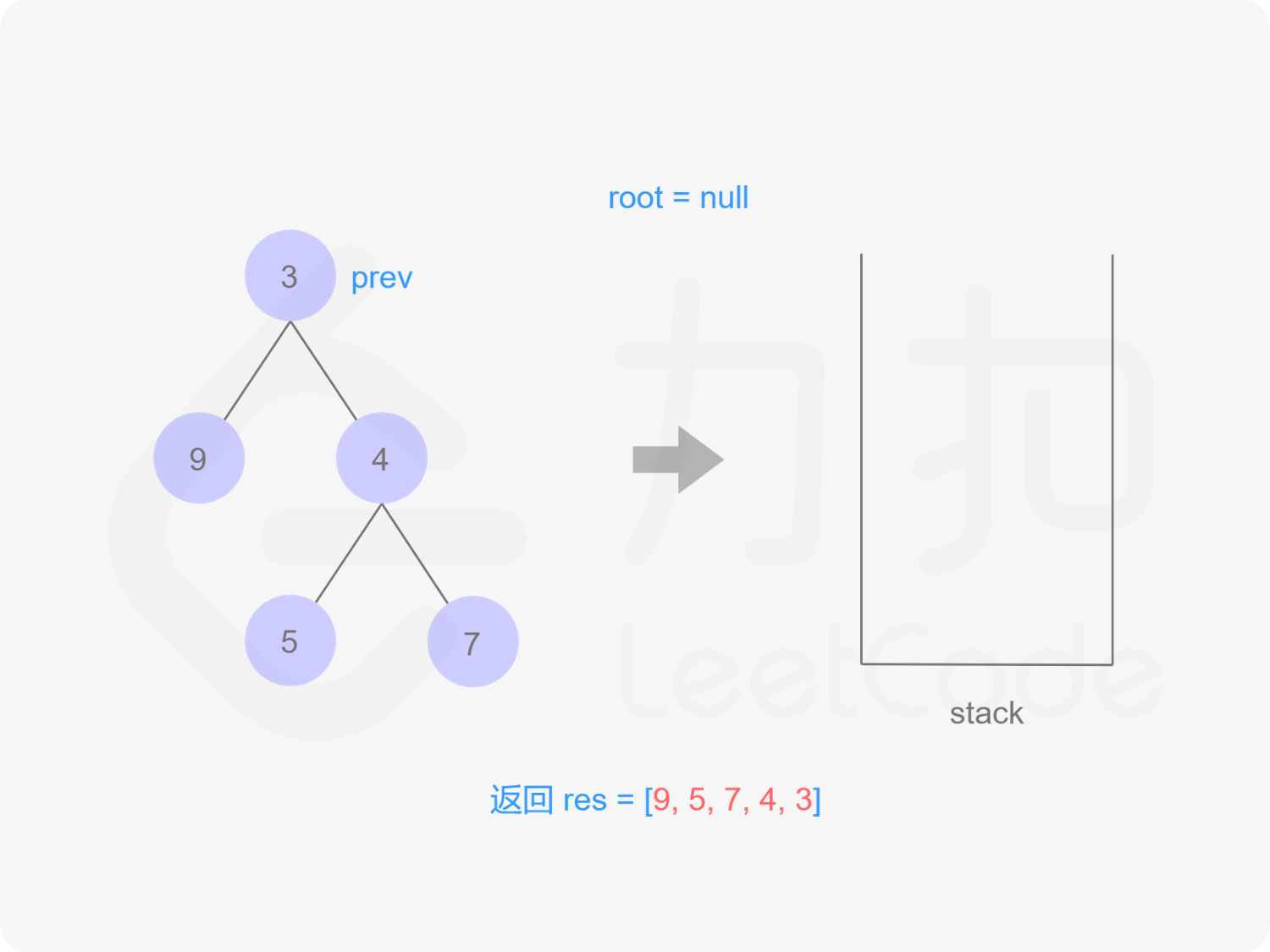
方法二:迭代
思路与算法
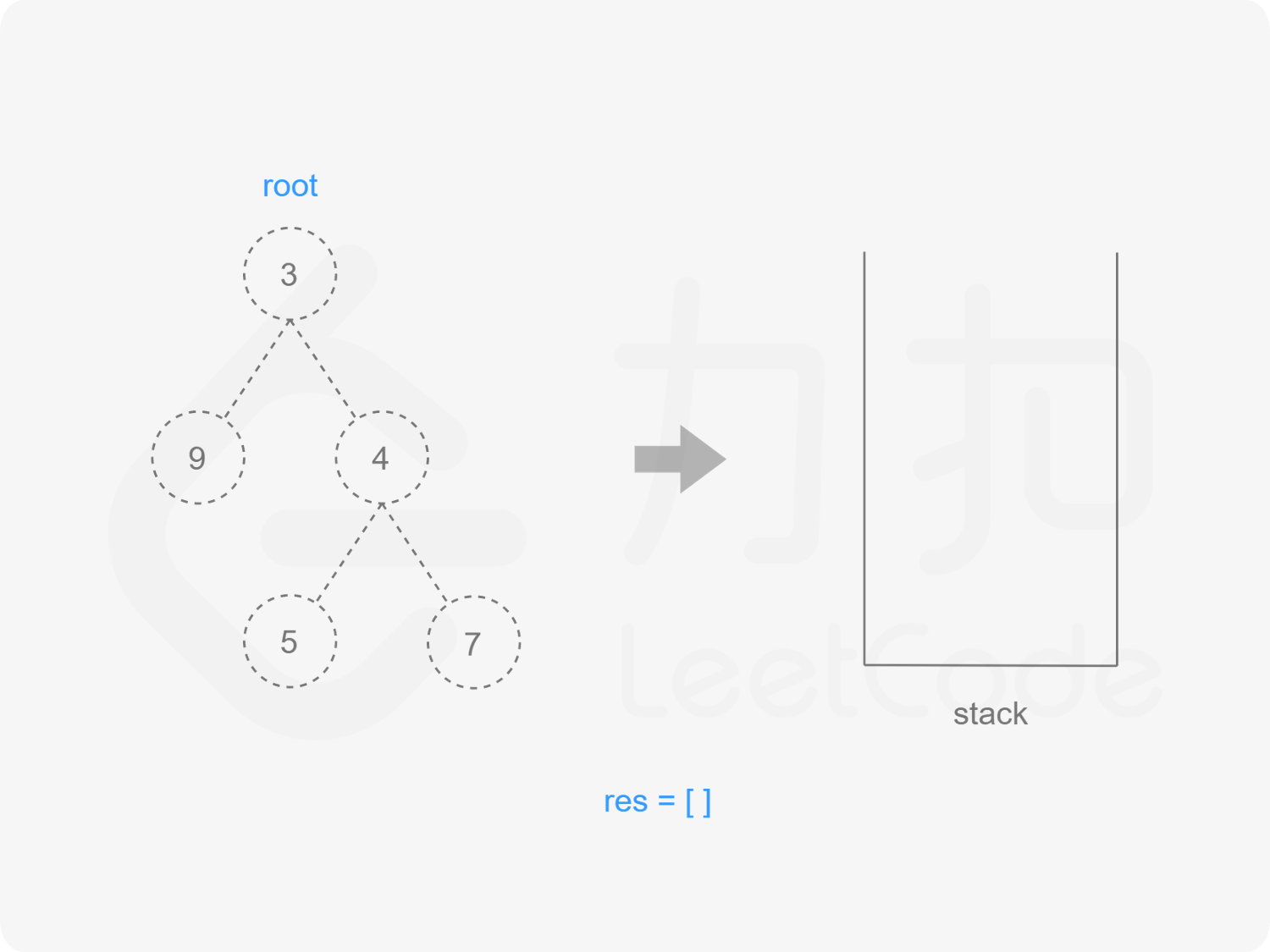
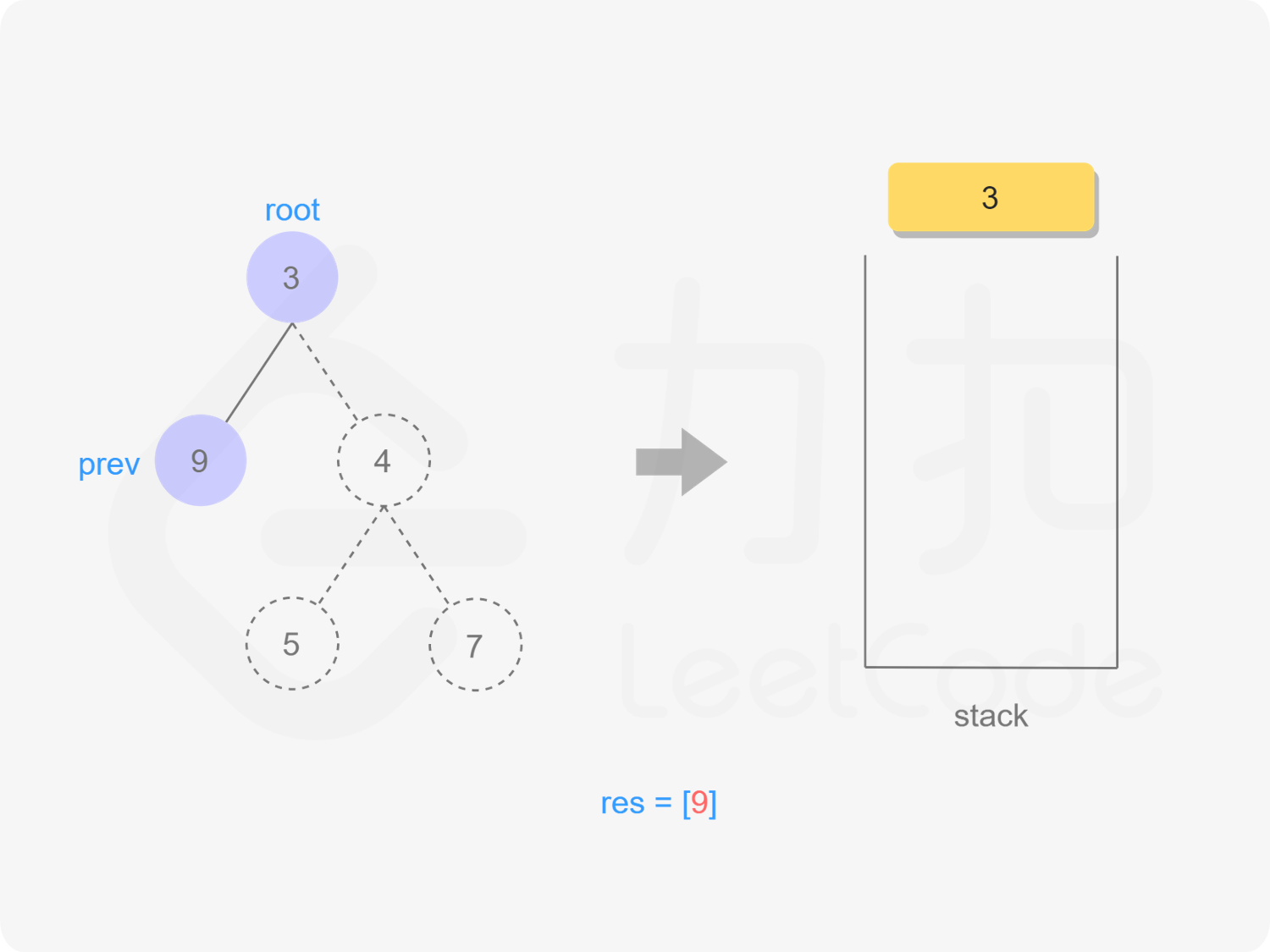
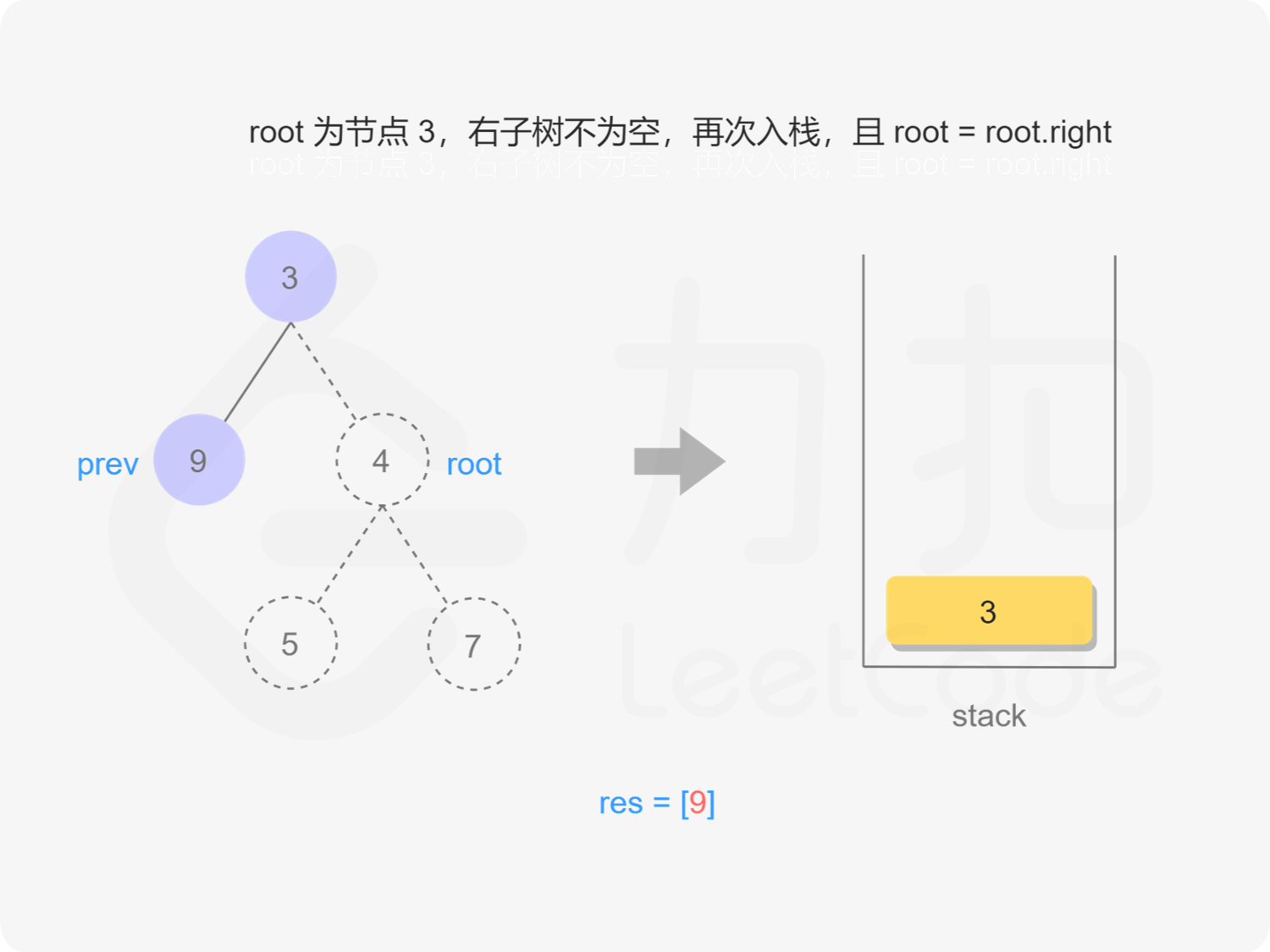
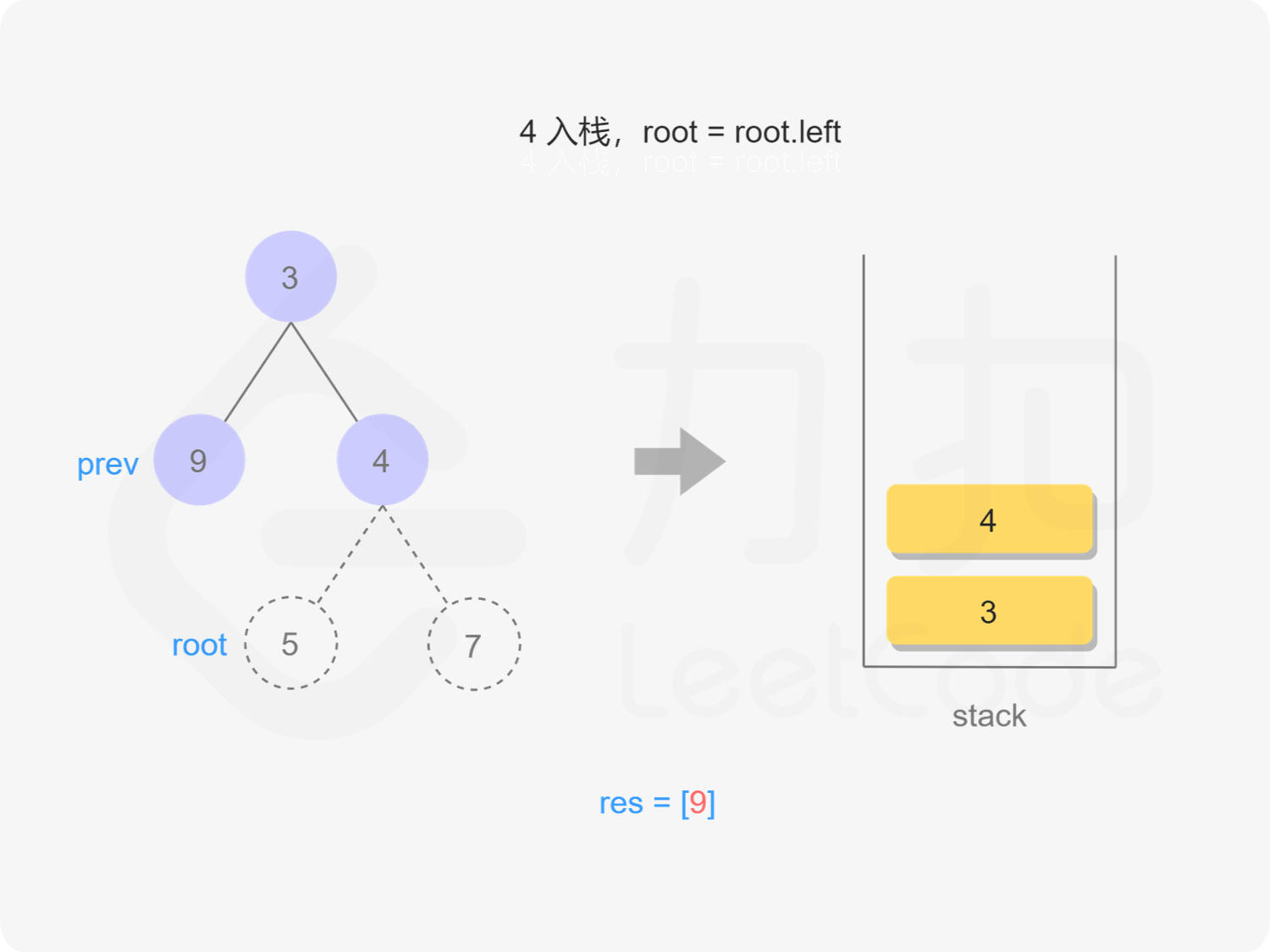
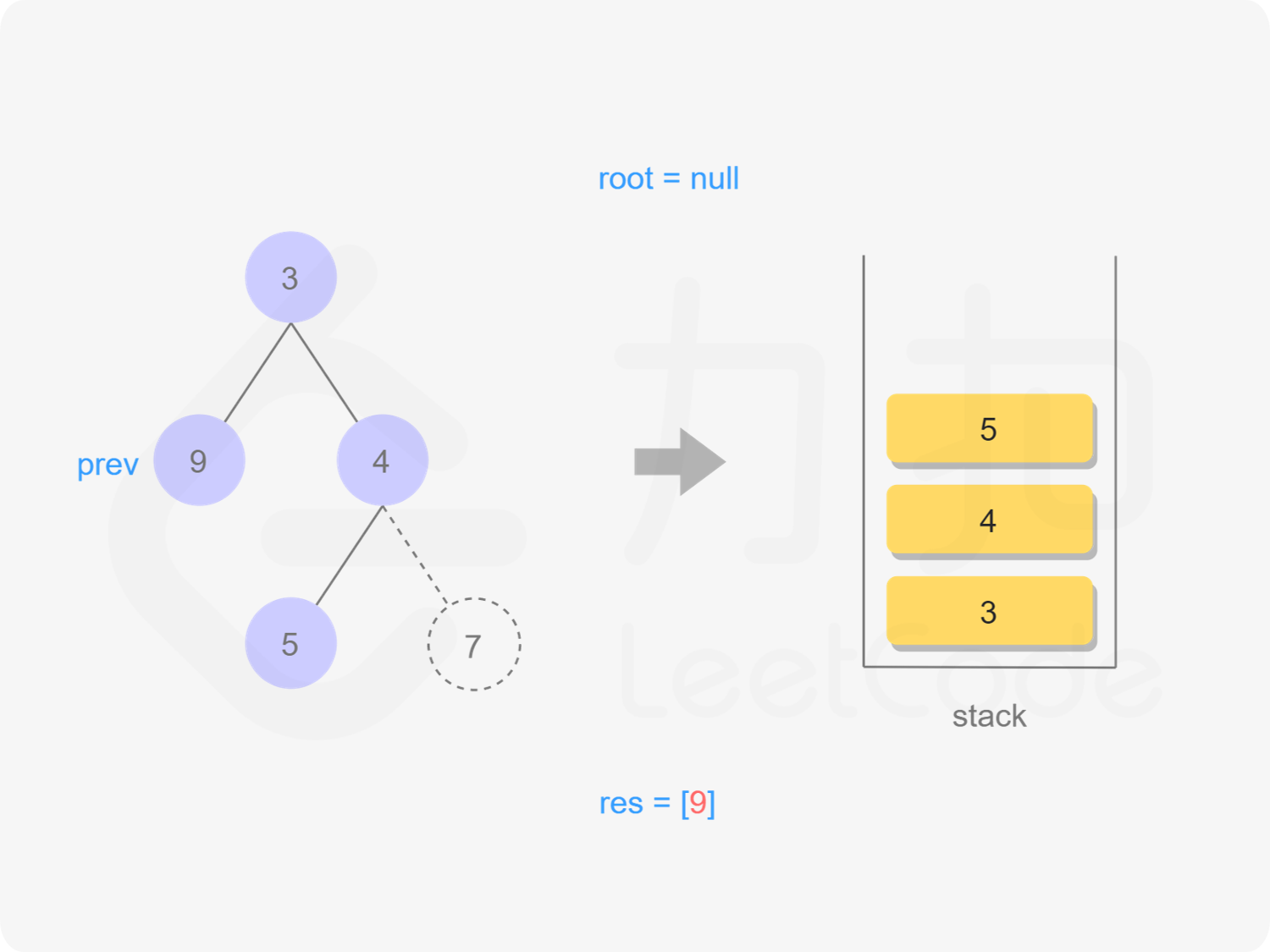
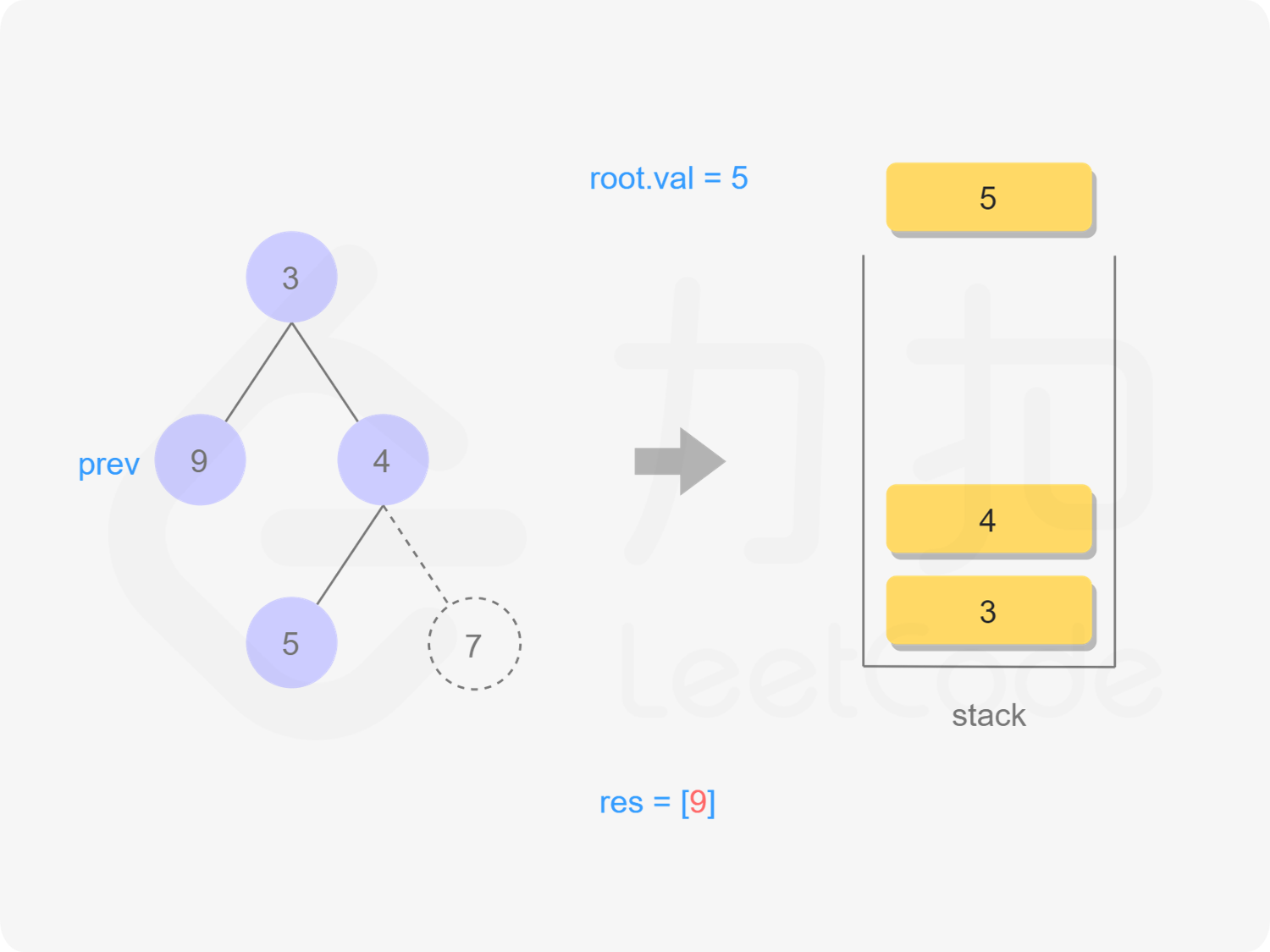
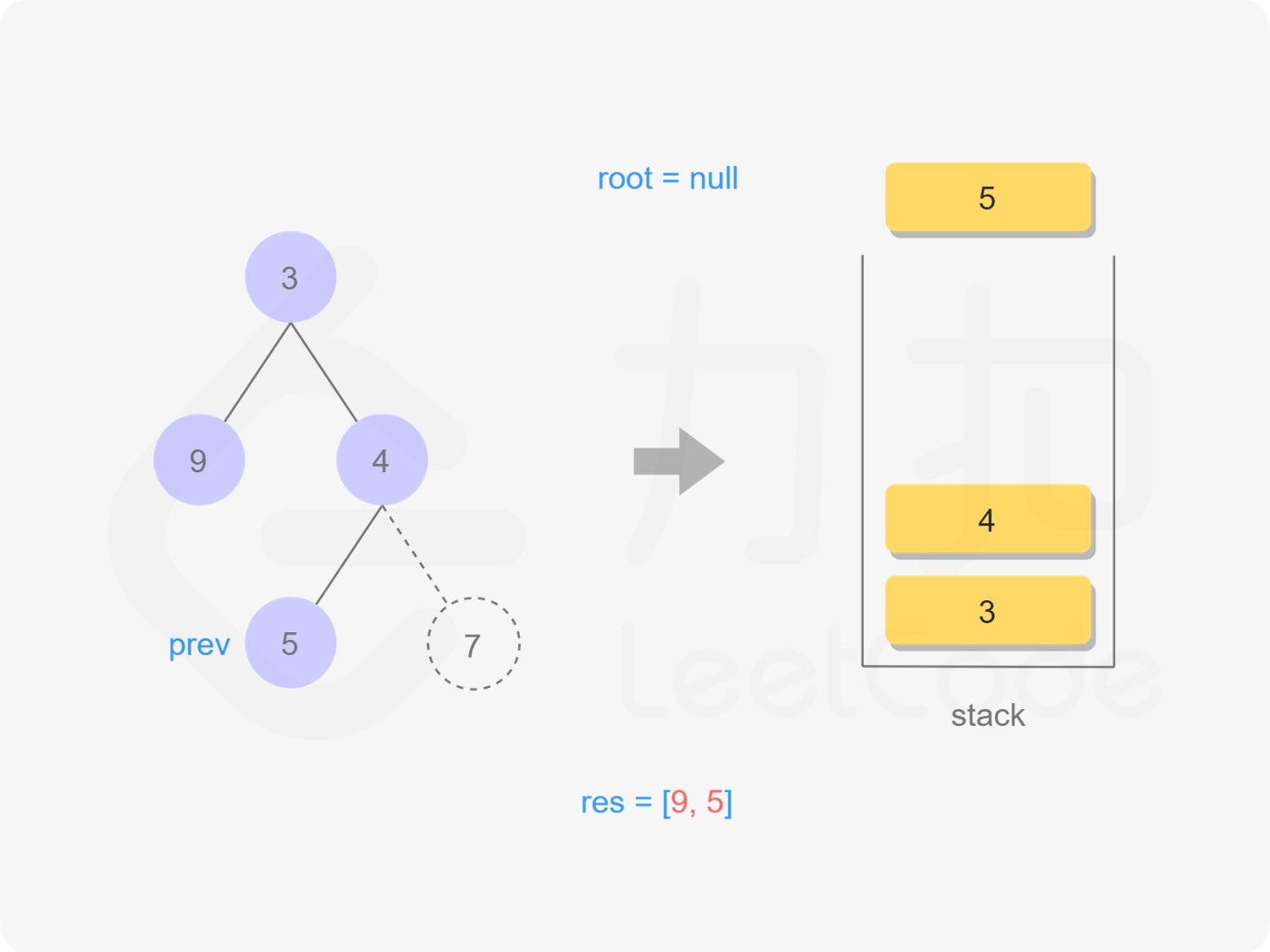
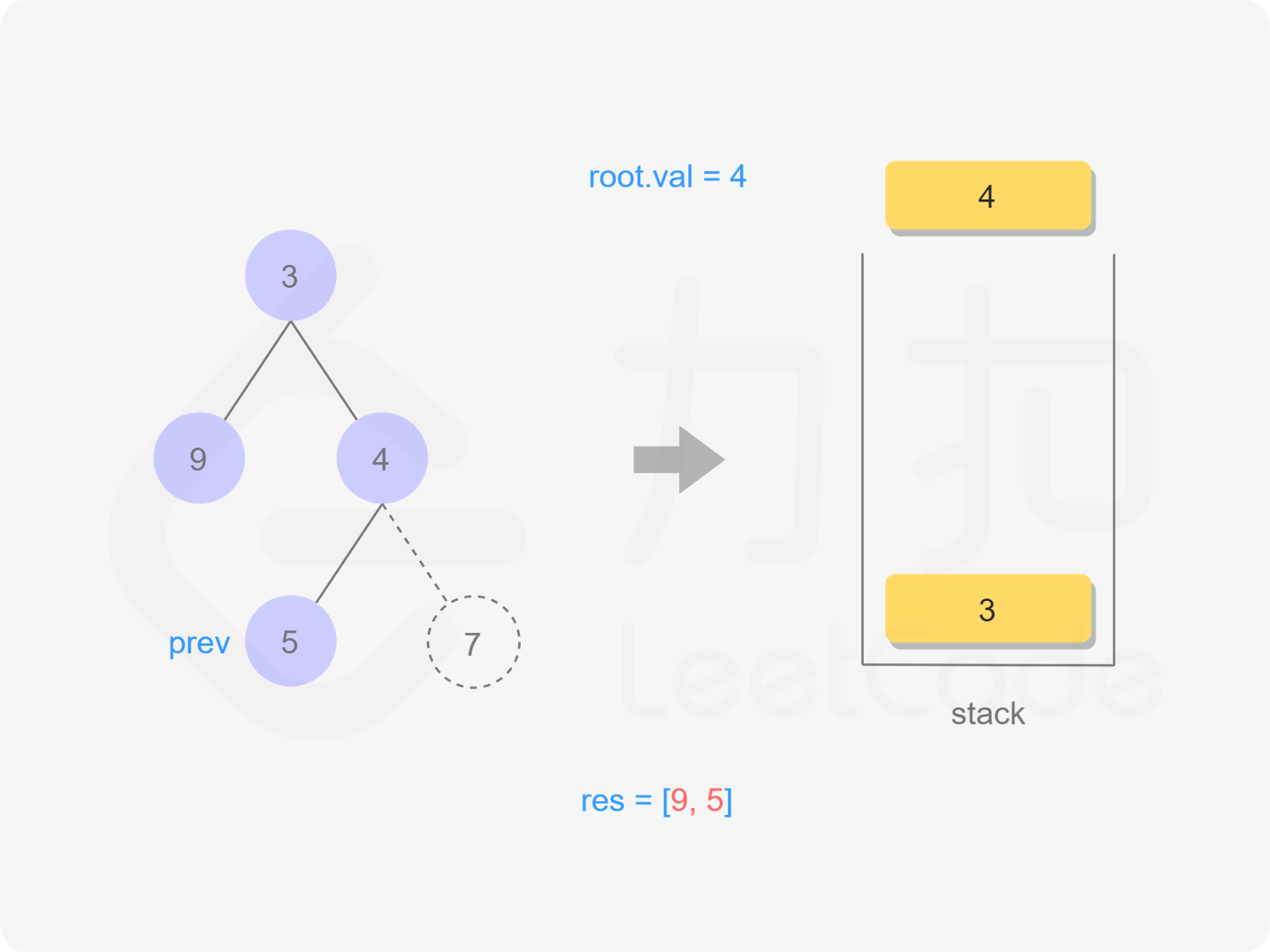
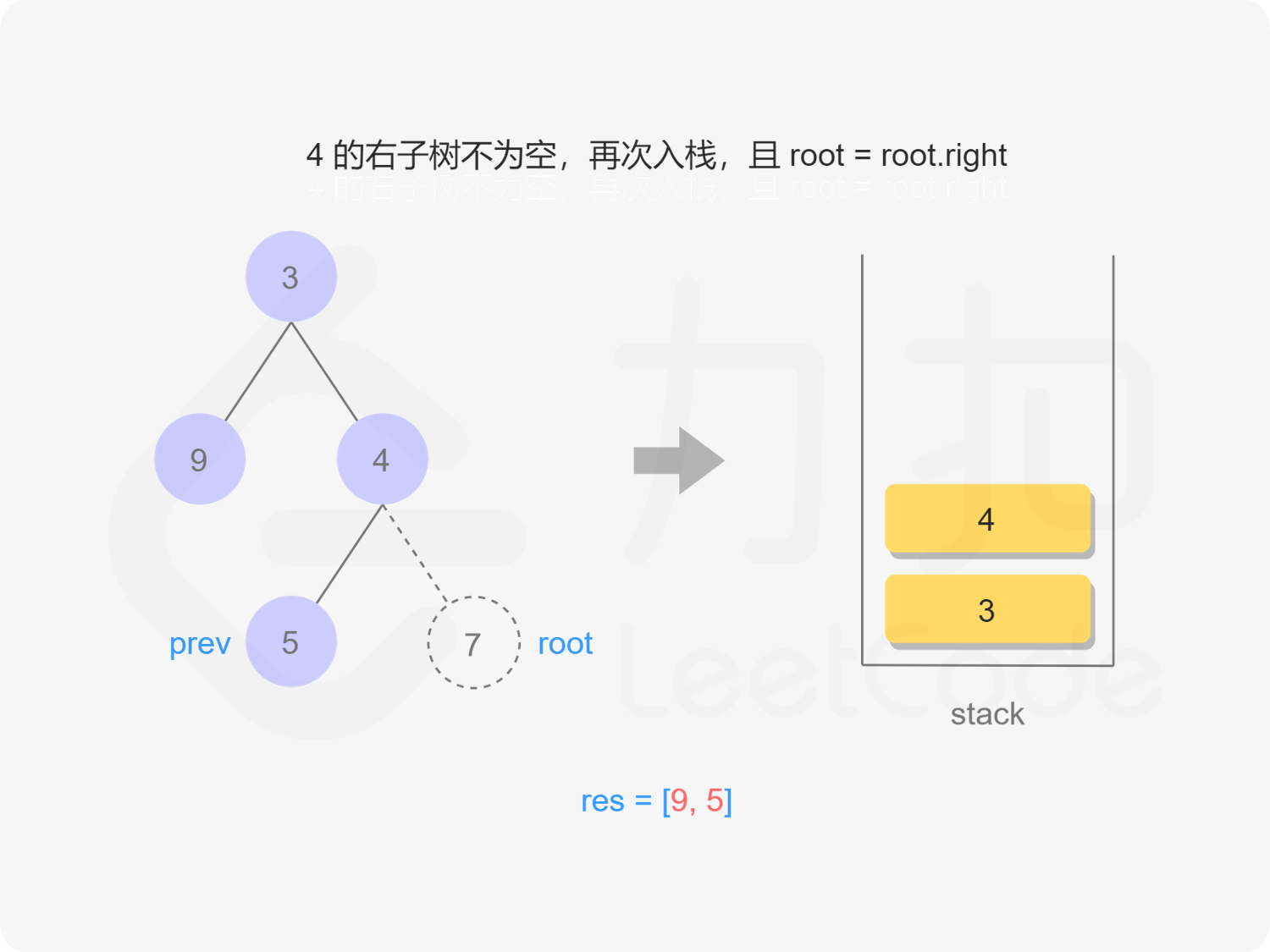
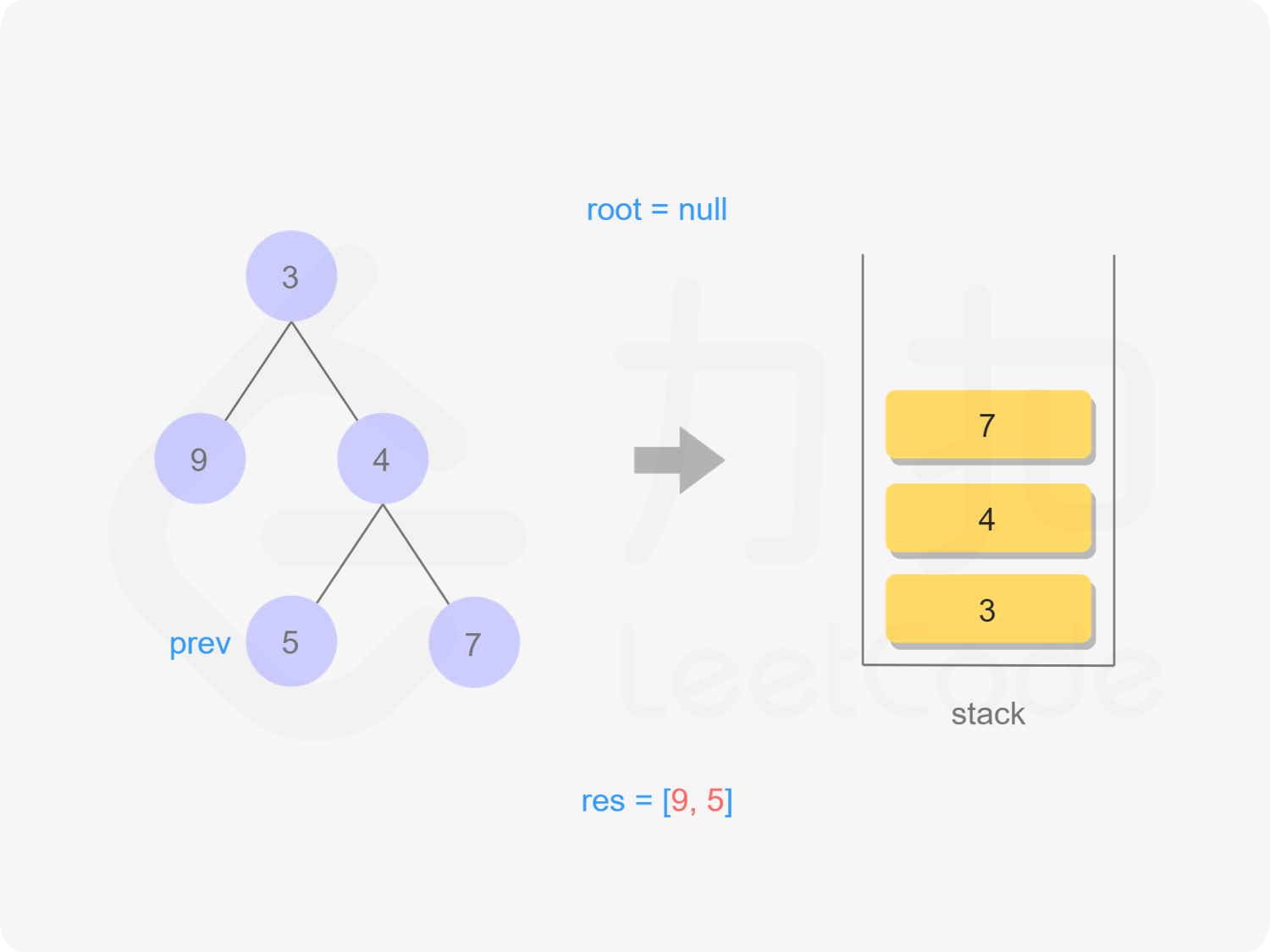
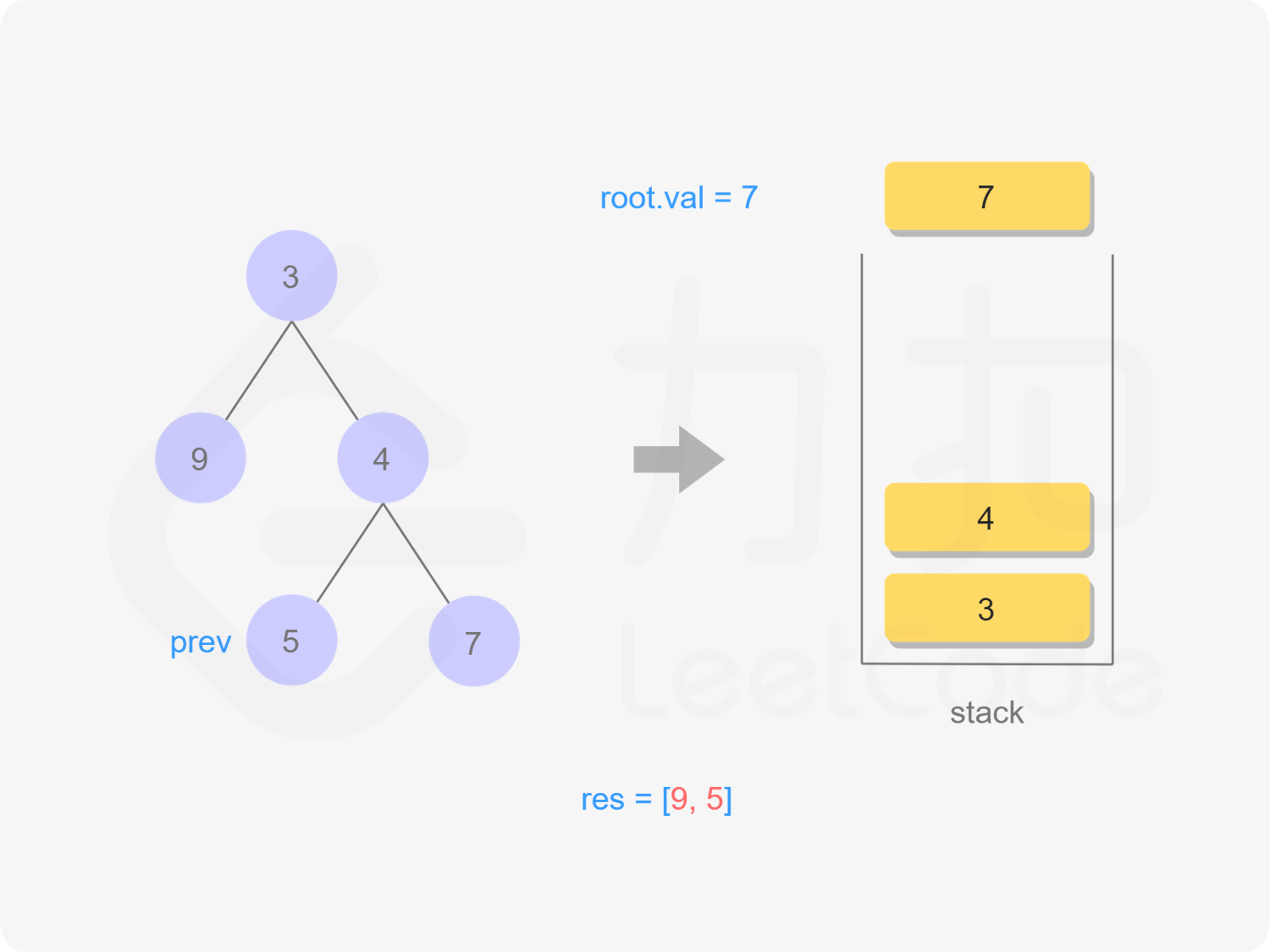
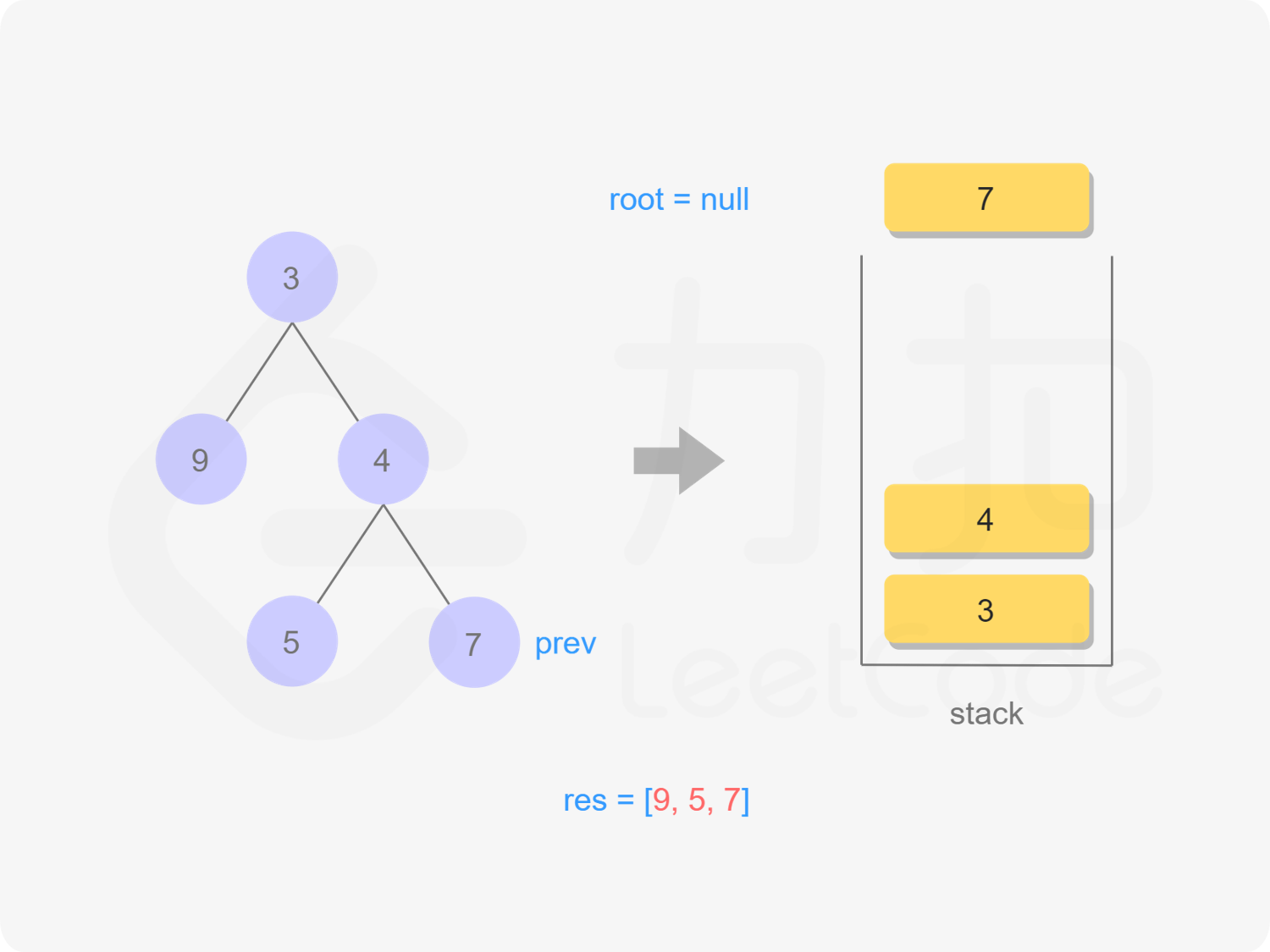
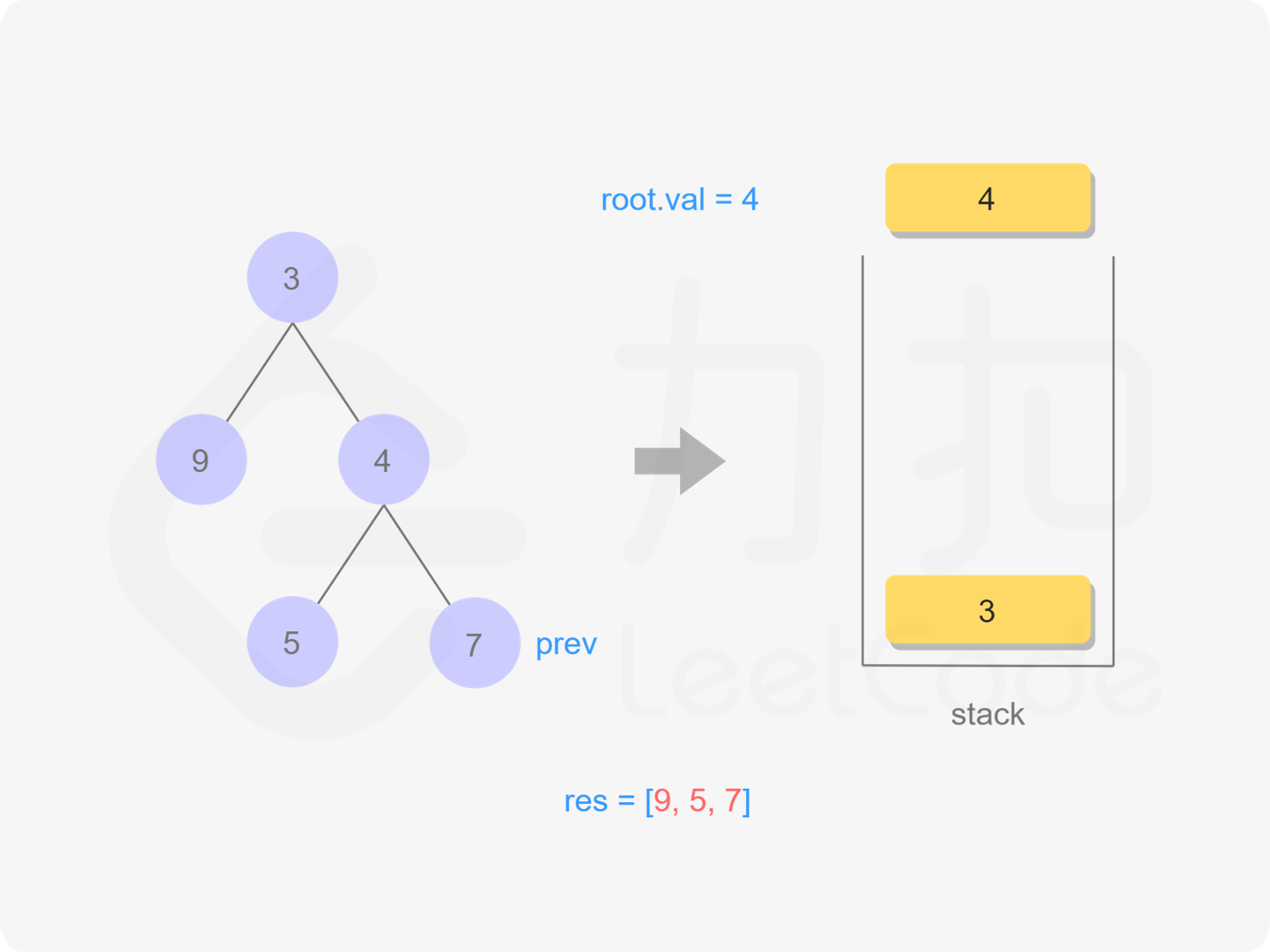
我们也可以用迭代的方式实现方法一的递归函数,两种方式是等价的,区别在于递归的时候隐式地维护了一个栈,而我们在迭代的时候需要显式地将这个栈模拟出来,其余的实现与细节都相同,具体可以参考下面的代码。
< ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>
代码
[sol2-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| class Solution {
public:
vector<int> postorderTraversal(TreeNode *root) {
vector<int> res;
if (root == nullptr) {
return res;
}
stack<TreeNode *> stk;
TreeNode *prev = nullptr;
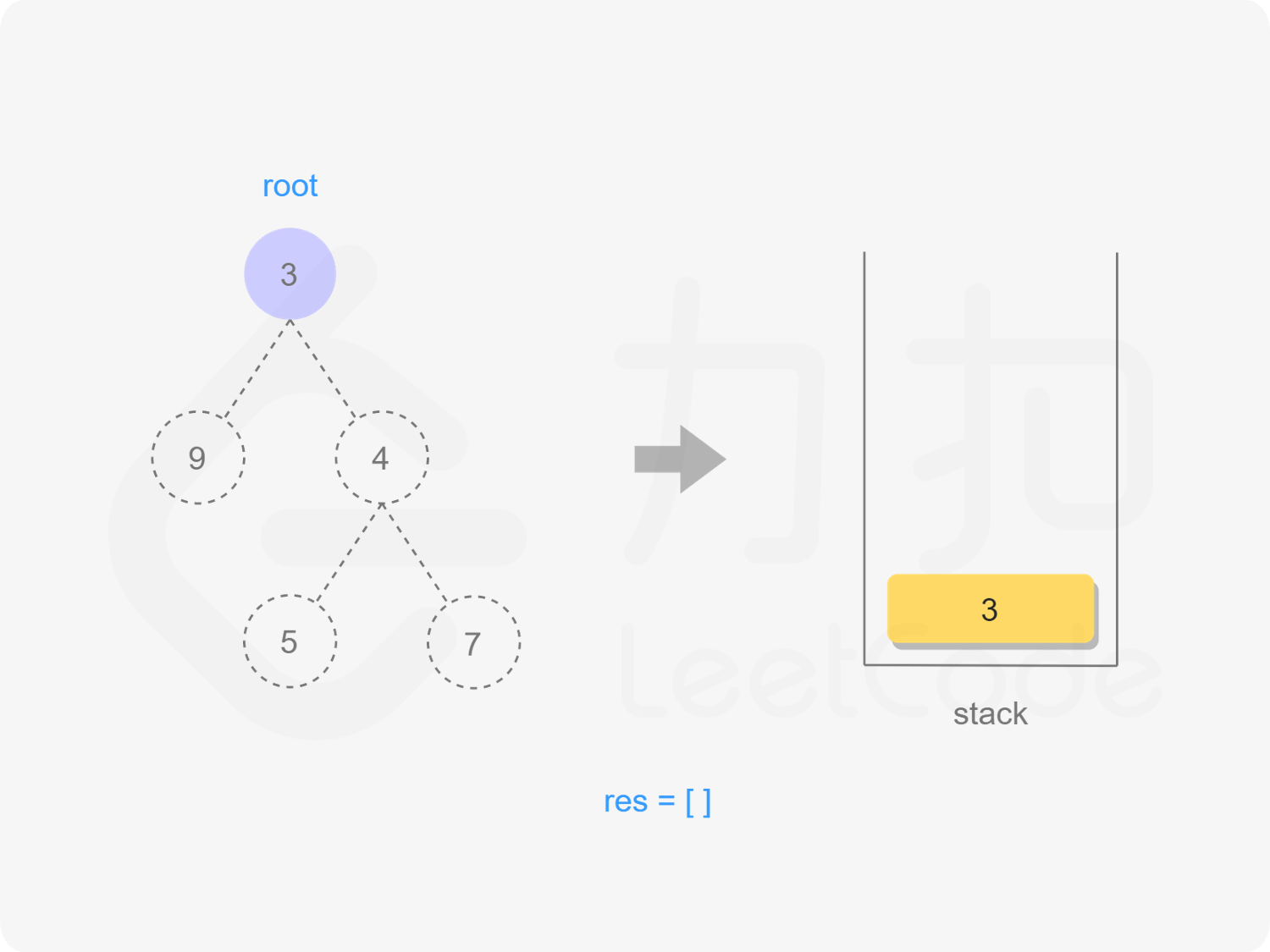
while (root != nullptr || !stk.empty()) {
while (root != nullptr) {
stk.emplace(root);
root = root->left;
}
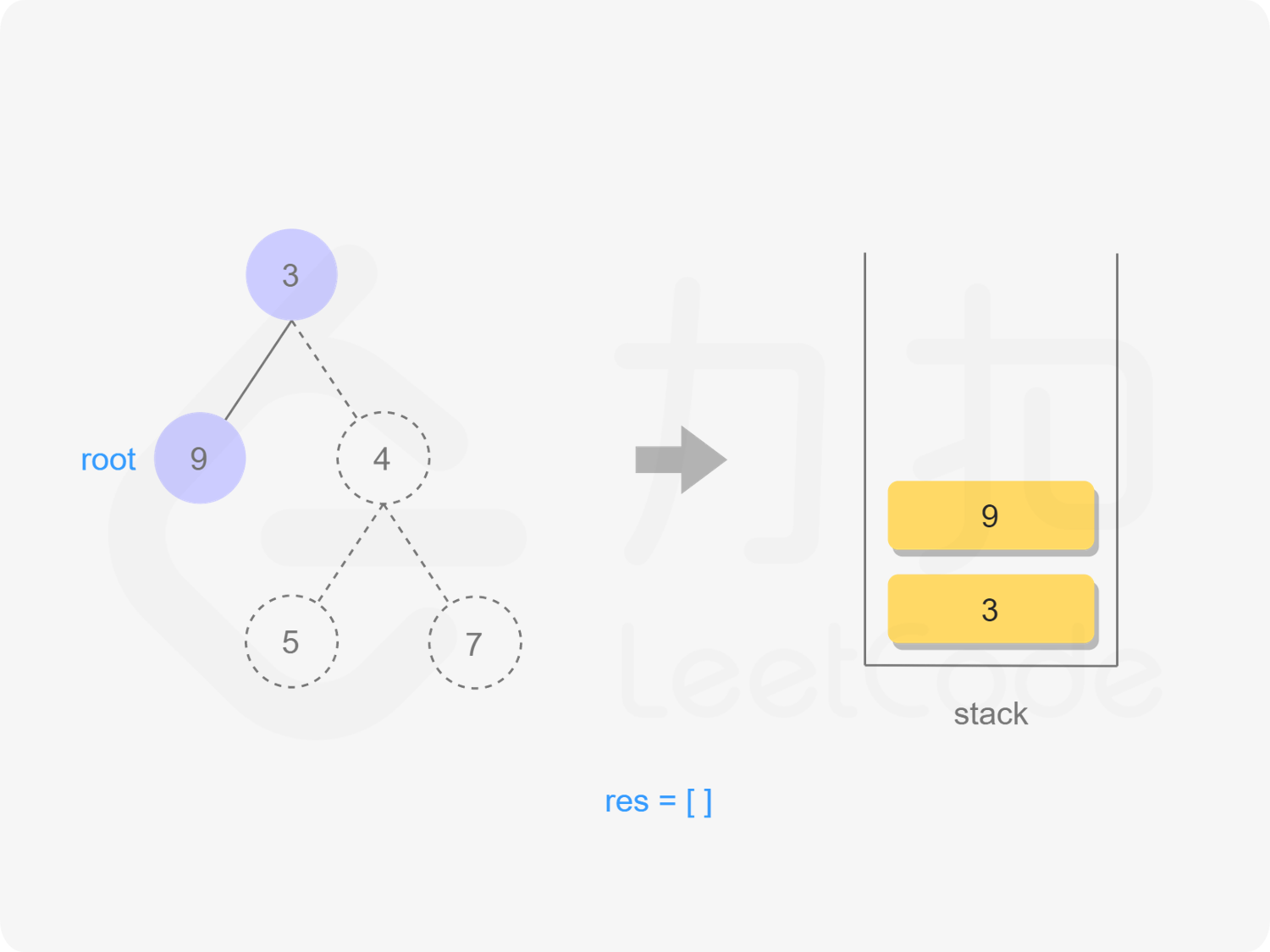
root = stk.top();
stk.pop();
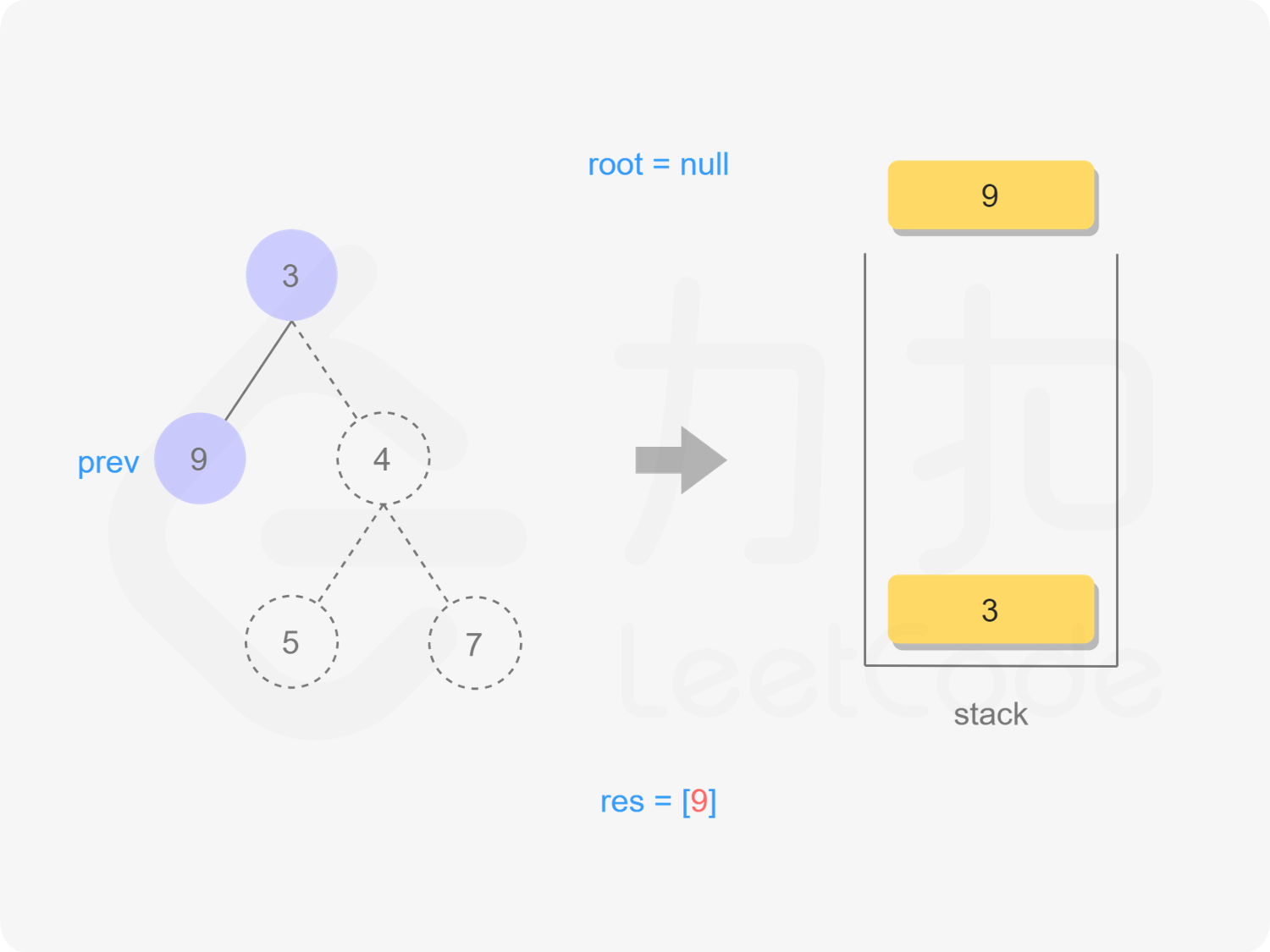
if (root->right == nullptr || root->right == prev) {
res.emplace_back(root->val);
prev = root;
root = nullptr;
} else {
stk.emplace(root);
root = root->right;
}
}
return res;
}
};
|
[sol2-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
if (root == null) {
return res;
}
Deque<TreeNode> stack = new LinkedList<TreeNode>();
TreeNode prev = null;
while (root != null || !stack.isEmpty()) {
while (root != null) {
stack.push(root);
root = root.left;
}
root = stack.pop();
if (root.right == null || root.right == prev) {
res.add(root.val);
prev = root;
root = null;
} else {
stack.push(root);
root = root.right;
}
}
return res;
}
}
|
[sol2-Python3]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class Solution:
def postorderTraversal(self, root: TreeNode) -> List[int]:
if not root:
return list()
res = list()
stack = list()
prev = None
while root or stack:
while root:
stack.append(root)
root = root.left
root = stack.pop()
if not root.right or root.right == prev:
res.append(root.val)
prev = root
root = None
else:
stack.append(root)
root = root.right
return res
|
[sol2-Golang]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| func postorderTraversal(root *TreeNode) (res []int) {
stk := []*TreeNode{}
var prev *TreeNode
for root != nil || len(stk) > 0 {
for root != nil {
stk = append(stk, root)
root = root.Left
}
root = stk[len(stk)-1]
stk = stk[:len(stk)-1]
if root.Right == nil || root.Right == prev {
res = append(res, root.Val)
prev = root
root = nil
} else {
stk = append(stk, root)
root = root.Right
}
}
return
}
|
[sol2-C]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| int *postorderTraversal(struct TreeNode *root, int *returnSize) {
int *res = malloc(sizeof(int) * 2001);
*returnSize = 0;
if (root == NULL) {
return res;
}
struct TreeNode **stk = malloc(sizeof(struct TreeNode *) * 2001);
int top = 0;
struct TreeNode *prev = NULL;
while (root != NULL || top > 0) {
while (root != NULL) {
stk[top++] = root;
root = root->left;
}
root = stk[--top];
if (root->right == NULL || root->right == prev) {
res[(*returnSize)++] = root->val;
prev = root;
root = NULL;
} else {
stk[top++] = root;
root = root->right;
}
}
return res;
}
|
复杂度分析
方法三:Morris 遍历
思路与算法
有一种巧妙的方法可以在线性时间内,只占用常数空间来实现后序遍历。这种方法由 J. H. Morris 在 1979 年的论文「Traversing Binary Trees Simply and Cheaply」中首次提出,因此被称为 Morris 遍历。
Morris 遍历的核心思想是利用树的大量空闲指针,实现空间开销的极限缩减。其后序遍历规则总结如下:
新建临时节点,令该节点为 root;
如果当前节点的左子节点为空,则遍历当前节点的右子节点;
如果当前节点的左子节点不为空,在当前节点的左子树中找到当前节点在中序遍历下的前驱节点;
重复步骤 2 和步骤 3,直到遍历结束。
这样我们利用 Morris 遍历的方法,后序遍历该二叉搜索树,即可实现线性时间与常数空间的遍历。
代码
[sol3-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| class Solution {
public:
void addPath(vector<int> &vec, TreeNode *node) {
int count = 0;
while (node != nullptr) {
++count;
vec.emplace_back(node->val);
node = node->right;
}
reverse(vec.end() - count, vec.end());
}
vector<int> postorderTraversal(TreeNode *root) {
vector<int> res;
if (root == nullptr) {
return res;
}
TreeNode *p1 = root, *p2 = nullptr;
while (p1 != nullptr) {
p2 = p1->left;
if (p2 != nullptr) {
while (p2->right != nullptr && p2->right != p1) {
p2 = p2->right;
}
if (p2->right == nullptr) {
p2->right = p1;
p1 = p1->left;
continue;
} else {
p2->right = nullptr;
addPath(res, p1->left);
}
}
p1 = p1->right;
}
addPath(res, root);
return res;
}
};
|
[sol3-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
if (root == null) {
return res;
}
TreeNode p1 = root, p2 = null;
while (p1 != null) {
p2 = p1.left;
if (p2 != null) {
while (p2.right != null && p2.right != p1) {
p2 = p2.right;
}
if (p2.right == null) {
p2.right = p1;
p1 = p1.left;
continue;
} else {
p2.right = null;
addPath(res, p1.left);
}
}
p1 = p1.right;
}
addPath(res, root);
return res;
}
public void addPath(List<Integer> res, TreeNode node) {
int count = 0;
while (node != null) {
++count;
res.add(node.val);
node = node.right;
}
int left = res.size() - count, right = res.size() - 1;
while (left < right) {
int temp = res.get(left);
res.set(left, res.get(right));
res.set(right, temp);
left++;
right--;
}
}
}
|
[sol3-Python3]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| class Solution:
def postorderTraversal(self, root: TreeNode) -> List[int]:
def addPath(node: TreeNode):
count = 0
while node:
count += 1
res.append(node.val)
node = node.right
i, j = len(res) - count, len(res) - 1
while i < j:
res[i], res[j] = res[j], res[i]
i += 1
j -= 1
if not root:
return list()
res = list()
p1 = root
while p1:
p2 = p1.left
if p2:
while p2.right and p2.right != p1:
p2 = p2.right
if not p2.right:
p2.right = p1
p1 = p1.left
continue
else:
p2.right = None
addPath(p1.left)
p1 = p1.right
addPath(root)
return res
|
[sol3-Golang]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| func reverse(a []int) {
for i, n := 0, len(a); i < n/2; i++ {
a[i], a[n-1-i] = a[n-1-i], a[i]
}
}
func postorderTraversal(root *TreeNode) (res []int) {
addPath := func(node *TreeNode) {
resSize := len(res)
for ; node != nil; node = node.Right {
res = append(res, node.Val)
}
reverse(res[resSize:])
}
p1 := root
for p1 != nil {
if p2 := p1.Left; p2 != nil {
for p2.Right != nil && p2.Right != p1 {
p2 = p2.Right
}
if p2.Right == nil {
p2.Right = p1
p1 = p1.Left
continue
}
p2.Right = nil
addPath(p1.Left)
}
p1 = p1.Right
}
addPath(root)
return
}
|
[sol3-C]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| void addPath(int *vec, int *vecSize, struct TreeNode *node) {
int count = 0;
while (node != NULL) {
++count;
vec[(*vecSize)++] = node->val;
node = node->right;
}
for (int i = (*vecSize) - count, j = (*vecSize) - 1; i < j; ++i, --j) {
int t = vec[i];
vec[i] = vec[j];
vec[j] = t;
}
}
int *postorderTraversal(struct TreeNode *root, int *returnSize) {
int *res = malloc(sizeof(int) * 2001);
*returnSize = 0;
if (root == NULL) {
return res;
}
struct TreeNode *p1 = root, *p2 = NULL;
while (p1 != NULL) {
p2 = p1->left;
if (p2 != NULL) {
while (p2->right != NULL && p2->right != p1) {
p2 = p2->right;
}
if (p2->right == NULL) {
p2->right = p1;
p1 = p1->left;
continue;
} else {
p2->right = NULL;
addPath(res, returnSize, p1->left);
}
}
p1 = p1->right;
}
addPath(res, returnSize, root);
return res;
}
|
复杂度分析

 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>