0166-分数到小数

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 10:43:23 2023-09-13 10:43:23 Updated    

给定两个整数，分别表示分数的分子 numerator 和分母 denominator，以 字符串形式返回小数 。

如果小数部分为循环小数，则将循环的部分括在括号内。

如果存在多个答案，只需返回 任意一个 。

对于所有给定的输入， 保证 答案字符串的长度小于 104 。

示例 1：

**输入：** numerator = 1, denominator = 2
**输出：** "0.5"

示例 2：

**输入：** numerator = 2, denominator = 1
**输出：** "2"

示例 3：

**输入：** numerator = 4, denominator = 333
**输出：** "0.(012)"

提示：

  • -231 <= numerator, denominator <= 231 - 1
  • denominator != 0

方法一：长除法

题目要求根据给定的分子和分母，将分数转成整数或小数。由于给定的分子和分母的取值范围都是 $[-2^{31}, 2^{31}-1]$，为了防止计算过程中产生溢出，需要将分子和分母转成 $64$ 位整数表示。

将分数转成整数或小数，做法是计算分子和分母相除的结果。可能的结果有三种：整数、有限小数、无限循环小数。

如果分子可以被分母整除，则结果是整数，将分子除以分母的商以字符串的形式返回即可。

如果分子不能被分母整除，则结果是有限小数或无限循环小数，需要通过模拟长除法的方式计算结果。为了方便处理，首先根据分子和分母的正负决定结果的正负（注意此时分子和分母都不为 $0$），然后将分子和分母都转成正数，再计算长除法。

计算长除法时，首先计算结果的整数部分，将以下部分依次拼接到结果中：

  1. 如果结果是负数则将负号拼接到结果中，如果结果是正数则跳过这一步；

  2. 将整数部分拼接到结果中；

  3. 将小数点拼接到结果中。

完成上述拼接之后，根据余数计算小数部分。

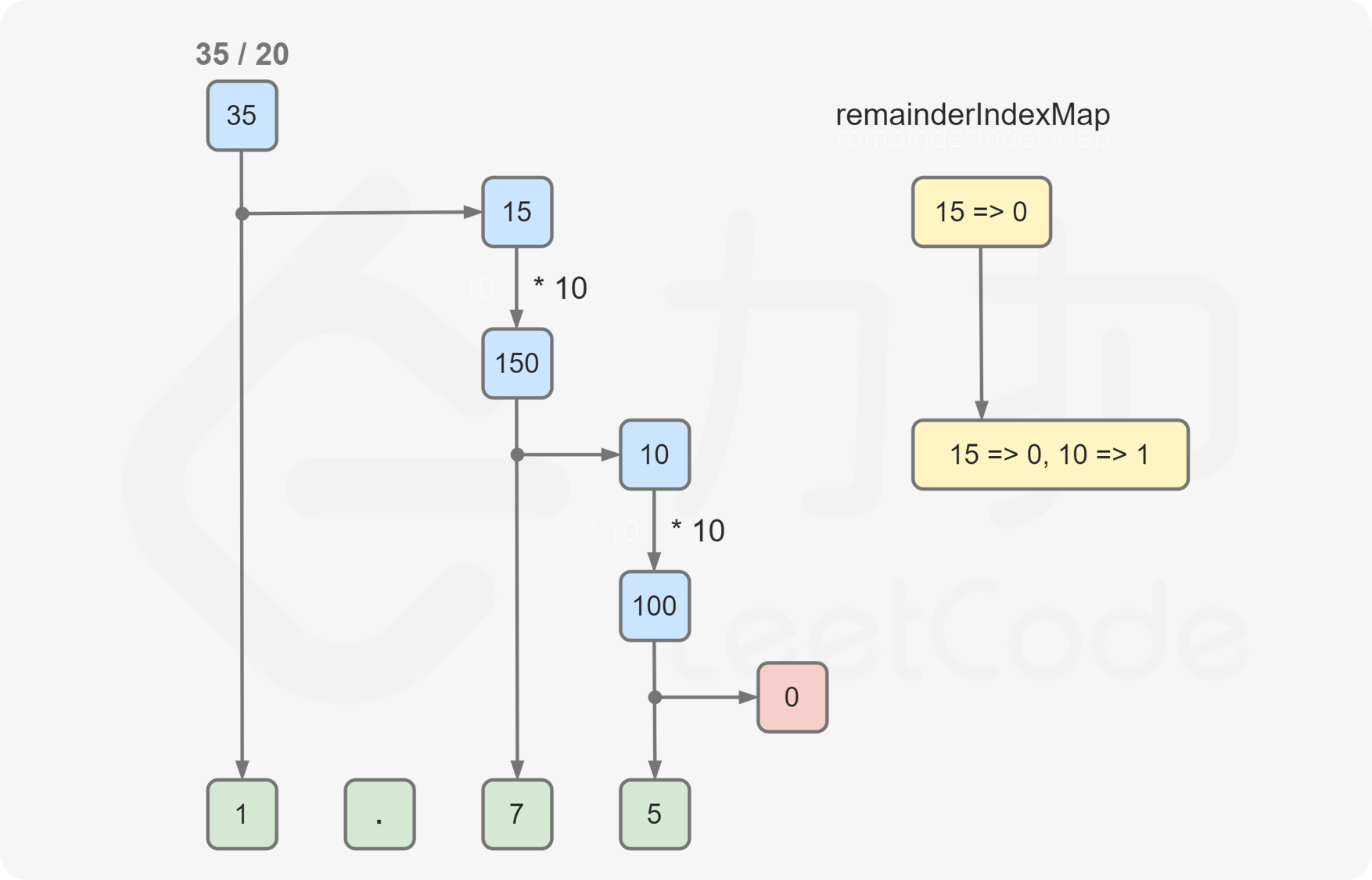
计算小数部分时，每次将余数乘以 $10$，然后计算小数的下一位数字，并得到新的余数。重复上述操作直到余数变成 $0$ 或者找到循环节。

  • 如果余数变成 $0$，则结果是有限小数，将小数部分拼接到结果中。

  • 如果找到循环节，则找到循环节的开始位置和结束位置并加上括号，然后将小数部分拼接到结果中。

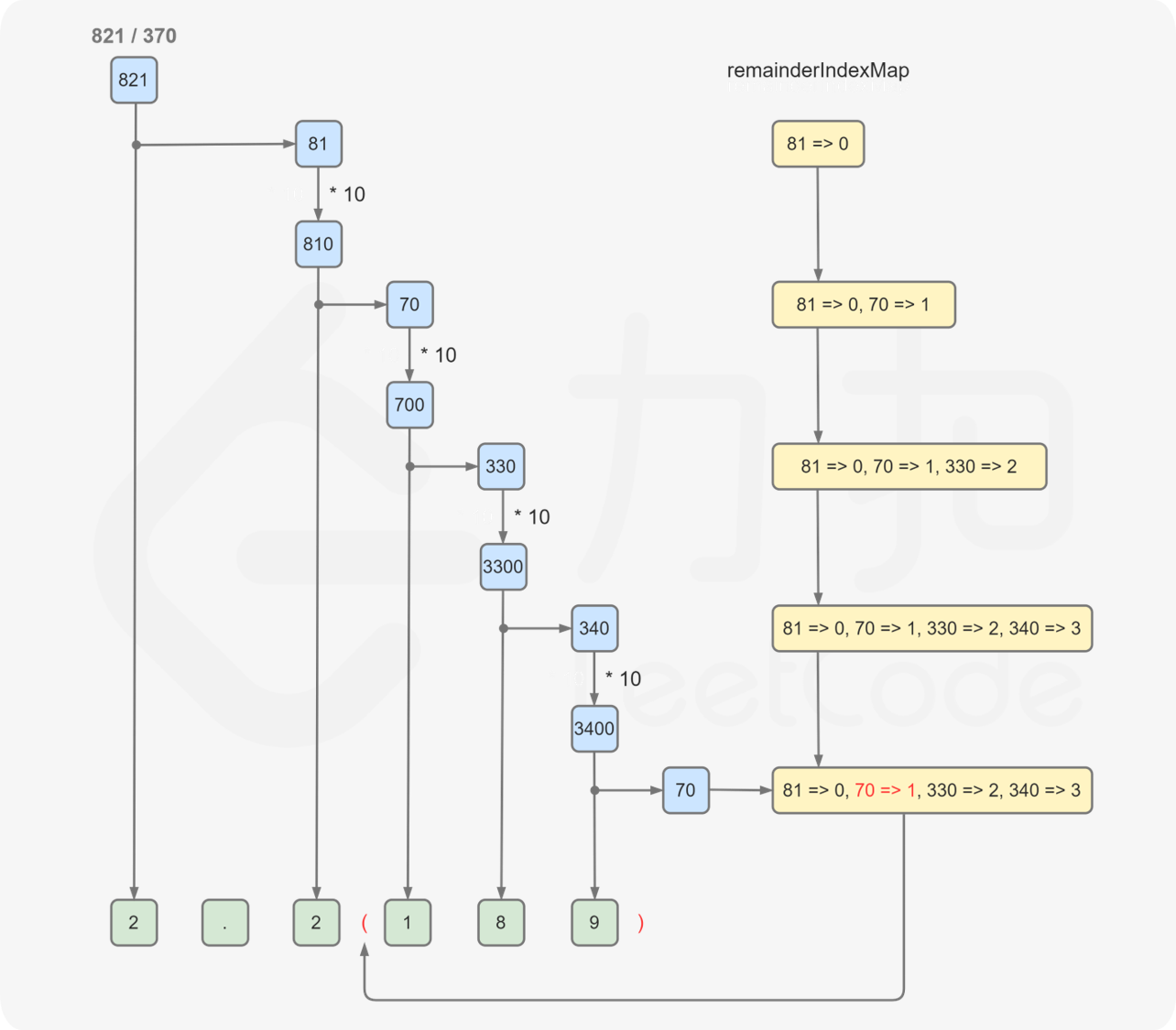
如何判断是否找到循环节？注意到对于相同的余数，计算得到的小数的下一位数字一定是相同的，因此如果计算过程中发现某一位的余数在之前已经出现过，则为找到循环节。为了记录每个余数是否已经出现过，需要使用哈希表存储每个余数在小数部分第一次出现的下标。

假设在计算小数部分的第 $i$ 位之前，余数为 $\textit{remainder}i$，则在计算小数部分的第 $i$ 位之后，余数为 $\textit{remainder}{i+1}$。

假设存在下标 $j$ 和 $k$，满足 $j \le k$ 且 $\textit{remainder}j = \textit{remainder}{k+1}$，则小数部分的第 $k+1$ 位和小数部分的第 $j$ 位相同，因此小数部分的第 $j$ 位到第 $k$ 位是一个循环节。在计算小数部分的第 $k$ 位之后就会发现这个循环节的存在，因此在小数部分的第 $j$ 位之前加上左括号，在小数部分的末尾（即第 $k$ 位之后）加上右括号。

fig1

fig2

[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
    public String fractionToDecimal(int numerator, int denominator) {
        long numeratorLong = (long) numerator;
        long denominatorLong = (long) denominator;
        if (numeratorLong % denominatorLong == 0) {
            return String.valueOf(numeratorLong / denominatorLong);
        }

        StringBuffer sb = new StringBuffer();
        if (numeratorLong < 0 ^ denominatorLong < 0) {
            sb.append('-');
        }

        // 整数部分
        numeratorLong = Math.abs(numeratorLong);
        denominatorLong = Math.abs(denominatorLong);
        long integerPart = numeratorLong / denominatorLong;
        sb.append(integerPart);
        sb.append('.');

        // 小数部分
        StringBuffer fractionPart = new StringBuffer();
        Map<Long, Integer> remainderIndexMap = new HashMap<Long, Integer>();
        long remainder = numeratorLong % denominatorLong;
        int index = 0;
        while (remainder != 0 && !remainderIndexMap.containsKey(remainder)) {
            remainderIndexMap.put(remainder, index);
            remainder *= 10;
            fractionPart.append(remainder / denominatorLong);
            remainder %= denominatorLong;
            index++;
        }
        if (remainder != 0) { // 有循环节
            int insertIndex = remainderIndexMap.get(remainder);
            fractionPart.insert(insertIndex, '(');
            fractionPart.append(')');
        }
        sb.append(fractionPart.toString());

        return sb.toString();
    }
}
[sol1-C#]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
public class Solution {
    public string FractionToDecimal(int numerator, int denominator) {
        long numeratorLong = (long) numerator;
        long denominatorLong = (long) denominator;
        if (numeratorLong % denominatorLong == 0) {
            return (numeratorLong / denominatorLong).ToString();
        }

        StringBuilder sb = new StringBuilder();
        if (numeratorLong < 0 ^ denominatorLong < 0) {
            sb.Append('-');
        }

        // 整数部分
        numeratorLong = Math.Abs(numeratorLong);
        denominatorLong = Math.Abs(denominatorLong);
        long integerPart = numeratorLong / denominatorLong;
        sb.Append(integerPart);
        sb.Append('.');

        // 小数部分
        StringBuilder fractionPart = new StringBuilder();
        Dictionary<long, int> remainderIndexDic = new Dictionary<long, int>();
        long remainder = numeratorLong % denominatorLong;
        int index = 0;
        while (remainder != 0 && !remainderIndexDic.ContainsKey(remainder)) {
            remainderIndexDic.Add(remainder, index);
            remainder *= 10;
            fractionPart.Append(remainder / denominatorLong);
            remainder %= denominatorLong;
            index++;
        }
        if (remainder != 0) { // 有循环节
            int insertIndex = remainderIndexDic[remainder];
            fractionPart.Insert(insertIndex, '(');
            fractionPart.Append(')');
        }
        sb.Append(fractionPart.ToString());

        return sb.ToString();
    }
}
[sol1-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
var fractionToDecimal = function(numerator, denominator) {
    if (numerator % denominator == 0) {
        return '' + Math.floor(numerator / denominator);
    }

    const sb = [];
    if (numerator < 0 ^ denominator < 0) {
        sb.push('-');
    }

    // 整数部分
    numerator = Math.abs(numerator);
    denominator = Math.abs(denominator);
    const integerPart = Math.floor(numerator / denominator);
    sb.push(integerPart);
    sb.push('.');

    // 小数部分
    const fractionPart = [];
    const remainderIndexDic = new Map();
    let remainder = numerator % denominator;
    let index = 0;
    while (remainder !== 0 && !remainderIndexDic.has(remainder)) {
        remainderIndexDic.set(remainder, index);
        remainder *= 10;
        fractionPart.push(Math.floor(remainder / denominator));
        remainder %= denominator;
        index++;
    }
    if (remainder !== 0) { // 有循环节
        let insertIndex = remainderIndexDic.get(remainder);
        fractionPart.splice(insertIndex, 0, '(');
        fractionPart.push(')');
    }
    sb.push(fractionPart.join(''));

    return sb.join('');
}
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
func fractionToDecimal(numerator, denominator int) string {
    if numerator%denominator == 0 {
        return strconv.Itoa(numerator / denominator)
    }

    s := []byte{}
    if numerator < 0 != (denominator < 0) {
        s = append(s, '-')
    }

    // 整数部分
    numerator = abs(numerator)
    denominator = abs(denominator)
    integerPart := numerator / denominator
    s = append(s, strconv.Itoa(integerPart)...)
    s = append(s, '.')

    // 小数部分
    indexMap := map[int]int{}
    remainder := numerator % denominator
    for remainder != 0 && indexMap[remainder] == 0 {
        indexMap[remainder] = len(s)
        remainder *= 10
        s = append(s, '0'+byte(remainder/denominator))
        remainder %= denominator
    }
    if remainder > 0 { // 有循环节
        insertIndex := indexMap[remainder]
        s = append(s[:insertIndex], append([]byte{'('}, s[insertIndex:]...)...)
        s = append(s, ')')
    }

    return string(s)
}

func abs(x int) int {
    if x < 0 {
        return -x
    }
    return x
}
[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {
public:
    string fractionToDecimal(int numerator, int denominator) {
        long numeratorLong = numerator;
        long denominatorLong = denominator;
        if (numeratorLong % denominatorLong == 0) {
            return to_string(numeratorLong / denominatorLong);
        }

        string ans;
        if (numeratorLong < 0 ^ denominatorLong < 0) {
            ans.push_back('-');
        }

        // 整数部分
        numeratorLong = abs(numeratorLong);
        denominatorLong = abs(denominatorLong);
        long integerPart = numeratorLong / denominatorLong;
        ans += to_string(integerPart);
        ans.push_back('.');

        // 小数部分
        string fractionPart;
        unordered_map<long, int> remainderIndexMap;
        long remainder = numeratorLong % denominatorLong;
        int index = 0;
        while (remainder != 0 && !remainderIndexMap.count(remainder)) {
            remainderIndexMap[remainder] = index;
            remainder *= 10;
            fractionPart += to_string(remainder / denominatorLong);
            remainder %= denominatorLong;
            index++;
        }
        if (remainder != 0) { // 有循环节
            int insertIndex = remainderIndexMap[remainder];
            fractionPart = fractionPart.substr(0,insertIndex) + '(' + fractionPart.substr(insertIndex);
            fractionPart.push_back(')');
        }
        ans += fractionPart;

        return ans;
    }
};
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution:
    def fractionToDecimal(self, numerator: int, denominator: int) -> str:
        if numerator % denominator == 0:
            return str(numerator // denominator)

        s = []
        if (numerator < 0) != (denominator < 0):
            s.append('-')

        # 整数部分
        numerator = abs(numerator)
        denominator = abs(denominator)
        integerPart = numerator // denominator
        s.append(str(integerPart))
        s.append('.')

        # 小数部分
        indexMap = {}
        remainder = numerator % denominator
        while remainder and remainder not in indexMap:
            indexMap[remainder] = len(s)
            remainder *= 10
            s.append(str(remainder // denominator))
            remainder %= denominator
        if remainder:  # 有循环节
            insertIndex = indexMap[remainder]
            s.insert(insertIndex, '(')
            s.append(')')

        return ''.join(s)

复杂度分析

  • 时间复杂度：$O(l)$，其中 $l$ 是答案字符串的长度，这道题中 $l \le 10^4$。对于答案字符串中的每一个字符，计算时间都是 $O(1)$。

  • 空间复杂度：$O(l)$，其中 $l$ 是答案字符串的长度，这道题中 $l \le 10^4$。空间复杂度主要取决于答案字符串和哈希表，哈希表中的每个键值对所对应的下标各不相同，因此键值对的数量不会超过 $l$。

 Comments
On this page
0166-分数到小数