0169-多数元素
给定一个大小为 n __ 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
**输入:** nums = [3,2,3]
**输出:** 3
示例 2:
**输入:** nums = [2,2,1,1,1,2,2]
**输出:** 2
提示:
n == nums.length1 <= n <= 5 * 104-109 <= nums[i] <= 109
进阶: 尝试设计时间复杂度为 O(n)、空间复杂度为 O(1) 的算法解决此问题。
说明
最简单的暴力方法是,枚举数组中的每个元素,再遍历一遍数组统计其出现次数。该方法的时间复杂度是 $O(n^2)$,会超出时间限制,因此我们需要找出时间复杂度小于 $O(n^2)$ 的优秀做法。
方法一:哈希表
思路
我们知道出现次数最多的元素大于 $\lfloor \dfrac{n}{2} \rfloor$ 次,所以可以用哈希表来快速统计每个元素出现的次数。
算法
我们使用哈希映射(HashMap)来存储每个元素以及出现的次数。对于哈希映射中的每个键值对,键表示一个元素,值表示该元素出现的次数。
我们用一个循环遍历数组 nums 并将数组中的每个元素加入哈希映射中。在这之后,我们遍历哈希映射中的所有键值对,返回值最大的键。我们同样也可以在遍历数组 nums 时候使用打擂台的方法,维护最大的值,这样省去了最后对哈希映射的遍历。
1 | class Solution { |
1 | class Solution: |
1 | class Solution { |
复杂度分析
时间复杂度:$O(n)$,其中 $n$ 是数组
nums的长度。我们遍历数组nums一次,对于nums中的每一个元素,将其插入哈希表都只需要常数时间。如果在遍历时没有维护最大值,在遍历结束后还需要对哈希表进行遍历,因为哈希表中占用的空间为 $O(n)$(可参考下文的空间复杂度分析),那么遍历的时间不会超过 $O(n)$。因此总时间复杂度为 $O(n)$。空间复杂度:$O(n)$。哈希表最多包含 $n - \lfloor \dfrac{n}{2} \rfloor$ 个键值对,所以占用的空间为 $O(n)$。这是因为任意一个长度为 $n$ 的数组最多只能包含 $n$ 个不同的值,但题中保证
nums一定有一个众数,会占用(最少) $\lfloor \dfrac{n}{2} \rfloor + 1$ 个数字。因此最多有 $n - (\lfloor \dfrac{n}{2} \rfloor + 1)$ 个不同的其他数字,所以最多有 $n - \lfloor \dfrac{n}{2} \rfloor$ 个不同的元素。
方法二:排序
思路
如果将数组 nums 中的所有元素按照单调递增或单调递减的顺序排序,那么下标为 $\lfloor \dfrac{n}{2} \rfloor$ 的元素(下标从 0 开始)一定是众数。
算法
对于这种算法,我们先将 nums 数组排序,然后返回上文所说的下标对应的元素。下面的图中解释了为什么这种策略是有效的。在下图中,第一个例子是 $n$ 为奇数的情况,第二个例子是 $n$ 为偶数的情况。
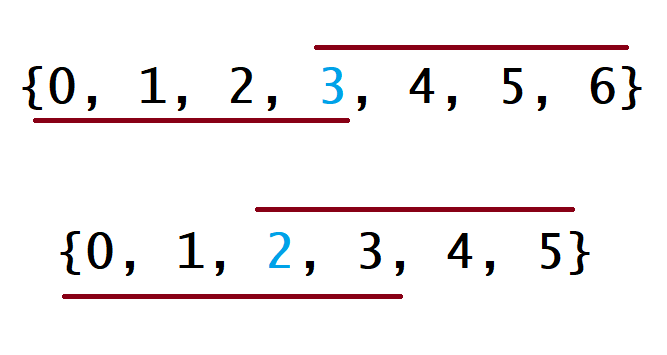 {:width=”200px”}
{:width=”200px”}
对于每种情况,数组上面的线表示如果众数是数组中的最小值时覆盖的下标,数组下面的线表示如果众数是数组中的最大值时覆盖的下标。对于其他的情况,这条线会在这两种极端情况的中间。对于这两种极端情况,它们会在下标为 $\lfloor \dfrac{n}{2} \rfloor$ 的地方有重叠。因此,无论众数是多少,返回 $\lfloor \dfrac{n}{2} \rfloor$ 下标对应的值都是正确的。
1 | class Solution { |
1 | class Solution: |
1 | class Solution { |
复杂度分析
时间复杂度:$O(n\log n)$。将数组排序的时间复杂度为 $O(n\log n)$。
空间复杂度:$O(\log n)$。如果使用语言自带的排序算法,需要使用 $O(\log n)$ 的栈空间。如果自己编写堆排序,则只需要使用 $O(1)$ 的额外空间。
方法三:随机化
思路
因为超过 $\lfloor \dfrac{n}{2} \rfloor$ 的数组下标被众数占据了,这样我们随机挑选一个下标对应的元素并验证,有很大的概率能找到众数。
算法
由于一个给定的下标对应的数字很有可能是众数,我们随机挑选一个下标,检查它是否是众数,如果是就返回,否则继续随机挑选。
1 | class Solution { |
1 | class Solution: |
1 | class Solution { |
复杂度分析
时间复杂度:理论上最坏情况下的时间复杂度为 $O(\infty)$,因为如果我们的运气很差,这个算法会一直找不到众数,随机挑选无穷多次,所以最坏时间复杂度是没有上限的。然而,运行的期望时间是线性的。为了更简单地分析,先说服你自己:由于众数占据 超过 数组一半的位置,期望的随机次数会小于众数占据数组恰好一半的情况。因此,我们可以计算随机的期望次数(下标为
prob为原问题,mod为众数恰好占据数组一半数目的问题):$$
\begin{aligned}
E(\textit{iters}{prob}) &\leq E(\textit{iters}{mod}) \
&= \lim_{n\to\infty} \sum_{i=1}^{n} i \cdot \frac{1}{2^i} \
&= 2
\end{aligned}
$$计算方法为:当众数恰好占据数组的一半时,第一次随机我们有 $\frac{1}{2}$ 的概率找到众数,如果没有找到,则第二次随机时,包含上一次我们有 $\frac{1}{4}$ 的概率找到众数,以此类推。因此期望的次数为 $i * \frac{1}{2^i}$ 的和,可以计算出这个和为 $2$,说明期望的随机次数是常数。每一次随机后,我们需要 $O(n)$ 的时间判断这个数是否为众数,因此期望的时间复杂度为 $O(n)$。
空间复杂度:$O(1)$。随机方法只需要常数级别的额外空间。
方法四:分治
思路
如果数 a 是数组 nums 的众数,如果我们将 nums 分成两部分,那么 a 必定是至少一部分的众数。
我们可以使用反证法来证明这个结论。假设 a 既不是左半部分的众数,也不是右半部分的众数,那么 a 出现的次数少于 l / 2 + r / 2 次,其中 l 和 r 分别是左半部分和右半部分的长度。由于 l / 2 + r / 2 <= (l + r) / 2,说明 a 也不是数组 nums 的众数,因此出现了矛盾。所以这个结论是正确的。
这样以来,我们就可以使用分治法解决这个问题:将数组分成左右两部分,分别求出左半部分的众数 a1 以及右半部分的众数 a2,随后在 a1 和 a2 中选出正确的众数。
算法
我们使用经典的分治算法递归求解,直到所有的子问题都是长度为 1 的数组。长度为 1 的子数组中唯一的数显然是众数,直接返回即可。如果回溯后某区间的长度大于 1,我们必须将左右子区间的值合并。如果它们的众数相同,那么显然这一段区间的众数是它们相同的值。否则,我们需要比较两个众数在整个区间内出现的次数来决定该区间的众数。
1 | class Solution { |
1 | class Solution: |
1 | class Solution { |
复杂度分析
时间复杂度:$O(n\log n)$。函数
majority_element_rec()会求解 2 个长度为 $\dfrac{n}{2}$ 的子问题,并做两遍长度为 $n$ 的线性扫描。因此,分治算法的时间复杂度可以表示为:$$
T(n) = 2T(\frac{n}{2}) + 2n
$$根据 主定理 ,本题满足第二种情况,所以时间复杂度可以表示为:
$$
\begin{aligned}
T(n) &= \Theta(n^{log_{b}a}\log n) \
&= \Theta(n^{log_{2}2}\log n) \
&= \Theta(n \log n) \
\end{aligned}
$$空间复杂度:$O(\log n)$。尽管分治算法没有直接分配额外的数组空间,但在递归的过程中使用了额外的栈空间。算法每次将数组从中间分成两部分,所以数组长度变为
1之前需要进行 $O(\log n)$ 次递归,即空间复杂度为 $O(\log n)$。
方法五:Boyer-Moore 投票算法
思路
如果我们把众数记为 $+1$,把其他数记为 $-1$,将它们全部加起来,显然和大于 0,从结果本身我们可以看出众数比其他数多。
算法
Boyer-Moore 算法的本质和方法四中的分治十分类似。我们首先给出 Boyer-Moore 算法的详细步骤:
我们维护一个候选众数
candidate和它出现的次数count。初始时candidate可以为任意值,count为0;我们遍历数组
nums中的所有元素,对于每个元素x,在判断x之前,如果count的值为0,我们先将x的值赋予candidate,随后我们判断x:如果
x与candidate相等,那么计数器count的值增加1;如果
x与candidate不等,那么计数器count的值减少1。
在遍历完成后,
candidate即为整个数组的众数。
我们举一个具体的例子,例如下面的这个数组:
1 | [7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 7, 7, 7, 7] |
在遍历到数组中的第一个元素以及每个在 | 之后的元素时,candidate 都会因为 count 的值变为 0 而发生改变。最后一次 candidate 的值从 5 变为 7,也就是这个数组中的众数。
Boyer-Moore 算法的正确性较难证明,这里给出一种较为详细的用例子辅助证明的思路,供读者参考:
首先我们根据算法步骤中对 count 的定义,可以发现:在对整个数组进行遍历的过程中,count 的值一定非负。这是因为如果 count 的值为 0,那么在这一轮遍历的开始时刻,我们会将 x 的值赋予 candidate 并在接下来的一步中将 count 的值增加 1。因此 count 的值在遍历的过程中一直保持非负。
那么 count 本身除了计数器之外,还有什么更深层次的意义呢?我们还是以数组
1 | [7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 7, 7, 7, 7] |
作为例子,首先写下它在每一步遍历时 candidate 和 count 的值:
1 | nums: [7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 7, 7, 7, 7] |
我们再定义一个变量 value,它和真正的众数 maj 绑定。在每一步遍历时,如果当前的数 x 和 maj 相等,那么 value 的值加 1,否则减 1。value 的实际意义即为:到当前的这一步遍历为止,众数出现的次数比非众数多出了多少次。我们将 value 的值也写在下方:
1 | nums: [7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 7, 7, 7, 7] |
有没有发现什么?我们将 count 和 value 放在一起:
1 | nums: [7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 7, 7, 7, 7] |
发现在每一步遍历中,count 和 value 要么相等,要么互为相反数!并且在候选众数 candidate 就是 maj 时,它们相等,candidate 是其它的数时,它们互为相反数!
为什么会有这么奇妙的性质呢?这并不难证明:我们将候选众数 candidate 保持不变的连续的遍历称为「一段」。在同一段中,count 的值是根据 candidate == x 的判断进行加减的。那么如果 candidate 恰好为 maj,那么在这一段中,count 和 value 的变化是同步的;如果 candidate 不为 maj,那么在这一段中 count 和 value 的变化是相反的。因此就有了这样一个奇妙的性质。
这样以来,由于:
我们证明了
count的值一直为非负,在最后一步遍历结束后也是如此;由于
value的值与真正的众数maj绑定,并且它表示「众数出现的次数比非众数多出了多少次」,那么在最后一步遍历结束后,value的值为正数;
在最后一步遍历结束后,count 非负,value 为正数,所以它们不可能互为相反数,只可能相等,即 count == value。因此在最后「一段」中,count 的 value 的变化是同步的,也就是说,candidate 中存储的候选众数就是真正的众数 maj。
1 | class Solution { |
1 | class Solution: |
1 | class Solution { |
复杂度分析
时间复杂度:$O(n)$。Boyer-Moore 算法只对数组进行了一次遍历。
空间复杂度:$O(1)$。Boyer-Moore 算法只需要常数级别的额外空间。