颠倒给定的 32 位无符号整数的二进制位。
提示:
- 请注意,在某些语言(如 Java)中,没有无符号整数类型。在这种情况下,输入和输出都将被指定为有符号整数类型,并且不应影响您的实现,因为无论整数是有符号的还是无符号的,其内部的二进制表示形式都是相同的。
- 在 Java 中,编译器使用二进制补码 记法来表示有符号整数。因此,在 示例 2 中,输入表示有符号整数
-3,输出表示有符号整数 -1073741825。
示例 1:
**输入:** n = 00000010100101000001111010011100
**输出:** 964176192 (00111001011110000010100101000000)
**解释:** 输入的二进制串 **00000010100101000001111010011100** 表示无符号整数 **43261596** **,** 因此返回 964176192,其二进制表示形式为 **00111001011110000010100101000000** 。
示例 2:
**输入:** n = 11111111111111111111111111111101
**输出:** 3221225471 (10111111111111111111111111111111)
**解释:** 输入的二进制串 **11111111111111111111111111111101** 表示无符号整数 4294967293,
因此返回 3221225471 其二进制表示形式为 **10111111111111111111111111111111 。**
提示:
进阶 : 如果多次调用这个函数,你将如何优化你的算法?
方法一:逐位颠倒
思路
将 $n$ 视作一个长为 $32$ 的二进制串,从低位往高位枚举 $n$ 的每一位,将其倒序添加到翻转结果 $\textit{rev}$ 中。
代码实现中,每枚举一位就将 $n$ 右移一位,这样当前 $n$ 的最低位就是我们要枚举的比特位。当 $n$ 为 $0$ 时即可结束循环。
需要注意的是,在某些语言(如 $\texttt{Java}$)中,没有无符号整数类型,因此对 $n$ 的右移操作应使用逻辑右移。
代码
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
| class Solution {
public:
uint32_t reverseBits(uint32_t n) {
uint32_t rev = 0;
for (int i = 0; i < 32 && n > 0; ++i) {
rev |= (n & 1) << (31 - i);
n >>= 1;
}
return rev;
}
};
|
[sol1-Java]1
2
3
4
5
6
7
8
9
10
| public class Solution {
public int reverseBits(int n) {
int rev = 0;
for (int i = 0; i < 32 && n != 0; ++i) {
rev |= (n & 1) << (31 - i);
n >>>= 1;
}
return rev;
}
}
|
[sol1-Golang]1
2
3
4
5
6
7
| func reverseBits(n uint32) (rev uint32) {
for i := 0; i < 32 && n > 0; i++ {
rev |= n & 1 << (31 - i)
n >>= 1
}
return
}
|
[sol1-JavaScript]1
2
3
4
5
6
7
8
| var reverseBits = function(n) {
let rev = 0;
for (let i = 0; i < 32 && n > 0; ++i) {
rev |= (n & 1) << (31 - i);
n >>>= 1;
}
return rev >>> 0;
};
|
[sol1-C]1
2
3
4
5
6
7
8
| uint32_t reverseBits(uint32_t n) {
uint32_t rev = 0;
for (int i = 0; i < 32 && n > 0; ++i) {
rev |= (n & 1) << (31 - i);
n >>= 1;
}
return rev;
}
|
复杂度分析
时间复杂度:$O(\log n)$。
空间复杂度:$O(1)$。
方法二:位运算分治
思路
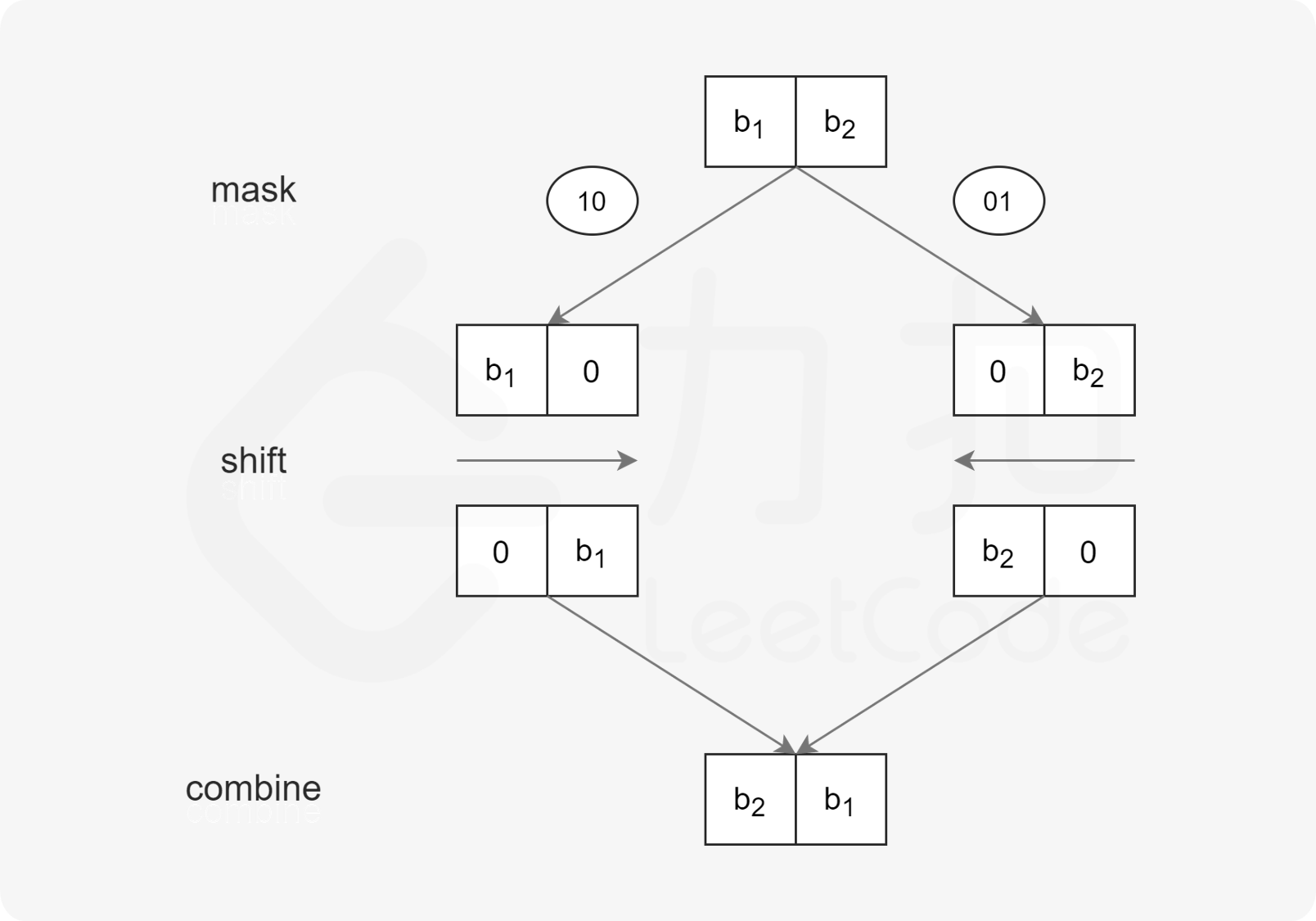
若要翻转一个二进制串,可以将其均分成左右两部分,对每部分递归执行翻转操作,然后将左半部分拼在右半部分的后面,即完成了翻转。
由于左右两部分的计算方式是相似的,利用位掩码和位移运算,我们可以自底向上地完成这一分治流程。
 {:width=”60%”}
{:width=”60%”}
对于递归的最底层,我们需要交换所有奇偶位:
- 取出所有奇数位和偶数位;
- 将奇数位移到偶数位上,偶数位移到奇数位上。
类似地,对于倒数第二层,每两位分一组,按组号取出所有奇数组和偶数组,然后将奇数组移到偶数组上,偶数组移到奇数组上。以此类推。
需要注意的是,在某些语言(如 $\texttt{Java}$)中,没有无符号整数类型,因此对 $n$ 的右移操作应使用逻辑右移。
代码
[sol2-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| class Solution {
private:
const uint32_t M1 = 0x55555555;
const uint32_t M2 = 0x33333333;
const uint32_t M4 = 0x0f0f0f0f;
const uint32_t M8 = 0x00ff00ff;
public:
uint32_t reverseBits(uint32_t n) {
n = n >> 1 & M1 | (n & M1) << 1;
n = n >> 2 & M2 | (n & M2) << 2;
n = n >> 4 & M4 | (n & M4) << 4;
n = n >> 8 & M8 | (n & M8) << 8;
return n >> 16 | n << 16;
}
};
|
[sol2-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
| public class Solution {
private static final int M1 = 0x55555555;
private static final int M2 = 0x33333333;
private static final int M4 = 0x0f0f0f0f;
private static final int M8 = 0x00ff00ff;
public int reverseBits(int n) {
n = n >>> 1 & M1 | (n & M1) << 1;
n = n >>> 2 & M2 | (n & M2) << 2;
n = n >>> 4 & M4 | (n & M4) << 4;
n = n >>> 8 & M8 | (n & M8) << 8;
return n >>> 16 | n << 16;
}
}
|
[sol2-Golang]1
2
3
4
5
6
7
8
9
10
11
12
13
14
| const (
m1 = 0x55555555
m2 = 0x33333333
m4 = 0x0f0f0f0f
m8 = 0x00ff00ff
)
func reverseBits(n uint32) uint32 {
n = n>>1&m1 | n&m1<<1
n = n>>2&m2 | n&m2<<2
n = n>>4&m4 | n&m4<<4
n = n>>8&m8 | n&m8<<8
return n>>16 | n<<16
}
|
[sol2-JavaScript]1
2
3
4
5
6
7
8
9
10
11
12
| var reverseBits = function(n) {
const M1 = 0x55555555;
const M2 = 0x33333333;
const M4 = 0x0f0f0f0f;
const M8 = 0x00ff00ff;
n = n >>> 1 & M1 | (n & M1) << 1;
n = n >>> 2 & M2 | (n & M2) << 2;
n = n >>> 4 & M4 | (n & M4) << 4;
n = n >>> 8 & M8 | (n & M8) << 8;
return (n >>> 16 | n << 16) >>> 0;
};
|
[sol2-C]1
2
3
4
5
6
7
8
9
10
11
12
| const uint32_t M1 = 0x55555555;
const uint32_t M2 = 0x33333333;
const uint32_t M4 = 0x0f0f0f0f;
const uint32_t M8 = 0x00ff00ff;
uint32_t reverseBits(uint32_t n) {
n = n >> 1 & M1 | (n & M1) << 1;
n = n >> 2 & M2 | (n & M2) << 2;
n = n >> 4 & M4 | (n & M4) << 4;
n = n >> 8 & M8 | (n & M8) << 8;
return n >> 16 | n << 16;
}
|
复杂度分析
时间复杂度:$O(1)$。
空间复杂度:$O(1)$。
 {:width=”60%”}
{:width=”60%”}