0210-课程表 II

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 10:43:54 2023-09-13 10:43:54 Updated    

现在你总共有 numCourses 门课需要选，记为 0 到 numCourses - 1。给你一个数组 prerequisites ，其中
prerequisites[i] = [ai, bi] ，表示在选修课程 ai 前 必须 先选修 bi 。

  • 例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示：[0,1] 。

返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序，你只要返回 任意一种 就可以了。如果不可能完成所有课程，返回 一个空数组 。

示例 1：

**输入：** numCourses = 2, prerequisites = [[1,0]]
**输出：** [0,1]
**解释：** 总共有 2 门课程。要学习课程 1，你需要先完成课程 0。因此，正确的课程顺序为 [0,1] 。

示例 2：

**输入：** numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
**输出：** [0,2,1,3]
**解释：** 总共有 4 门课程。要学习课程 3，你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此，一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。

示例 3：

**输入：** numCourses = 1, prerequisites = []
**输出：** [0]

提示：

  • 1 <= numCourses <= 2000
  • 0 <= prerequisites.length <= numCourses * (numCourses - 1)
  • prerequisites[i].length == 2
  • 0 <= ai, bi < numCourses
  • ai != bi
  • 所有[ai, bi] 互不相同

📺 视频题解

210. 课程表 II的.mp4

📖 文字题解

前言

本题是一道经典的「拓扑排序」问题。

给定一个包含 $n$ 个节点的有向图 $G$，我们给出它的节点编号的一种排列，如果满足：

对于图 $G$ 中的任意一条有向边 $(u, v)$，$u$ 在排列中都出现在 $v$ 的前面。

那么称该排列是图 $G$ 的「拓扑排序」。根据上述的定义，我们可以得出两个结论：

  • 如果图 $G$ 中存在环（即图 $G$ 不是「有向无环图」），那么图 $G$ 不存在拓扑排序。这是因为假设图中存在环 $x_1, x_2, \cdots, x_n, x_1$，那么 $x_1$ 在排列中必须出现在 $x_n$ 的前面，但 $x_n$ 同时也必须出现在 $x_1$ 的前面，因此不存在一个满足要求的排列，也就不存在拓扑排序；

  • 如果图 $G$ 是有向无环图，那么它的拓扑排序可能不止一种。举一个最极端的例子，如果图 $G$ 值包含 $n$ 个节点却没有任何边，那么任意一种编号的排列都可以作为拓扑排序。

有了上述的简单分析，我们就可以将本题建模成一个求拓扑排序的问题了：

  • 我们将每一门课看成一个节点；

  • 如果想要学习课程 $A$ 之前必须完成课程 $B$，那么我们从 $B$ 到 $A$ 连接一条有向边。这样以来，在拓扑排序中，$B$ 一定出现在 $A$ 的前面。

求出该图的拓扑排序，就可以得到一种符合要求的课程学习顺序。下面介绍两种求解拓扑排序的方法。

方法一：深度优先搜索

思路

我们可以将深度优先搜索的流程与拓扑排序的求解联系起来，用一个栈来存储所有已经搜索完成的节点。

对于一个节点 $u$，如果它的所有相邻节点都已经搜索完成，那么在搜索回溯到 $u$ 的时候，$u$ 本身也会变成一个已经搜索完成的节点。这里的「相邻节点」指的是从 $u$ 出发通过一条有向边可以到达的所有节点。

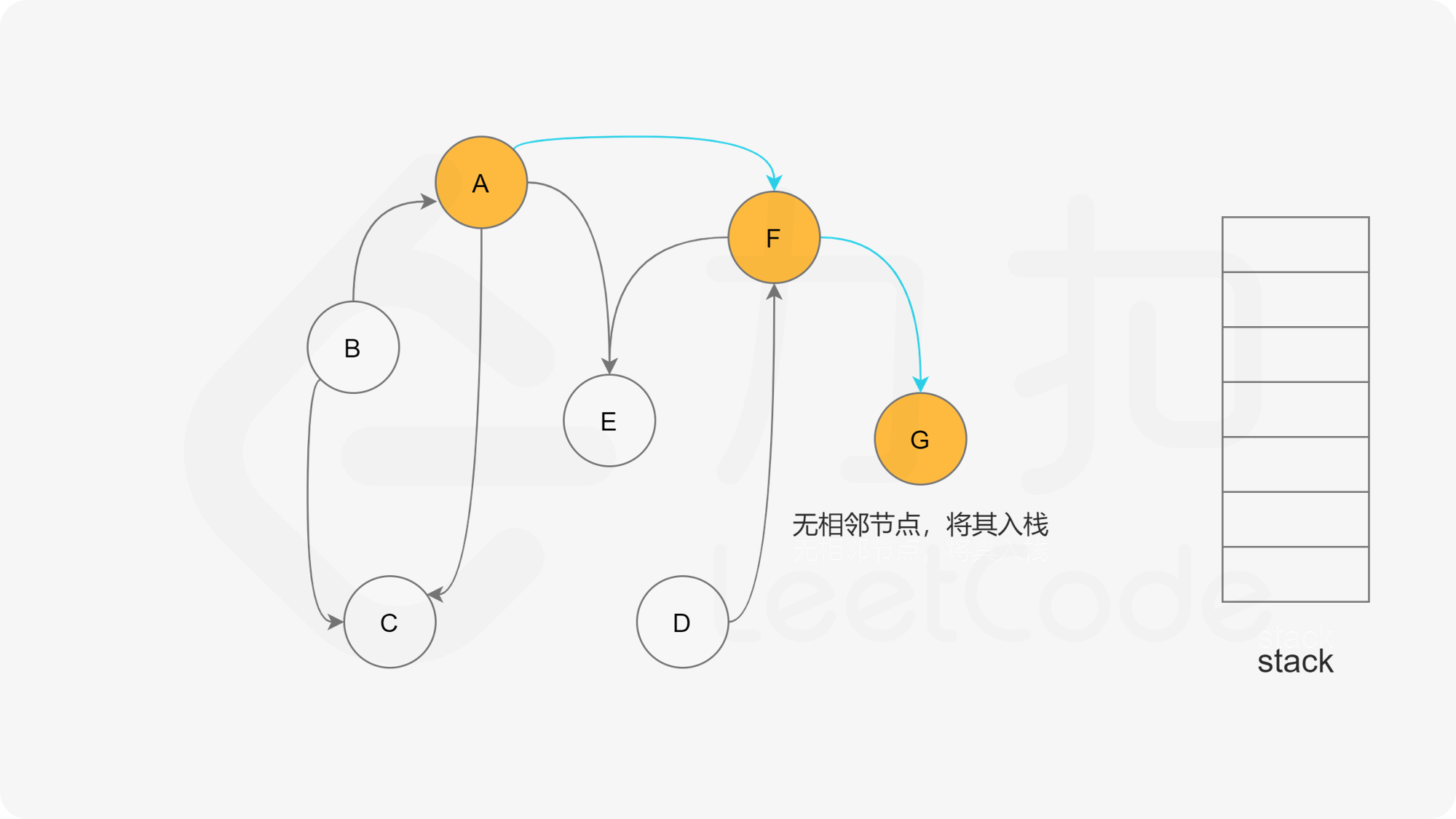
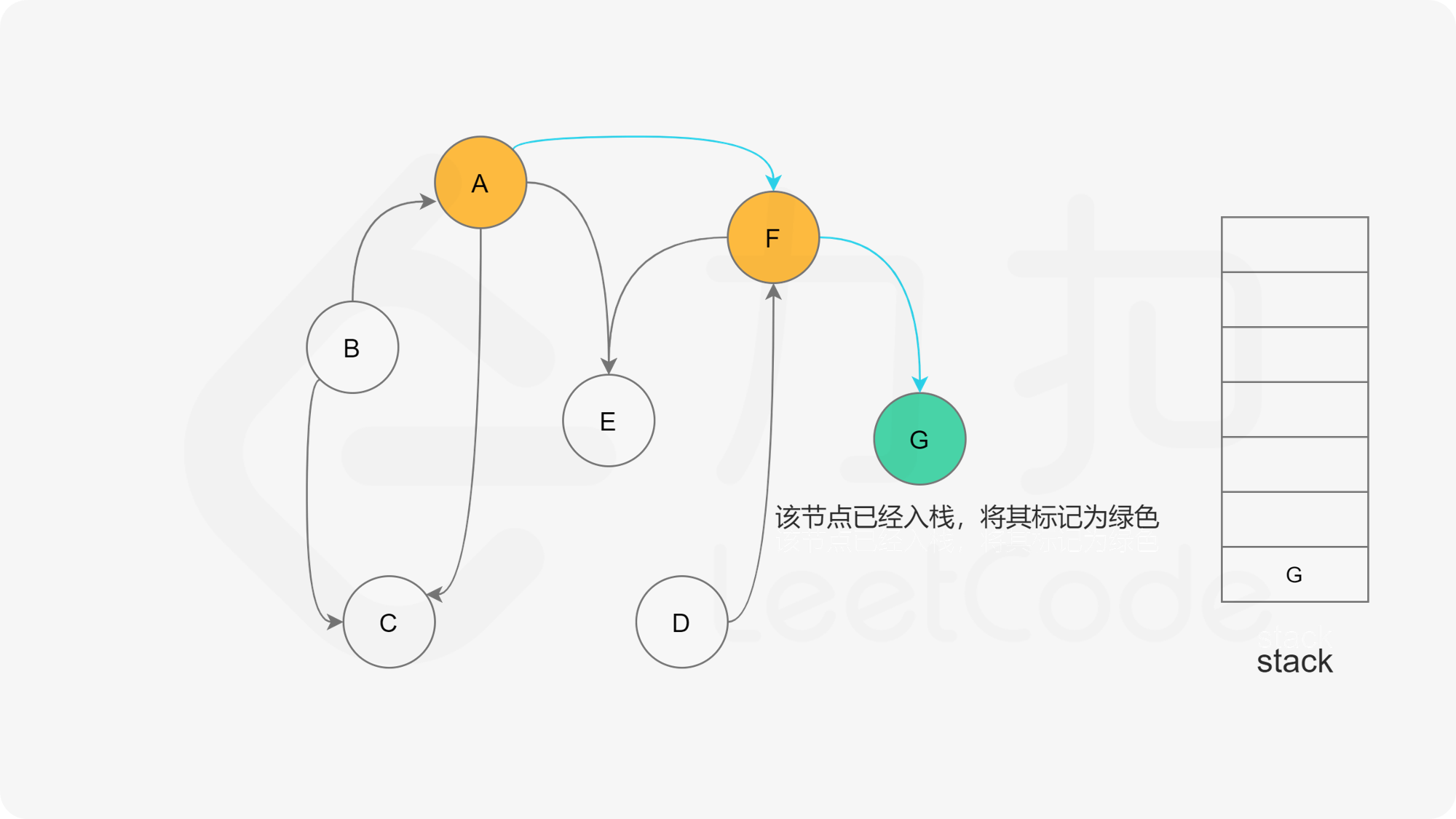
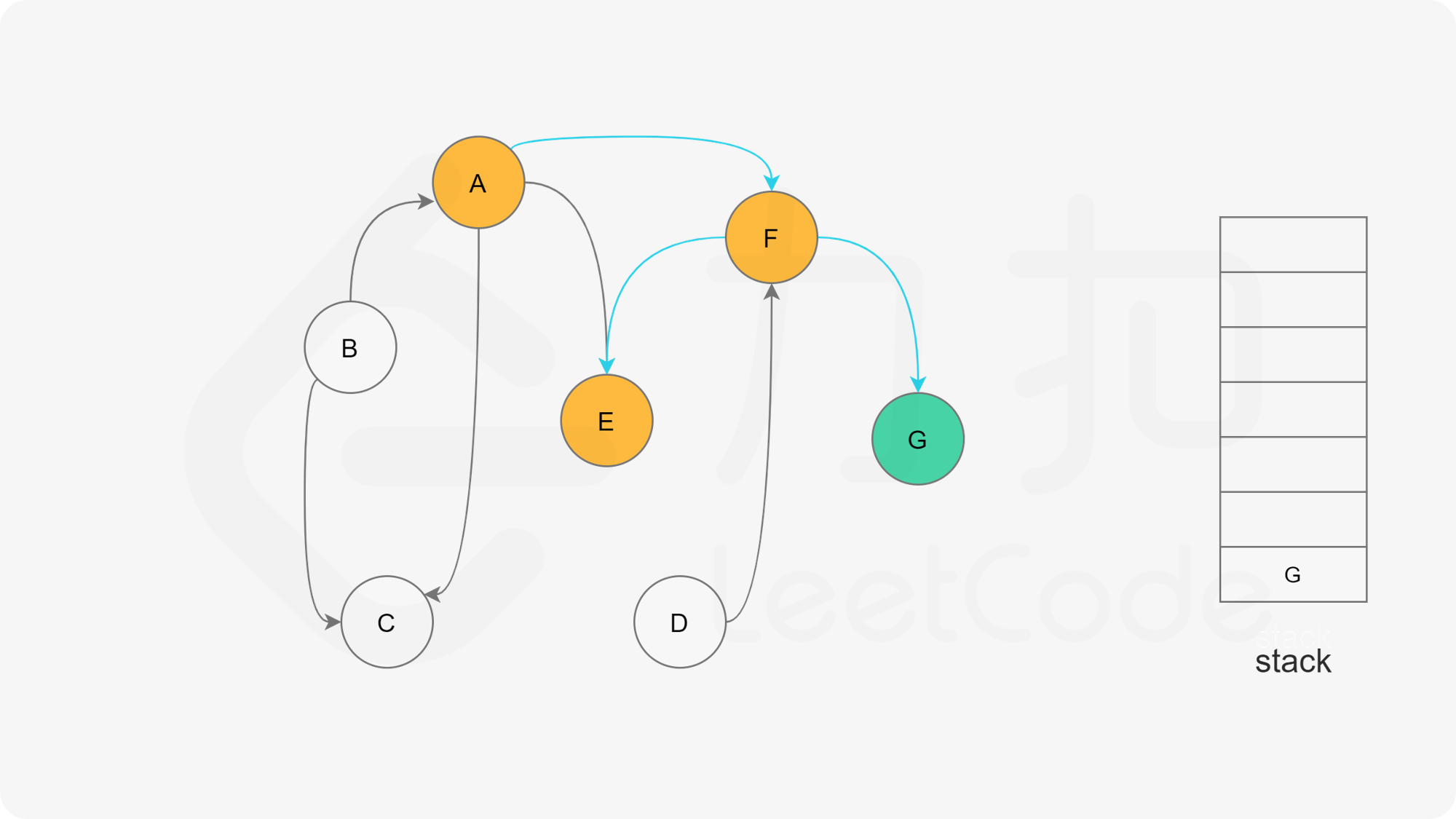
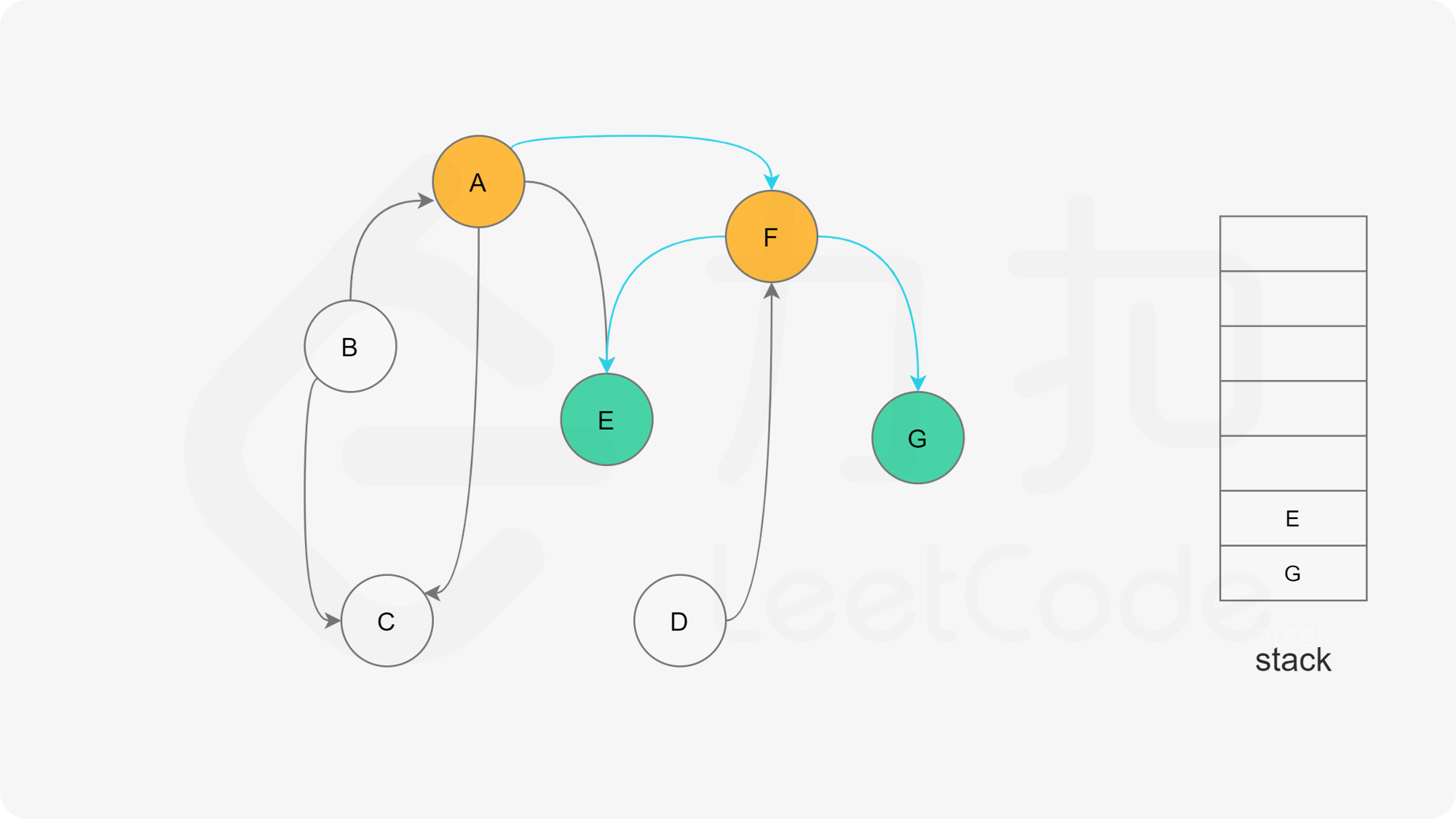
假设我们当前搜索到了节点 $u$，如果它的所有相邻节点都已经搜索完成，那么这些节点都已经在栈中了，此时我们就可以把 $u$ 入栈。可以发现，如果我们从栈顶往栈底的顺序看，由于 $u$ 处于栈顶的位置，那么 $u$ 出现在所有 $u$ 的相邻节点的前面。因此对于 $u$ 这个节点而言，它是满足拓扑排序的要求的。

这样以来，我们对图进行一遍深度优先搜索。当每个节点进行回溯的时候，我们把该节点放入栈中。最终从栈顶到栈底的序列就是一种拓扑排序。

算法

对于图中的任意一个节点，它在搜索的过程中有三种状态，即：

  • 「未搜索」：我们还没有搜索到这个节点；

  • 「搜索中」：我们搜索过这个节点，但还没有回溯到该节点，即该节点还没有入栈，还有相邻的节点没有搜索完成）；

  • 「已完成」：我们搜索过并且回溯过这个节点，即该节点已经入栈，并且所有该节点的相邻节点都出现在栈的更底部的位置，满足拓扑排序的要求。

通过上述的三种状态，我们就可以给出使用深度优先搜索得到拓扑排序的算法流程，在每一轮的搜索搜索开始时，我们任取一个「未搜索」的节点开始进行深度优先搜索。

  • 我们将当前搜索的节点 $u$ 标记为「搜索中」，遍历该节点的每一个相邻节点 $v$：

    • 如果 $v$ 为「未搜索」，那么我们开始搜索 $v$，待搜索完成回溯到 $u$；

    • 如果 $v$ 为「搜索中」，那么我们就找到了图中的一个环，因此是不存在拓扑排序的；

    • 如果 $v$ 为「已完成」，那么说明 $v$ 已经在栈中了，而 $u$ 还不在栈中，因此 $u$ 无论何时入栈都不会影响到 $(u, v)$ 之前的拓扑关系，以及不用进行任何操作。

  • 当 $u$ 的所有相邻节点都为「已完成」时，我们将 $u$ 放入栈中，并将其标记为「已完成」。

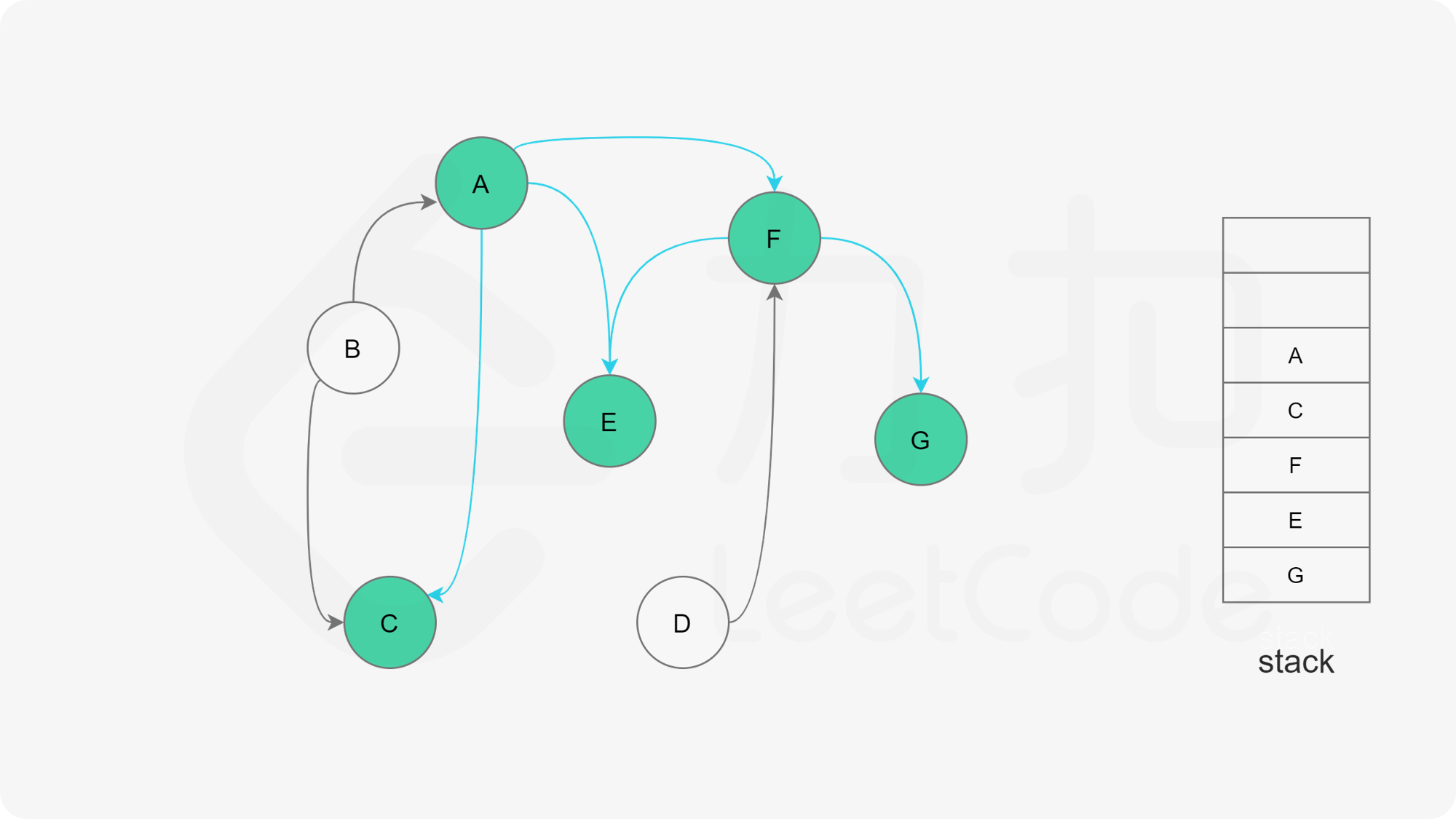
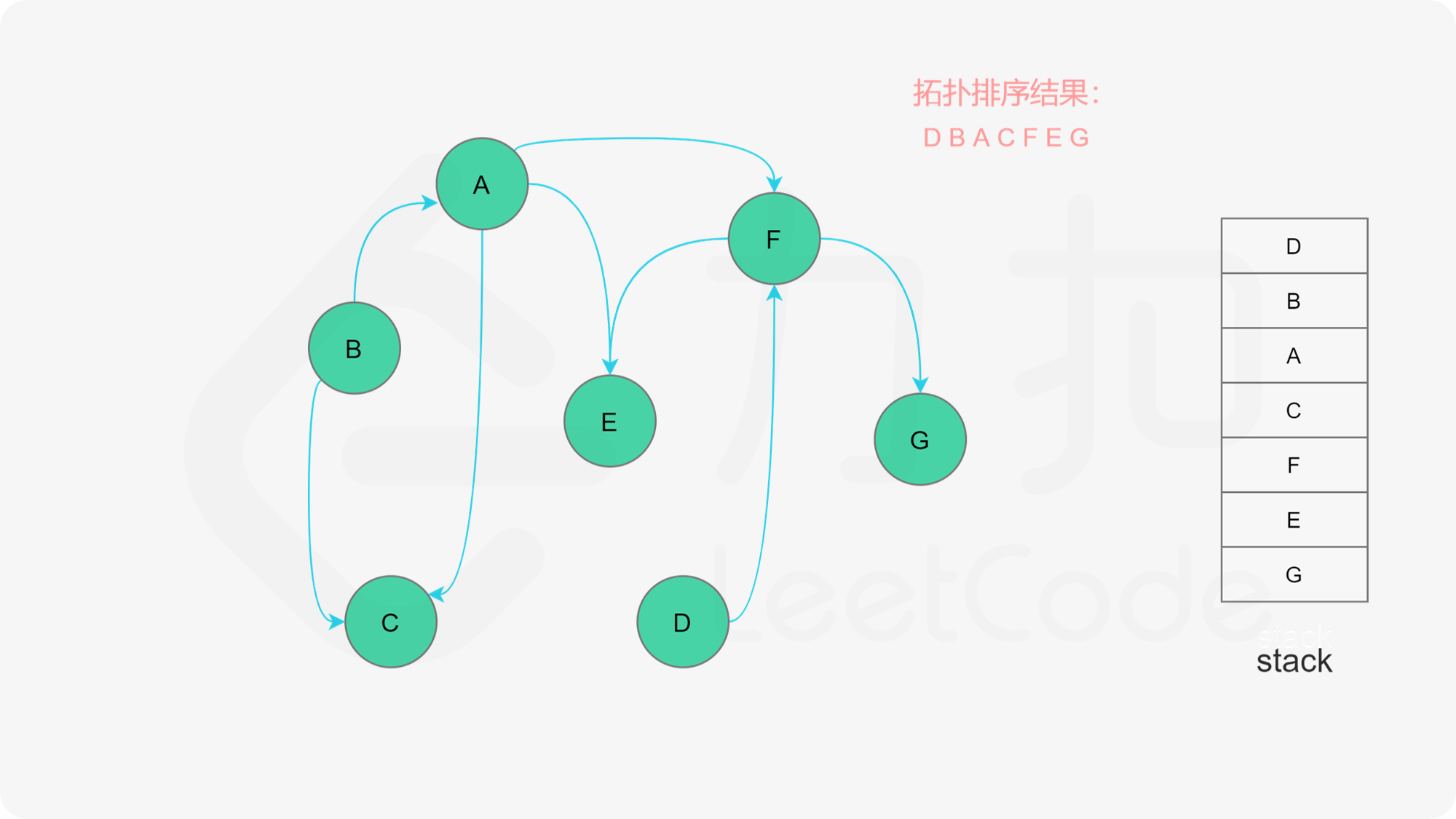
在整个深度优先搜索的过程结束后，如果我们没有找到图中的环，那么栈中存储这所有的 $n$ 个节点，从栈顶到栈底的顺序即为一种拓扑排序。

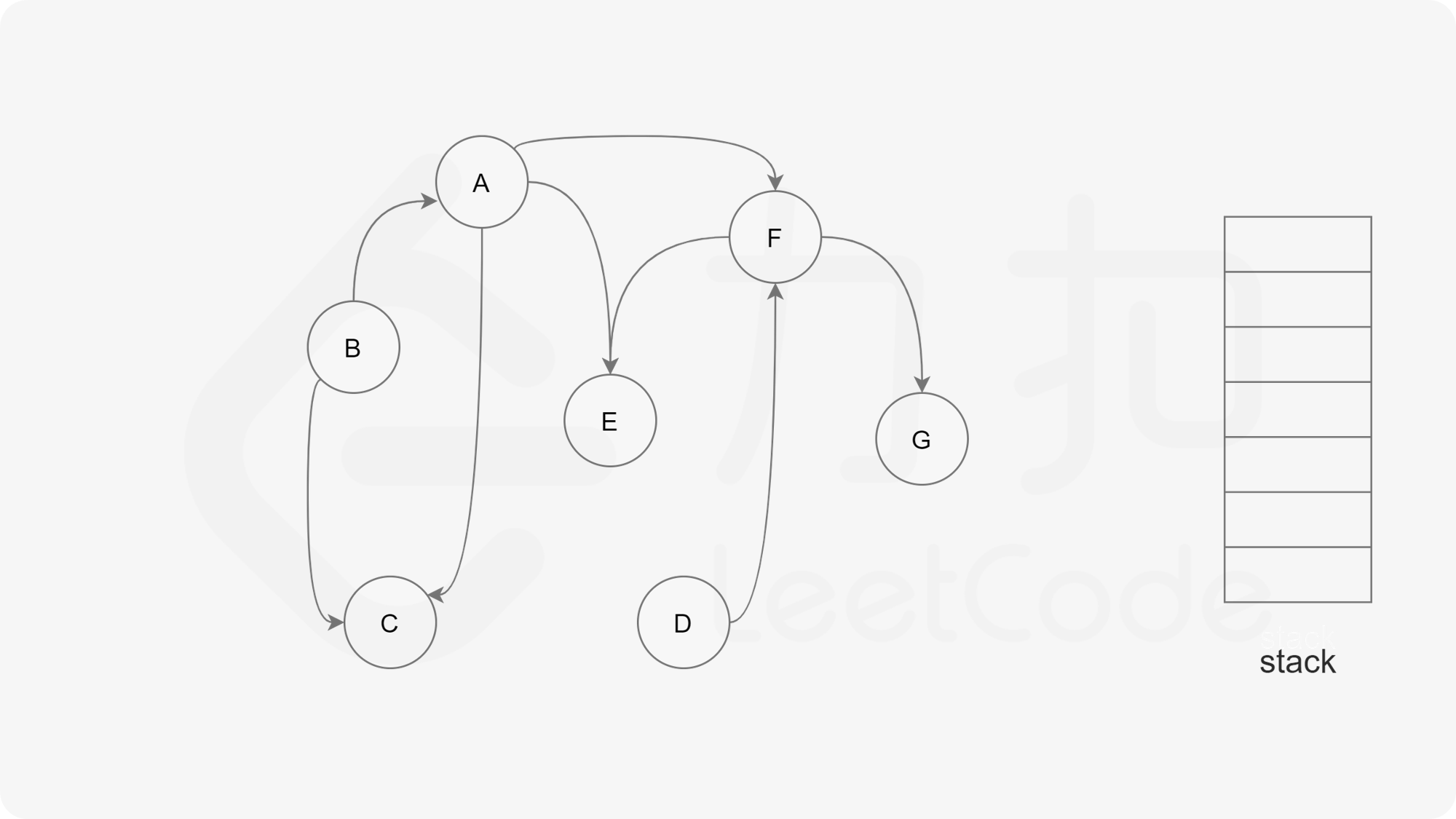
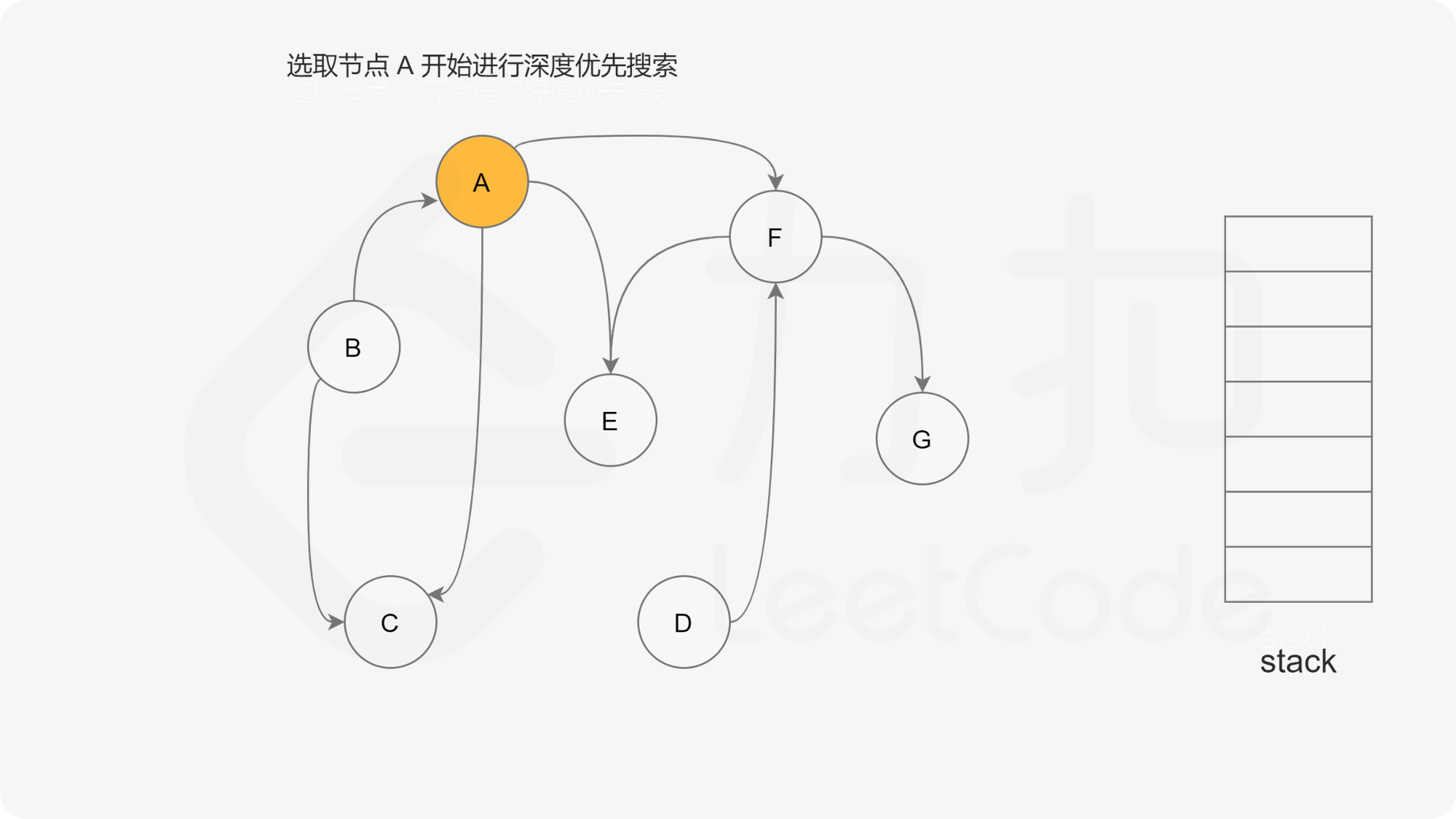
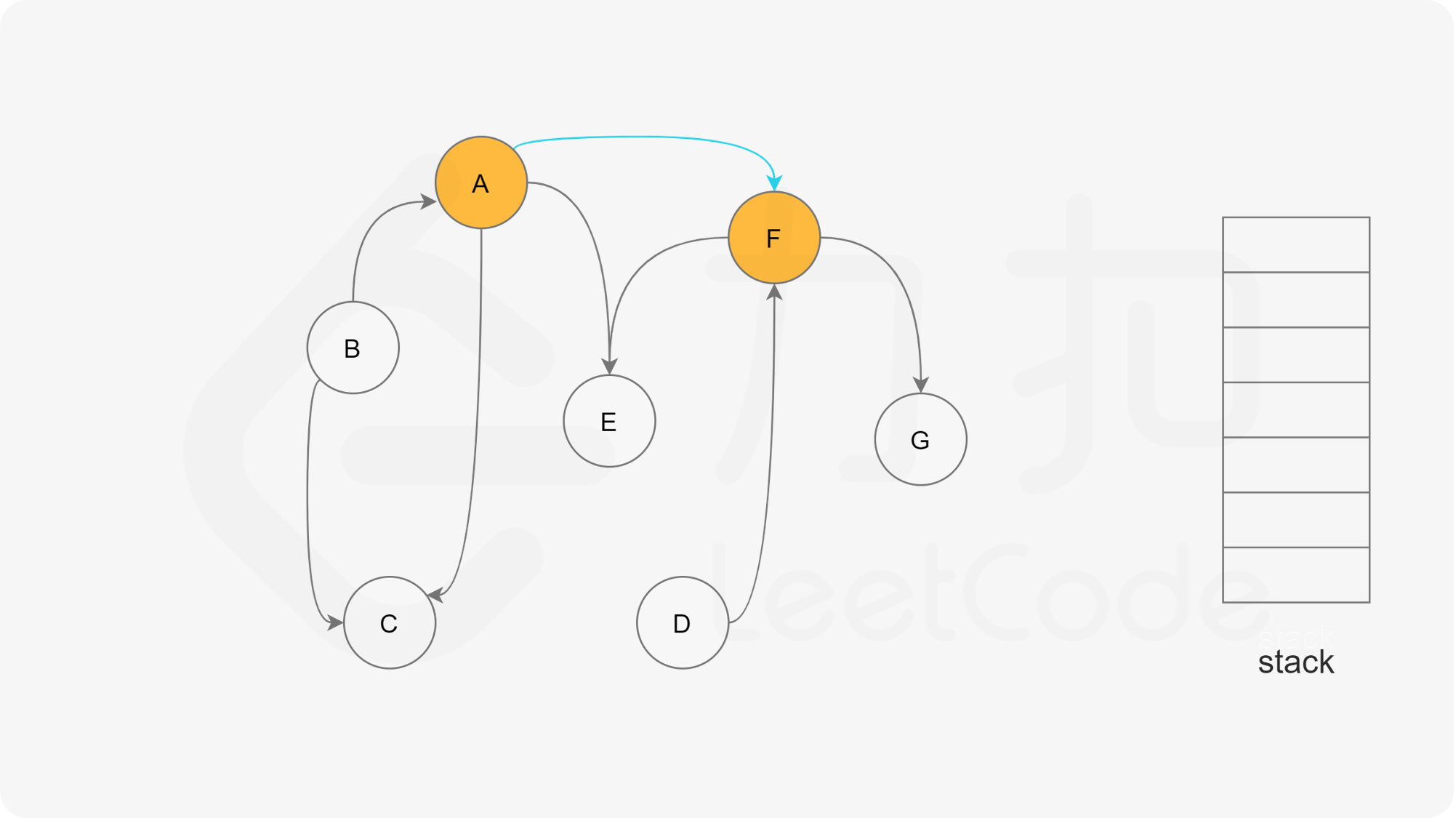
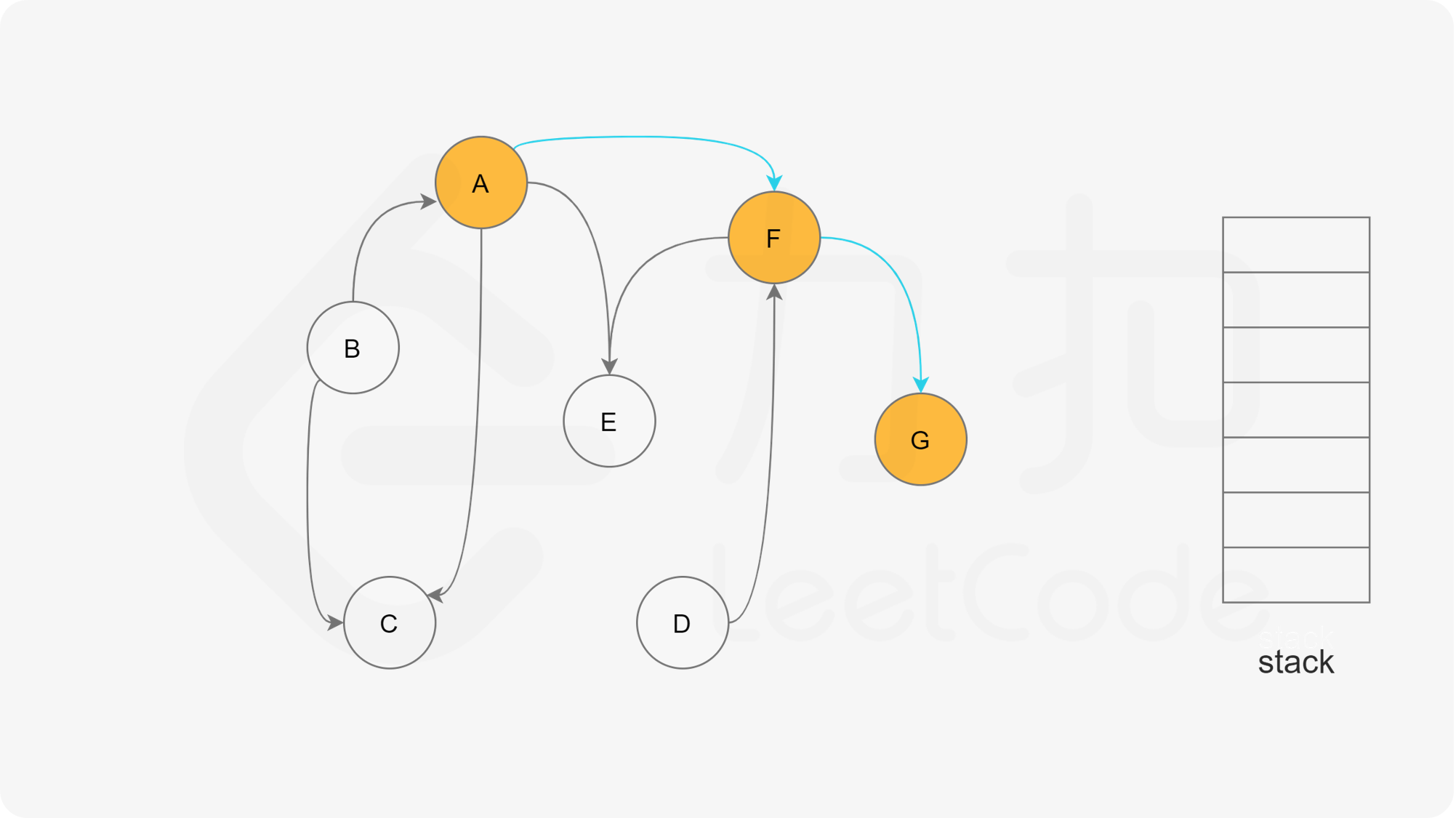
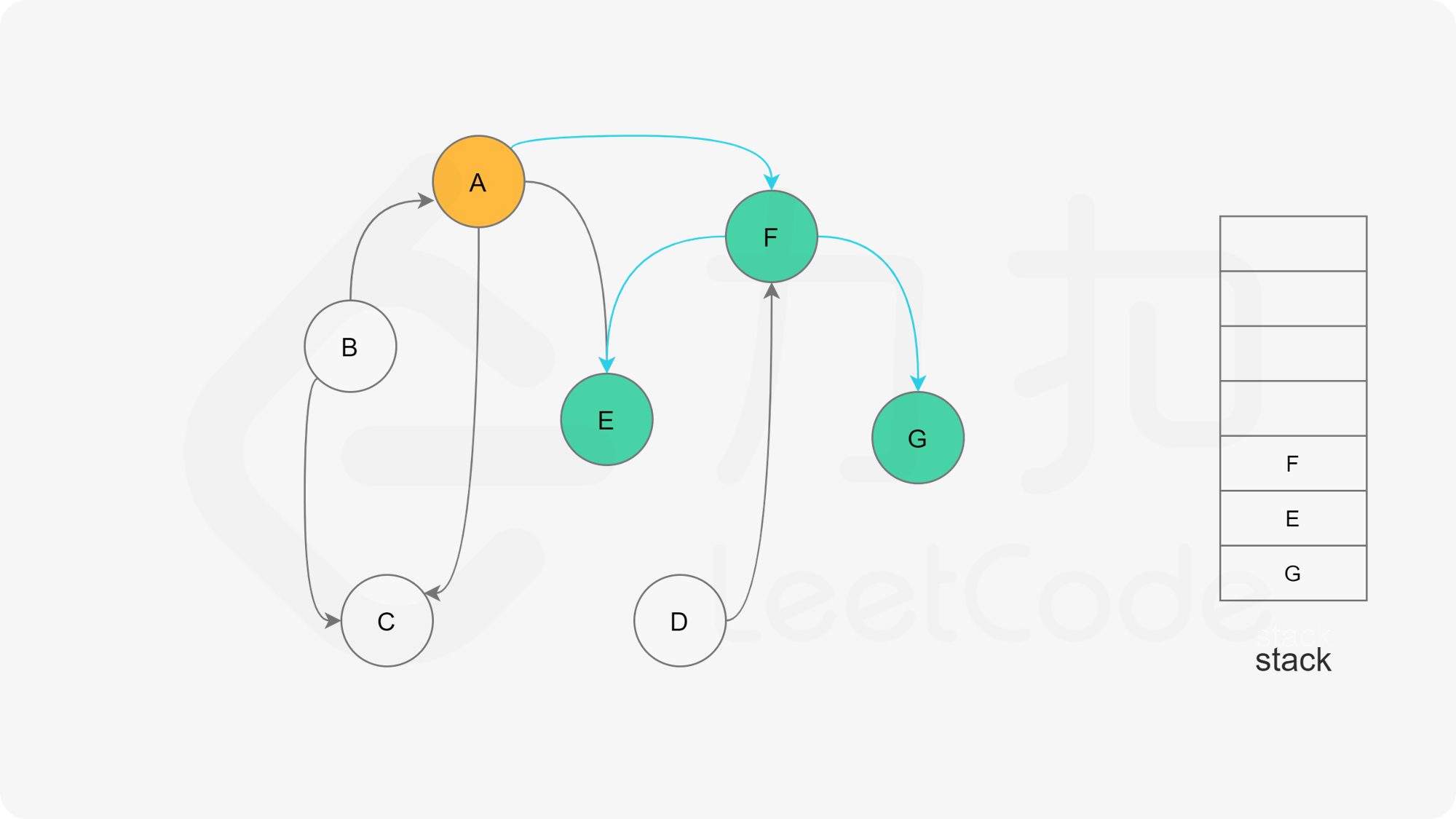
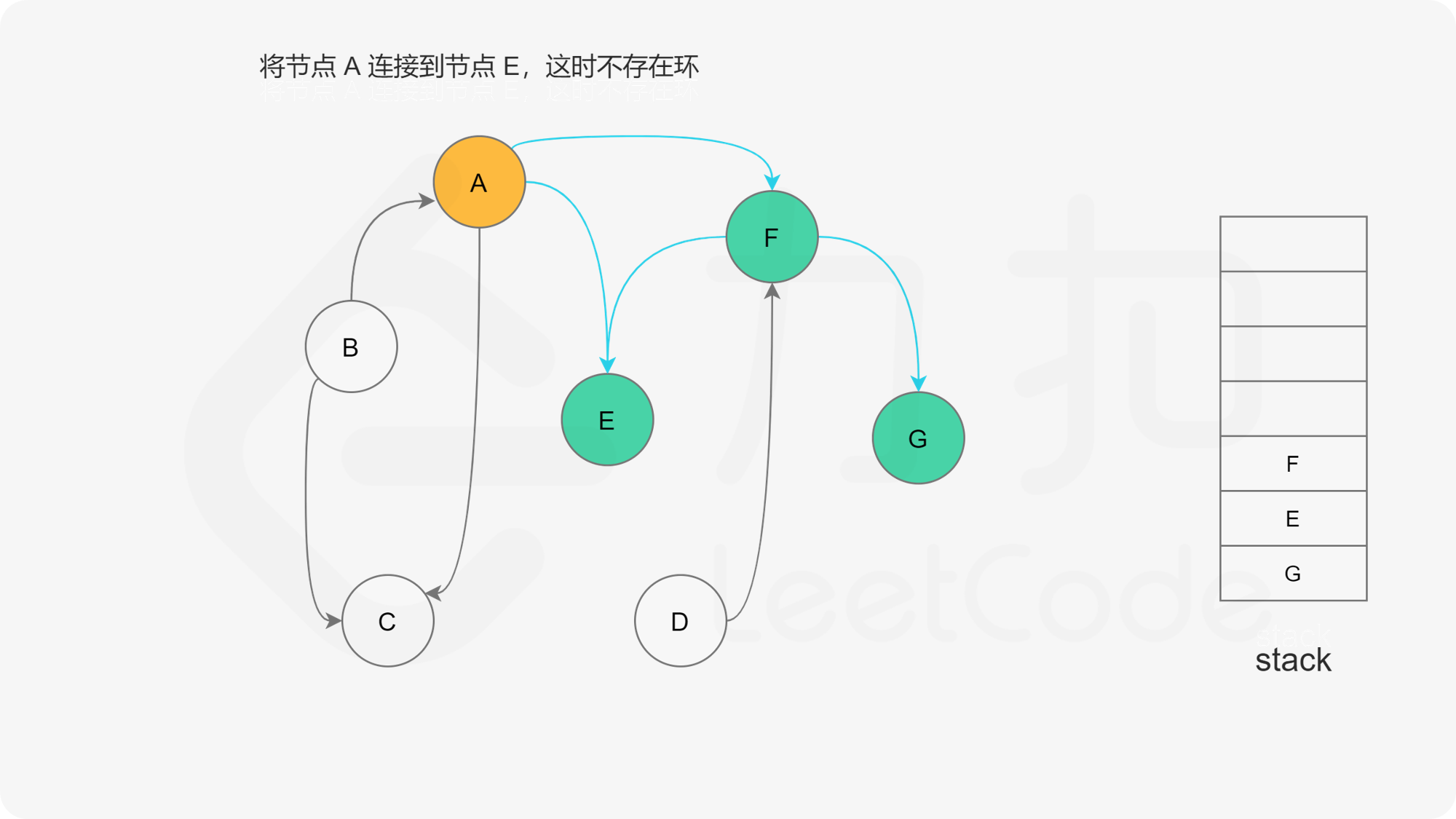
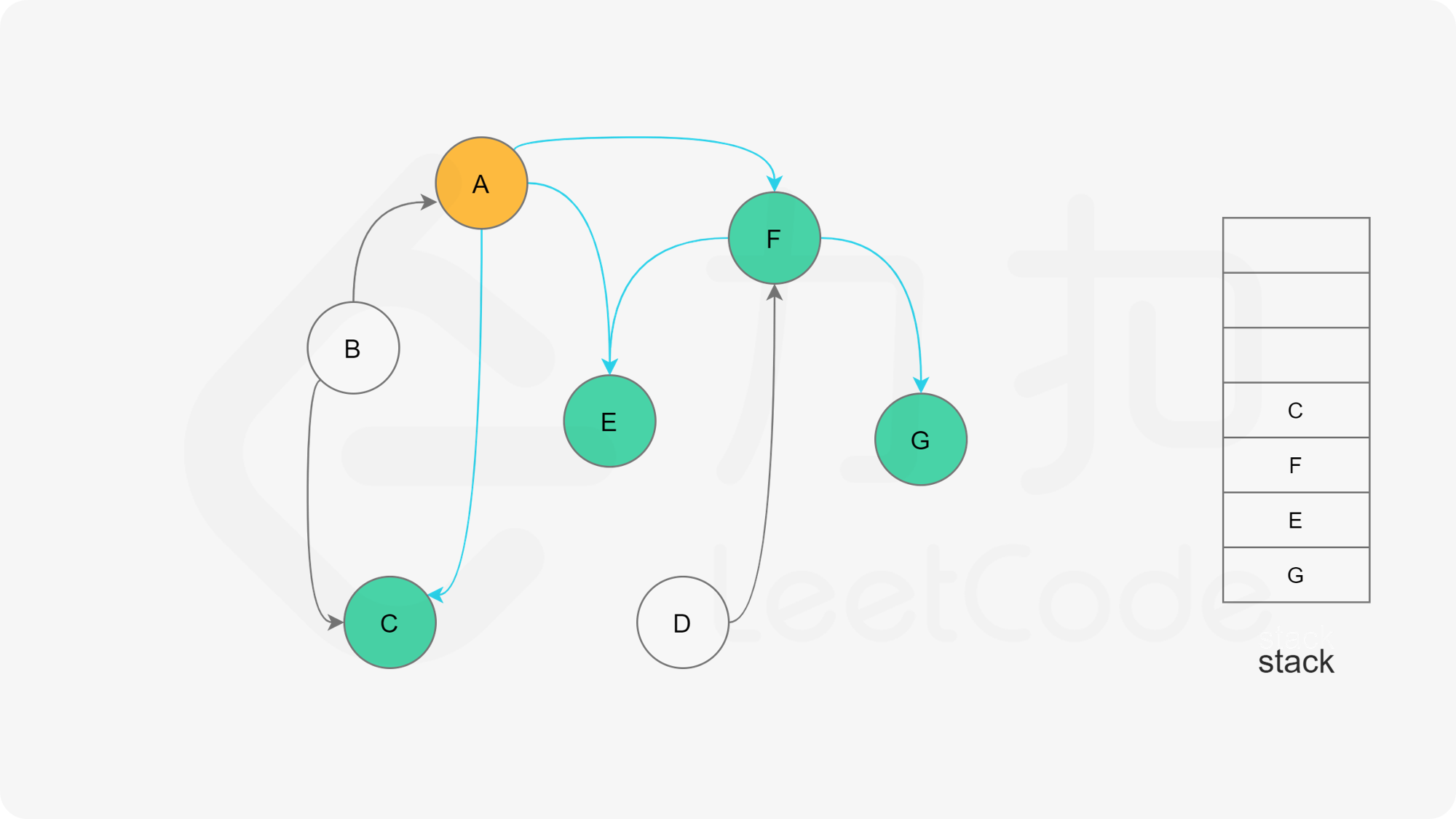
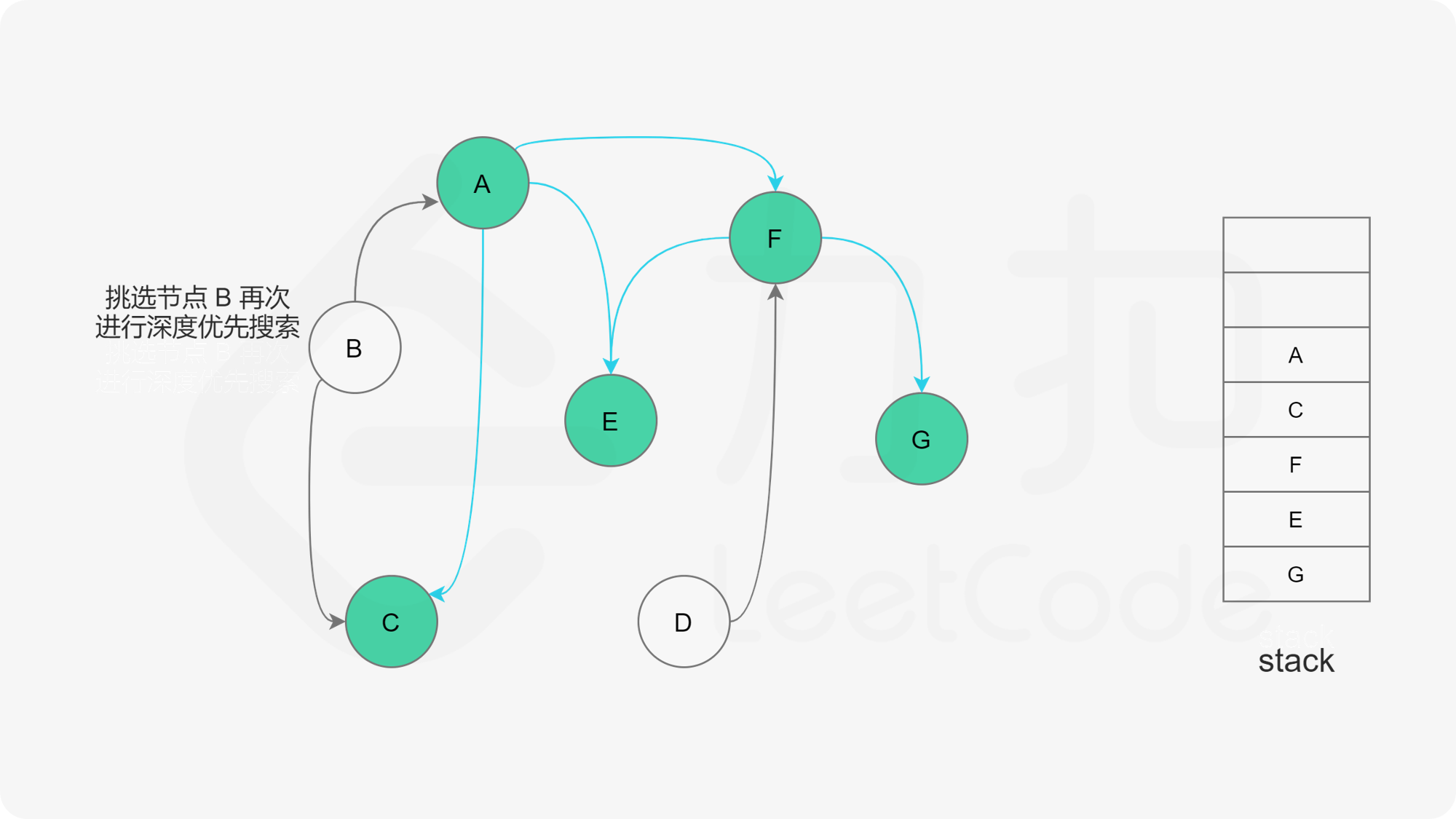
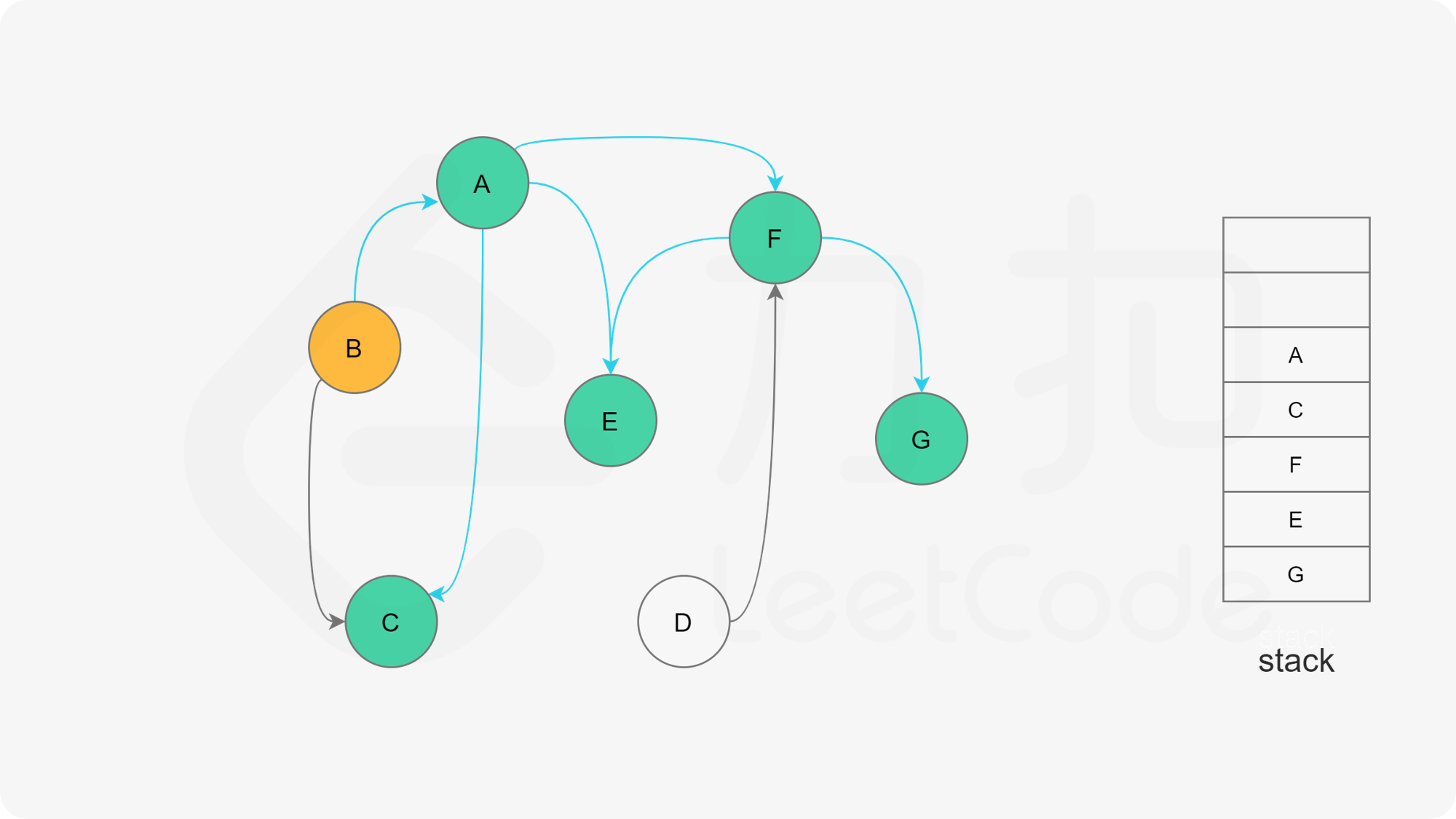
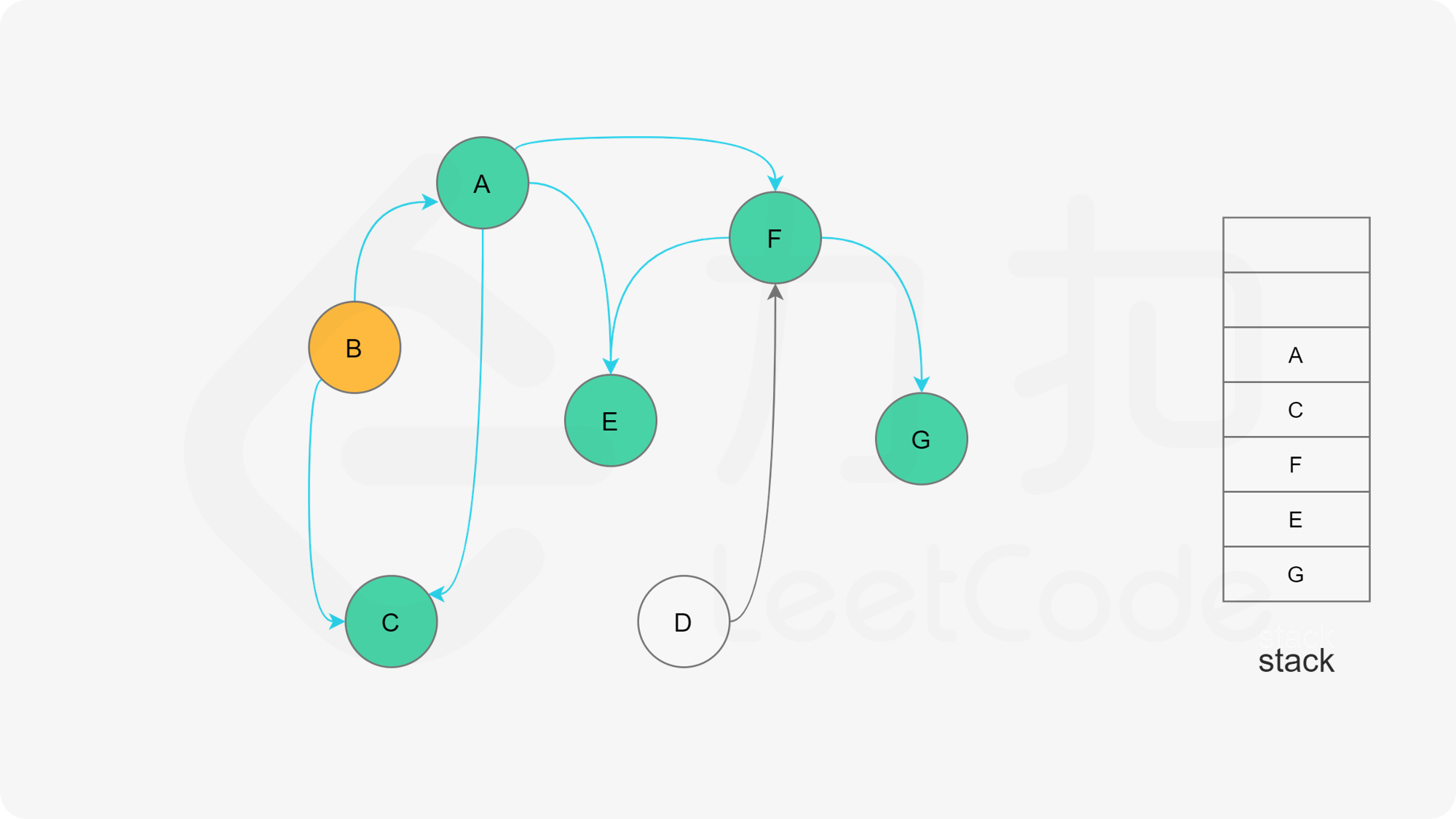
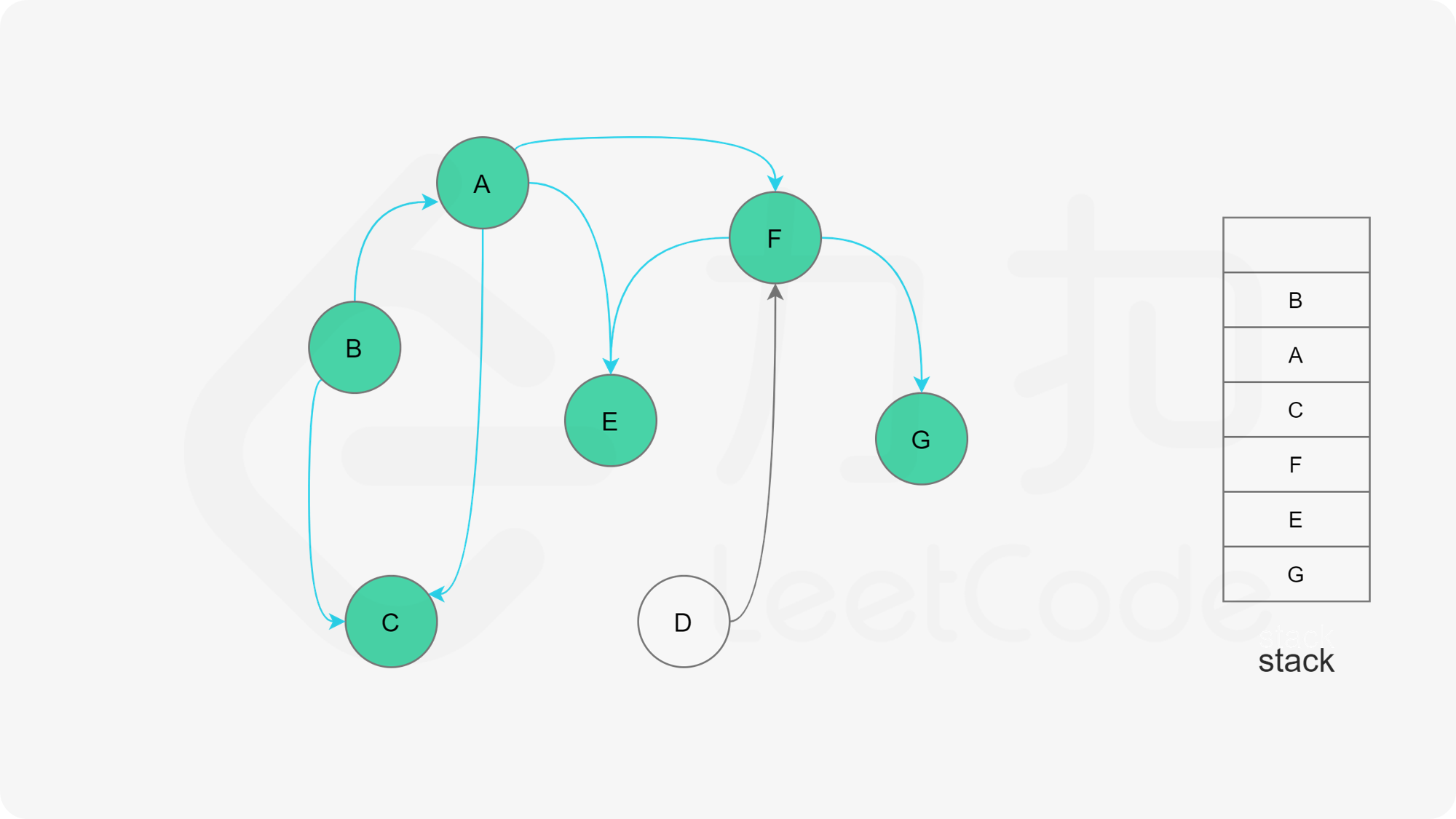
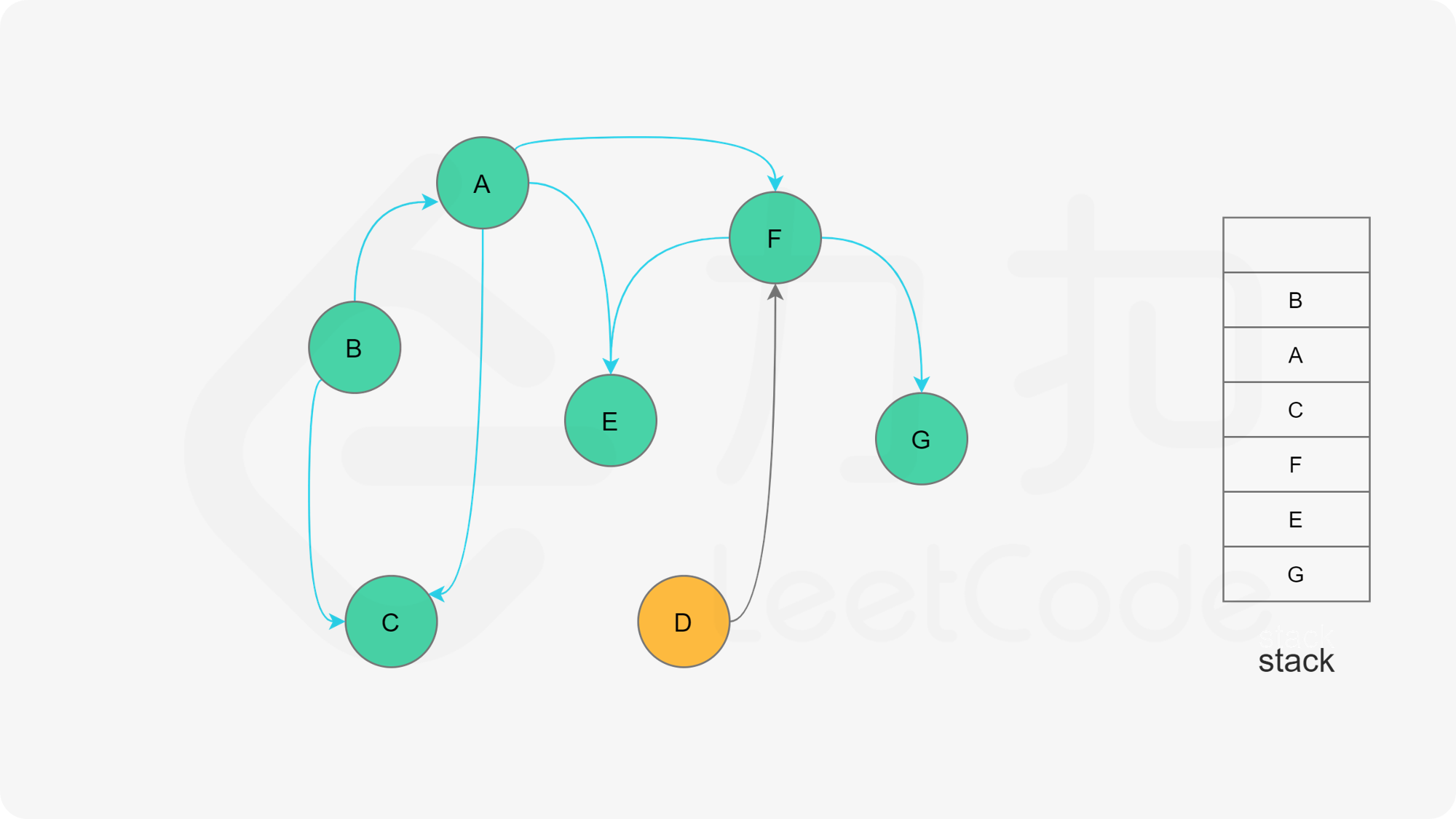
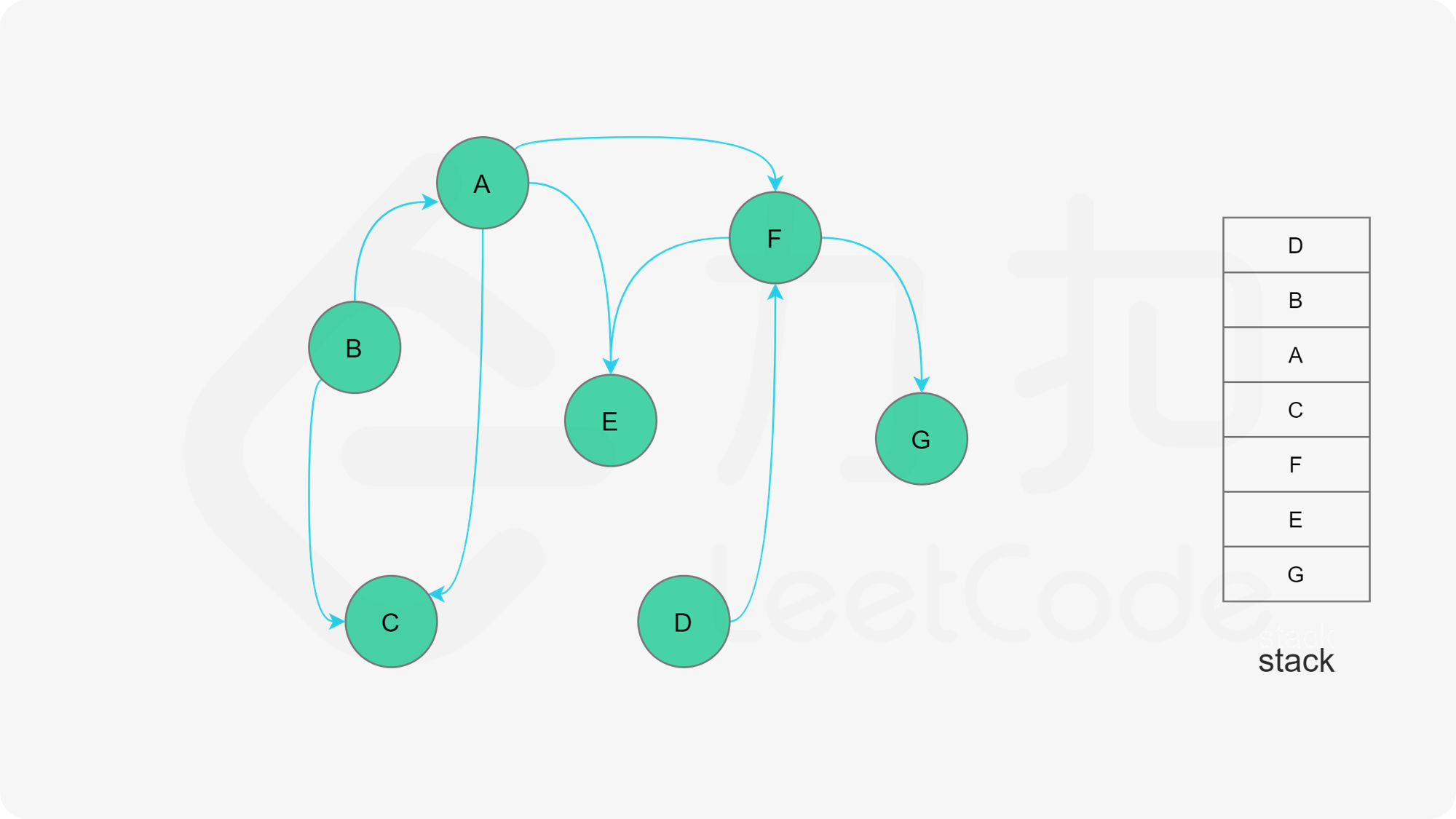
下面的幻灯片给出了深度优先搜索的可视化流程。图中的「白色」「黄色」「绿色」节点分别表示「未搜索」「搜索中」「已完成」的状态。

<DFS1,DFS2,DFS3,DFS4,DFS5,DFS6,DFS7,DFS8,DFS9,DFS10,DFS11,DFS12,DFS13,DFS14,DFS15,DFS16,DFS17,DFS18,DFS19,DFS20>

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
class Solution {
private:
    // 存储有向图
    vector<vector<int>> edges;
    // 标记每个节点的状态：0=未搜索，1=搜索中，2=已完成
    vector<int> visited;
    // 用数组来模拟栈，下标 0 为栈底，n-1 为栈顶
    vector<int> result;
    // 判断有向图中是否有环
    bool valid = true;

public:
    void dfs(int u) {
        // 将节点标记为「搜索中」
        visited[u] = 1;
        // 搜索其相邻节点
        // 只要发现有环，立刻停止搜索
        for (int v: edges[u]) {
            // 如果「未搜索」那么搜索相邻节点
            if (visited[v] == 0) {
                dfs(v);
                if (!valid) {
                    return;
                }
            }
            // 如果「搜索中」说明找到了环
            else if (visited[v] == 1) {
                valid = false;
                return;
            }
        }
        // 将节点标记为「已完成」
        visited[u] = 2;
        // 将节点入栈
        result.push_back(u);
    }

    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        edges.resize(numCourses);
        visited.resize(numCourses);
        for (const auto& info: prerequisites) {
            edges[info[1]].push_back(info[0]);
        }
        // 每次挑选一个「未搜索」的节点，开始进行深度优先搜索
        for (int i = 0; i < numCourses && valid; ++i) {
            if (!visited[i]) {
                dfs(i);
            }
        }
        if (!valid) {
            return {};
        }
        // 如果没有环，那么就有拓扑排序
        // 注意下标 0 为栈底，因此需要将数组反序输出
        reverse(result.begin(), result.end());
        return result;
    }
};
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
class Solution {
    // 存储有向图
    List<List<Integer>> edges;
    // 标记每个节点的状态：0=未搜索，1=搜索中，2=已完成
    int[] visited;
    // 用数组来模拟栈，下标 n-1 为栈底，0 为栈顶
    int[] result;
    // 判断有向图中是否有环
    boolean valid = true;
    // 栈下标
    int index;

    public int[] findOrder(int numCourses, int[][] prerequisites) {
        edges = new ArrayList<List<Integer>>();
        for (int i = 0; i < numCourses; ++i) {
            edges.add(new ArrayList<Integer>());
        }
        visited = new int[numCourses];
        result = new int[numCourses];
        index = numCourses - 1;
        for (int[] info : prerequisites) {
            edges.get(info[1]).add(info[0]);
        }
        // 每次挑选一个「未搜索」的节点，开始进行深度优先搜索
        for (int i = 0; i < numCourses && valid; ++i) {
            if (visited[i] == 0) {
                dfs(i);
            }
        }
        if (!valid) {
            return new int[0];
        }
        // 如果没有环，那么就有拓扑排序
        return result;
    }

    public void dfs(int u) {
        // 将节点标记为「搜索中」
        visited[u] = 1;
        // 搜索其相邻节点
        // 只要发现有环，立刻停止搜索
        for (int v: edges.get(u)) {
            // 如果「未搜索」那么搜索相邻节点
            if (visited[v] == 0) {
                dfs(v);
                if (!valid) {
                    return;
                }
            }
            // 如果「搜索中」说明找到了环
            else if (visited[v] == 1) {
                valid = false;
                return;
            }
        }
        // 将节点标记为「已完成」
        visited[u] = 2;
        // 将节点入栈
        result[index--] = u;
    }
}
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Solution:
    def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:
        # 存储有向图
        edges = collections.defaultdict(list)
        # 标记每个节点的状态：0=未搜索，1=搜索中，2=已完成
        visited = [0] * numCourses
        # 用数组来模拟栈，下标 0 为栈底，n-1 为栈顶
        result = list()
        # 判断有向图中是否有环
        valid = True

        for info in prerequisites:
            edges[info[1]].append(info[0])
        
        def dfs(u: int):
            nonlocal valid
            # 将节点标记为「搜索中」
            visited[u] = 1
            # 搜索其相邻节点
            # 只要发现有环，立刻停止搜索
            for v in edges[u]:
                # 如果「未搜索」那么搜索相邻节点
                if visited[v] == 0:
                    dfs(v)
                    if not valid:
                        return
                # 如果「搜索中」说明找到了环
                elif visited[v] == 1:
                    valid = False
                    return
            # 将节点标记为「已完成」
            visited[u] = 2
            # 将节点入栈
            result.append(u)
        
        # 每次挑选一个「未搜索」的节点，开始进行深度优先搜索
        for i in range(numCourses):
            if valid and not visited[i]:
                dfs(i)
        
        if not valid:
            return list()
        
        # 如果没有环，那么就有拓扑排序
        # 注意下标 0 为栈底，因此需要将数组反序输出
        return result[::-1]
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
func findOrder(numCourses int, prerequisites [][]int) []int {
    var (
        edges = make([][]int, numCourses)
        visited = make([]int, numCourses)
        result []int
        valid bool = true
        dfs func(u int)
    )

    dfs = func(u int) {
        visited[u] = 1
        for _, v := range edges[u] {
            if visited[v] == 0 {
                dfs(v)
                if !valid {
                    return
                }
            } else if visited[v] == 1 {
                valid = false
                return
            }
        }
        visited[u] = 2
        result = append(result, u)
    }

    for _, info := range prerequisites {
        edges[info[1]] = append(edges[info[1]], info[0])
    }

    for i := 0; i < numCourses && valid; i++ {
        if visited[i] == 0 {
            dfs(i)
        }
    }
    if !valid {
        return []int{}
    }
    for i := 0; i < len(result)/2; i ++ {
        result[i], result[numCourses-i-1] = result[numCourses-i-1], result[i]
    }
    return result
}
[sol1-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
int** edges;
int* edgeColSize;
int* visited;
int* result;
int resultSize;
bool valid;

void dfs(int u) {
    visited[u] = 1;
    for (int i = 0; i < edgeColSize[u]; ++i) {
        if (visited[edges[u][i]] == 0) {
            dfs(edges[u][i]);
            if (!valid) {
                return;
            }
        } else if (visited[edges[u][i]] == 1) {
            valid = false;
            return;
        }
    }
    visited[u] = 2;
    result[resultSize++] = u;
}

int* findOrder(int numCourses, int** prerequisites, int prerequisitesSize, int* prerequisitesColSize, int* returnSize) {
    valid = true;
    edges = (int**)malloc(sizeof(int*) * numCourses);
    for (int i = 0; i < numCourses; i++) {
        edges[i] = (int*)malloc(0);
    }
    edgeColSize = (int*)malloc(sizeof(int) * numCourses);
    memset(edgeColSize, 0, sizeof(int) * numCourses);
    visited = (int*)malloc(sizeof(int) * numCourses);
    memset(visited, 0, sizeof(int) * numCourses);
    for (int i = 0; i < prerequisitesSize; ++i) {
        int a = prerequisites[i][1], b = prerequisites[i][0];
        edgeColSize[a]++;
        edges[a] = (int*)realloc(edges[a], sizeof(int) * edgeColSize[a]);
        edges[a][edgeColSize[a] - 1] = b;
    }
    result = (int*)malloc(sizeof(int) * numCourses);
    resultSize = 0;
    for (int i = 0; i < numCourses && valid; ++i) {
        if (!visited[i]) {
            dfs(i);
        }
    }
    for (int i = 0; i < numCourses; i++) {
        free(edges[i]);
    }
    free(edges);
    free(edgeColSize);
    free(visited);
    if (!valid) {
        *returnSize = 0;
    } else
        *returnSize = numCourses;
    for (int i = 0; i < numCourses / 2; i++) {
        int t = result[i];
        result[i] = result[numCourses - i - 1], result[numCourses - i - 1] = t;
    }
    return result;
}

复杂度分析

  • 时间复杂度: $O(n+m)$，其中 $n$ 为课程数，$m$ 为先修课程的要求数。这其实就是对图进行深度优先搜索的时间复杂度。

  • 空间复杂度: $O(n+m)$。题目中是以列表形式给出的先修课程关系，为了对图进行深度优先搜索，我们需要存储成邻接表的形式，空间复杂度为 $O(n+m)$。在深度优先搜索的过程中，我们需要最多 $O(n)$ 的栈空间（递归）进行深度优先搜索，并且还需要若干个 $O(n)$ 的空间存储节点状态、最终答案等。

方法二：广度优先搜索

思路

方法一的深度优先搜索是一种「逆向思维」：最先被放入栈中的节点是在拓扑排序中最后面的节点。我们也可以使用正向思维，顺序地生成拓扑排序，这种方法也更加直观。

我们考虑拓扑排序中最前面的节点，该节点一定不会有任何入边，也就是它没有任何的先修课程要求。当我们将一个节点加入答案中后，我们就可以移除它的所有出边，代表着它的相邻节点少了一门先修课程的要求。如果某个相邻节点变成了「没有任何入边的节点」，那么就代表着这门课可以开始学习了。按照这样的流程，我们不断地将没有入边的节点加入答案，直到答案中包含所有的节点（得到了一种拓扑排序）或者不存在没有入边的节点（图中包含环）。

上面的想法类似于广度优先搜索，因此我们可以将广度优先搜索的流程与拓扑排序的求解联系起来。

算法

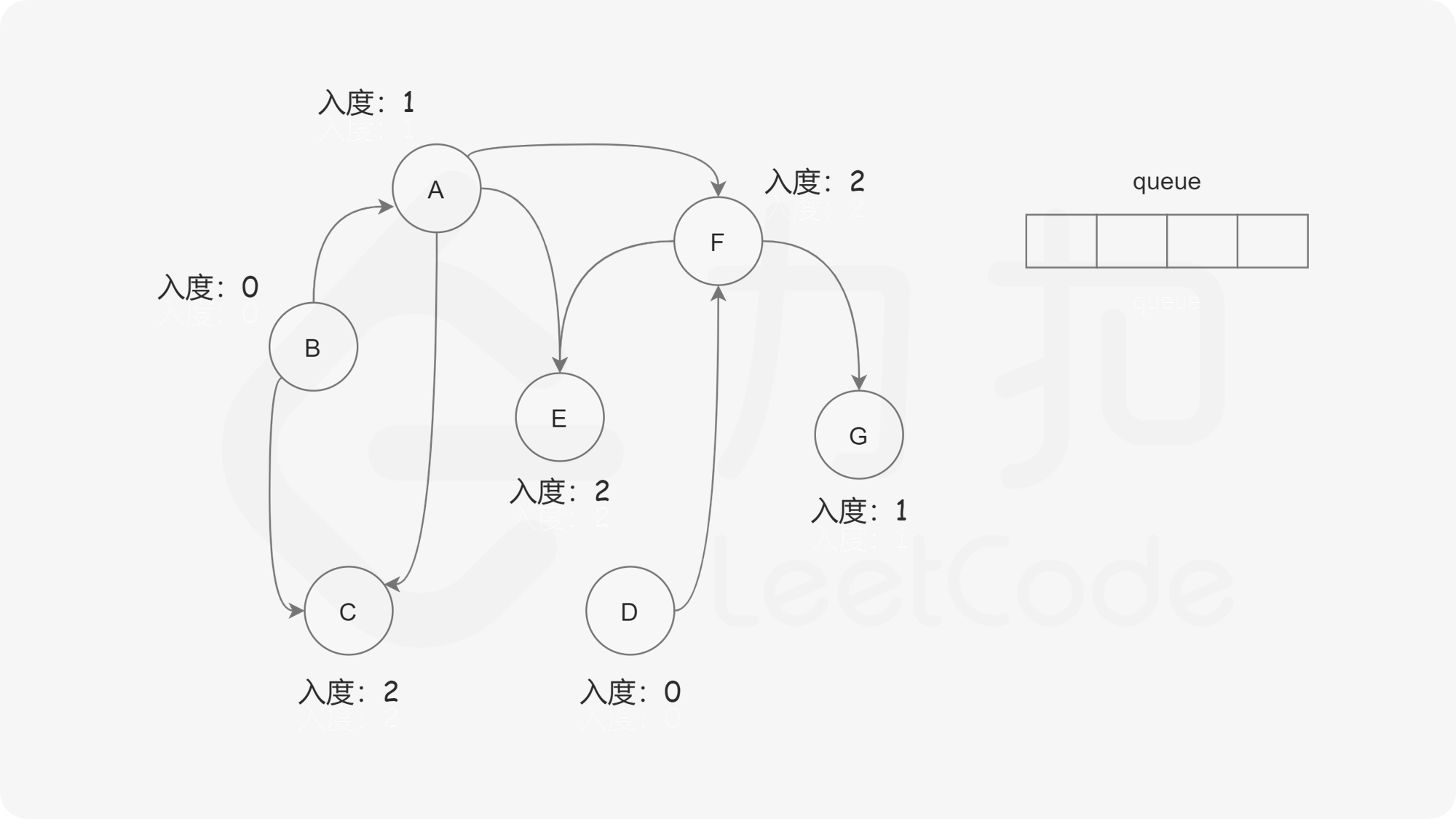
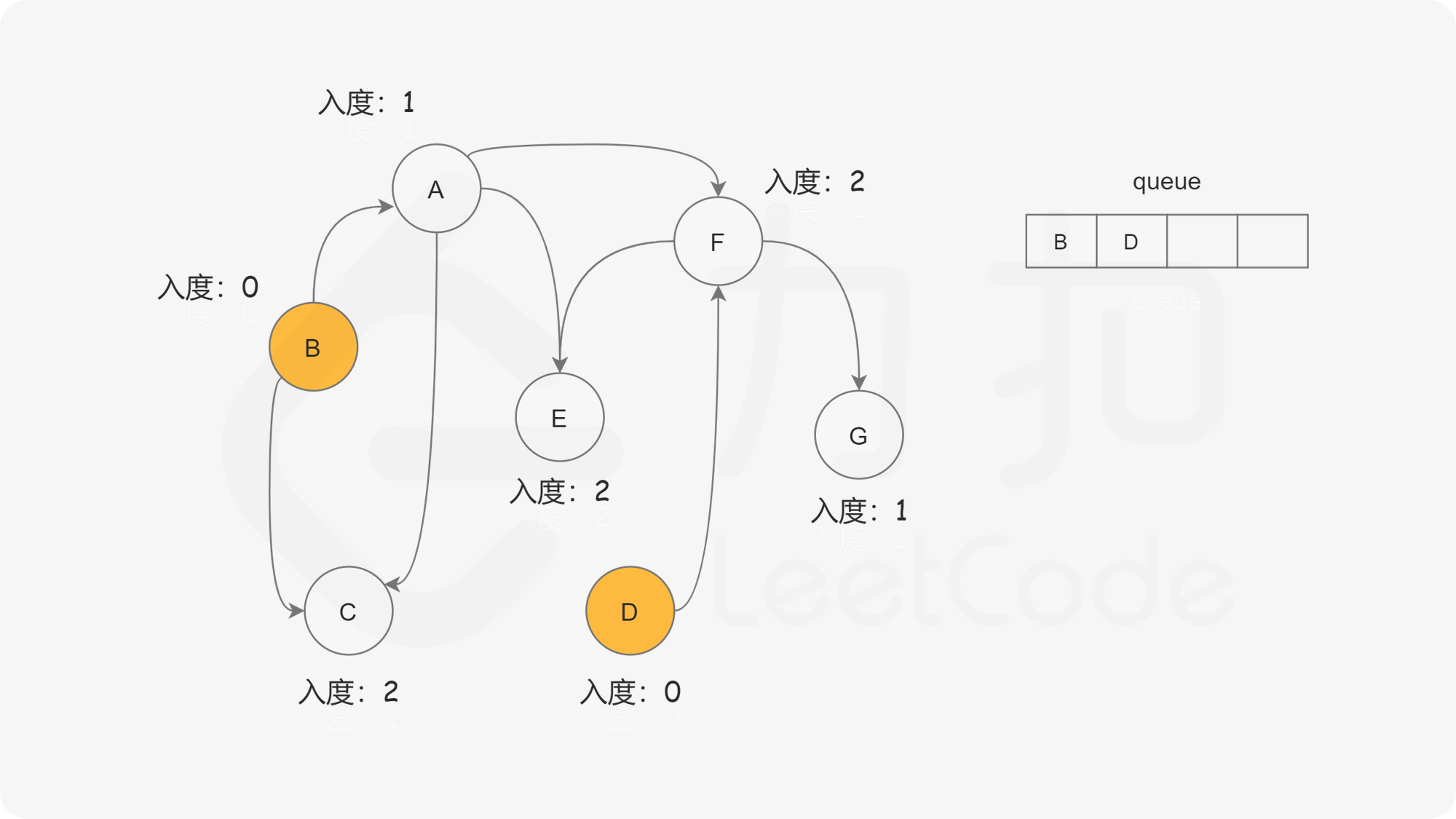
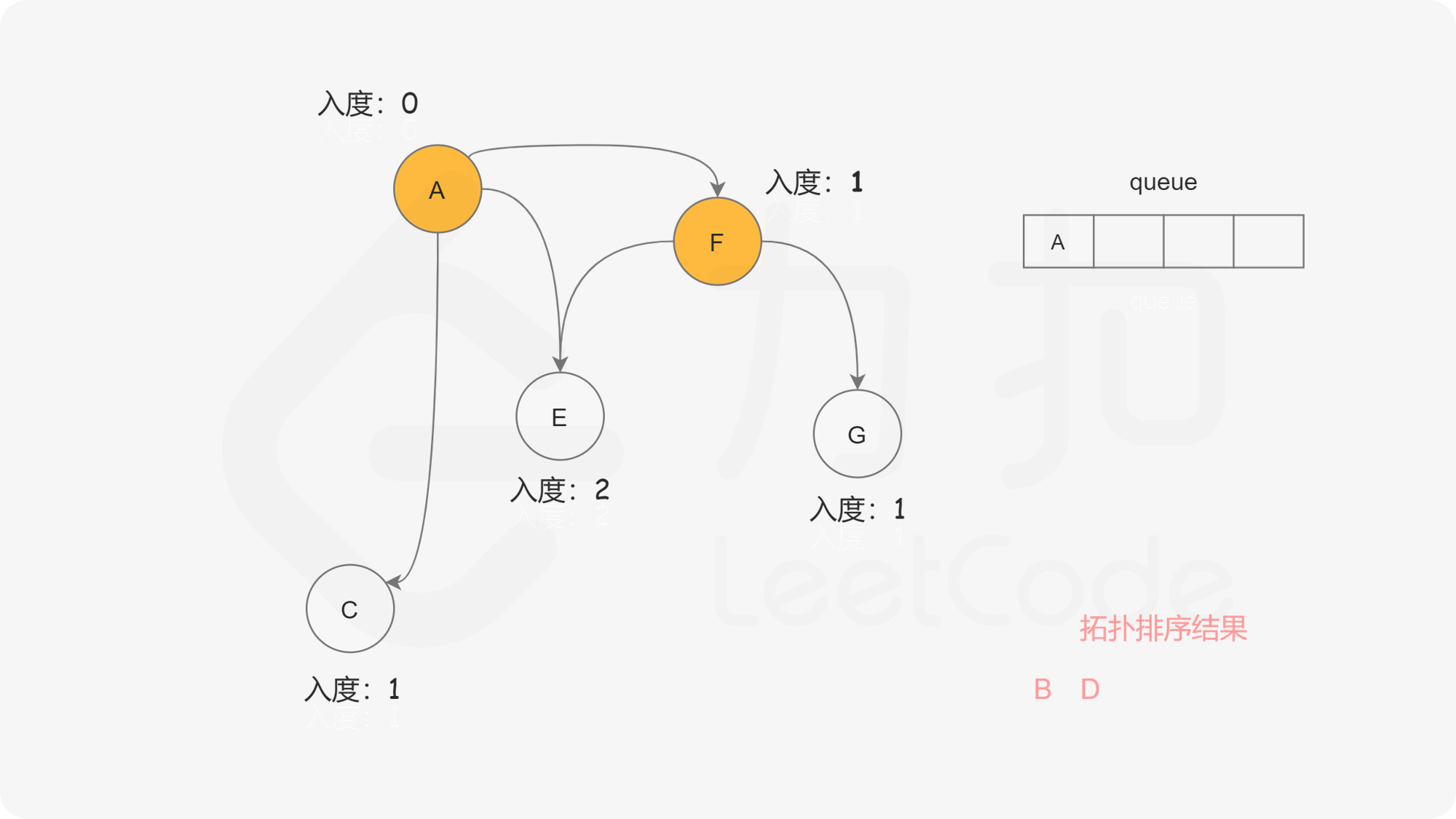
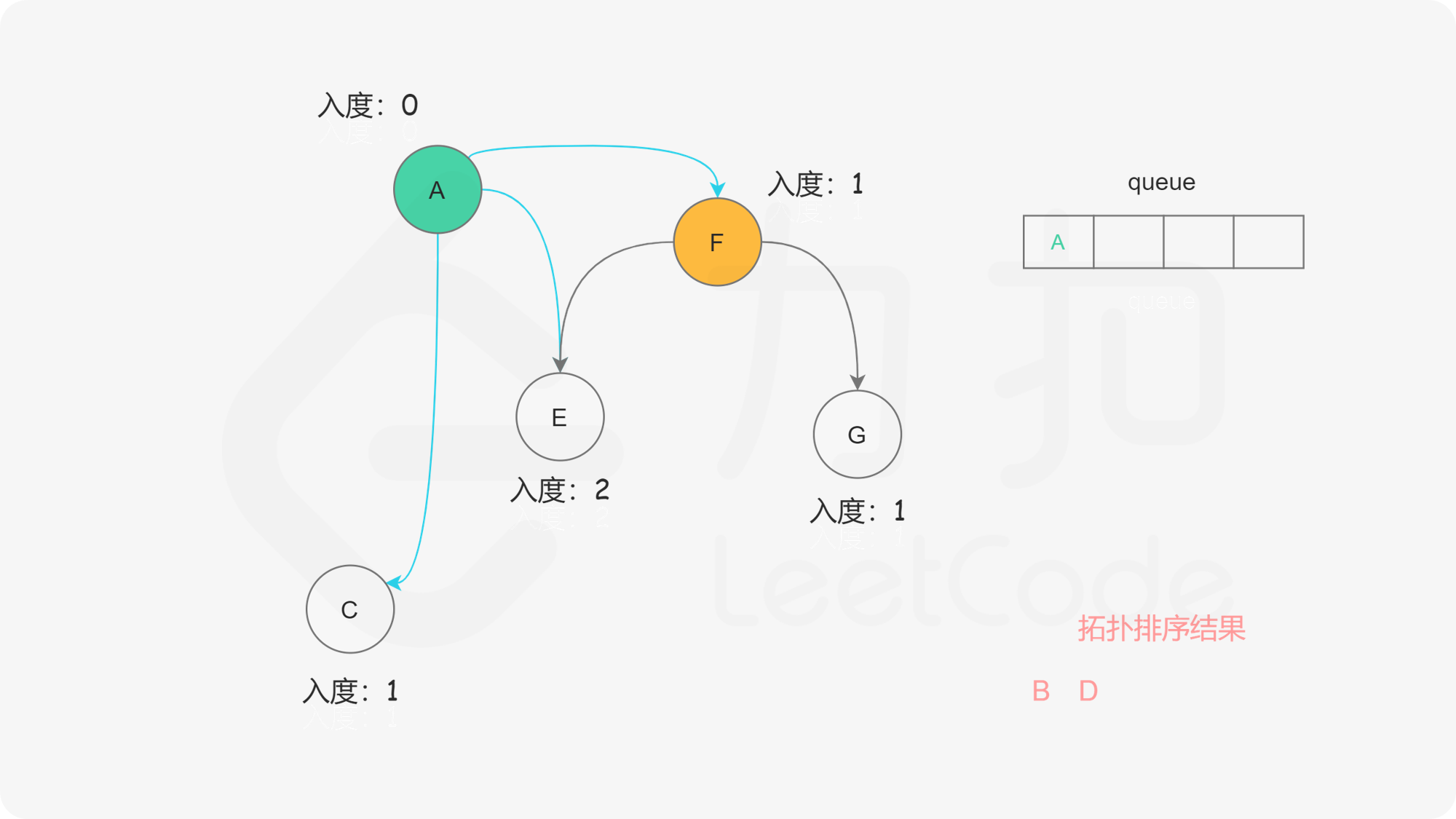
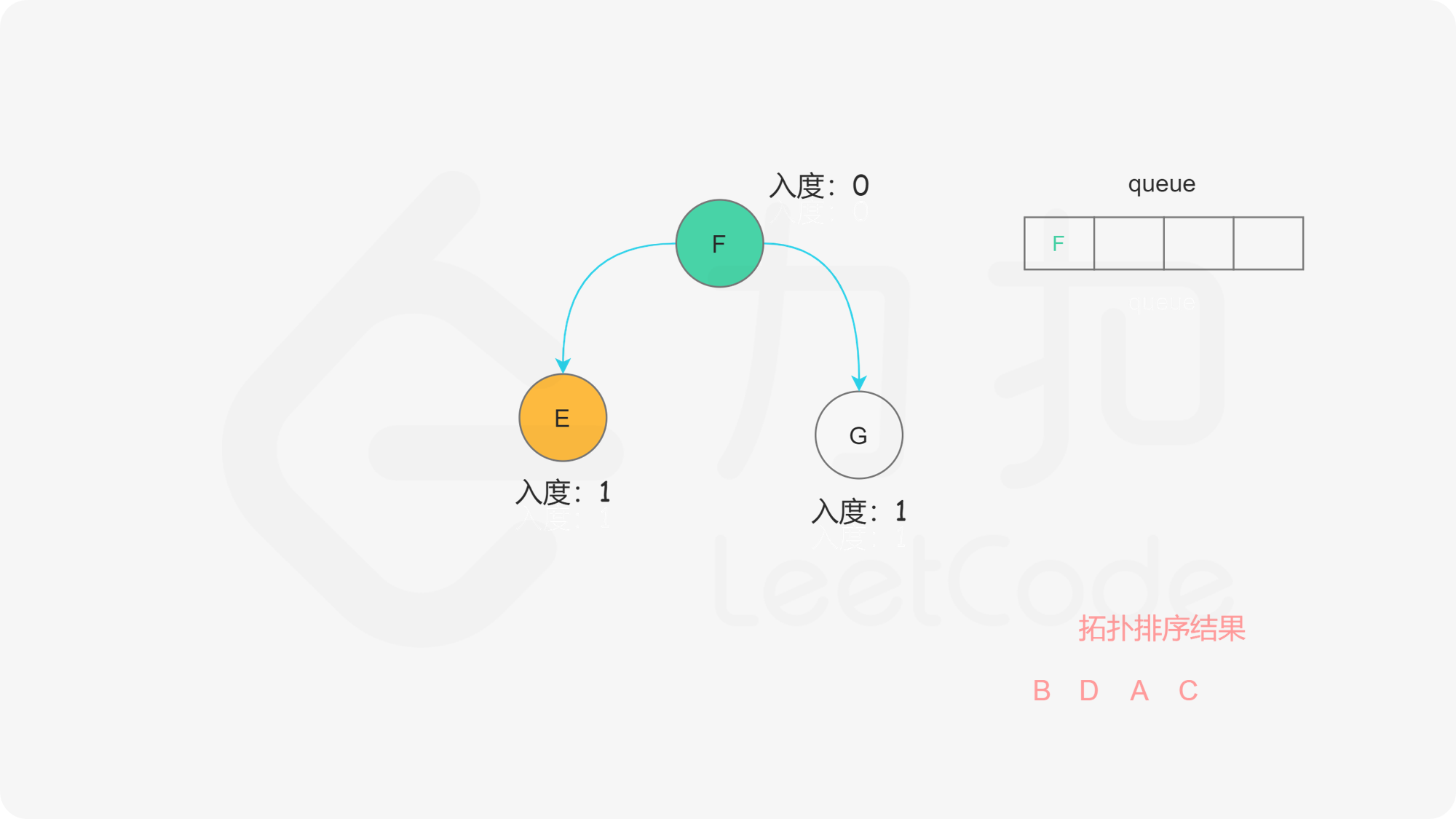
我们使用一个队列来进行广度优先搜索。开始时，所有入度为 $0$ 的节点都被放入队列中，它们就是可以作为拓扑排序最前面的节点，并且它们之间的相对顺序是无关紧要的。

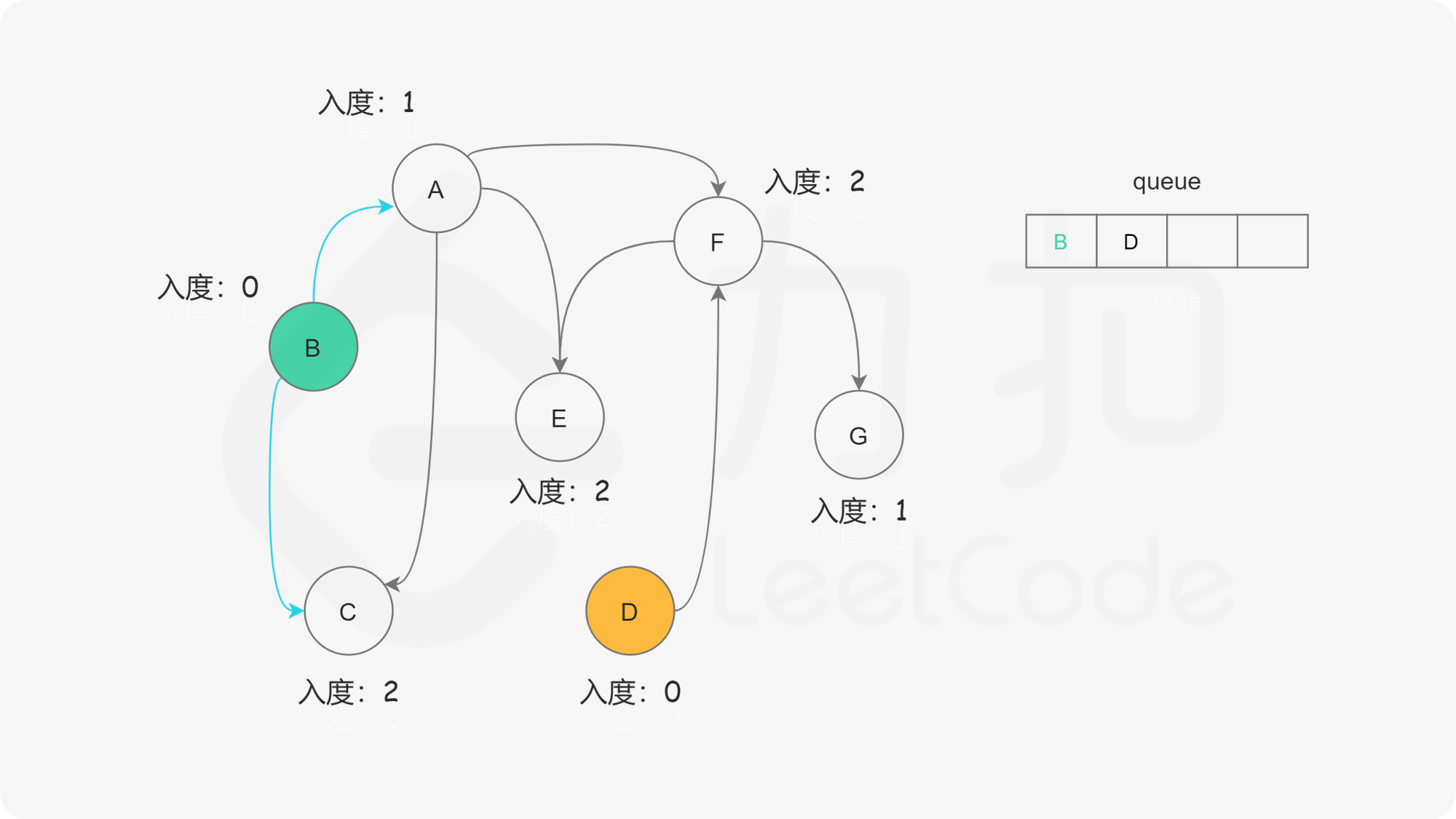
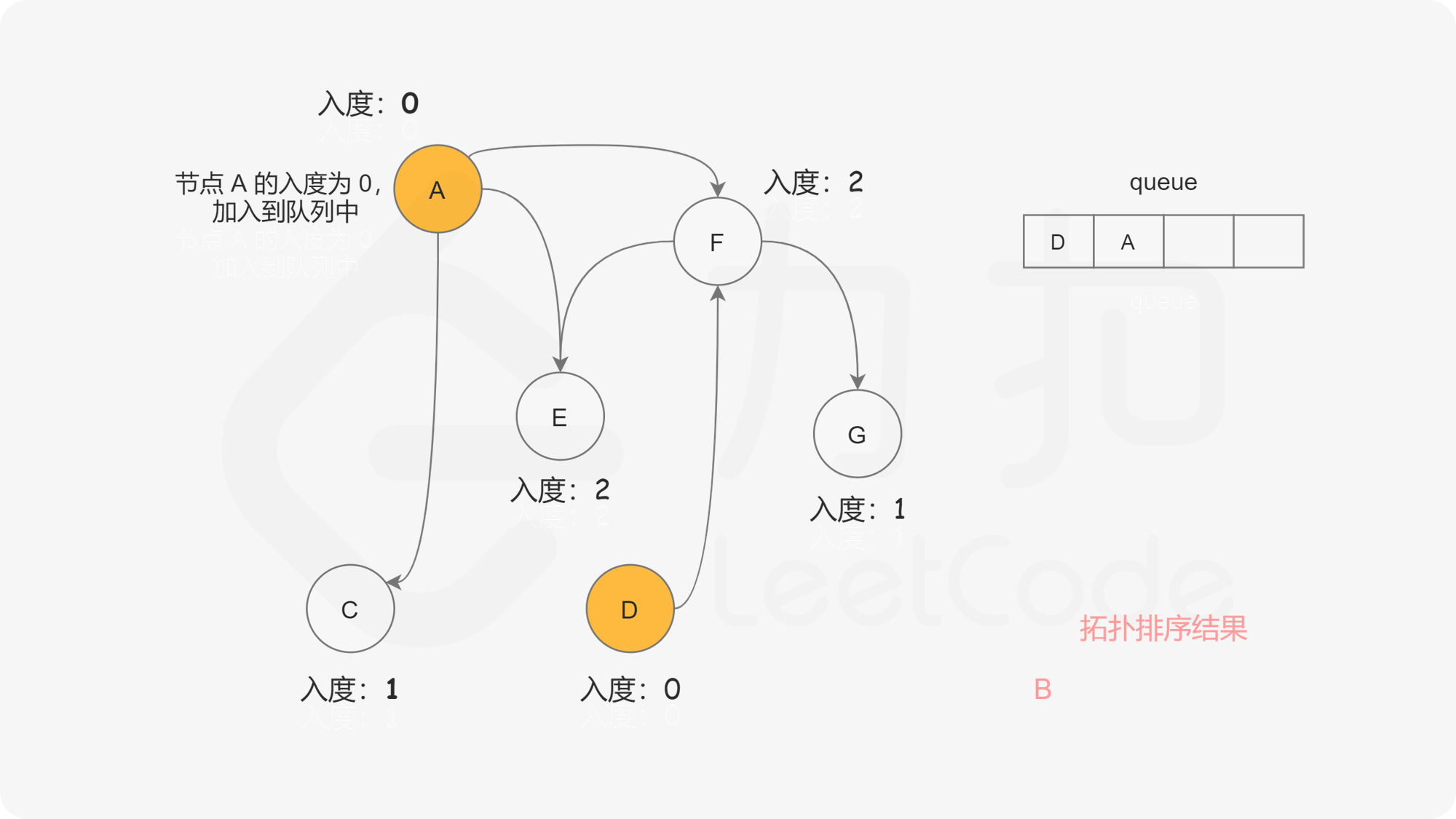
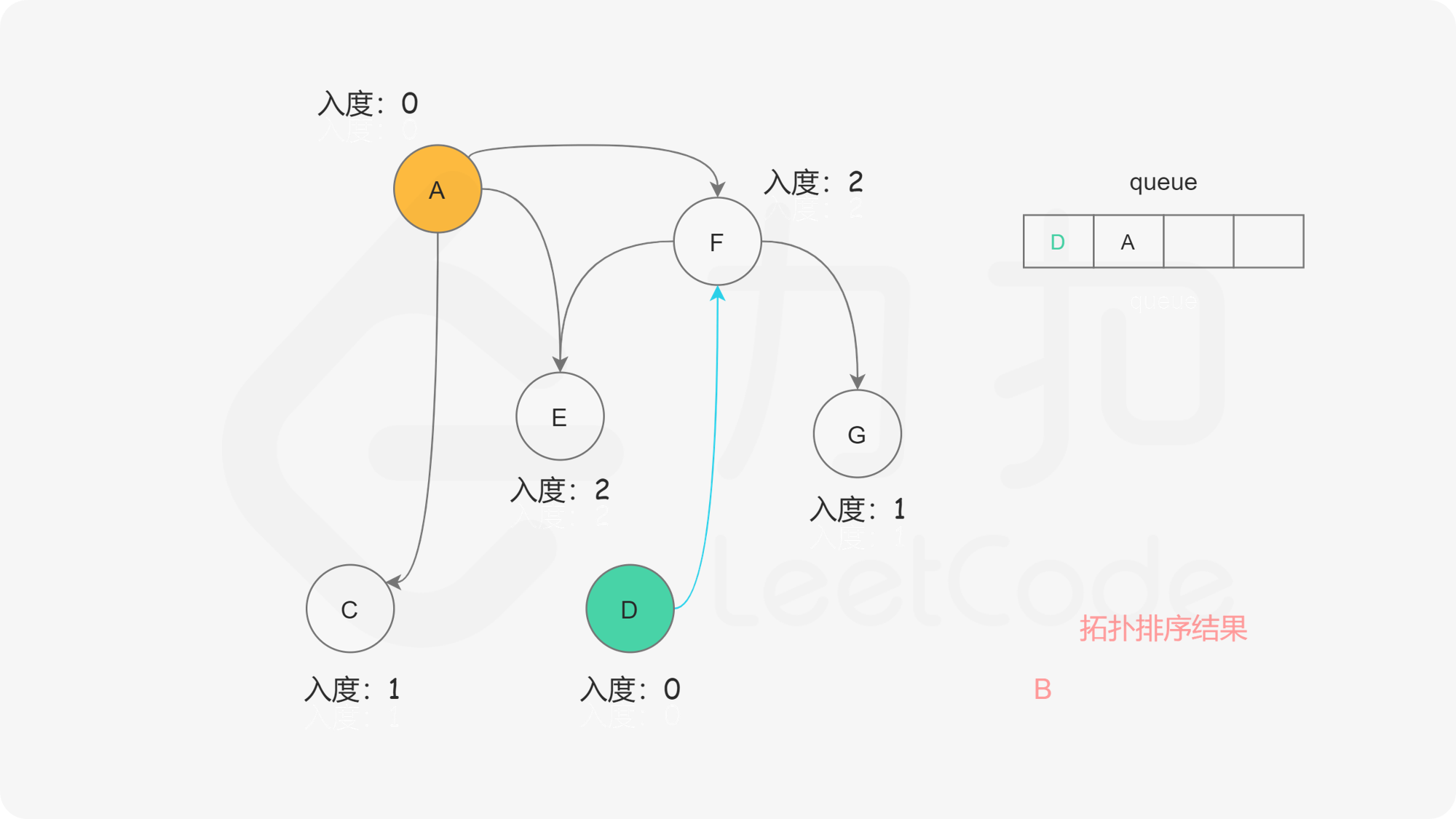
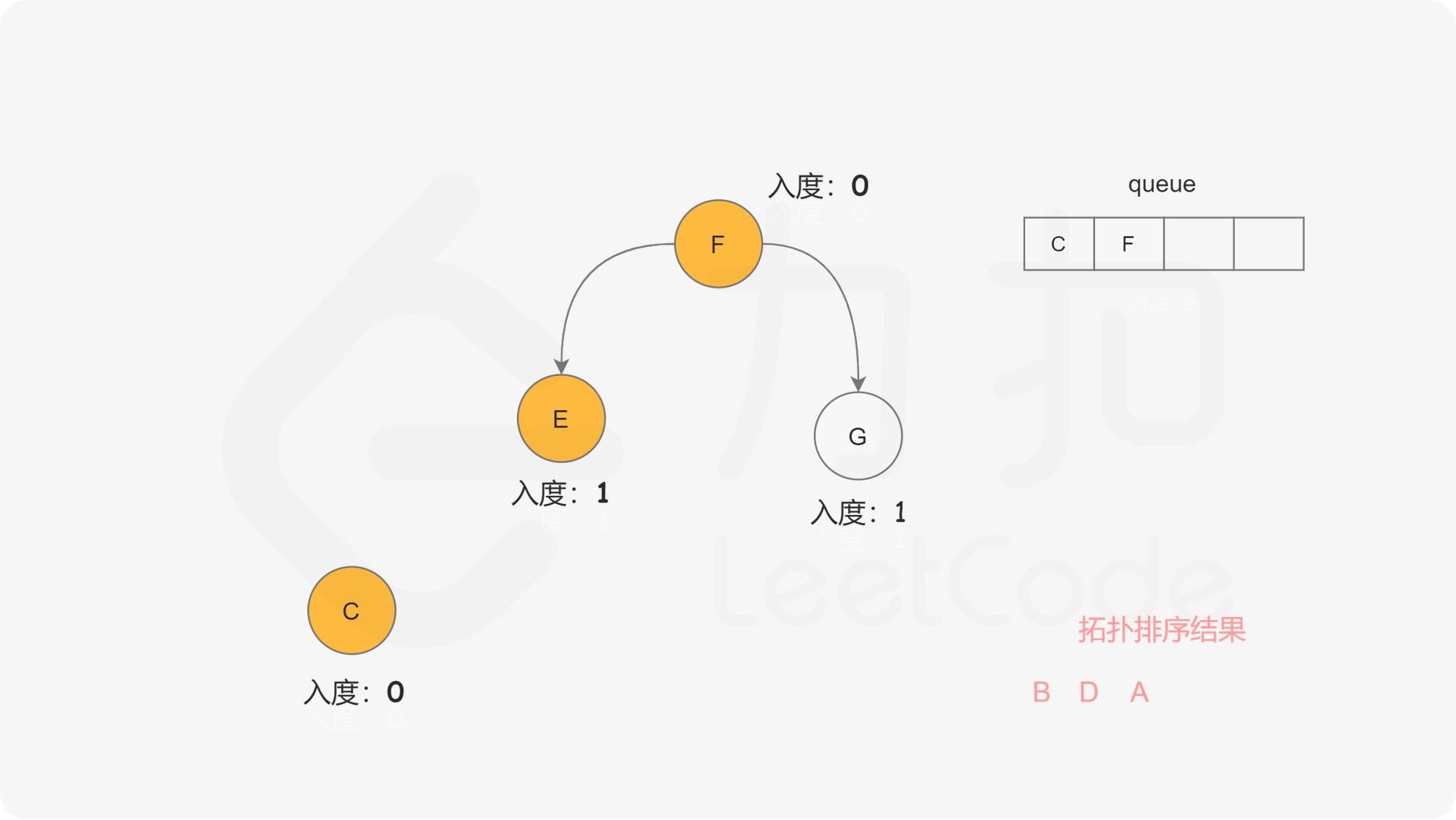
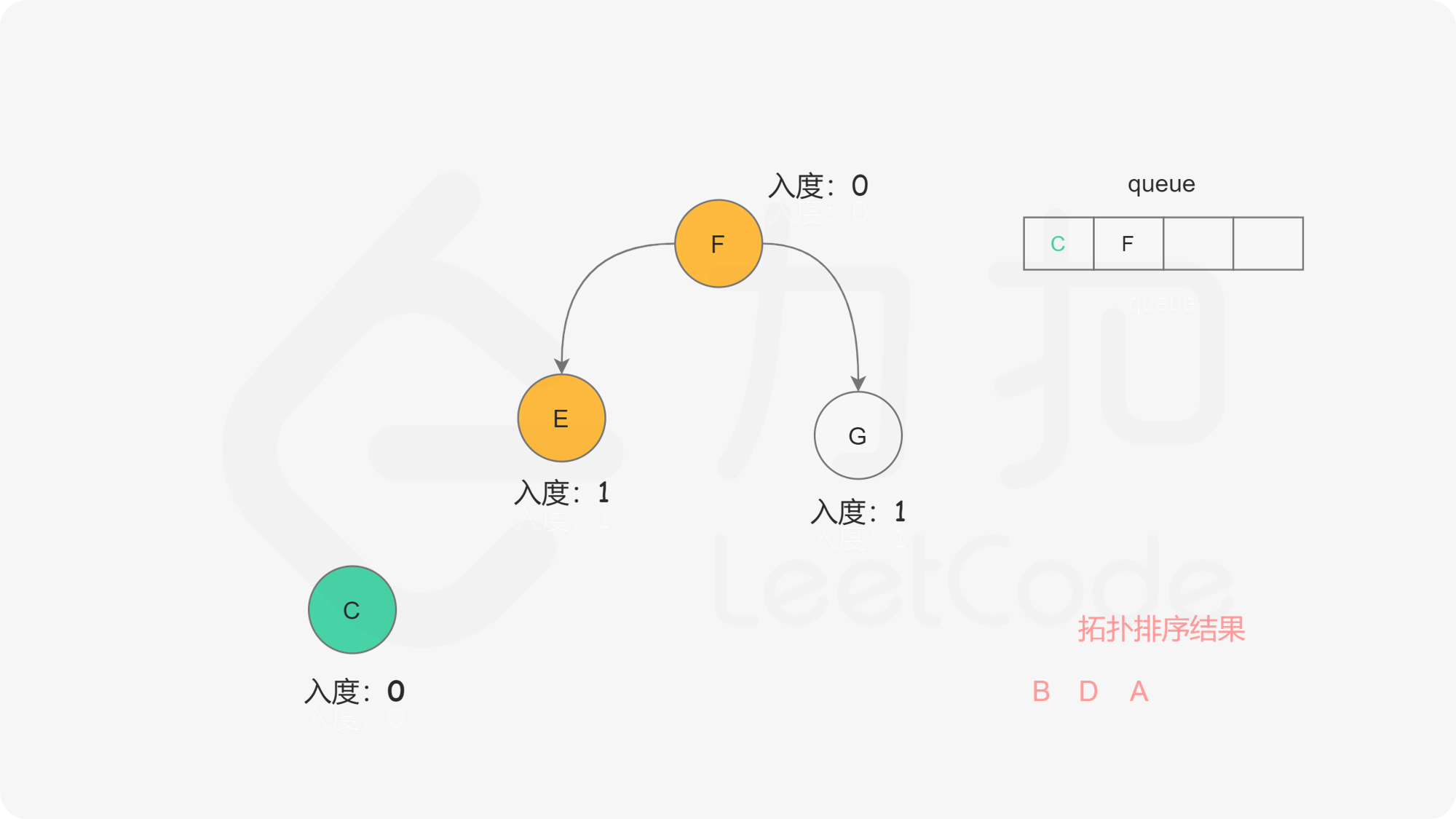
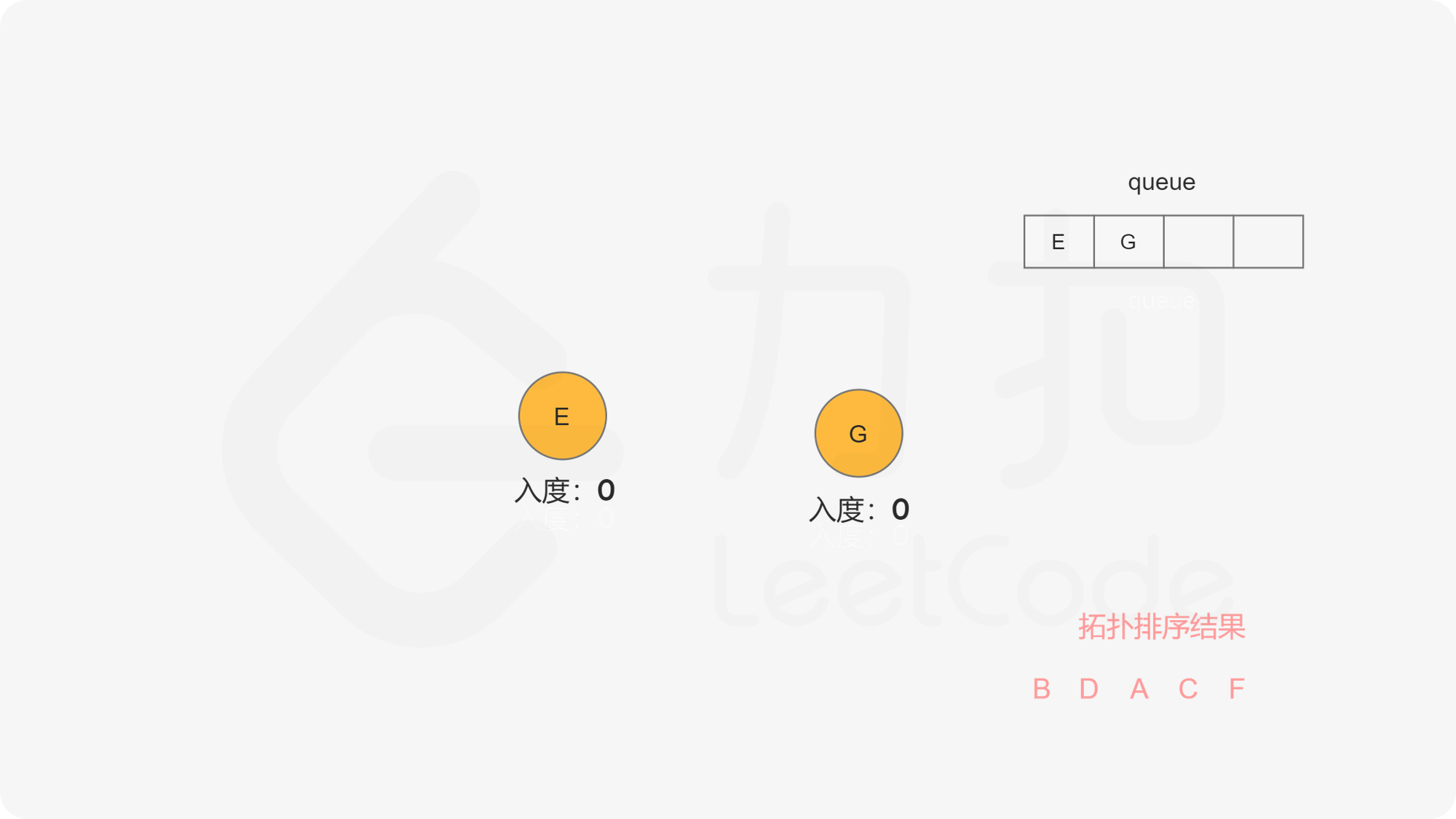
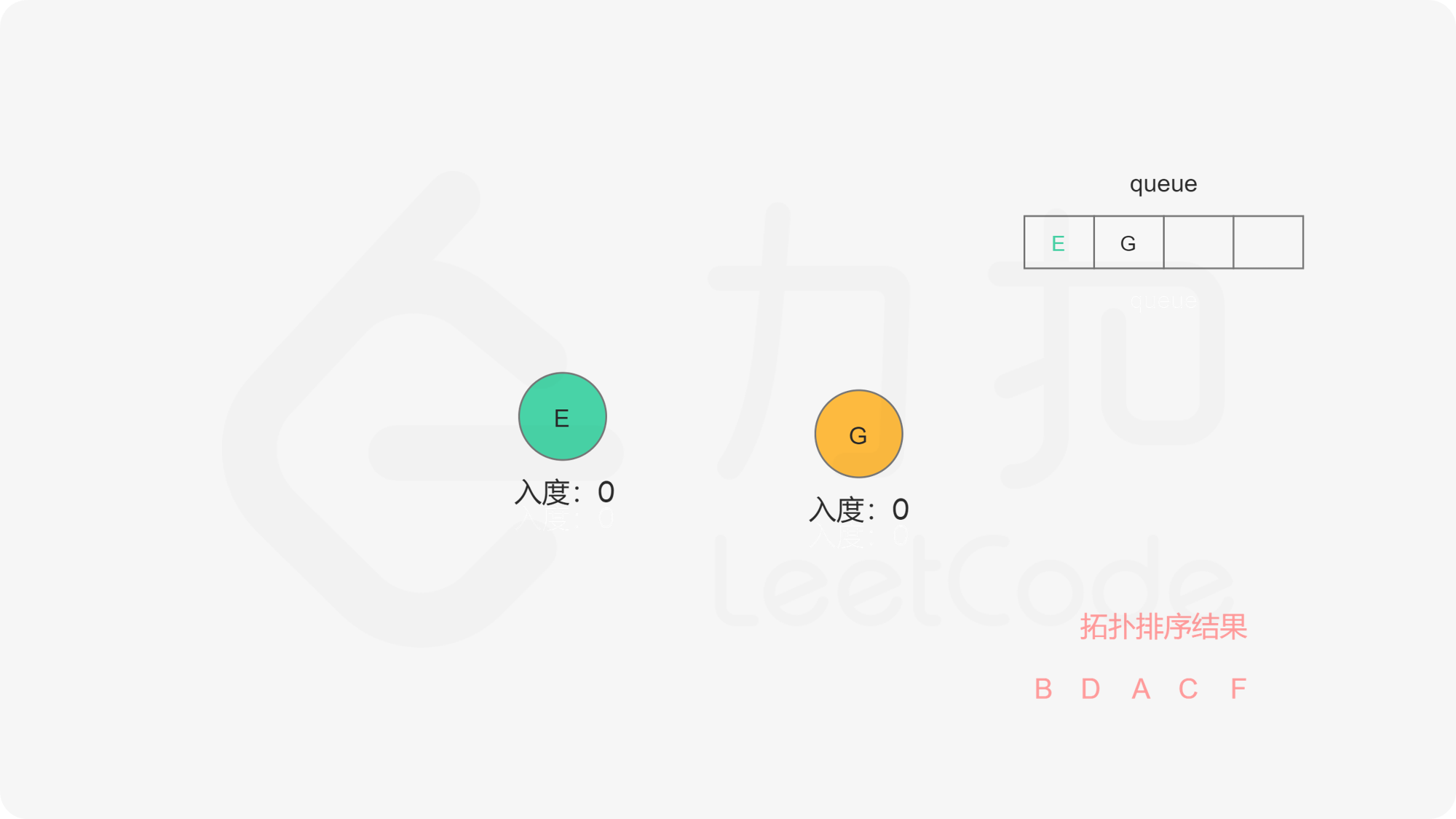
在广度优先搜索的每一步中，我们取出队首的节点 $u$：

  • 我们将 $u$ 放入答案中；

  • 我们移除 $u$ 的所有出边，也就是将 $u$ 的所有相邻节点的入度减少 $1$。如果某个相邻节点 $v$ 的入度变为 $0$，那么我们就将 $v$ 放入队列中。

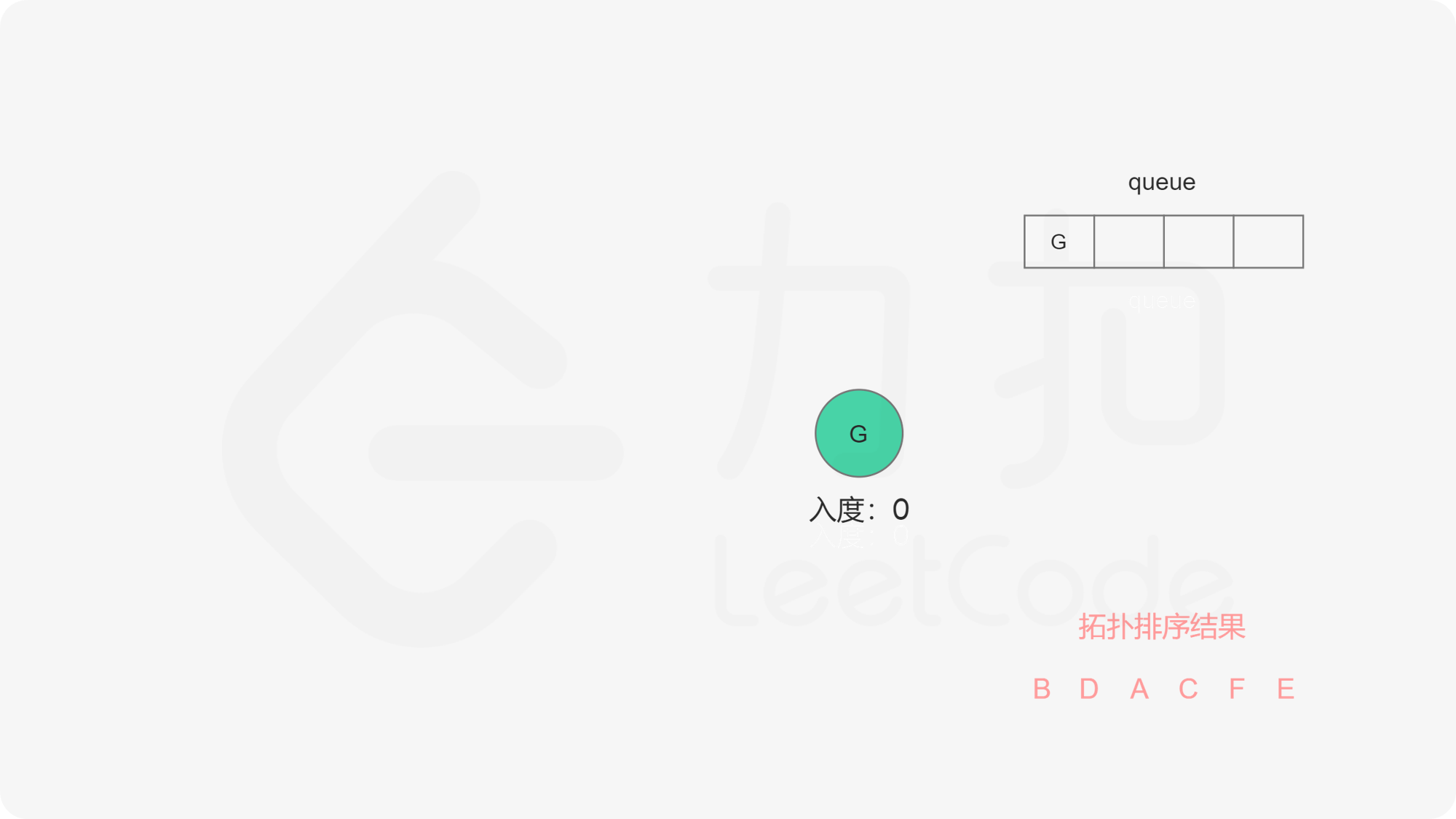
在广度优先搜索的过程结束后。如果答案中包含了这 $n$ 个节点，那么我们就找到了一种拓扑排序，否则说明图中存在环，也就不存在拓扑排序了。

下面的幻灯片给出了广度优先搜索的可视化流程。

<BFS1,BFS2,BFS3,BFS4,BFS5,BFS6,BFS7,BFS8,BFS9,BFS10,BFS11,BFS12,BFS13,BFS14>

[sol2-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
private:
    // 存储有向图
    vector<vector<int>> edges;
    // 存储每个节点的入度
    vector<int> indeg;
    // 存储答案
    vector<int> result;

public:
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        edges.resize(numCourses);
        indeg.resize(numCourses);
        for (const auto& info: prerequisites) {
            edges[info[1]].push_back(info[0]);
            ++indeg[info[0]];
        }

        queue<int> q;
        // 将所有入度为 0 的节点放入队列中
        for (int i = 0; i < numCourses; ++i) {
            if (indeg[i] == 0) {
                q.push(i);
            }
        }

        while (!q.empty()) {
            // 从队首取出一个节点
            int u = q.front();
            q.pop();
            // 放入答案中
            result.push_back(u);
            for (int v: edges[u]) {
                --indeg[v];
                // 如果相邻节点 v 的入度为 0，就可以选 v 对应的课程了
                if (indeg[v] == 0) {
                    q.push(v);
                }
            }
        }

        if (result.size() != numCourses) {
            return {};
        }
        return result;
    }
};
[sol2-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class Solution {
    // 存储有向图
    List<List<Integer>> edges;
    // 存储每个节点的入度
    int[] indeg;
    // 存储答案
    int[] result;
    // 答案下标
    int index;

    public int[] findOrder(int numCourses, int[][] prerequisites) {
        edges = new ArrayList<List<Integer>>();
        for (int i = 0; i < numCourses; ++i) {
            edges.add(new ArrayList<Integer>());
        }
        indeg = new int[numCourses];
        result = new int[numCourses];
        index = 0;
        for (int[] info : prerequisites) {
            edges.get(info[1]).add(info[0]);
            ++indeg[info[0]];
        }

        Queue<Integer> queue = new LinkedList<Integer>();
        // 将所有入度为 0 的节点放入队列中
        for (int i = 0; i < numCourses; ++i) {
            if (indeg[i] == 0) {
                queue.offer(i);
            }
        }

        while (!queue.isEmpty()) {
            // 从队首取出一个节点
            int u = queue.poll();
            // 放入答案中
            result[index++] = u;
            for (int v: edges.get(u)) {
                --indeg[v];
                // 如果相邻节点 v 的入度为 0，就可以选 v 对应的课程了
                if (indeg[v] == 0) {
                    queue.offer(v);
                }
            }
        }

        if (index != numCourses) {
            return new int[0];
        }
        return result;
    }
}
[sol2-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution:
    def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:
        # 存储有向图
        edges = collections.defaultdict(list)
        # 存储每个节点的入度
        indeg = [0] * numCourses
        # 存储答案
        result = list()

        for info in prerequisites:
            edges[info[1]].append(info[0])
            indeg[info[0]] += 1
        
        # 将所有入度为 0 的节点放入队列中
        q = collections.deque([u for u in range(numCourses) if indeg[u] == 0])

        while q:
            # 从队首取出一个节点
            u = q.popleft()
            # 放入答案中
            result.append(u)
            for v in edges[u]:
                indeg[v] -= 1
                # 如果相邻节点 v 的入度为 0，就可以选 v 对应的课程了
                if indeg[v] == 0:
                    q.append(v)

        if len(result) != numCourses:
            result = list()
        return result
[sol2-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
func findOrder(numCourses int, prerequisites [][]int) []int {
    var (
        edges = make([][]int, numCourses)
        indeg = make([]int, numCourses)
        result []int
    )

    for _, info := range prerequisites {
        edges[info[1]] = append(edges[info[1]], info[0])
        indeg[info[0]]++
    }

    q := []int{}
    for i := 0; i < numCourses; i++ {
        if indeg[i] == 0 {
            q = append(q, i)
        }
    }

    for len(q) > 0 {
        u := q[0]
        q = q[1:]
        result = append(result, u)
        for _, v := range edges[u] {
            indeg[v]--
            if indeg[v] == 0 {
                q = append(q, v)
            }
        }
    }
    if len(result) != numCourses {
        return []int{}
    }
    return result
}
[sol2-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
int* findOrder(int numCourses, int** prerequisites, int prerequisitesSize, int* prerequisitesColSize, int* returnSize) {
    int** edges = (int**)malloc(sizeof(int*) * numCourses);
    for (int i = 0; i < numCourses; i++) {
        edges[i] = (int*)malloc(0);
    }
    int edgeColSize[numCourses];
    memset(edgeColSize, 0, sizeof(edgeColSize));
    int indeg[numCourses];
    memset(indeg, 0, sizeof(indeg));
    for (int i = 0; i < prerequisitesSize; ++i) {
        int a = prerequisites[i][1], b = prerequisites[i][0];
        edgeColSize[a]++;
        edges[a] = (int*)realloc(edges[a], sizeof(int) * edgeColSize[a]);
        edges[a][edgeColSize[a] - 1] = b;
        ++indeg[b];
    }

    int q[numCourses];
    int l = 0, r = -1;
    for (int i = 0; i < numCourses; ++i) {
        if (indeg[i] == 0) {
            q[++r] = i;
        }
    }

    int* result = (int*)malloc(sizeof(int) * numCourses);
    int resultSize = 0;

    int visited = 0;
    while (l <= r) {
        ++visited;
        int u = q[l++];
        result[resultSize++] = u;
        for (int i = 0; i < edgeColSize[u]; ++i) {
            --indeg[edges[u][i]];
            if (indeg[edges[u][i]] == 0) {
                q[++r] = edges[u][i];
            }
        }
    }
    for (int i = 0; i < numCourses; i++) {
        free(edges[i]);
    }
    free(edges);
    if (visited == numCourses) {
        *returnSize = numCourses;
    } else {
        *returnSize = 0;
    }
    return result;
}

复杂度分析

  • 时间复杂度: $O(n+m)$，其中 $n$ 为课程数，$m$ 为先修课程的要求数。这其实就是对图进行广度优先搜索的时间复杂度。

  • 空间复杂度: $O(n+m)$。题目中是以列表形式给出的先修课程关系，为了对图进行广度优先搜索，我们需要存储成邻接表的形式，空间复杂度为 $O(n+m)$。在广度优先搜索的过程中，我们需要最多 $O(n)$ 的队列空间（迭代）进行广度优先搜索，并且还需要若干个 $O(n)$ 的空间存储节点入度、最终答案等。

 Comments
On this page
0210-课程表 II
  1. 📺 视频题解
  2. 📖 文字题解