给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。
示例 1:
**输入:** head = [1,2,2,1]
**输出:** true
示例 2:
**输入:** head = [1,2]
**输出:** false
提示:
链表中节点数目在范围[1, 105] 内
0 <= Node.val <= 9
进阶: 你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题?
方法一:将值复制到数组中后用双指针法 思路
如果你还不太熟悉链表,下面有关于列表的概要讲述。
有两种常用的列表实现,分别为数组列表和链表。如果我们想在列表中存储值,它们是如何实现的呢?
数组列表底层是使用数组存储值,我们可以通过索引在 $O(1)$ 的时间访问列表任何位置的值,这是由基于内存寻址的方式。
链表存储的是称为节点的对象,每个节点保存一个值和指向下一个节点的指针。访问某个特定索引的节点需要 $O(n)$ 的时间,因为要通过指针获取到下一个位置的节点。
确定数组列表是否回文很简单,我们可以使用双指针法来比较两端的元素,并向中间移动。一个指针从起点向中间移动,另一个指针从终点向中间移动。这需要 $O(n)$ 的时间,因为访问每个元素的时间是 $O(1)$,而有 $n$ 个元素要访问。
然而同样的方法在链表上操作并不简单,因为不论是正向访问还是反向访问都不是 $O(1)$。而将链表的值复制到数组列表中是 $O(n)$,因此最简单的方法就是将链表的值复制到数组列表中,再使用双指针法判断。
算法
一共为两个步骤:
复制链表值到数组列表中。
使用双指针法判断是否为回文。
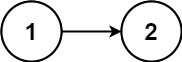
第一步,我们需要遍历链表将值复制到数组列表中。我们用 currentNode 指向当前节点。每次迭代向数组添加 currentNode.val,并更新 currentNode = currentNode.next,当 currentNode = null 时停止循环。
执行第二步的最佳方法取决于你使用的语言。在 Python 中,很容易构造一个列表的反向副本,也很容易比较两个列表。而在其他语言中,就没有那么简单。因此最好使用双指针法来检查是否为回文。我们在起点放置一个指针,在结尾放置一个指针,每一次迭代判断两个指针指向的元素是否相同,若不同,返回 false;相同则将两个指针向内移动,并继续判断,直到两个指针相遇。
在编码的过程中,注意我们比较的是节点值的大小,而不是节点本身。正确的比较方式是:node_1.val == node_2.val,而 node_1 == node_2 是错误的。
代码
[sol1-Python3] 1 2 3 4 5 6 7 8 class Solution : def isPalindrome (self, head: ListNode ) -> bool : vals = [] current_node = head while current_node is not None : vals.append(current_node.val) current_node = current_node.next return vals == vals[::-1 ]
[sol1-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution { public boolean isPalindrome (ListNode head) { List<Integer> vals = new ArrayList <Integer>(); ListNode currentNode = head; while (currentNode != null ) { vals.add(currentNode.val); currentNode = currentNode.next; } int front = 0 ; int back = vals.size() - 1 ; while (front < back) { if (!vals.get(front).equals(vals.get(back))) { return false ; } front++; back--; } return true ; } }
[sol1-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution {public : bool isPalindrome (ListNode* head) vector<int > vals; while (head != nullptr ) { vals.emplace_back (head->val); head = head->next; } for (int i = 0 , j = (int )vals.size () - 1 ; i < j; ++i, --j) { if (vals[i] != vals[j]) { return false ; } } return true ; } };
[sol1-JavaScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 var isPalindrome = function (head ) { const vals = []; while (head !== null ) { vals.push (head.val ); head = head.next ; } for (let i = 0 , j = vals.length - 1 ; i < j; ++i, --j) { if (vals[i] !== vals[j]) { return false ; } } return true ; };
[sol1-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 func isPalindrome (head *ListNode) bool { vals := []int {} for ; head != nil ; head = head.Next { vals = append (vals, head.Val) } n := len (vals) for i, v := range vals[:n/2 ] { if v != vals[n-1 -i] { return false } } return true }
[sol1-C] 1 2 3 4 5 6 7 8 9 10 11 12 13 bool isPalindrome (struct ListNode* head) { int vals[50001 ], vals_num = 0 ; while (head != NULL ) { vals[vals_num++] = head->val; head = head->next; } for (int i = 0 , j = vals_num - 1 ; i < j; ++i, --j) { if (vals[i] != vals[j]) { return false ; } } return true ; }
复杂度分析
时间复杂度:$O(n)$,其中 $n$ 指的是链表的元素个数。
第一步: 遍历链表并将值复制到数组中,$O(n)$。
第二步:双指针判断是否为回文,执行了 $O(n/2)$ 次的判断,即 $O(n)$。
总的时间复杂度:$O(2n) = O(n)$。
空间复杂度:$O(n)$,其中 $n$ 指的是链表的元素个数,我们使用了一个数组列表存放链表的元素值。
方法二:递归 思路
为了想出使用空间复杂度为 $O(1)$ 的算法,你可能想过使用递归来解决,但是这仍然需要 $O(n)$ 的空间复杂度。
递归为我们提供了一种优雅的方式来方向遍历节点。
1 2 3 4 function print_values_in_reverse(ListNode head) if head is NOT null print_values_in_reverse(head.next) print head.val
如果使用递归反向迭代节点,同时使用递归函数外的变量向前迭代,就可以判断链表是否为回文。
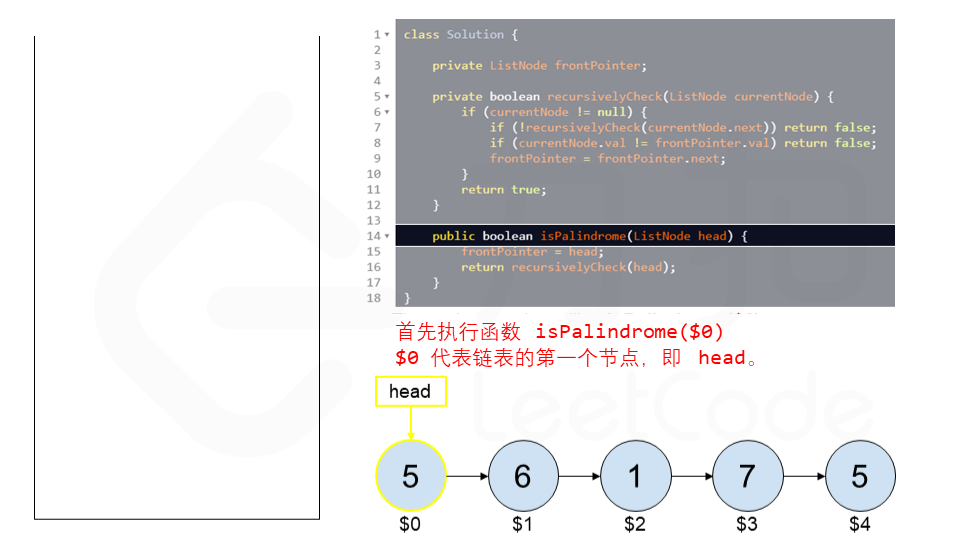
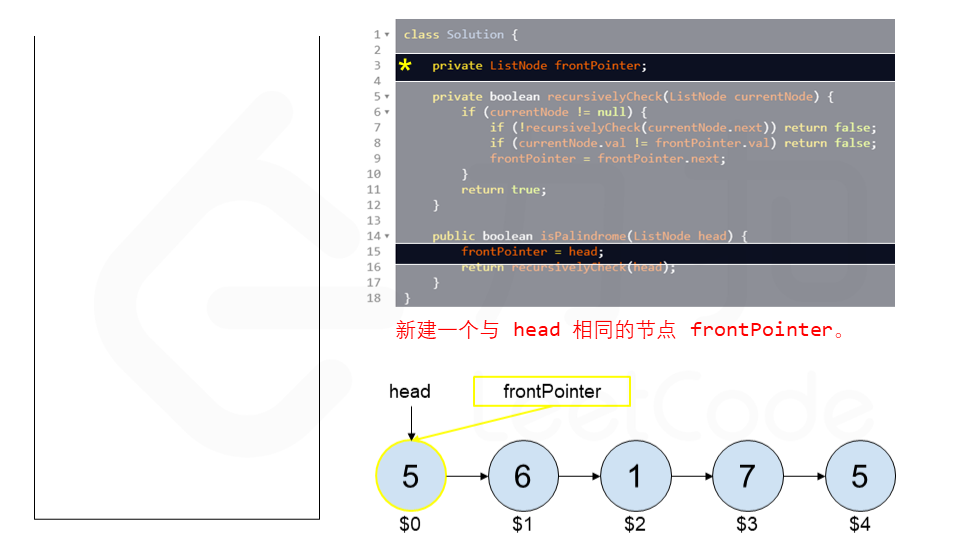
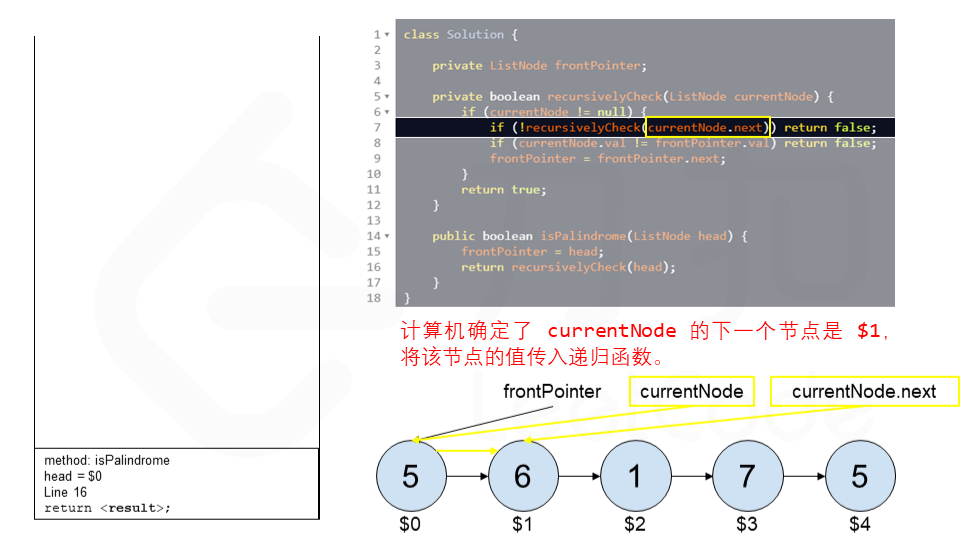
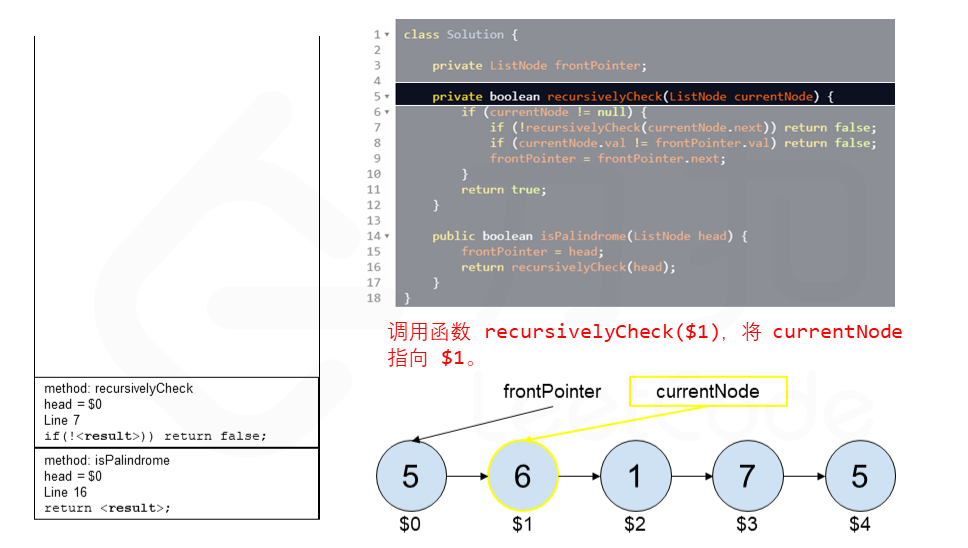
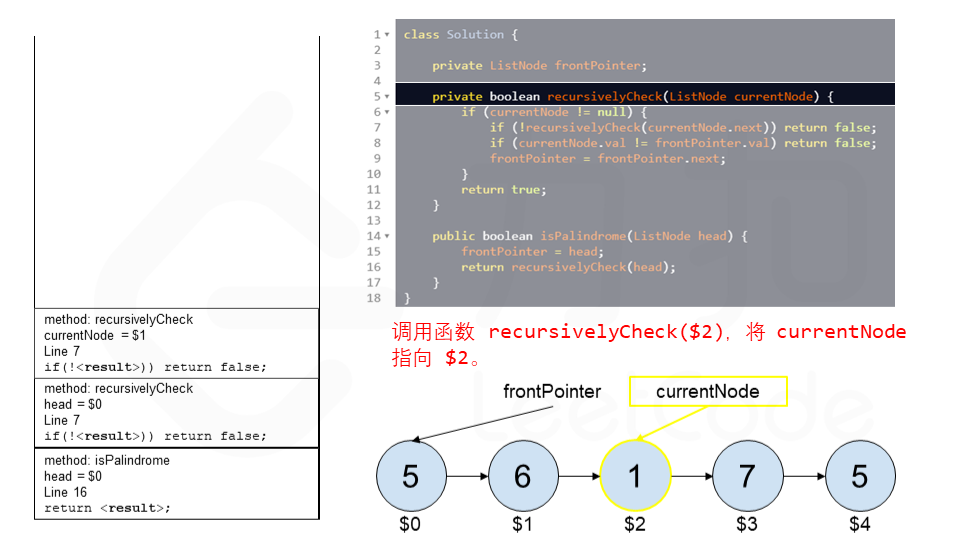
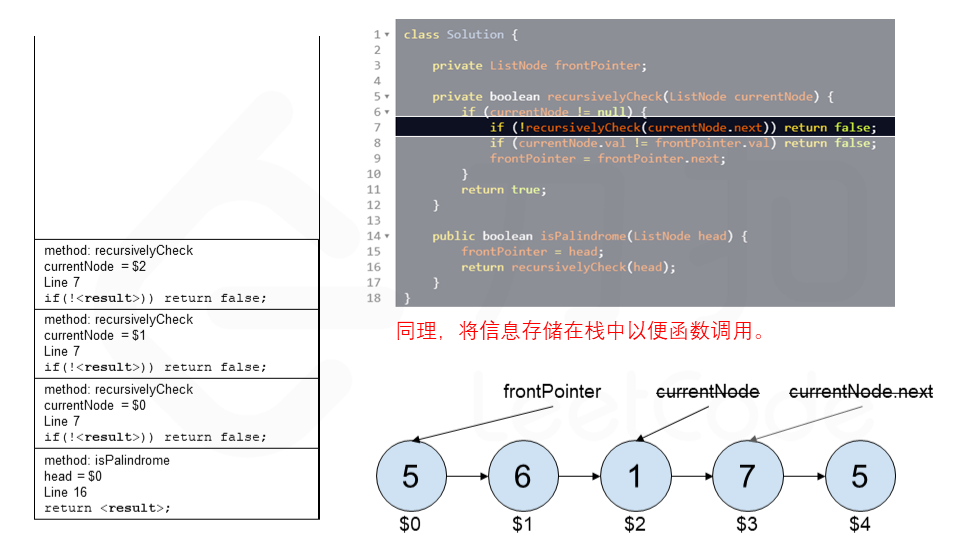
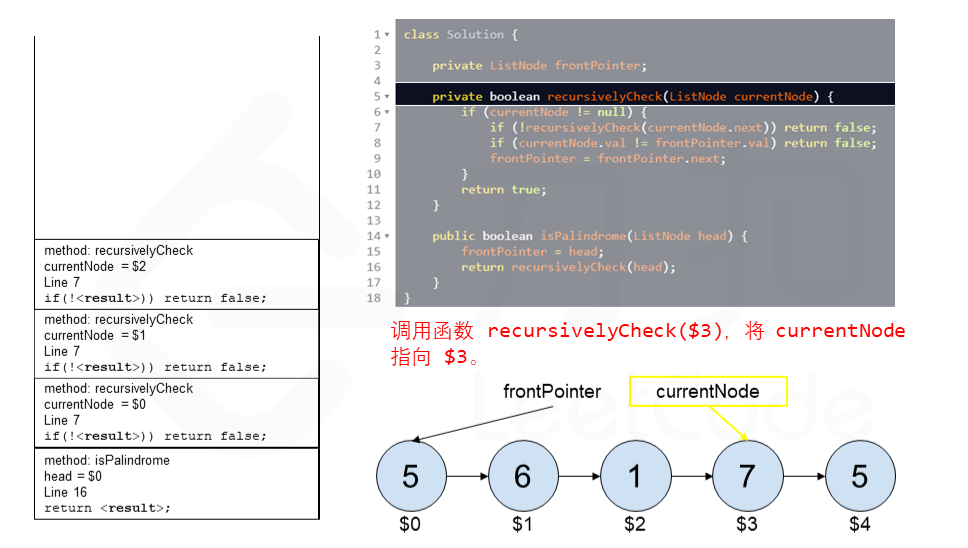
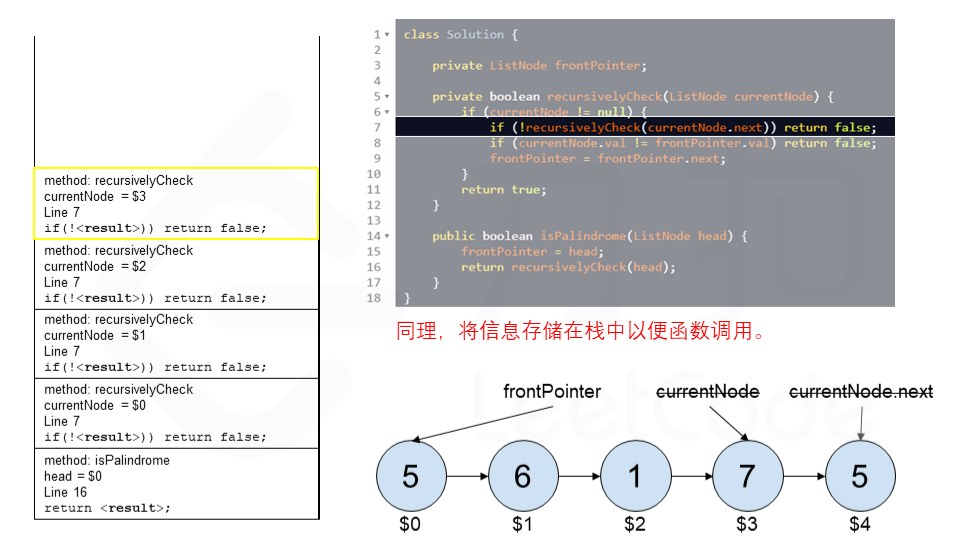
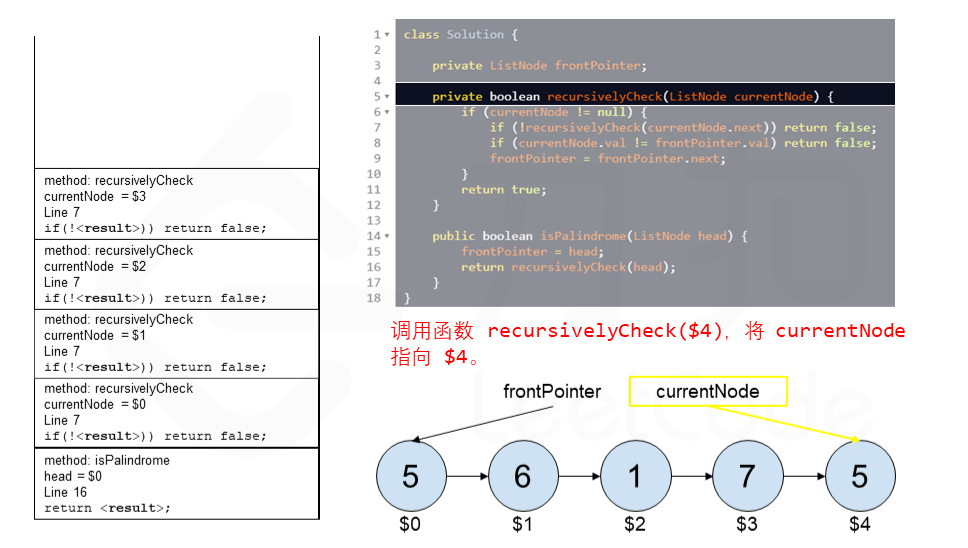
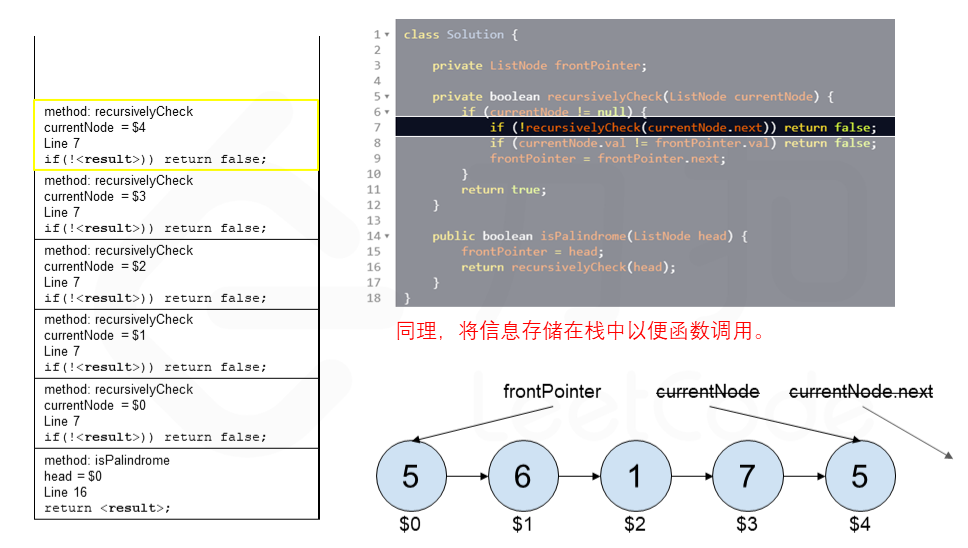
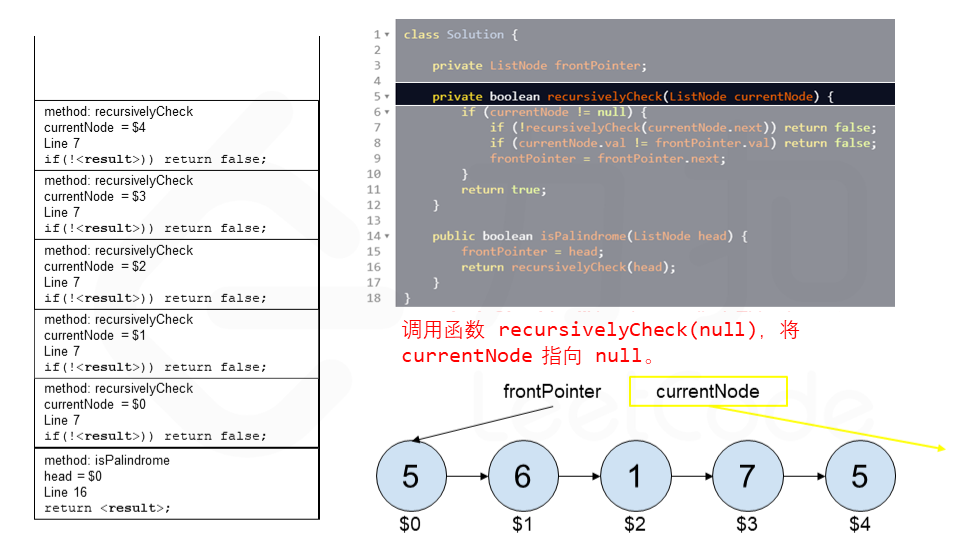
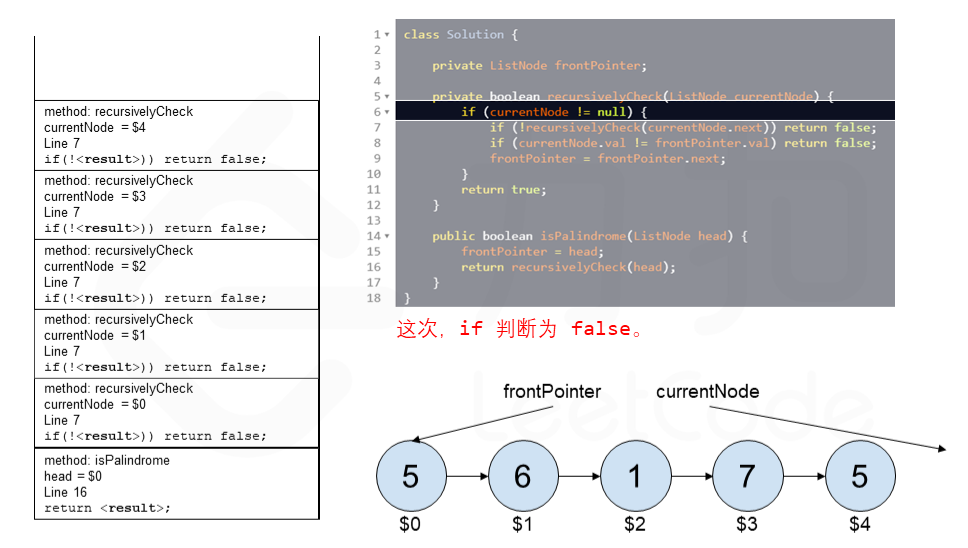
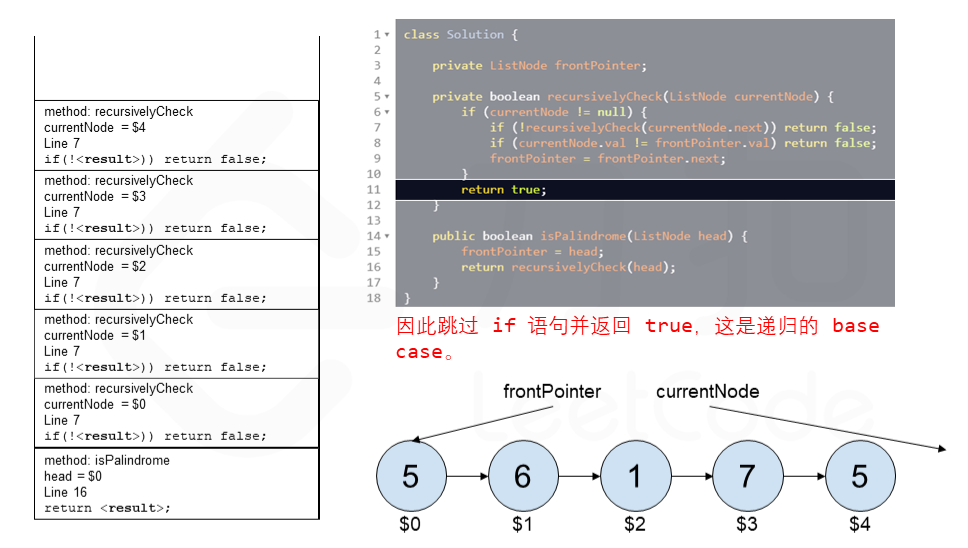
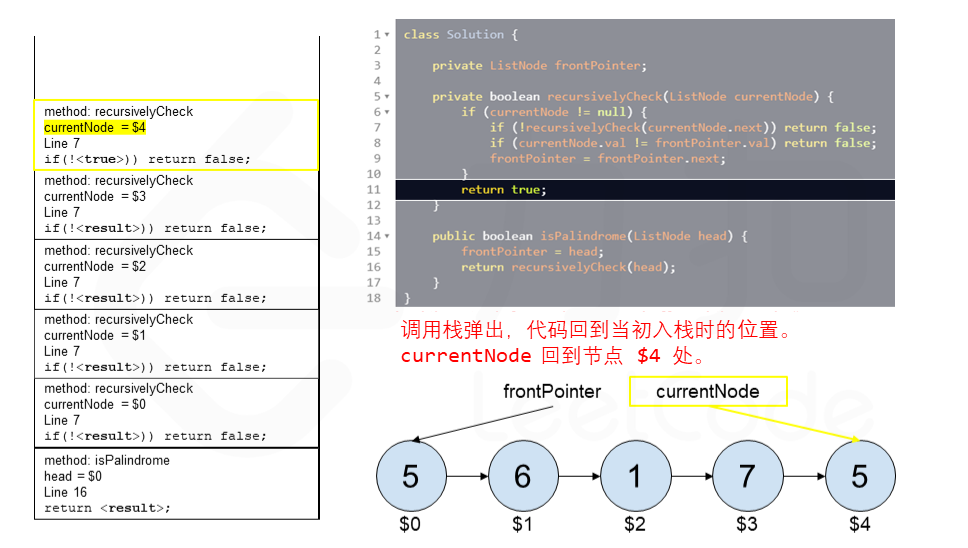
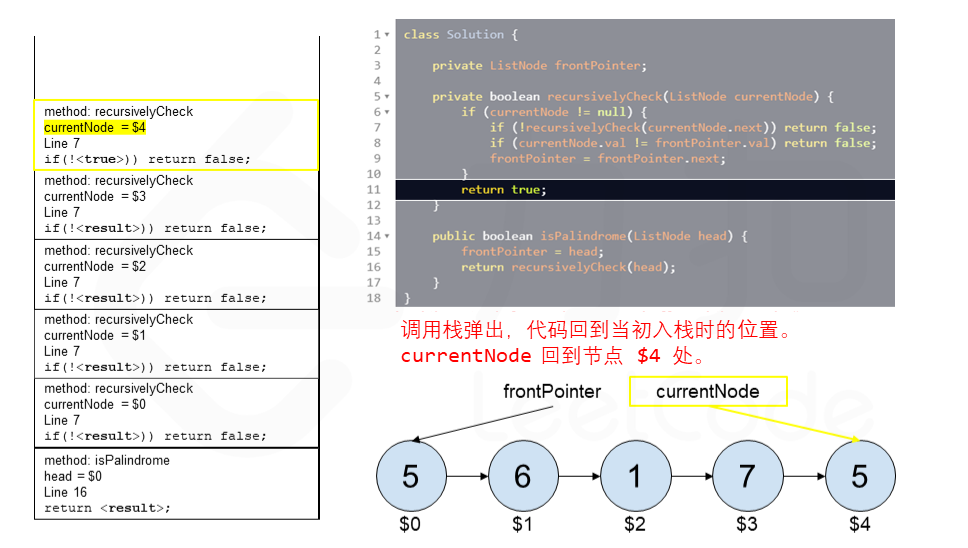
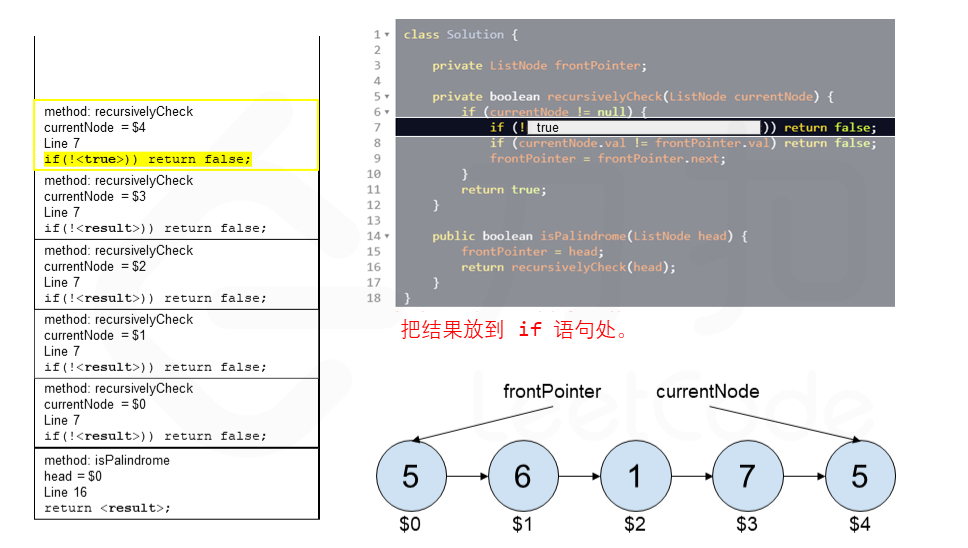
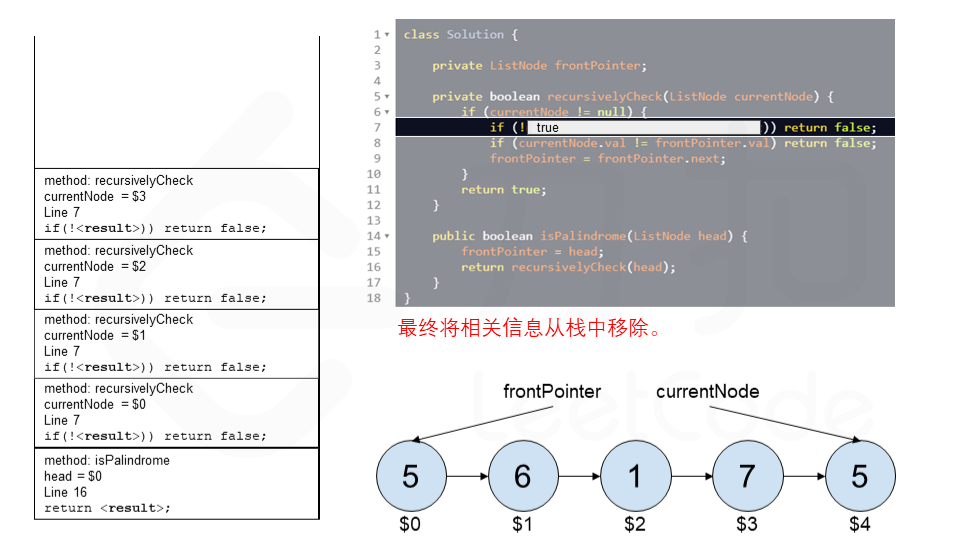
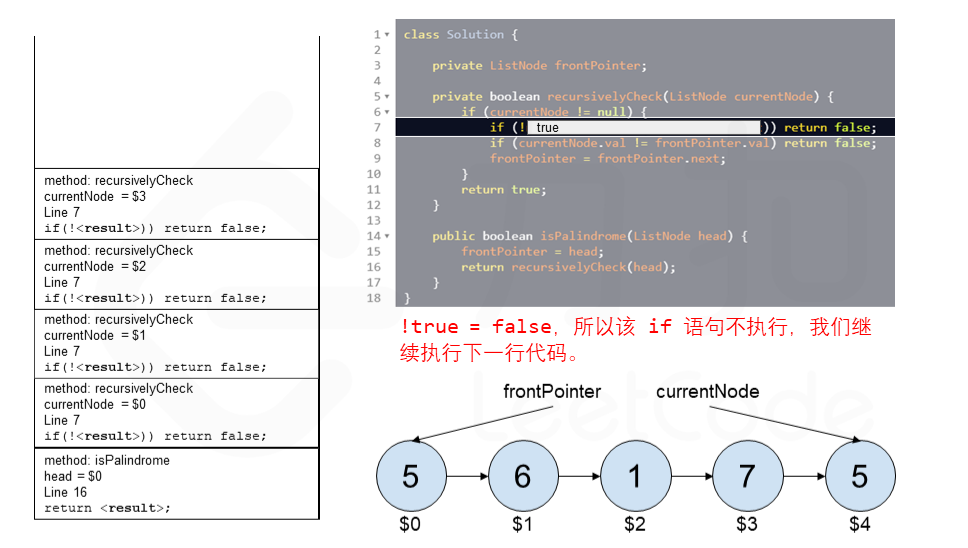
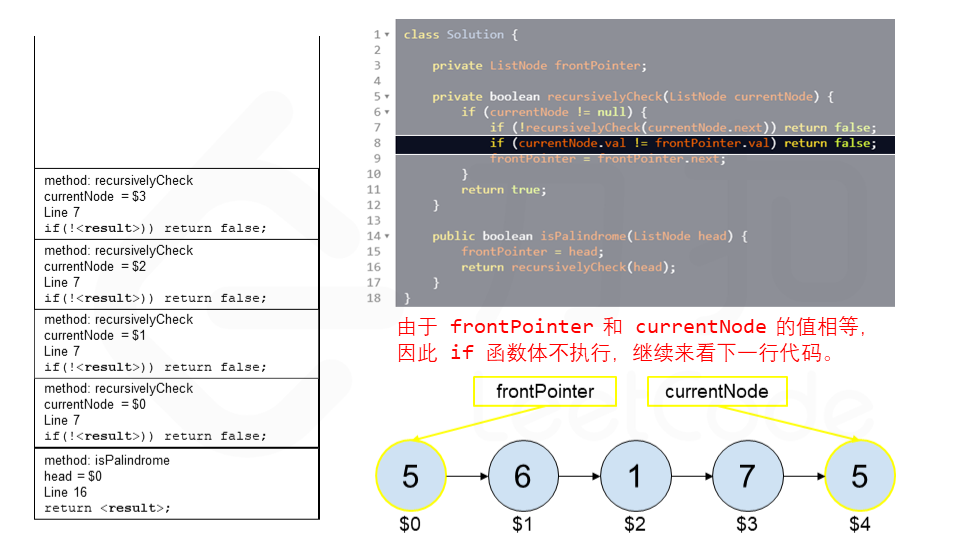
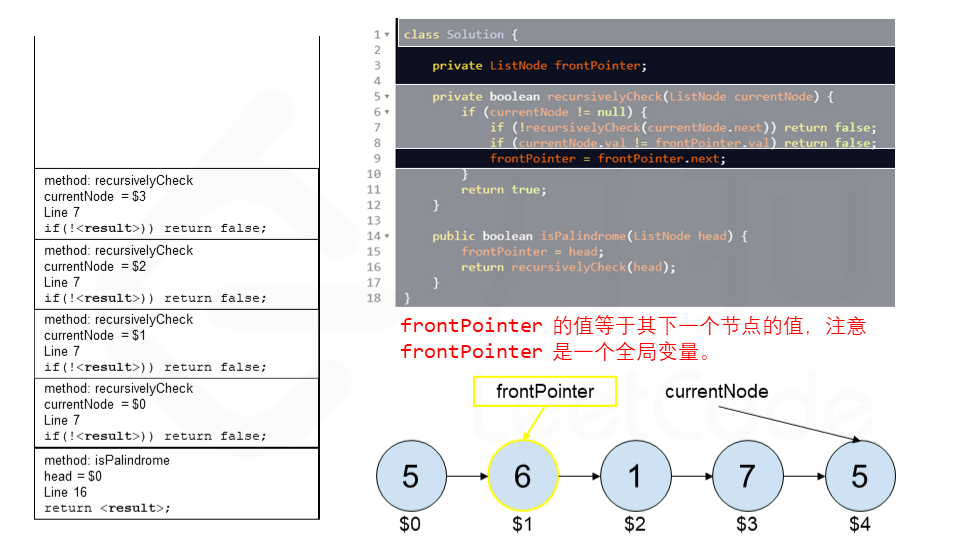
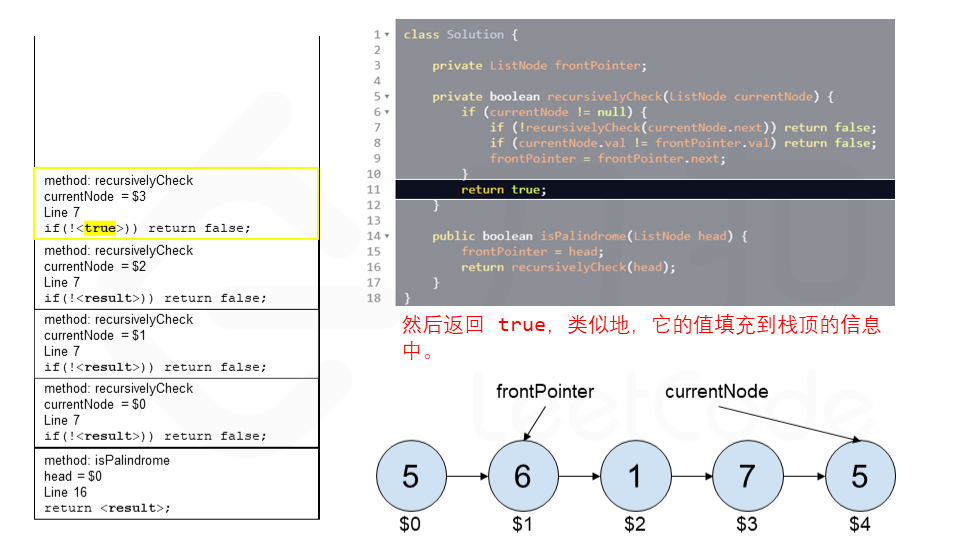
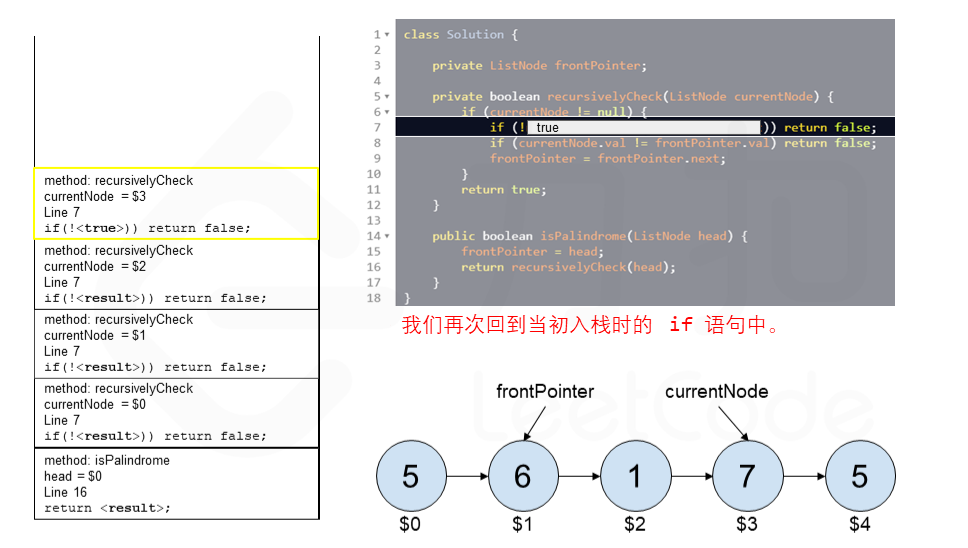
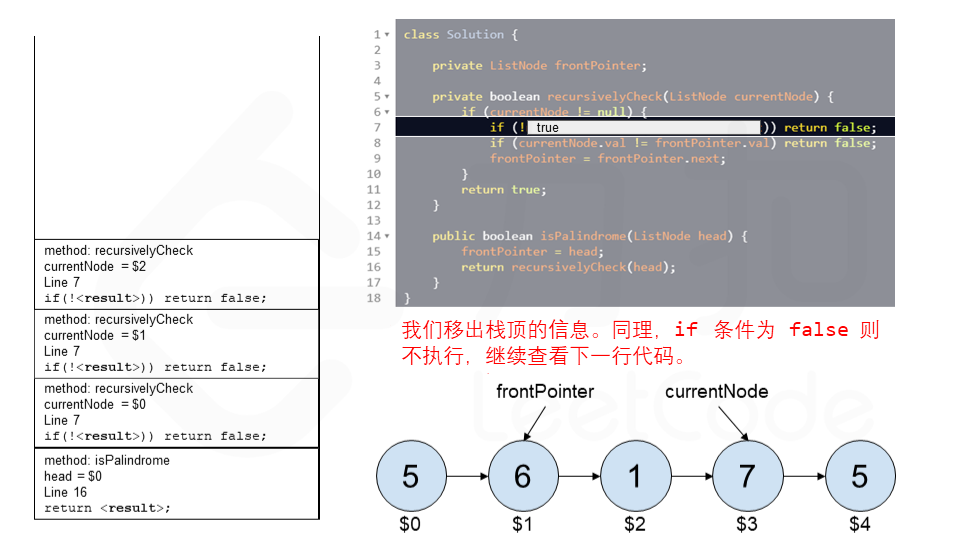
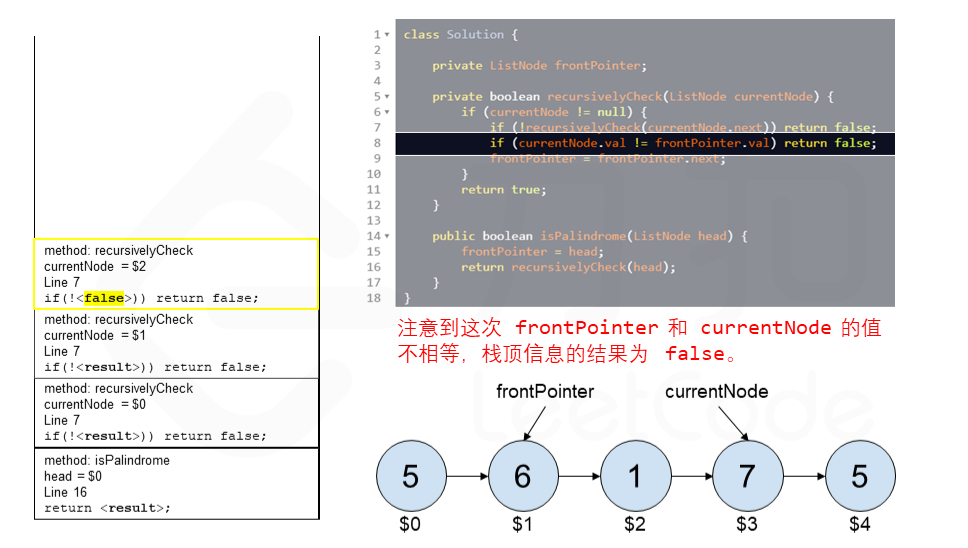
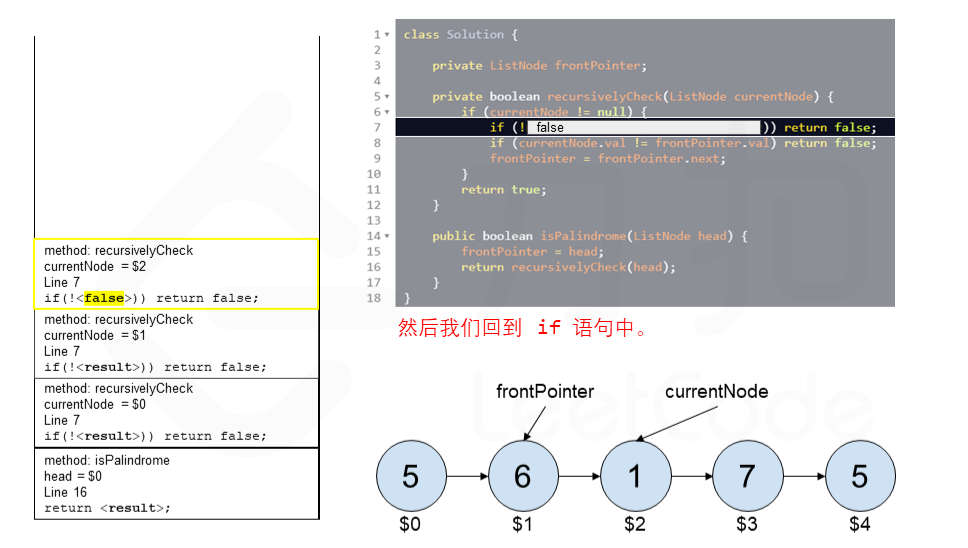
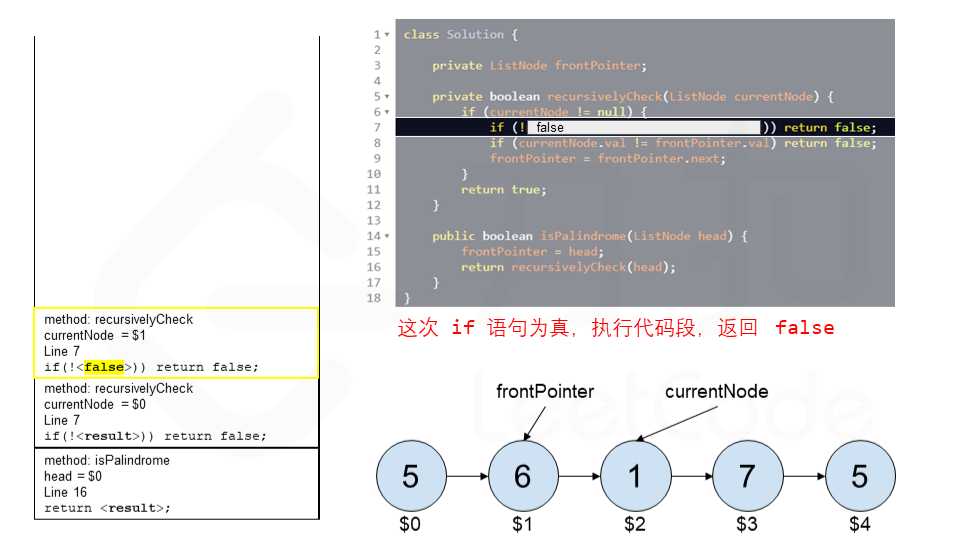
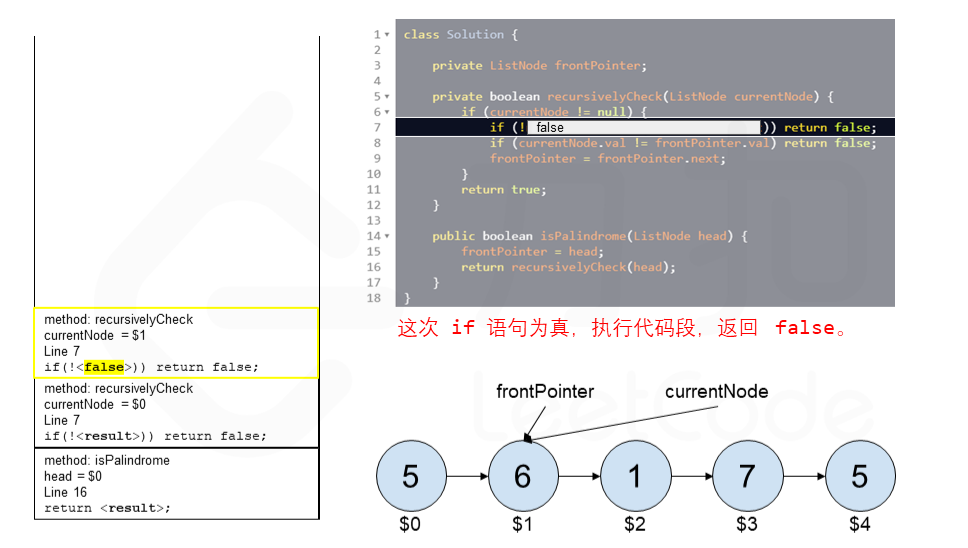
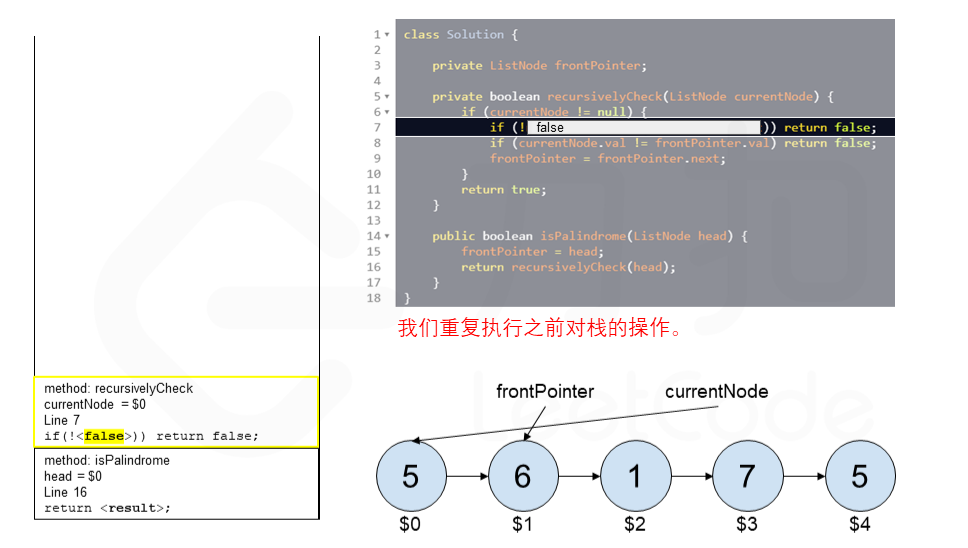
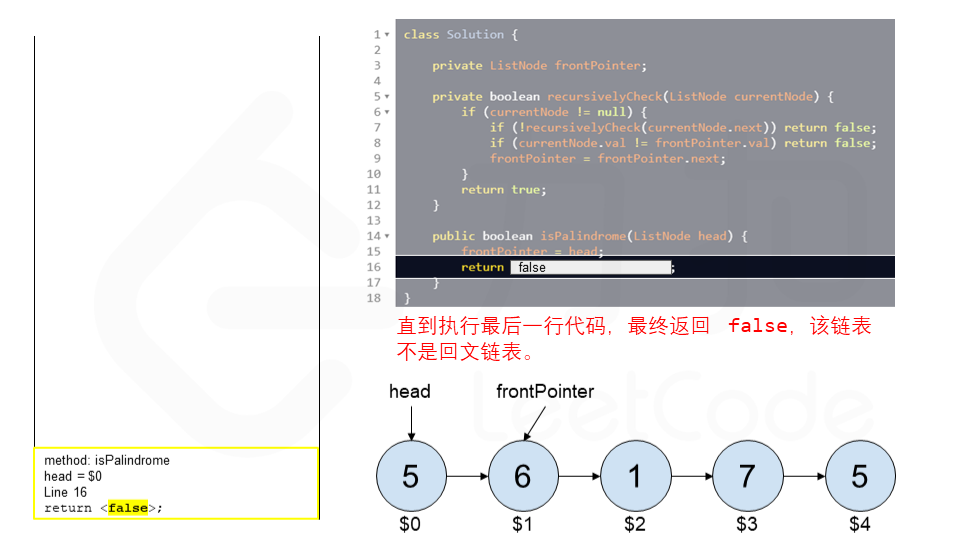
算法 currentNode 指针是先到尾节点,由于递归的特性再从后往前进行比较。frontPointer 是递归函数外的指针。若 currentNode.val != frontPointer.val 则返回 false。反之,frontPointer 向前移动并返回 true。
算法的正确性在于递归处理节点的顺序是相反的(回顾上面打印的算法),而我们在函数外又记录了一个变量,因此从本质上,我们同时在正向和逆向迭代匹配。
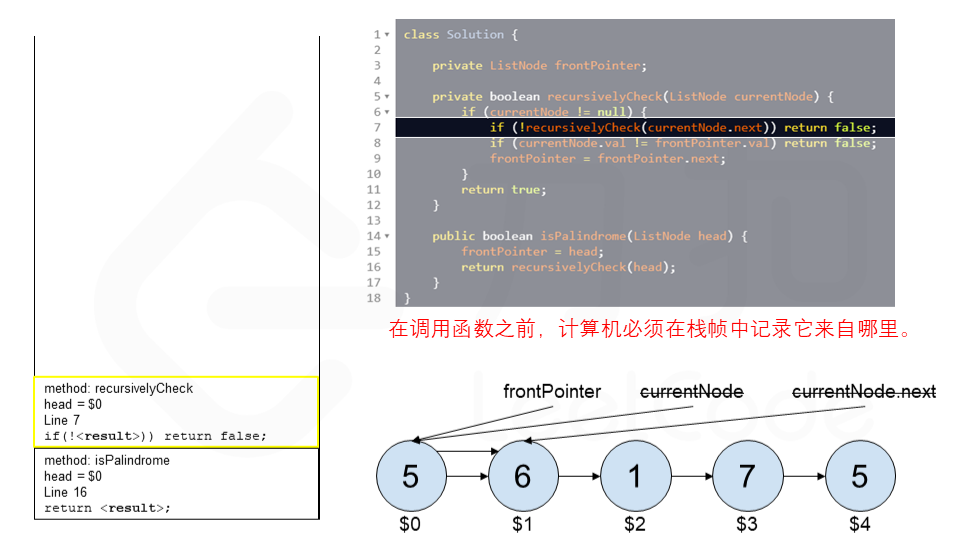
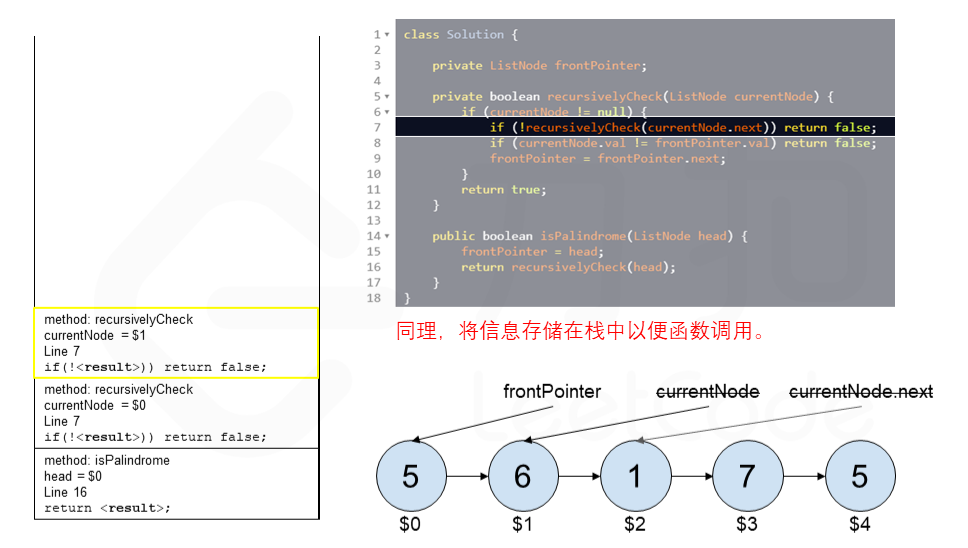
下面的动画展示了算法的工作原理。我们定义递归函数名字为 recursively_check,每个节点都被赋予了标识符(如 $1)以便更好地解释它们。计算机在递归的过程中将使用堆栈的空间,这就是为什么递归并不是 $O(1)$ 的空间复杂度。
<
代码
[sol2-Python3] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution : def isPalindrome (self, head: ListNode ) -> bool : self.front_pointer = head def recursively_check (current_node=head ): if current_node is not None : if not recursively_check(current_node.next ): return False if self.front_pointer.val != current_node.val: return False self.front_pointer = self.front_pointer.next return True return recursively_check()
[sol2-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution { private ListNode frontPointer; private boolean recursivelyCheck (ListNode currentNode) { if (currentNode != null ) { if (!recursivelyCheck(currentNode.next)) { return false ; } if (currentNode.val != frontPointer.val) { return false ; } frontPointer = frontPointer.next; } return true ; } public boolean isPalindrome (ListNode head) { frontPointer = head; return recursivelyCheck(head); } }
[sol2-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution { ListNode* frontPointer; public : bool recursivelyCheck (ListNode* currentNode) if (currentNode != nullptr ) { if (!recursivelyCheck (currentNode->next)) { return false ; } if (currentNode->val != frontPointer->val) { return false ; } frontPointer = frontPointer->next; } return true ; } bool isPalindrome (ListNode* head) frontPointer = head; return recursivelyCheck (head); } };
[sol2-JavaScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 let frontPointer;const recursivelyCheck = (currentNode ) => { if (currentNode !== null ) { if (!recursivelyCheck (currentNode.next )) { return false ; } if (currentNode.val !== frontPointer.val ) { return false ; } frontPointer = frontPointer.next ; } return true ; } var isPalindrome = function (head ) { frontPointer = head; return recursivelyCheck (head); };
[sol2-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 func isPalindrome (head *ListNode) bool { frontPointer := head var recursivelyCheck func (*ListNode) bool recursivelyCheck = func (curNode *ListNode) bool { if curNode != nil { if !recursivelyCheck(curNode.Next) { return false } if curNode.Val != frontPointer.Val { return false } frontPointer = frontPointer.Next } return true } return recursivelyCheck(head) }
[sol2-C] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 struct ListNode * frontPointer ;bool recursivelyCheck (struct ListNode* currentNode) { if (currentNode != NULL ) { if (!recursivelyCheck(currentNode->next)) { return false ; } if (currentNode->val != frontPointer->val) { return false ; } frontPointer = frontPointer->next; } return true ; } bool isPalindrome (struct ListNode* head) { frontPointer = head; return recursivelyCheck(head); }
复杂度分析
时间复杂度:$O(n)$,其中 $n$ 指的是链表的大小。
空间复杂度:$O(n)$,其中 $n$ 指的是链表的大小。我们要理解计算机如何运行递归函数,在一个函数中调用一个函数时,计算机需要在进入被调用函数之前跟踪它在当前函数中的位置(以及任何局部变量的值),通过运行时存放在堆栈中来实现(堆栈帧)。在堆栈中存放好了数据后就可以进入被调用的函数。在完成被调用函数之后,他会弹出堆栈顶部元素,以恢复在进行函数调用之前所在的函数。在进行回文检查之前,递归函数将在堆栈中创建 $n$ 个堆栈帧,计算机会逐个弹出进行处理。所以在使用递归时空间复杂度要考虑堆栈的使用情况。
这种方法不仅使用了 $O(n)$ 的空间,且比第一种方法更差,因为在许多语言中,堆栈帧的开销很大(如 Python),并且最大的运行时堆栈深度为 1000(可以增加,但是有可能导致底层解释程序内存出错)。为每个节点创建堆栈帧极大的限制了算法能够处理的最大链表大小。
方法三:快慢指针 思路
避免使用 $O(n)$ 额外空间的方法就是改变输入。
我们可以将链表的后半部分反转(修改链表结构),然后将前半部分和后半部分进行比较。比较完成后我们应该将链表恢复原样。虽然不需要恢复也能通过测试用例,但是使用该函数的人通常不希望链表结构被更改。
该方法虽然可以将空间复杂度降到 $O(1)$,但是在并发环境下,该方法也有缺点。在并发环境下,函数运行时需要锁定其他线程或进程对链表的访问,因为在函数执行过程中链表会被修改。
算法
整个流程可以分为以下五个步骤:
找到前半部分链表的尾节点。
反转后半部分链表。
判断是否回文。
恢复链表。
返回结果。
执行步骤一,我们可以计算链表节点的数量,然后遍历链表找到前半部分的尾节点。
我们也可以使用快慢指针 在一次遍历中找到:慢指针一次走一步,快指针一次走两步,快慢指针同时出发。当快指针移动到链表的末尾时,慢指针恰好到链表的中间。通过慢指针将链表分为两部分。
若链表有奇数个节点,则中间的节点应该看作是前半部分。
步骤二可以使用「206. 反转链表 」问题中的解决方法来反转链表的后半部分。
步骤三比较两个部分的值,当后半部分到达末尾则比较完成,可以忽略计数情况中的中间节点。
步骤四与步骤二使用的函数相同,再反转一次恢复链表本身。
代码
[sol3-Python] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 class Solution : def isPalindrome (self, head: ListNode ) -> bool : if head is None : return True first_half_end = self.end_of_first_half(head) second_half_start = self.reverse_list(first_half_end.next ) result = True first_position = head second_position = second_half_start while result and second_position is not None : if first_position.val != second_position.val: result = False first_position = first_position.next second_position = second_position.next first_half_end.next = self.reverse_list(second_half_start) return result def end_of_first_half (self, head ): fast = head slow = head while fast.next is not None and fast.next .next is not None : fast = fast.next .next slow = slow.next return slow def reverse_list (self, head ): previous = None current = head while current is not None : next_node = current.next current.next = previous previous = current current = next_node return previous
[sol3-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 class Solution { public boolean isPalindrome (ListNode head) { if (head == null ) { return true ; } ListNode firstHalfEnd = endOfFirstHalf(head); ListNode secondHalfStart = reverseList(firstHalfEnd.next); ListNode p1 = head; ListNode p2 = secondHalfStart; boolean result = true ; while (result && p2 != null ) { if (p1.val != p2.val) { result = false ; } p1 = p1.next; p2 = p2.next; } firstHalfEnd.next = reverseList(secondHalfStart); return result; } private ListNode reverseList (ListNode head) { ListNode prev = null ; ListNode curr = head; while (curr != null ) { ListNode nextTemp = curr.next; curr.next = prev; prev = curr; curr = nextTemp; } return prev; } private ListNode endOfFirstHalf (ListNode head) { ListNode fast = head; ListNode slow = head; while (fast.next != null && fast.next.next != null ) { fast = fast.next.next; slow = slow.next; } return slow; } }
[sol3-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 class Solution {public : bool isPalindrome (ListNode* head) if (head == nullptr ) { return true ; } ListNode* firstHalfEnd = endOfFirstHalf (head); ListNode* secondHalfStart = reverseList (firstHalfEnd->next); ListNode* p1 = head; ListNode* p2 = secondHalfStart; bool result = true ; while (result && p2 != nullptr ) { if (p1->val != p2->val) { result = false ; } p1 = p1->next; p2 = p2->next; } firstHalfEnd->next = reverseList (secondHalfStart); return result; } ListNode* reverseList (ListNode* head) { ListNode* prev = nullptr ; ListNode* curr = head; while (curr != nullptr ) { ListNode* nextTemp = curr->next; curr->next = prev; prev = curr; curr = nextTemp; } return prev; } ListNode* endOfFirstHalf (ListNode* head) { ListNode* fast = head; ListNode* slow = head; while (fast->next != nullptr && fast->next->next != nullptr ) { fast = fast->next->next; slow = slow->next; } return slow; } };
[sol3-JavaScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 const reverseList = (head ) => { let prev = null ; let curr = head; while (curr !== null ) { let nextTemp = curr.next ; curr.next = prev; prev = curr; curr = nextTemp; } return prev; } const endOfFirstHalf = (head ) => { let fast = head; let slow = head; while (fast.next !== null && fast.next .next !== null ) { fast = fast.next .next ; slow = slow.next ; } return slow; } var isPalindrome = function (head ) { if (head == null ) return true ; const firstHalfEnd = endOfFirstHalf (head); const secondHalfStart = reverseList (firstHalfEnd.next ); let p1 = head; let p2 = secondHalfStart; let result = true ; while (result && p2 != null ) { if (p1.val != p2.val ) result = false ; p1 = p1.next ; p2 = p2.next ; } firstHalfEnd.next = reverseList (secondHalfStart); return result; };
[sol3-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 func reverseList (head *ListNode) var prev, cur *ListNode = nil , head for cur != nil { nextTmp := cur.Next cur.Next = prev prev = cur cur = nextTmp } return prev } func endOfFirstHalf (head *ListNode) fast := head slow := head for fast.Next != nil && fast.Next.Next != nil { fast = fast.Next.Next slow = slow.Next } return slow } func isPalindrome (head *ListNode) bool { if head == nil { return true } firstHalfEnd := endOfFirstHalf(head) secondHalfStart := reverseList(firstHalfEnd.Next) p1 := head p2 := secondHalfStart result := true for result && p2 != nil { if p1.Val != p2.Val { result = false } p1 = p1.Next p2 = p2.Next } firstHalfEnd.Next = reverseList(secondHalfStart) return result }
[sol3-C] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 struct ListNode* reverseList (struct ListNode* head) { struct ListNode * prev =NULL ; struct ListNode * curr = while (curr != NULL ) { struct ListNode * nextTemp = curr->next = prev; prev = curr; curr = nextTemp; } return prev; } struct ListNode* endOfFirstHalf (struct ListNode* head) { struct ListNode * fast = struct ListNode * slow = while (fast->next != NULL && fast->next->next != NULL ) { fast = fast->next->next; slow = slow->next; } return slow; } bool isPalindrome (struct ListNode* head) { if (head == NULL ) { return true ; } struct ListNode * firstHalfEnd = struct ListNode * secondHalfStart = struct ListNode * p1 = struct ListNode * p2 = bool result = true ; while (result && p2 != NULL ) { if (p1->val != p2->val) { result = false ; } p1 = p1->next; p2 = p2->next; } firstHalfEnd->next = reverseList(secondHalfStart); return result; }
复杂度分析