0235-二叉搜索树的最近公共祖先

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 10:44:22 2023-09-13 10:44:22 Updated    

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科 中最近公共祖先的定义为：”对于有根树
T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（ 一个节点也可以是它自己的祖先 ）。”

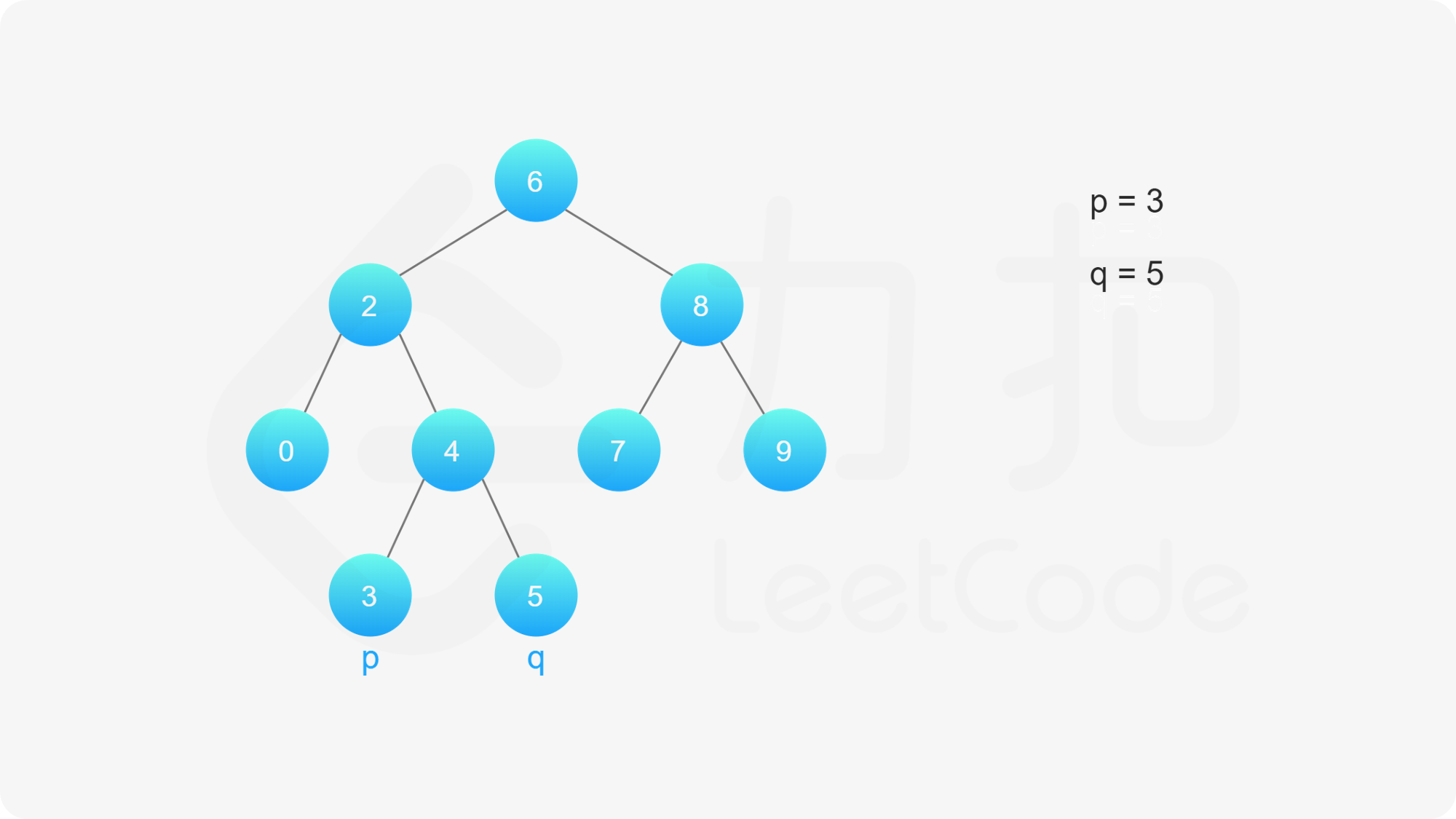
例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2018/12/14/binarysearchtree_improved.png)

示例 1:

**输入:** root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
**输出:** 6 
**解释:** 节点 2 和节点 8 的最近公共祖先是 6。

示例 2:

**输入:** root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
**输出:** 2
**解释:** 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

  • 所有节点的值都是唯一的。
  • p、q 为不同节点且均存在于给定的二叉搜索树中。

方法一：两次遍历

思路与算法

注意到题目中给出的是一棵「二叉搜索树」，因此我们可以快速地找出树中的某个节点以及从根节点到该节点的路径，例如我们需要找到节点 $p$：

  • 我们从根节点开始遍历；

  • 如果当前节点就是 $p$，那么成功地找到了节点；

  • 如果当前节点的值大于 $p$ 的值，说明 $p$ 应该在当前节点的左子树，因此将当前节点移动到它的左子节点；

  • 如果当前节点的值小于 $p$ 的值，说明 $p$ 应该在当前节点的右子树，因此将当前节点移动到它的右子节点。

对于节点 $q$ 同理。在寻找节点的过程中，我们可以顺便记录经过的节点，这样就得到了从根节点到被寻找节点的路径。

当我们分别得到了从根节点到 $p$ 和 $q$ 的路径之后，我们就可以很方便地找到它们的最近公共祖先了。显然，$p$ 和 $q$ 的最近公共祖先就是从根节点到它们路径上的「分岔点」，也就是最后一个相同的节点。因此，如果我们设从根节点到 $p$ 的路径为数组 $\textit{path_p}$，从根节点到 $q$ 的路径为数组 $\textit{path_q}$，那么只要找出最大的编号 $i$，其满足

$$
\textit{path_p}[i] = \textit{path_q}[i]
$$

那么对应的节点就是「分岔点」，即 $p$ 和 $q$ 的最近公共祖先就是 $\textit{path_p}[i]$（或 $\textit{path_q}[i]$）。

代码

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    vector<TreeNode*> getPath(TreeNode* root, TreeNode* target) {
        vector<TreeNode*> path;
        TreeNode* node = root;
        while (node != target) {
            path.push_back(node);
            if (target->val < node->val) {
                node = node->left;
            }
            else {
                node = node->right;
            }
        }
        path.push_back(node);
        return path;
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        vector<TreeNode*> path_p = getPath(root, p);
        vector<TreeNode*> path_q = getPath(root, q);
        TreeNode* ancestor;
        for (int i = 0; i < path_p.size() && i < path_q.size(); ++i) {
            if (path_p[i] == path_q[i]) {
                ancestor = path_p[i];
            }
            else {
                break;
            }
        }
        return ancestor;
    }
};
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        List<TreeNode> path_p = getPath(root, p);
        List<TreeNode> path_q = getPath(root, q);
        TreeNode ancestor = null;
        for (int i = 0; i < path_p.size() && i < path_q.size(); ++i) {
            if (path_p.get(i) == path_q.get(i)) {
                ancestor = path_p.get(i);
            } else {
                break;
            }
        }
        return ancestor;
    }

    public List<TreeNode> getPath(TreeNode root, TreeNode target) {
        List<TreeNode> path = new ArrayList<TreeNode>();
        TreeNode node = root;
        while (node != target) {
            path.add(node);
            if (target.val < node.val) {
                node = node.left;
            } else {
                node = node.right;
            }
        }
        path.add(node);
        return path;
    }
}
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution:
    def lowestCommonAncestor(self, root: TreeNode, p: TreeNode, q: TreeNode) -> TreeNode:
        def getPath(root: TreeNode, target: TreeNode) -> List[TreeNode]:
            path = list()
            node = root
            while node != target:
                path.append(node)
                if target.val < node.val:
                    node = node.left
                else:
                    node = node.right
            path.append(node)
            return path
        
        path_p = getPath(root, p)
        path_q = getPath(root, q)
        ancestor = None
        for u, v in zip(path_p, path_q):
            if u == v:
                ancestor = u
            else:
                break
        
        return ancestor
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
func getPath(root, target *TreeNode) (path []*TreeNode) {
    node := root
    for node != target {
        path = append(path, node)
        if target.Val < node.Val {
            node = node.Left
        } else {
            node = node.Right
        }
    }
    path = append(path, node)
    return
}

func lowestCommonAncestor(root, p, q *TreeNode) (ancestor *TreeNode) {
    pathP := getPath(root, p)
    pathQ := getPath(root, q)
    for i := 0; i < len(pathP) && i < len(pathQ) && pathP[i] == pathQ[i]; i++ {
        ancestor = pathP[i]
    }
    return
}
[sol1-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
struct TreeNode** getPath(struct TreeNode* root, struct TreeNode* target, int* num) {
    struct TreeNode** path = malloc(sizeof(struct TreeNode*) * 2001);
    struct TreeNode* node = root;
    while (node != target) {
        path[(*num)++] = node;
        if (target->val < node->val) {
            node = node->left;
        } else {
            node = node->right;
        }
    }
    path[(*num)++] = node;
    return path;
}

struct TreeNode* lowestCommonAncestor(struct TreeNode* root, struct TreeNode* p, struct TreeNode* q) {
    int num_p = 0, num_q = 0;
    struct TreeNode** path_p = getPath(root, p, &num_p);
    struct TreeNode** path_q = getPath(root, q, &num_q);
    struct TreeNode* ancestor;
    for (int i = 0; i < num_p && i < num_q; ++i) {
        if (path_p[i] == path_q[i]) {
            ancestor = path_p[i];
        } else {
            break;
        }
    }
    return ancestor;
}

复杂度分析

  • 时间复杂度：$O(n)$，其中 $n$ 是给定的二叉搜索树中的节点个数。上述代码需要的时间与节点 $p$ 和 $q$ 在树中的深度线性相关，而在最坏的情况下，树呈现链式结构，$p$ 和 $q$ 一个是树的唯一叶子结点，一个是该叶子结点的父节点，此时时间复杂度为 $\Theta(n)$。

  • 空间复杂度：$O(n)$，我们需要存储根节点到 $p$ 和 $q$ 的路径。和上面的分析方法相同，在最坏的情况下，路径的长度为 $\Theta(n)$，因此需要 $\Theta(n)$ 的空间。

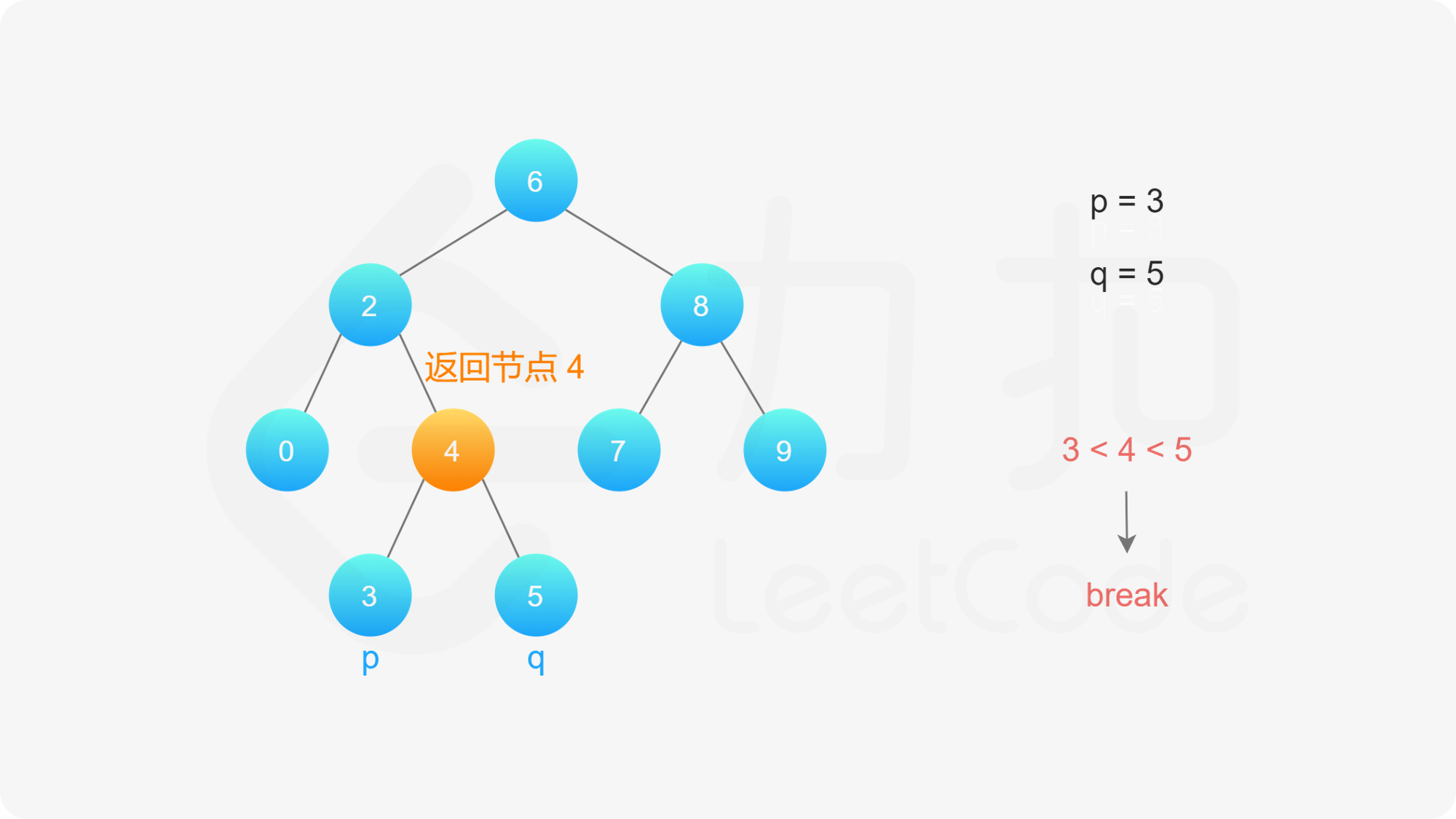
方法二：一次遍历

思路与算法

在方法一中，我们对从根节点开始，通过遍历找出到达节点 $p$ 和 $q$ 的路径，一共需要两次遍历。我们也可以考虑将这两个节点放在一起遍历。

整体的遍历过程与方法一中的类似：

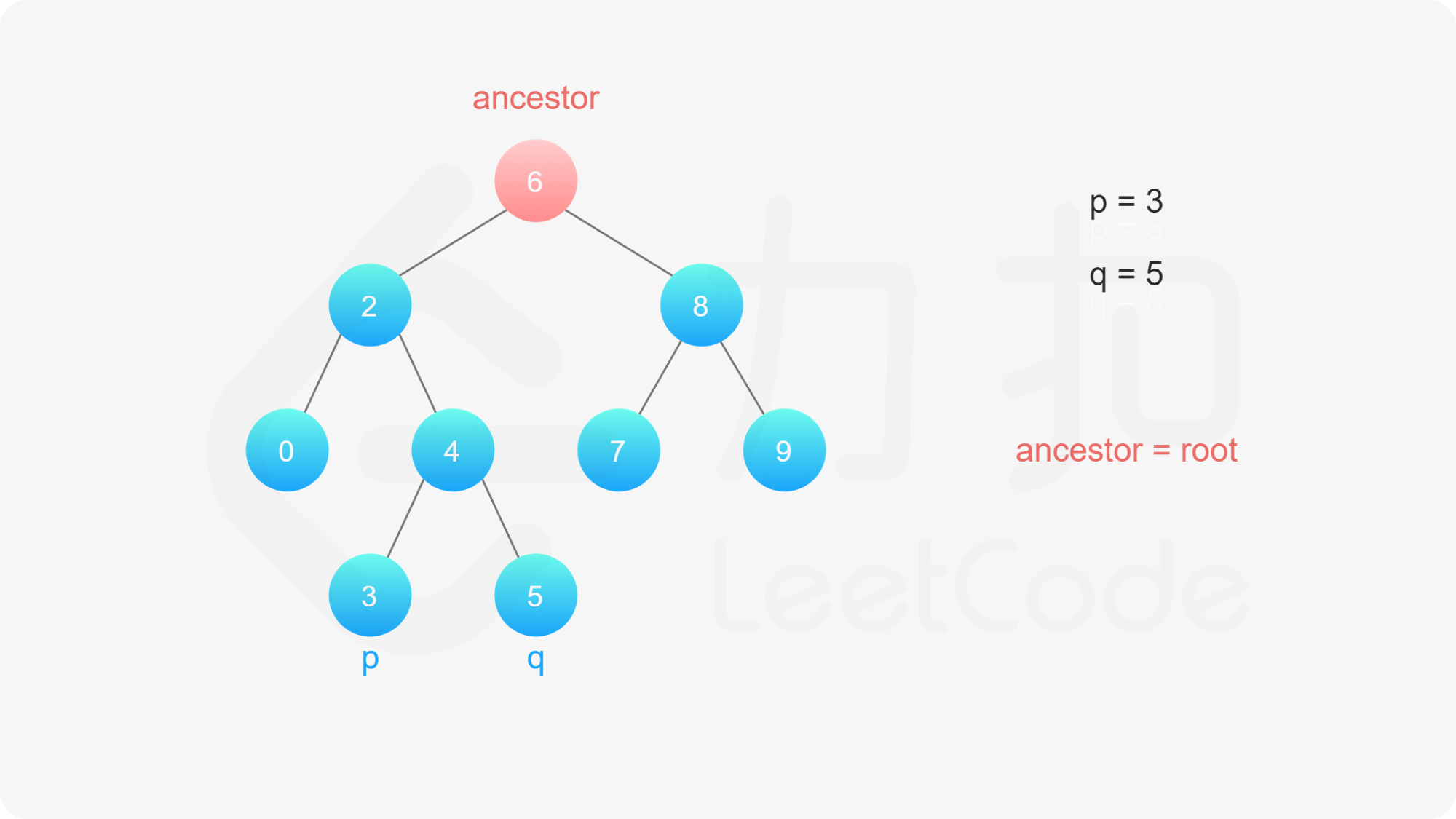
  • 我们从根节点开始遍历；

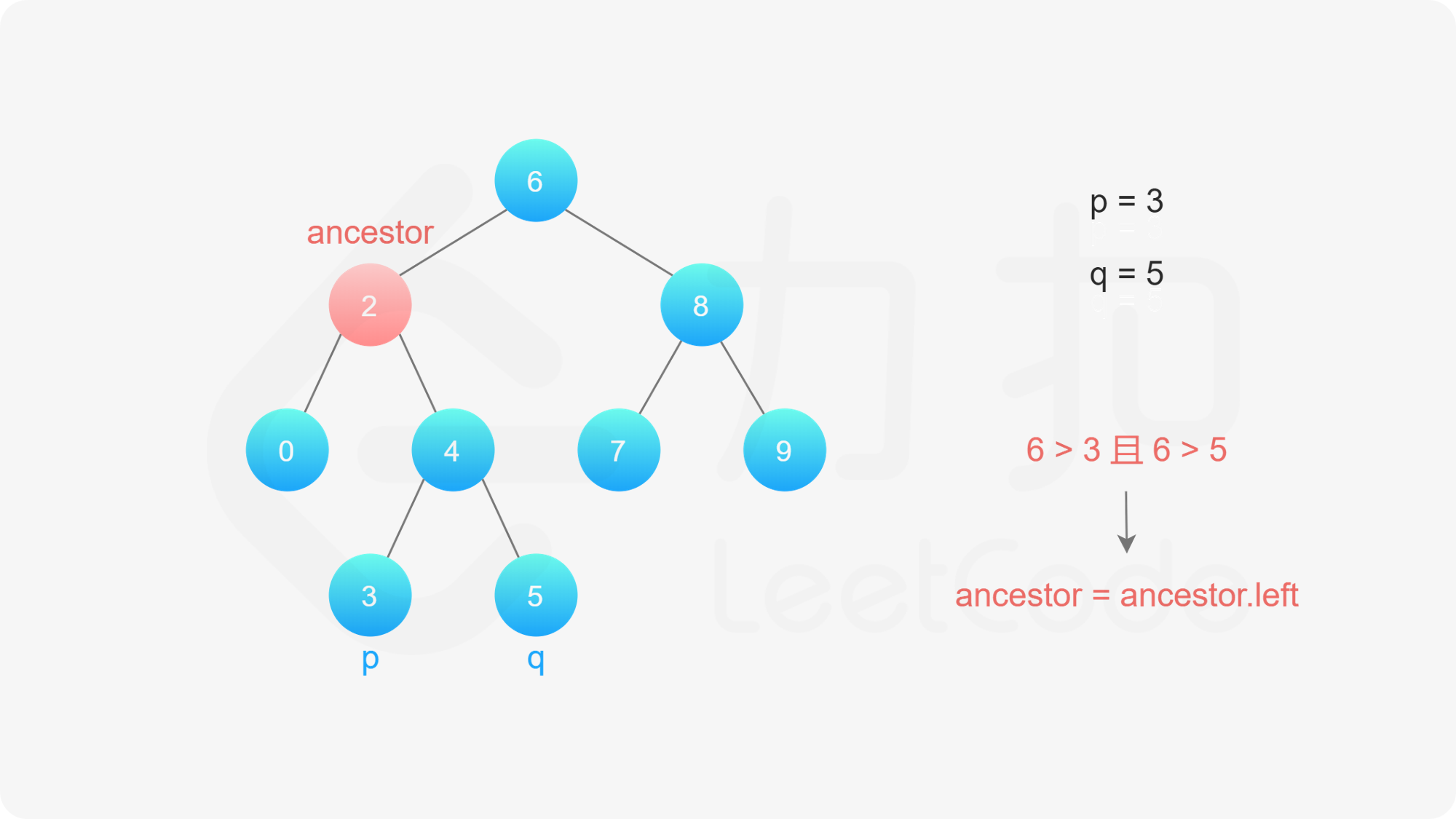
  • 如果当前节点的值大于 $p$ 和 $q$ 的值，说明 $p$ 和 $q$ 应该在当前节点的左子树，因此将当前节点移动到它的左子节点；

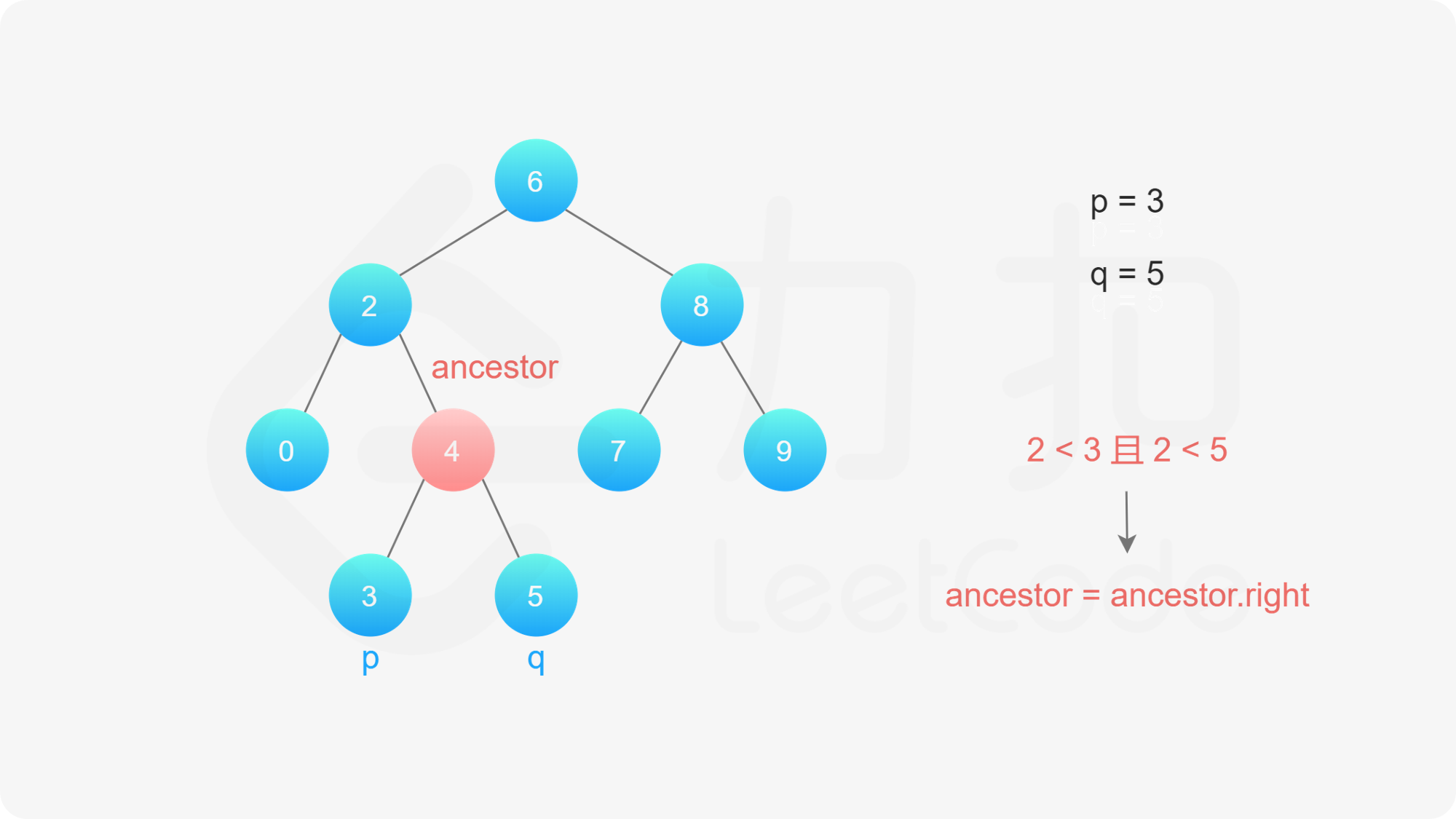
  • 如果当前节点的值小于 $p$ 和 $q$ 的值，说明 $p$ 和 $q$ 应该在当前节点的右子树，因此将当前节点移动到它的右子节点；

  • 如果当前节点的值不满足上述两条要求，那么说明当前节点就是「分岔点」。此时，$p$ 和 $q$ 要么在当前节点的不同的子树中，要么其中一个就是当前节点。

可以发现，如果我们将这两个节点放在一起遍历，我们就省去了存储路径需要的空间。

<ppt1,ppt2,ppt3,ppt4,ppt5>

代码

[sol2-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        TreeNode* ancestor = root;
        while (true) {
            if (p->val < ancestor->val && q->val < ancestor->val) {
                ancestor = ancestor->left;
            }
            else if (p->val > ancestor->val && q->val > ancestor->val) {
                ancestor = ancestor->right;
            }
            else {
                break;
            }
        }
        return ancestor;
    }
};
[sol2-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        TreeNode ancestor = root;
        while (true) {
            if (p.val < ancestor.val && q.val < ancestor.val) {
                ancestor = ancestor.left;
            } else if (p.val > ancestor.val && q.val > ancestor.val) {
                ancestor = ancestor.right;
            } else {
                break;
            }
        }
        return ancestor;
    }
}
[sol2-Python3]
1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def lowestCommonAncestor(self, root: TreeNode, p: TreeNode, q: TreeNode) -> TreeNode:
        ancestor = root
        while True:
            if p.val < ancestor.val and q.val < ancestor.val:
                ancestor = ancestor.left
            elif p.val > ancestor.val and q.val > ancestor.val:
                ancestor = ancestor.right
            else:
                break
        return ancestor
[sol2-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
func lowestCommonAncestor(root, p, q *TreeNode) (ancestor *TreeNode) {
    ancestor = root
    for {
        if p.Val < ancestor.Val && q.Val < ancestor.Val {
            ancestor = ancestor.Left
        } else if p.Val > ancestor.Val && q.Val > ancestor.Val {
            ancestor = ancestor.Right
        } else {
            return
        }
    }
}
[sol2-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
struct TreeNode* lowestCommonAncestor(struct TreeNode* root, struct TreeNode* p, struct TreeNode* q) {
    struct TreeNode* ancestor = root;
    while (true) {
        if (p->val < ancestor->val && q->val < ancestor->val) {
            ancestor = ancestor->left;
        } else if (p->val > ancestor->val && q->val > ancestor->val) {
            ancestor = ancestor->right;
        } else {
            break;
        }
    }
    return ancestor;
}

复杂度分析

  • 时间复杂度：$O(n)$，其中 $n$ 是给定的二叉搜索树中的节点个数。分析思路与方法一相同。

  • 空间复杂度：$O(1)$。

 Comments
On this page
0235-二叉搜索树的最近公共祖先