给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 不要使用除法, 且在 O( _n_ ) 时间复杂度内完成此题。
示例 1:
**输入:** nums = [1,2,3,4]
**输出:** [24,12,8,6]
示例 2:
**输入:** nums = [-1,1,0,-3,3]
**输出:** [0,0,9,0,0]
提示:
2 <= nums.length <= 105-30 <= nums[i] <= 30保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内
进阶: 你可以在 O(1) 的额外空间复杂度内完成这个题目吗?( 出于对空间复杂度分析的目的,输出数组 不被视为 额外空间。)
📺视频题解
📖文字题解 前言 这似乎是一个简单的问题,可以在线性时间和空间内解决。先计算给定数组所有元素的乘积,然后对数组中的每个元素 $x$,将总的乘积除以 $x$ 来求得除自身值的以外数组的乘积。
然而这样的解决方法有一个问题,就是如果输入数组中出现 0,那么这个方法就失效了。而且在问题中说明了不允许使用除法运算。这增加了这个问题的难度。
方法一:左右乘积列表 思路
我们不必将所有数字的乘积除以给定索引处的数字得到相应的答案,而是利用索引左侧所有数字的乘积和右侧所有数字的乘积(即前缀与后缀)相乘得到答案。
对于给定索引 $i$,我们将使用它左边所有数字的乘积乘以右边所有数字的乘积。下面让我们更加具体的描述这个算法。
算法
初始化两个空数组 L 和 R。对于给定索引 i,L[i] 代表的是 i 左侧所有数字的乘积,R[i] 代表的是 i 右侧所有数字的乘积。
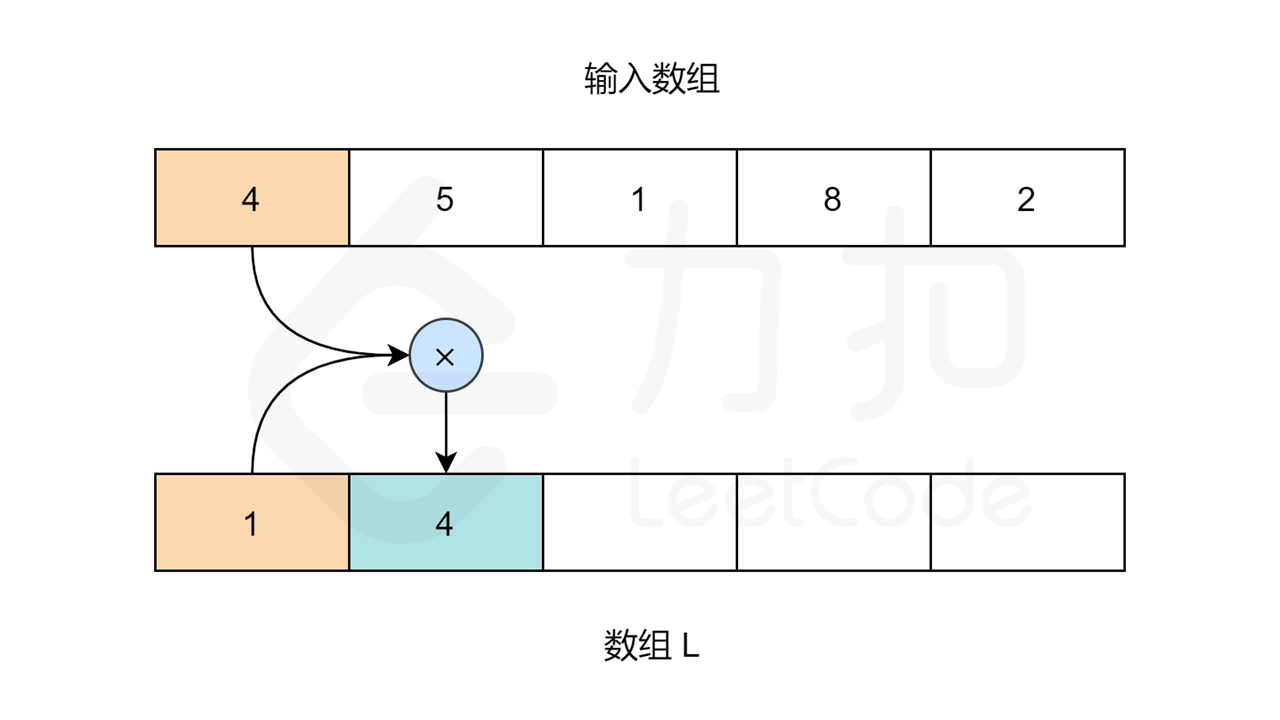
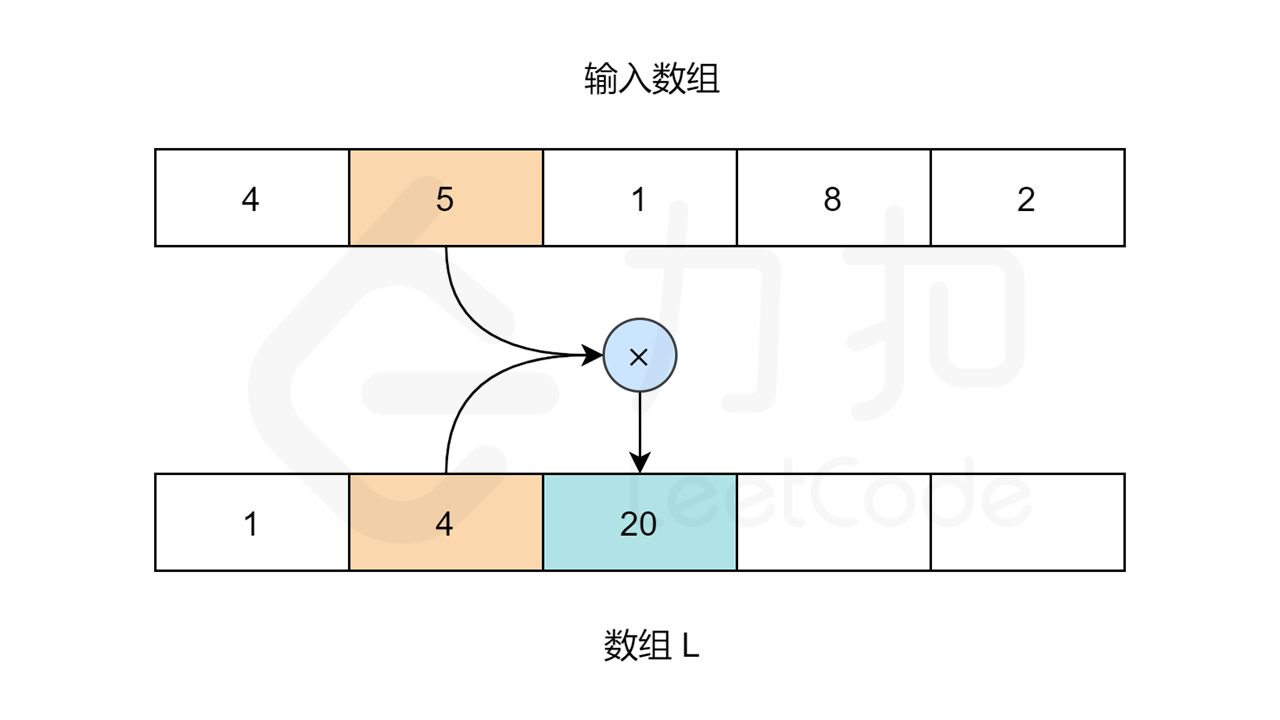
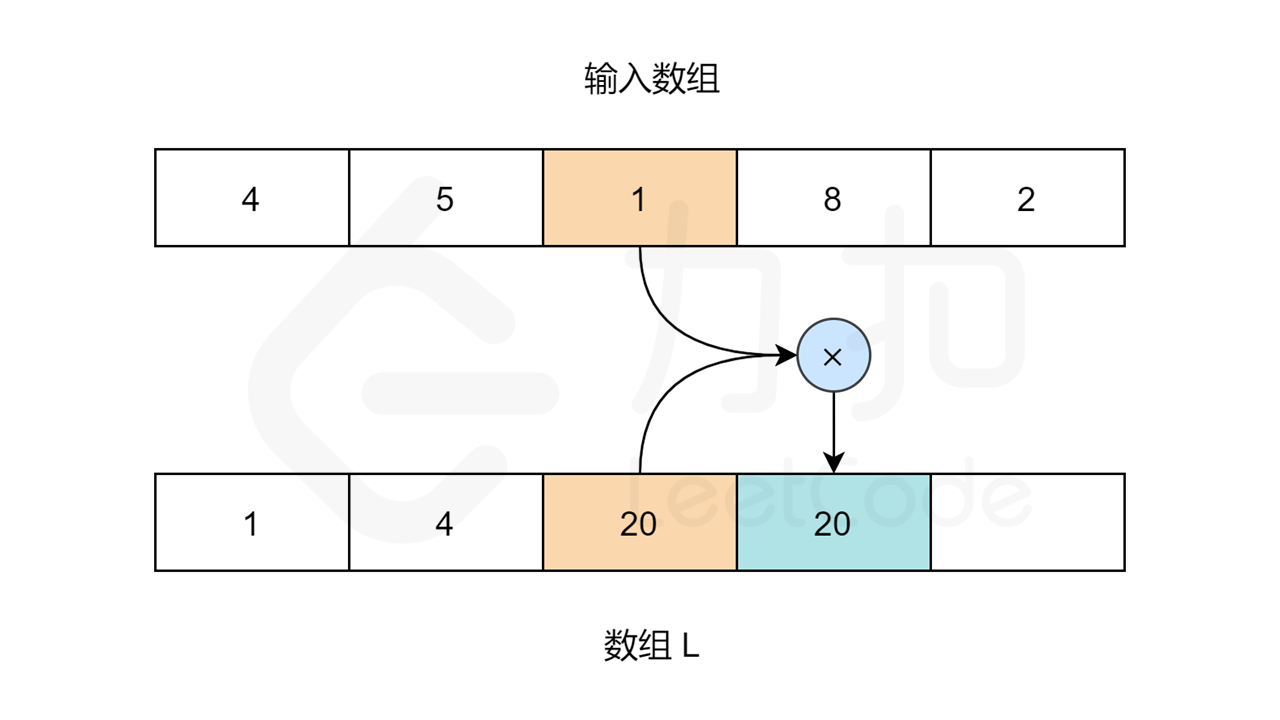
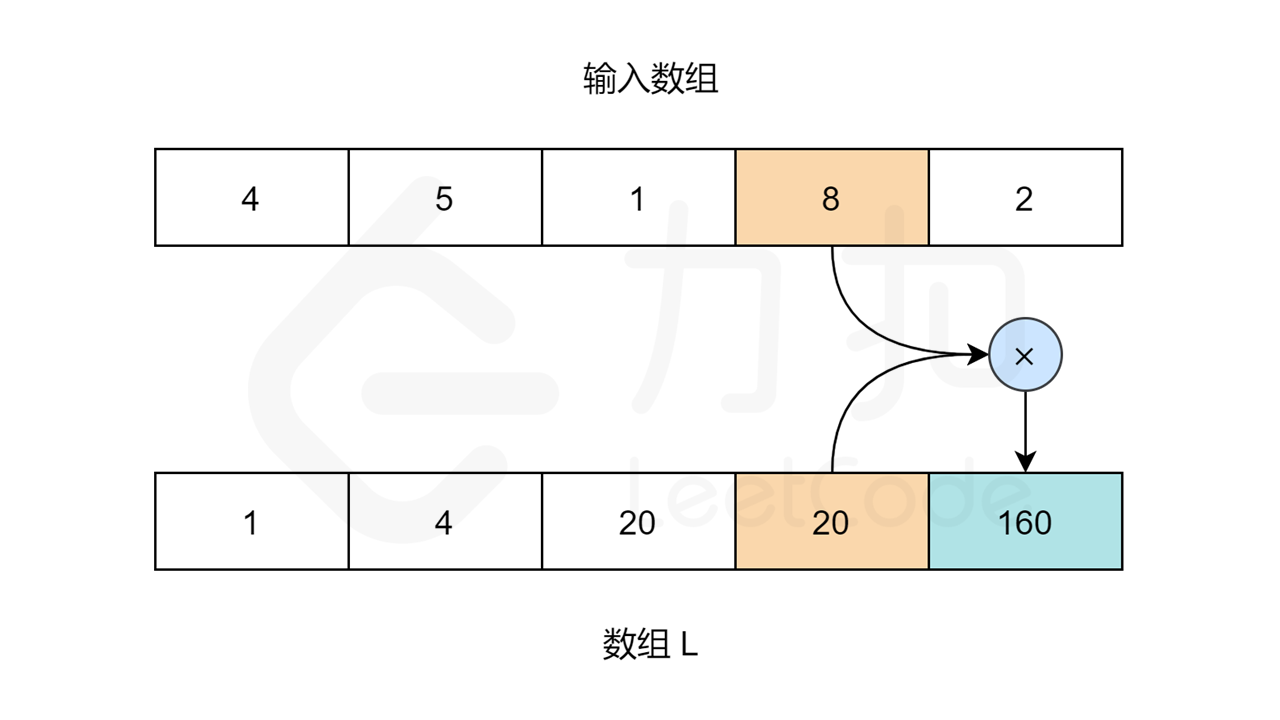
我们需要用两个循环来填充 L 和 R 数组的值。对于数组 L,L[0] 应该是 1,因为第一个元素的左边没有元素。对于其他元素:L[i] = L[i-1] * nums[i-1]。
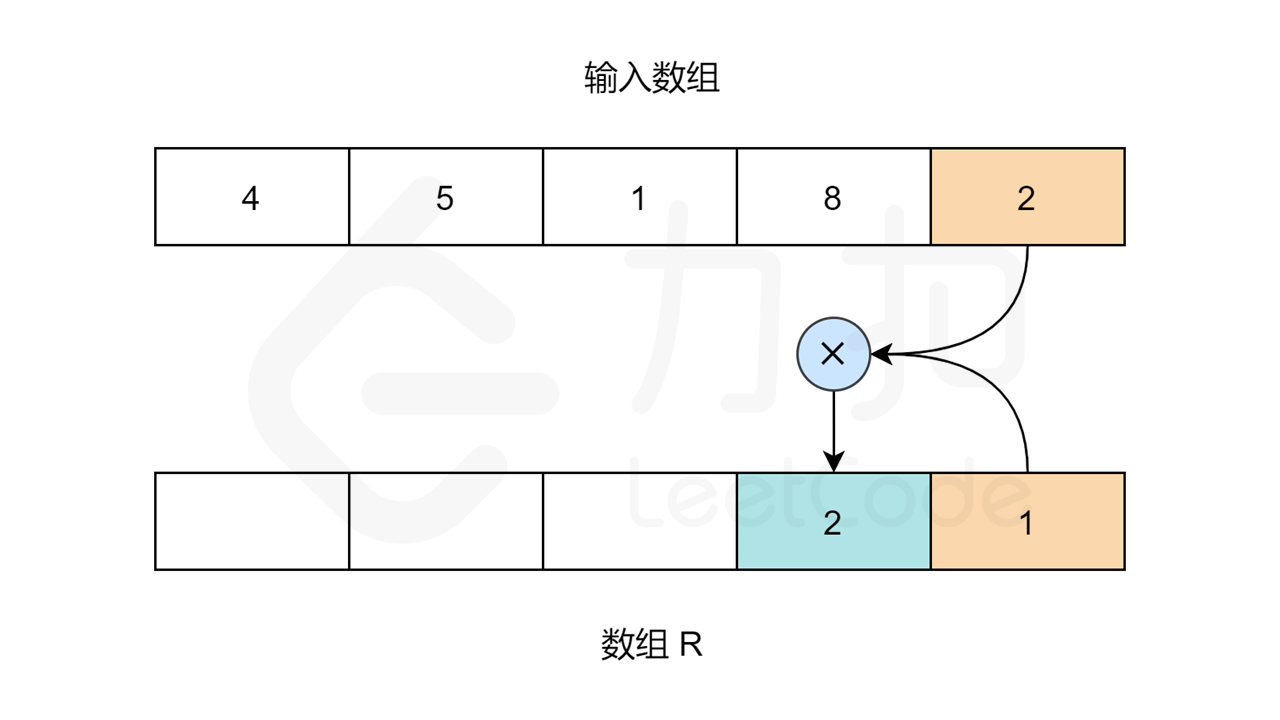
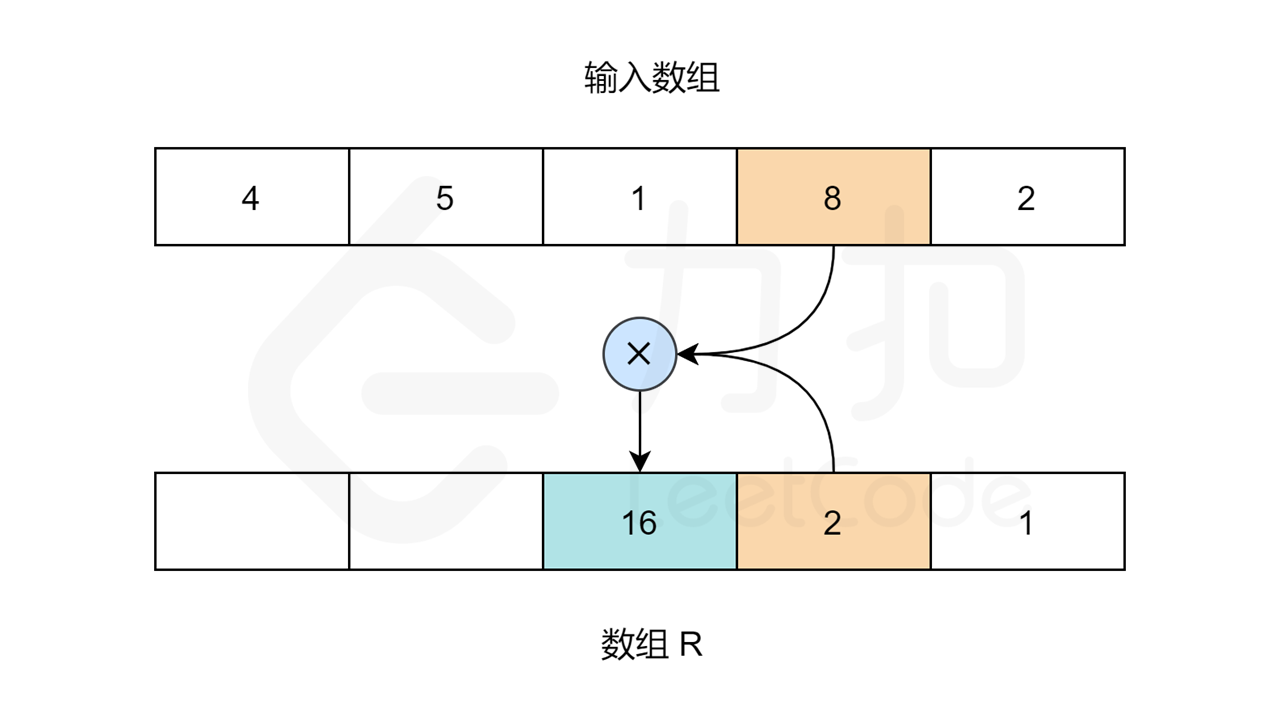
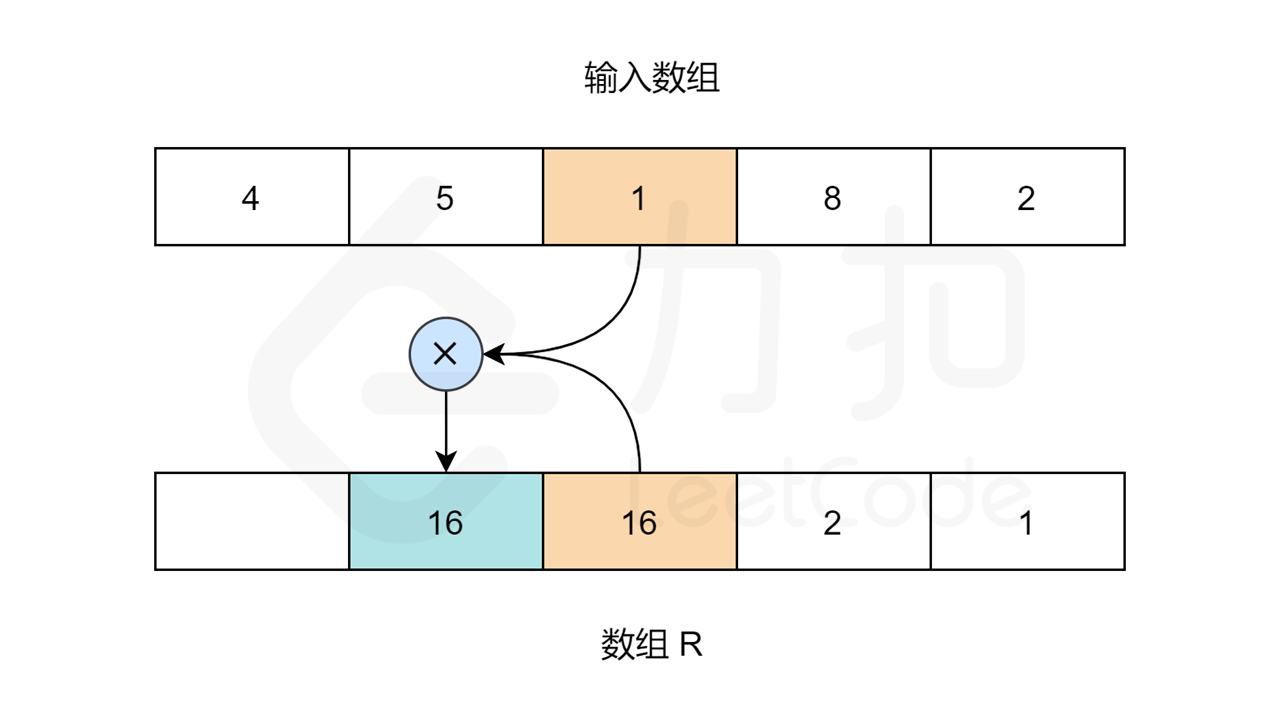
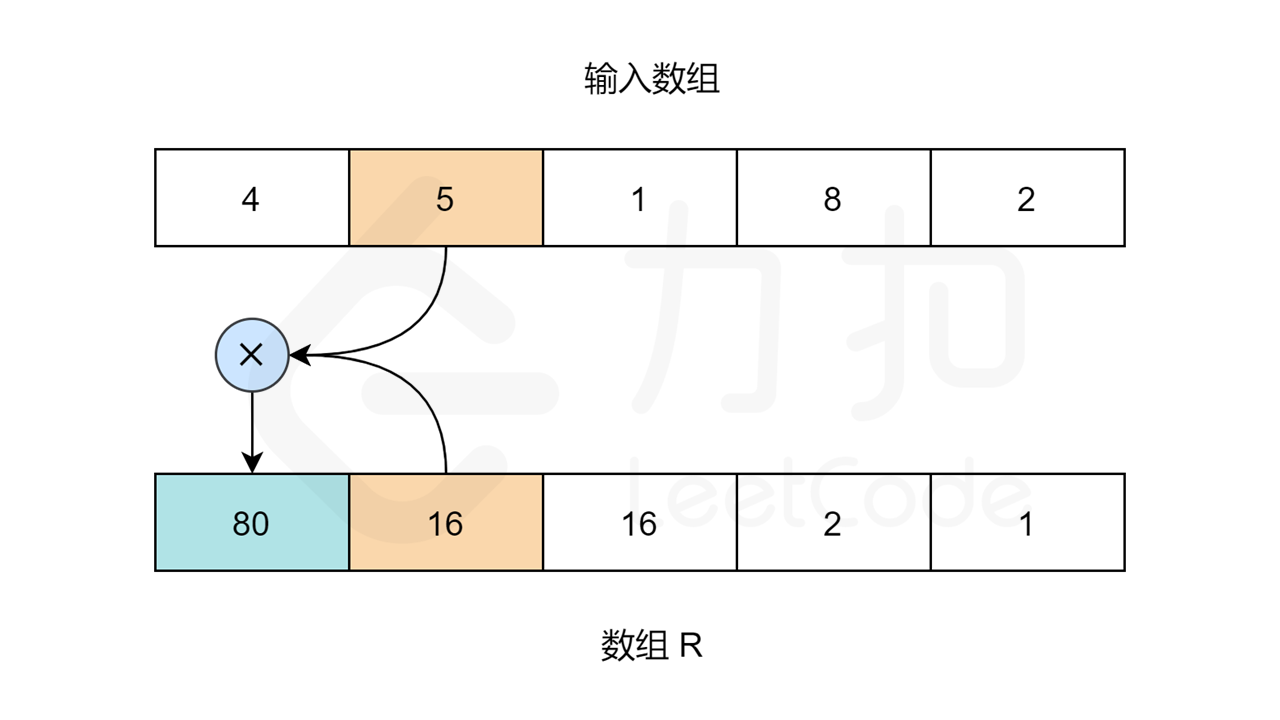
同理,对于数组 R,R[length-1] 应为 1。length 指的是输入数组的大小。其他元素:R[i] = R[i+1] * nums[i+1]。
当 R 和 L 数组填充完成,我们只需要在输入数组上迭代,且索引 i 处的值为:L[i] * R[i]。
让我们用以下图片看看算法是如何工作的:
<
[sol1-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 class Solution {public : vector<int > productExceptSelf (vector<int >& nums) { int length = nums.size (); vector<int > L (length, 0 ) , R (length, 0 ) ; vector<int > answer (length) ; L[0 ] = 1 ; for (int i = 1 ; i < length; i++) { L[i] = nums[i - 1 ] * L[i - 1 ]; } R[length - 1 ] = 1 ; for (int i = length - 2 ; i >= 0 ; i--) { R[i] = nums[i + 1 ] * R[i + 1 ]; } for (int i = 0 ; i < length; i++) { answer[i] = L[i] * R[i]; } return answer; } };
[sol1-Python3] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution : def productExceptSelf (self, nums: List [int ] ) -> List [int ]: length = len (nums) L, R, answer = [0 ]*length, [0 ]*length, [0 ]*length L[0 ] = 1 for i in range (1 , length): L[i] = nums[i - 1 ] * L[i - 1 ] R[length - 1 ] = 1 for i in reversed (range (length - 1 )): R[i] = nums[i + 1 ] * R[i + 1 ] for i in range (length): answer[i] = L[i] * R[i] return answer
[sol1-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 class Solution { public int [] productExceptSelf(int [] nums) { int length = nums.length; int [] L = new int [length]; int [] R = new int [length]; int [] answer = new int [length]; L[0 ] = 1 ; for (int i = 1 ; i < length; i++) { L[i] = nums[i - 1 ] * L[i - 1 ]; } R[length - 1 ] = 1 ; for (int i = length - 2 ; i >= 0 ; i--) { R[i] = nums[i + 1 ] * R[i + 1 ]; } for (int i = 0 ; i < length; i++) { answer[i] = L[i] * R[i]; } return answer; } }
[sol1-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 func productExceptSelf (nums []int ) int { length := len (nums) L, R, answer := make ([]int , length), make ([]int , length), make ([]int , length) L[0 ] = 1 for i := 1 ; i < length; i++ { L[i] = nums[i-1 ] * L[i-1 ] } R[length-1 ] = 1 for i := length - 2 ; i >= 0 ; i-- { R[i] = nums[i+1 ] * R[i+1 ] } for i := 0 ; i < length; i++ { answer[i] = L[i] * R[i] } return answer }
[sol1-TypeScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 var productExceptSelf = function (nums: number [] ): number [] { const length = nums.length ; const L = new Array <number >(length); const R = new Array <number >(length); const answer = new Array <number >(length); L[0 ] = 1 ; for (let i = 1 ; i < length; i++) { L[i] = nums[i - 1 ] * L[i - 1 ]; } R[length - 1 ] = 1 ; for (let i = length - 2 ; i >= 0 ; i--) { R[i] = nums[i + 1 ] * R[i + 1 ]; } for (let i = 0 ; i < length; i++) { answer[i] = L[i] * R[i]; } return answer; };
复杂度分析
时间复杂度:$O(N)$,其中 $N$ 指的是数组 nums 的大小。预处理 L 和 R 数组以及最后的遍历计算都是 $O(N)$ 的时间复杂度。
空间复杂度:$O(N)$,其中 $N$ 指的是数组 nums 的大小。使用了 L 和 R 数组去构造答案,L 和 R 数组的长度为数组 nums 的大小。
方法二:空间复杂度 $O(1)$ 的方法 思路
尽管上面的方法已经能够很好的解决这个问题,但是空间复杂度并不为常数。
由于输出数组不算在空间复杂度内,那么我们可以将 L 或 R 数组用输出数组来计算。先把输出数组当作 L 数组来计算,然后再动态构造 R 数组得到结果。让我们来看看基于这个思想的算法。
算法
初始化 answer 数组,对于给定索引 i,answer[i] 代表的是 i 左侧所有数字的乘积。
构造方式与之前相同,只是我们试图节省空间,先把 answer 作为方法一的 L 数组。
这种方法的唯一变化就是我们没有构造 R 数组。而是用一个遍历来跟踪右边元素的乘积。并更新数组 $answer[i]=answer[i]R$。然后 $R$ 更新为 $R=R nums[i]$,其中变量 $R$ 表示的就是索引右侧数字的乘积。
[sol2-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution {public : vector<int > productExceptSelf (vector<int >& nums) { int length = nums.size (); vector<int > answer (length) ; answer[0 ] = 1 ; for (int i = 1 ; i < length; i++) { answer[i] = nums[i - 1 ] * answer[i - 1 ]; } int R = 1 ; for (int i = length - 1 ; i >= 0 ; i--) { answer[i] = answer[i] * R; R *= nums[i]; } return answer; } };
[sol2-Python3] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution : def productExceptSelf (self, nums: List [int ] ) -> List [int ]: length = len (nums) answer = [0 ]*length answer[0 ] = 1 for i in range (1 , length): answer[i] = nums[i - 1 ] * answer[i - 1 ] R = 1 ; for i in reversed (range (length)): answer[i] = answer[i] * R R *= nums[i] return answer
[sol2-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution { public int [] productExceptSelf(int [] nums) { int length = nums.length; int [] answer = new int [length]; answer[0 ] = 1 ; for (int i = 1 ; i < length; i++) { answer[i] = nums[i - 1 ] * answer[i - 1 ]; } int R = 1 ; for (int i = length - 1 ; i >= 0 ; i--) { answer[i] = answer[i] * R; R *= nums[i]; } return answer; } }
[sol2-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 func productExceptSelf (nums []int ) int { length := len (nums) answer := make ([]int , length) answer[0 ] = 1 for i := 1 ; i < length; i++ { answer[i] = nums[i-1 ] * answer[i-1 ] } R := 1 for i := length - 1 ; i >= 0 ; i-- { answer[i] = answer[i] * R R *= nums[i] } return answer }
[sol2-TypeScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 var productExceptSelf = function (nums: number [] ): number [] { const length = nums.length ; const answer = new Array <number >(length); answer[0 ] = 1 ; for (let i = 1 ; i < length; i++) { answer[i] = nums[i - 1 ] * answer[i - 1 ]; } let R = 1 ; for (let i = length - 1 ; i >= 0 ; i--) { answer[i] = answer[i] * R; R *= nums[i]; } return answer; };
复杂度分析
时间复杂度:$O(N)$,其中 $N$ 指的是数组 nums 的大小。分析与方法一相同。
空间复杂度:$O(1)$,输出数组不算进空间复杂度中,因此我们只需要常数的空间存放变量。