给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
示例 1:

**输入:** root = [1,2,3,null,5]
**输出:** ["1->2->5","1->3"]
示例 2:
**输入:** root = [1]
**输出:** ["1"]
提示:
- 树中节点的数目在范围
[1, 100] 内
-100 <= Node.val <= 100
方法一:深度优先搜索
思路与算法
最直观的方法是使用深度优先搜索。在深度优先搜索遍历二叉树时,我们需要考虑当前的节点以及它的孩子节点。
- 如果当前节点不是叶子节点,则在当前的路径末尾添加该节点,并继续递归遍历该节点的每一个孩子节点。
- 如果当前节点是叶子节点,则在当前路径末尾添加该节点后我们就得到了一条从根节点到叶子节点的路径,将该路径加入到答案即可。
如此,当遍历完整棵二叉树以后我们就得到了所有从根节点到叶子节点的路径。当然,深度优先搜索也可以使用非递归的方式实现,这里不再赘述。
代码
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public:
void construct_paths(TreeNode* root, string path, vector<string>& paths) {
if (root != nullptr) {
path += to_string(root->val);
if (root->left == nullptr && root->right == nullptr) {
paths.push_back(path);
} else {
path += "->";
construct_paths(root->left, path, paths);
construct_paths(root->right, path, paths);
}
}
}
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> paths;
construct_paths(root, "", paths);
return paths;
}
};
|
[sol1-JavaScript]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| var binaryTreePaths = function(root) {
const paths = [];
const construct_paths = (root, path) => {
if (root) {
path += root.val.toString();
if (root.left === null && root.right === null) {
paths.push(path);
} else {
path += "->";
construct_paths(root.left, path);
construct_paths(root.right, path);
}
}
}
construct_paths(root, "");
return paths;
};
|
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public List<String> binaryTreePaths(TreeNode root) {
List<String> paths = new ArrayList<String>();
constructPaths(root, "", paths);
return paths;
}
public void constructPaths(TreeNode root, String path, List<String> paths) {
if (root != null) {
StringBuffer pathSB = new StringBuffer(path);
pathSB.append(Integer.toString(root.val));
if (root.left == null && root.right == null) {
paths.add(pathSB.toString());
} else {
pathSB.append("->");
constructPaths(root.left, pathSB.toString(), paths);
constructPaths(root.right, pathSB.toString(), paths);
}
}
}
}
|
[sol1-Python]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution:
def binaryTreePaths(self, root):
"""
:type root: TreeNode
:rtype: List[str]
"""
def construct_paths(root, path):
if root:
path += str(root.val)
if not root.left and not root.right:
paths.append(path)
else:
path += '->'
construct_paths(root.left, path)
construct_paths(root.right, path)
paths = []
construct_paths(root, '')
return paths
|
[sol1-Golang]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| var paths []string
func binaryTreePaths(root *TreeNode) []string {
paths = []string{}
constructPaths(root, "")
return paths
}
func constructPaths(root *TreeNode, path string) {
if root != nil {
pathSB := path
pathSB += strconv.Itoa(root.Val)
if root.Left == nil && root.Right == nil {
paths = append(paths, pathSB)
} else {
pathSB += "->"
constructPaths(root.Left, pathSB)
constructPaths(root.Right, pathSB)
}
}
}
|
[sol1-C]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| void construct_paths(struct TreeNode* root, char** paths, int* returnSize, int* sta, int top) {
if (root != NULL) {
if (root->left == NULL && root->right == NULL) {
char* tmp = (char*)malloc(1001);
int len = 0;
for (int i = 0; i < top; i++) {
len += sprintf(tmp + len, "%d->", sta[i]);
}
sprintf(tmp + len, "%d", root->val);
paths[(*returnSize)++] = tmp;
} else {
sta[top++] = root->val;
construct_paths(root->left, paths, returnSize, sta, top);
construct_paths(root->right, paths, returnSize, sta, top);
}
}
}
char** binaryTreePaths(struct TreeNode* root, int* returnSize) {
char** paths = (char**)malloc(sizeof(char*) * 1001);
*returnSize = 0;
int sta[1001];
construct_paths(root, paths, returnSize, sta, 0);
return paths;
}
|
复杂度分析
时间复杂度:$O(N^2)$,其中 $N$ 表示节点数目。在深度优先搜索中每个节点会被访问一次且只会被访问一次,每一次会对 path 变量进行拷贝构造,时间代价为 $O(N)$,故时间复杂度为 $O(N^2)$。
空间复杂度:$O(N^2)$,其中 $N$ 表示节点数目。除答案数组外我们需要考虑递归调用的栈空间。在最坏情况下,当二叉树中每个节点只有一个孩子节点时,即整棵二叉树呈一个链状,此时递归的层数为 $N$,此时每一层的 path 变量的空间代价的总和为 $O(\sum_{i = 1}^{N} i) = O(N^2)$ 空间复杂度为 $O(N^2)$。最好情况下,当二叉树为平衡二叉树时,它的高度为 $\log N$,此时空间复杂度为 $O((\log {N})^2)$。
方法二:广度优先搜索
思路与算法
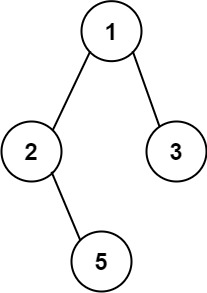
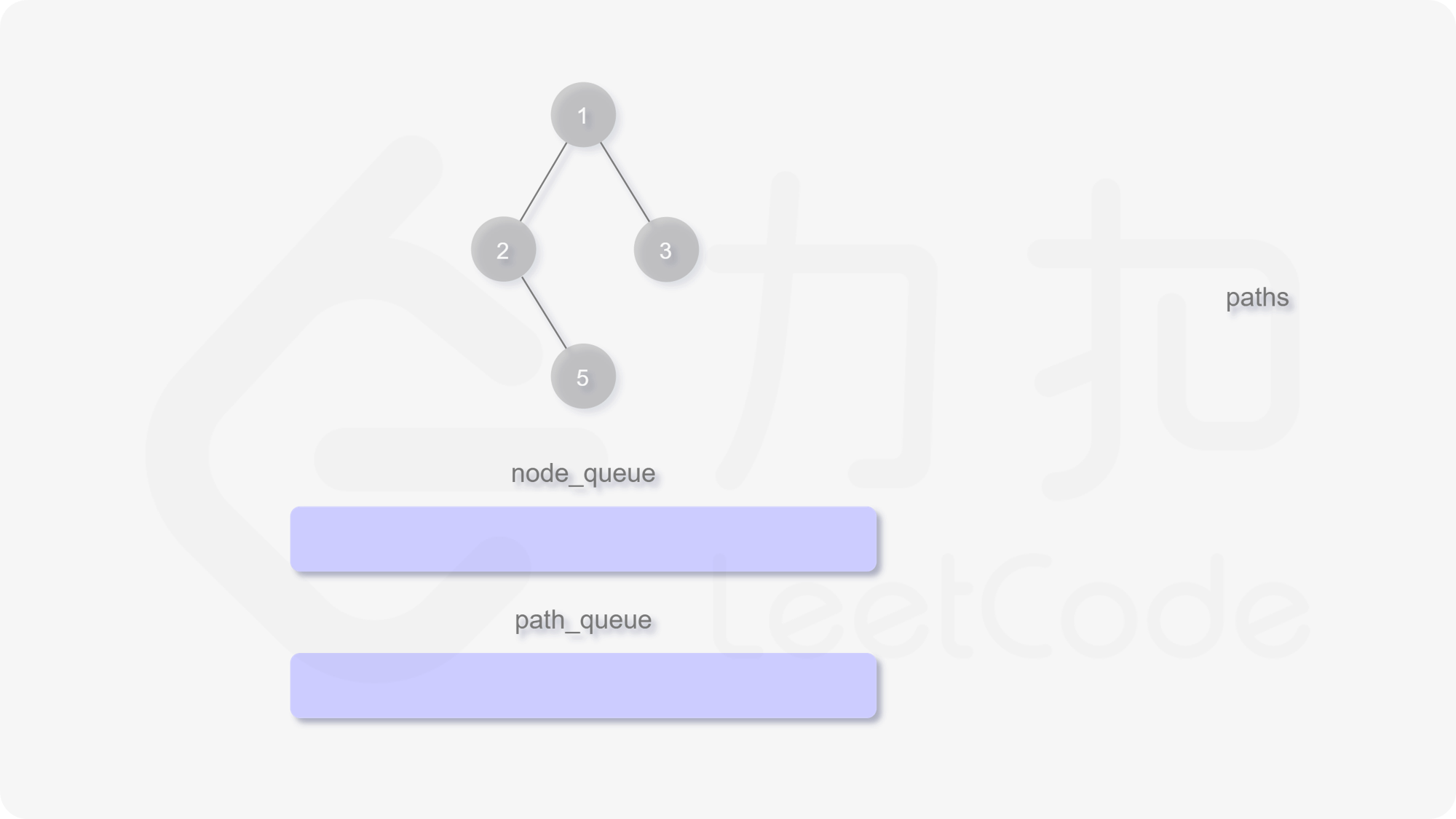
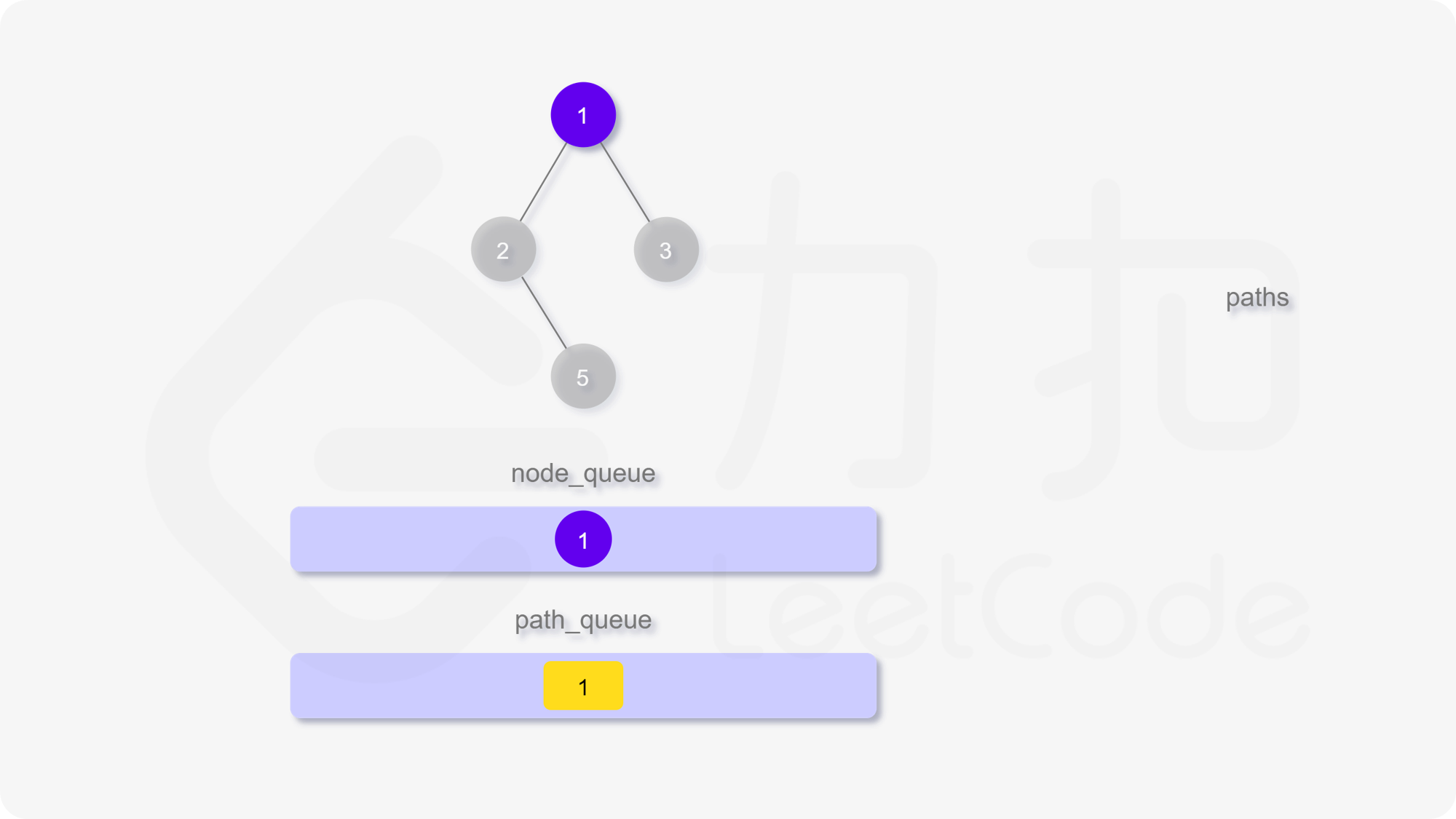
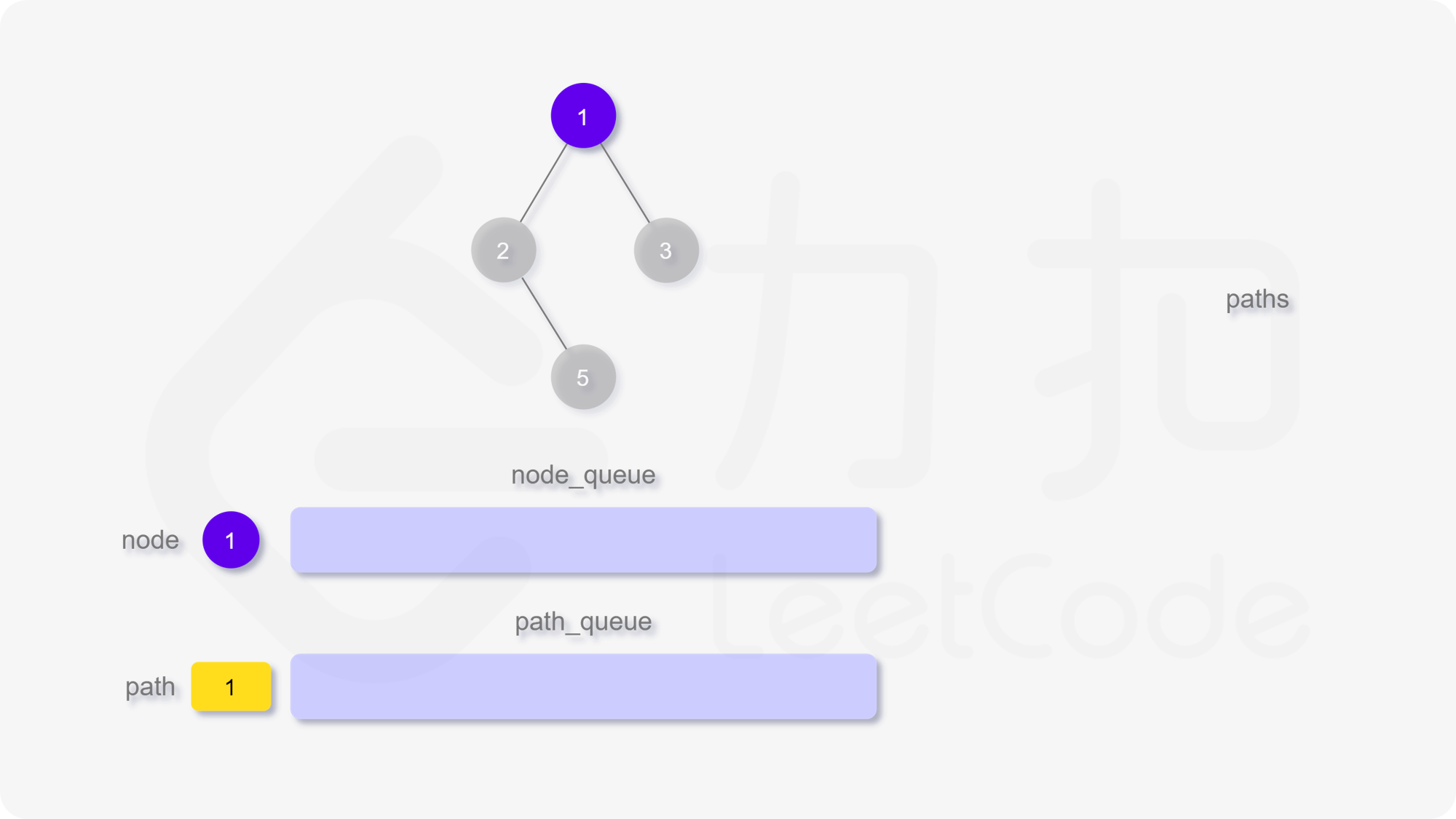
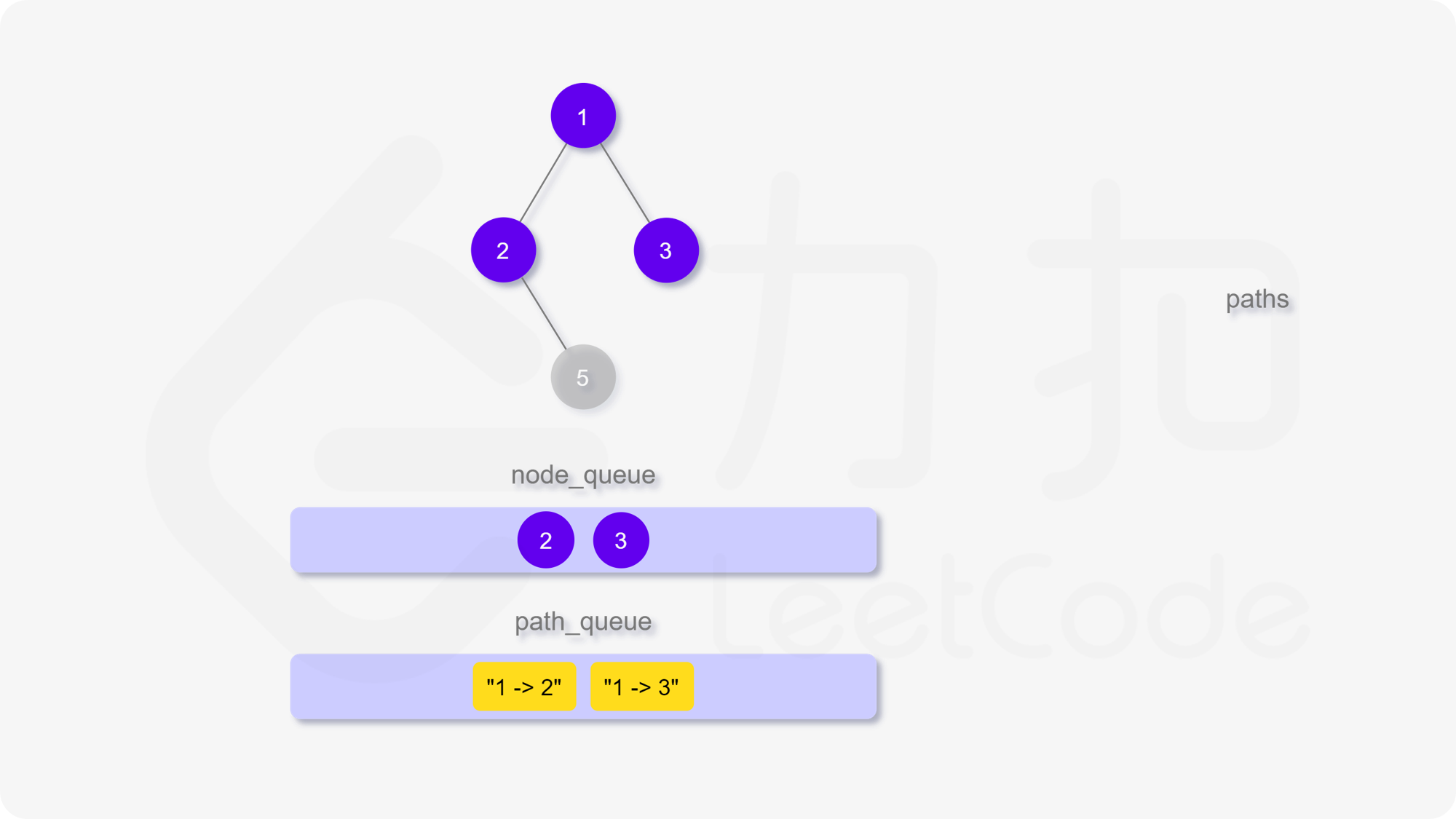
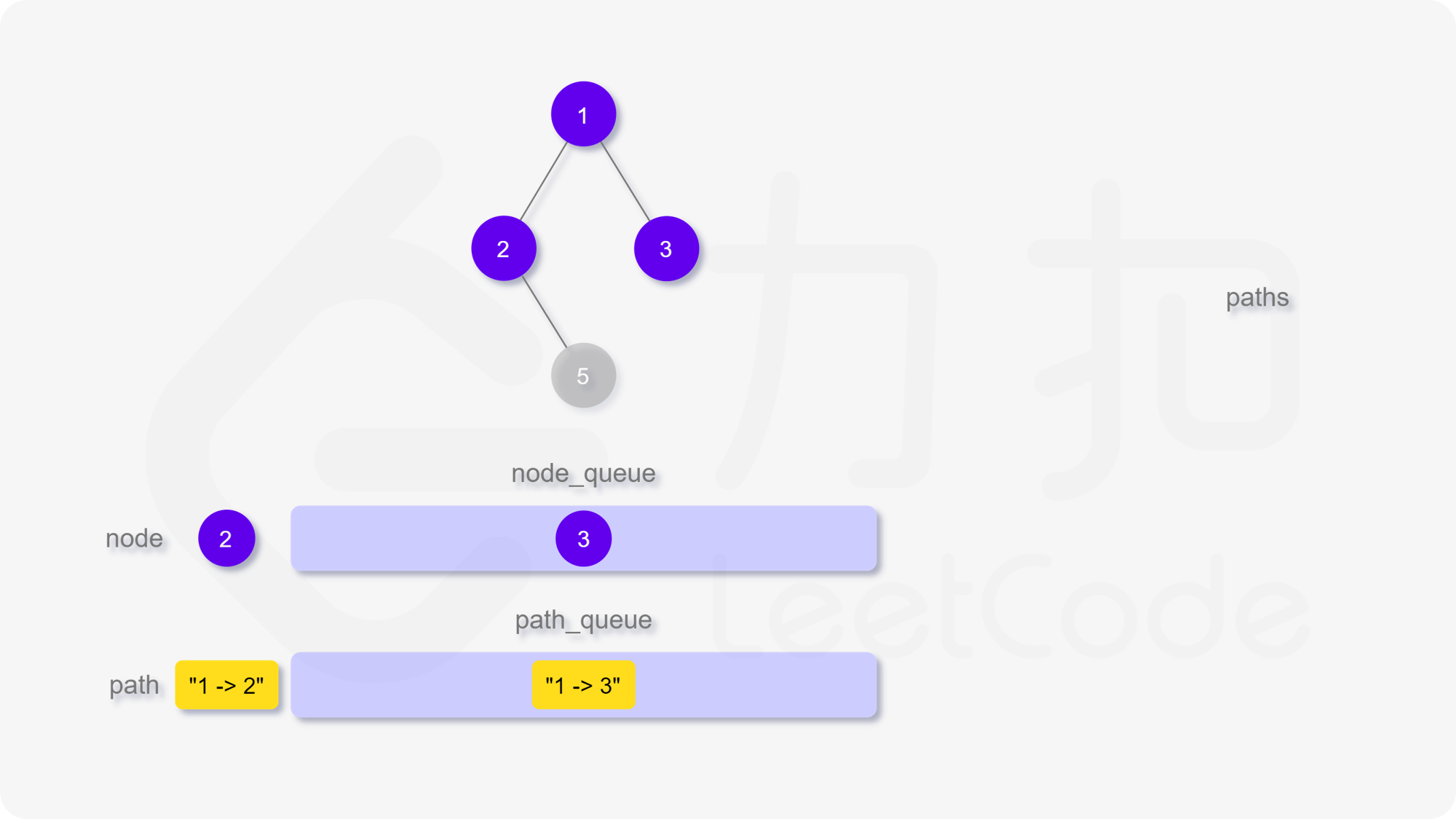
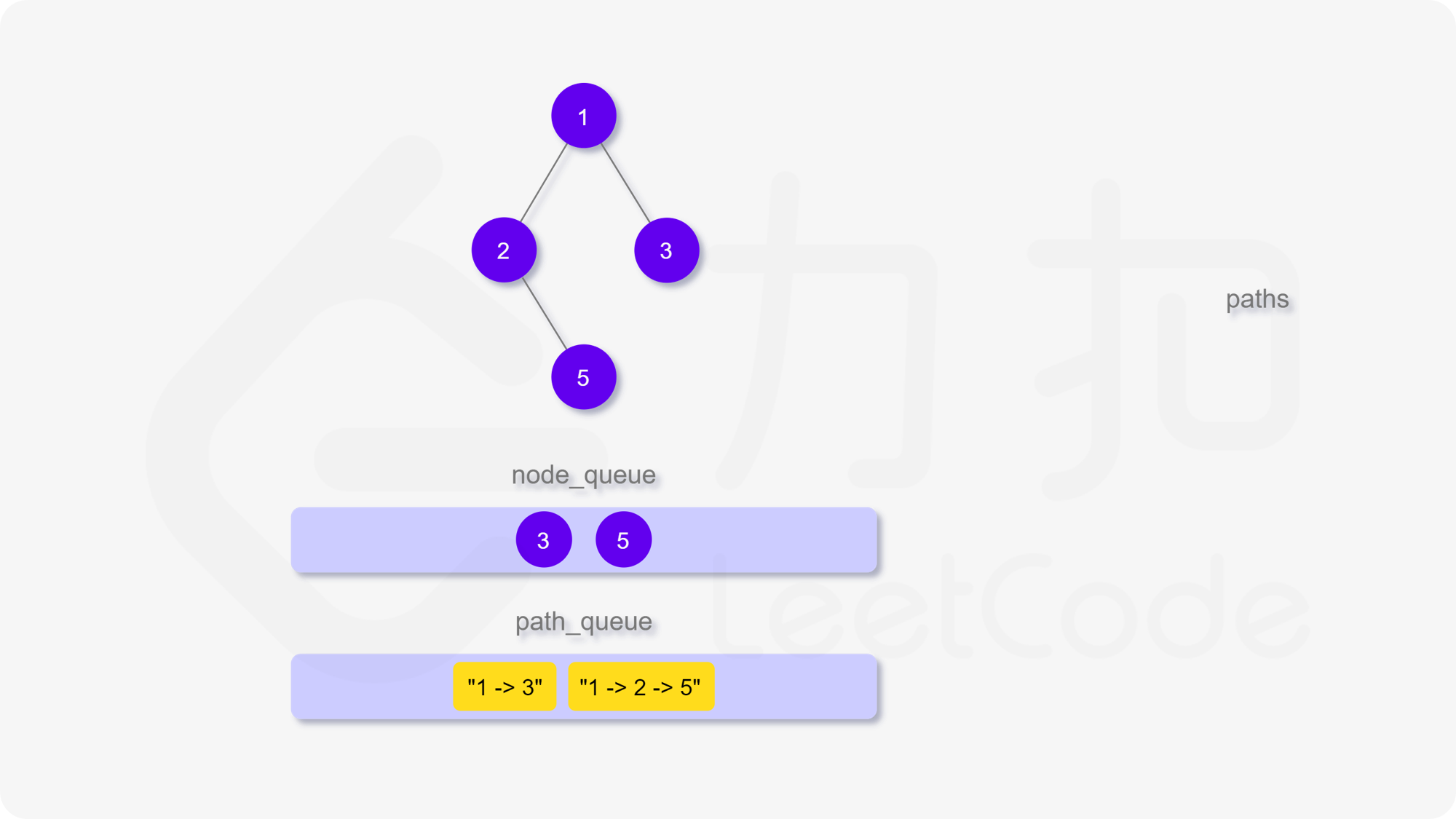
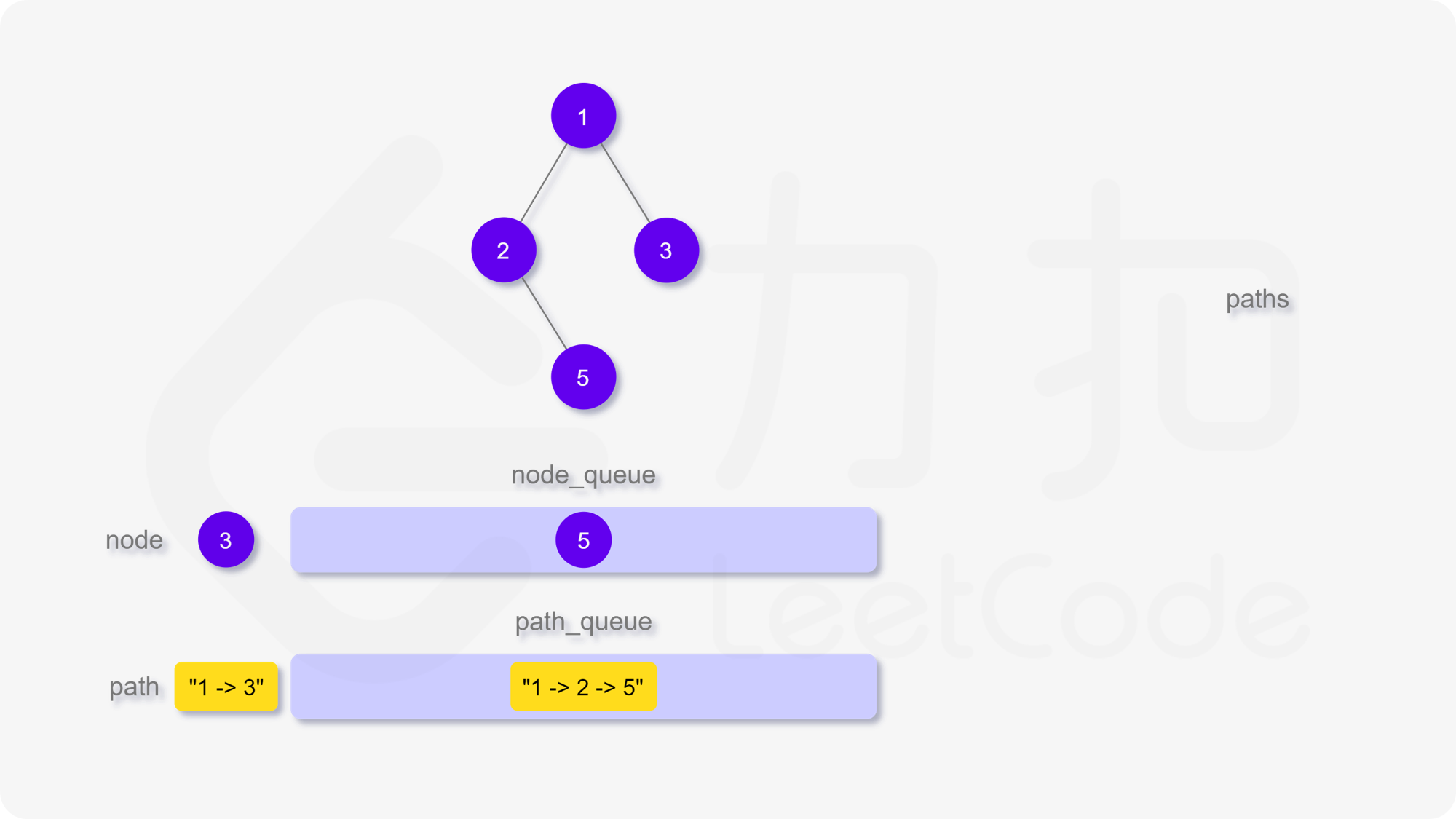
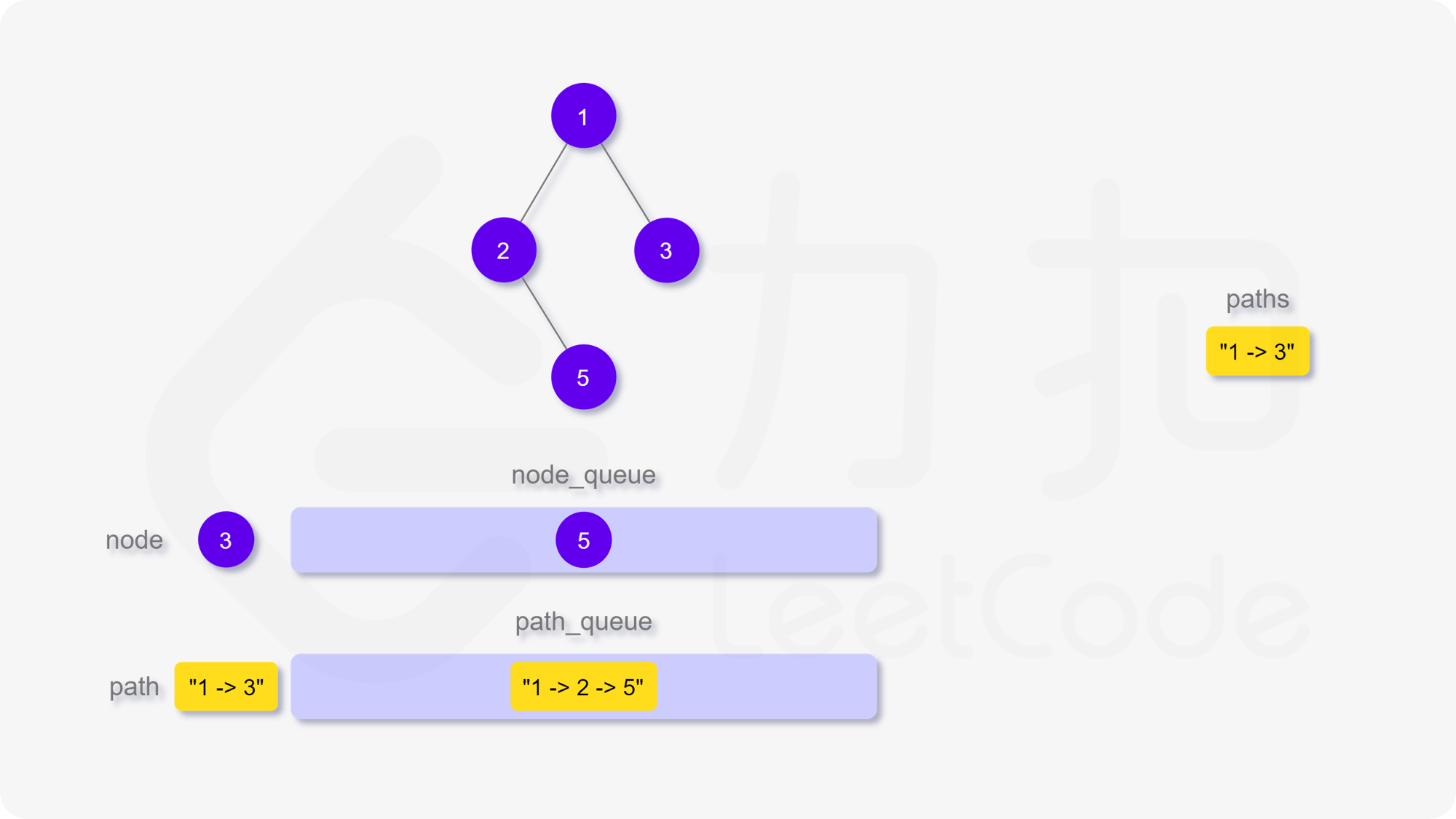
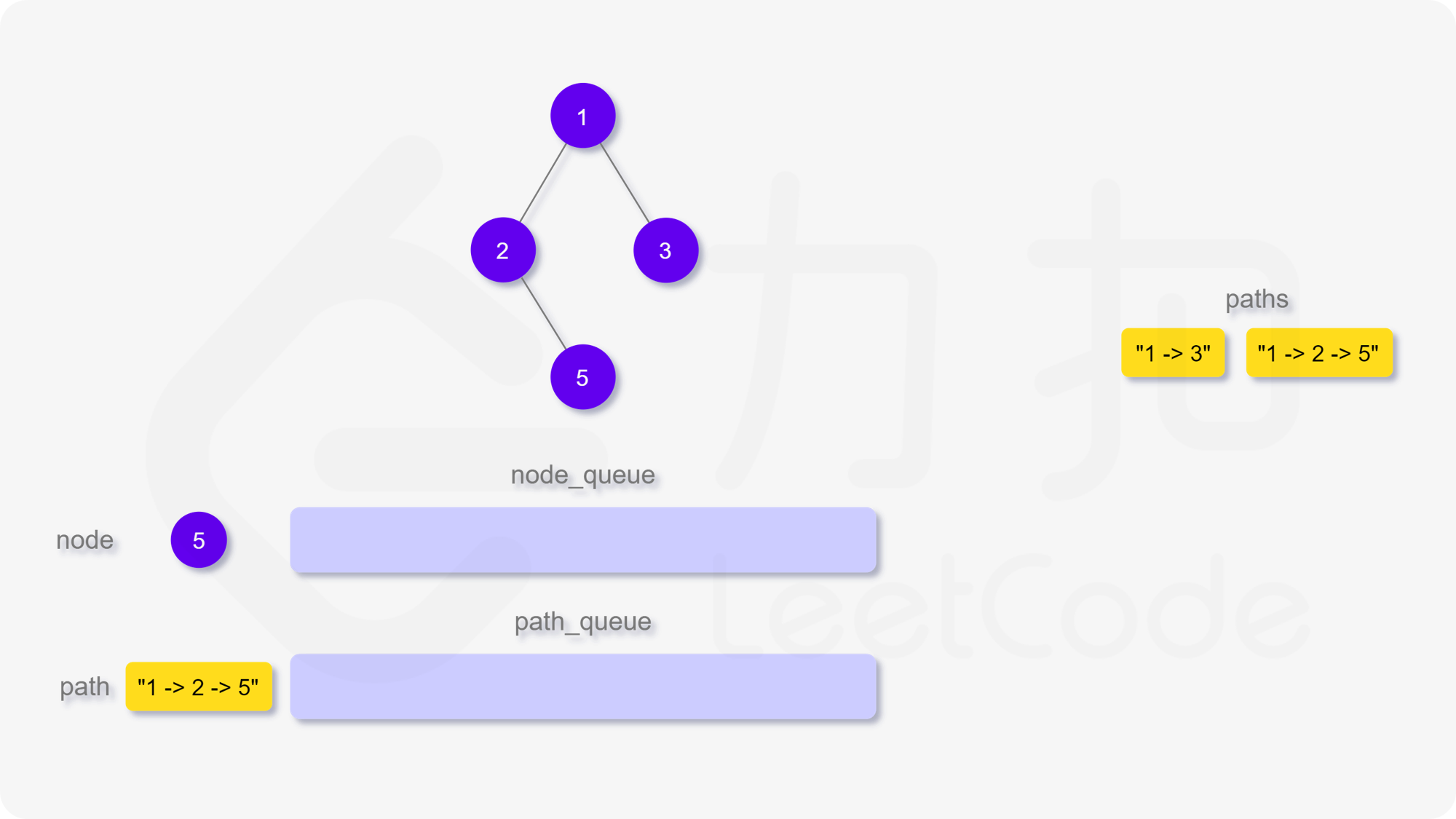
我们也可以用广度优先搜索来实现。我们维护一个队列,存储节点以及根到该节点的路径。一开始这个队列里只有根节点。在每一步迭代中,我们取出队列中的首节点,如果它是叶子节点,则将它对应的路径加入到答案中。如果它不是叶子节点,则将它的所有孩子节点加入到队列的末尾。当队列为空时广度优先搜索结束,我们即能得到答案。
< ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>
代码
[sol2-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| class Solution {
public:
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> paths;
if (root == nullptr) {
return paths;
}
queue<TreeNode*> node_queue;
queue<string> path_queue;
node_queue.push(root);
path_queue.push(to_string(root->val));
while (!node_queue.empty()) {
TreeNode* node = node_queue.front();
string path = path_queue.front();
node_queue.pop();
path_queue.pop();
if (node->left == nullptr && node->right == nullptr) {
paths.push_back(path);
} else {
if (node->left != nullptr) {
node_queue.push(node->left);
path_queue.push(path + "->" + to_string(node->left->val));
}
if (node->right != nullptr) {
node_queue.push(node->right);
path_queue.push(path + "->" + to_string(node->right->val));
}
}
}
return paths;
}
};
|
[sol2-JavaScript]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| var binaryTreePaths = function(root) {
const paths = [];
if (root === null) {
return paths;
}
const node_queue = [root];
const path_queue = [root.val.toString()];
while (node_queue.length) {
const node = node_queue.shift();
const path = path_queue.shift();
if (node.left === null && node.right === null) {
paths.push(path);
} else {
if (node.left !== null) {
node_queue.push(node.left);
path_queue.push(path + "->" + node.left.val.toString());
}
if (node.right !== null) {
node_queue.push(node.right);
path_queue.push(path + "->" + node.right.val.toString());
}
}
}
return paths;
};
|
[sol2-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| class Solution {
public List<String> binaryTreePaths(TreeNode root) {
List<String> paths = new ArrayList<String>();
if (root == null) {
return paths;
}
Queue<TreeNode> nodeQueue = new LinkedList<TreeNode>();
Queue<String> pathQueue = new LinkedList<String>();
nodeQueue.offer(root);
pathQueue.offer(Integer.toString(root.val));
while (!nodeQueue.isEmpty()) {
TreeNode node = nodeQueue.poll();
String path = pathQueue.poll();
if (node.left == null && node.right == null) {
paths.add(path);
} else {
if (node.left != null) {
nodeQueue.offer(node.left);
pathQueue.offer(new StringBuffer(path).append("->").append(node.left.val).toString());
}
if (node.right != null) {
nodeQueue.offer(node.right);
pathQueue.offer(new StringBuffer(path).append("->").append(node.right.val).toString());
}
}
}
return paths;
}
}
|
[sol2-Python]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution:
def binaryTreePaths(self, root: TreeNode) -> List[str]:
paths = list()
if not root:
return paths
node_queue = collections.deque([root])
path_queue = collections.deque([str(root.val)])
while node_queue:
node = node_queue.popleft()
path = path_queue.popleft()
if not node.left and not node.right:
paths.append(path)
else:
if node.left:
node_queue.append(node.left)
path_queue.append(path + '->' + str(node.left.val))
if node.right:
node_queue.append(node.right)
path_queue.append(path + '->' + str(node.right.val))
return paths
|
[sol2-Golang]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| func binaryTreePaths(root *TreeNode) []string {
paths := []string{}
if root == nil {
return paths
}
nodeQueue := []*TreeNode{}
pathQueue := []string{}
nodeQueue = append(nodeQueue, root)
pathQueue = append(pathQueue, strconv.Itoa(root.Val))
for i := 0; i < len(nodeQueue); i++ {
node, path := nodeQueue[i], pathQueue[i]
if node.Left == nil && node.Right == nil {
paths = append(paths, path)
continue
}
if node.Left != nil {
nodeQueue = append(nodeQueue, node.Left)
pathQueue = append(pathQueue, path + "->" + strconv.Itoa(node.Left.Val))
}
if node.Right != nil {
nodeQueue = append(nodeQueue, node.Right)
pathQueue = append(pathQueue, path + "->" + strconv.Itoa(node.Right.Val))
}
}
return paths
}
|
[sol2-C]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| char** binaryTreePaths(struct TreeNode* root, int* returnSize) {
char** paths = (char**)malloc(sizeof(char*) * 1001);
*returnSize = 0;
if (root == NULL) {
return paths;
}
struct TreeNode** node_queue = (struct TreeNode**)malloc(sizeof(struct TreeNode*) * 1001);
char** path_queue = (char**)malloc(sizeof(char*) * 1001);
int left = 0, right = 0;
char* tmp = malloc(sizeof(char) * 1001);
sprintf(tmp, "%d", root->val);
node_queue[right] = root;
path_queue[right++] = tmp;
while (left < right) {
struct TreeNode* node = node_queue[left];
char* path = path_queue[left++];
if (node->left == NULL && node->right == NULL) {
paths[(*returnSize)++] = path;
} else {
int n = strlen(path);
if (node->left != NULL) {
char* tmp = malloc(sizeof(char) * 1001);
for (int i = 0; i < n; i++) {
tmp[i] = path[i];
}
sprintf(tmp + n, "->%d", node->left->val);
node_queue[right] = node->left;
path_queue[right++] = tmp;
}
if (node->right != NULL) {
char* tmp = malloc(sizeof(char) * 1001);
for (int i = 0; i < n; i++) {
tmp[i] = path[i];
}
sprintf(tmp + n, "->%d", node->right->val);
node_queue[right] = node->right;
path_queue[right++] = tmp;
}
}
}
return paths;
}
|
复杂度分析
- 时间复杂度:$O(N^2)$,其中 $N$ 表示节点数目。分析同方法一。
- 空间复杂度:$O(N^2)$,其中 $N$ 表示节点数目。在最坏情况下,队列中会存在 $N$ 个节点,保存字符串的队列中每个节点的最大长度为 $N$,故空间复杂度为 $O(N^2)$。
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>