0300-最长递增子序列

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

**子序列 **是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组
[0,3,1,6,2,2,7] 的子序列。

示例 1：

**输入：** nums = [10,9,2,5,3,7,101,18]
**输出：** 4
**解释：** 最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：

**输入：** nums = [0,1,0,3,2,3]
**输出：** 4

示例 3：

**输入：** nums = [7,7,7,7,7,7,7]
**输出：** 1

提示：

• 1 <= nums.length <= 2500
• -104 <= nums[i] <= 104

进阶：

• 你能将算法的时间复杂度降低到 O(n log(n)) 吗?

方法一：动态规划

思路与算法

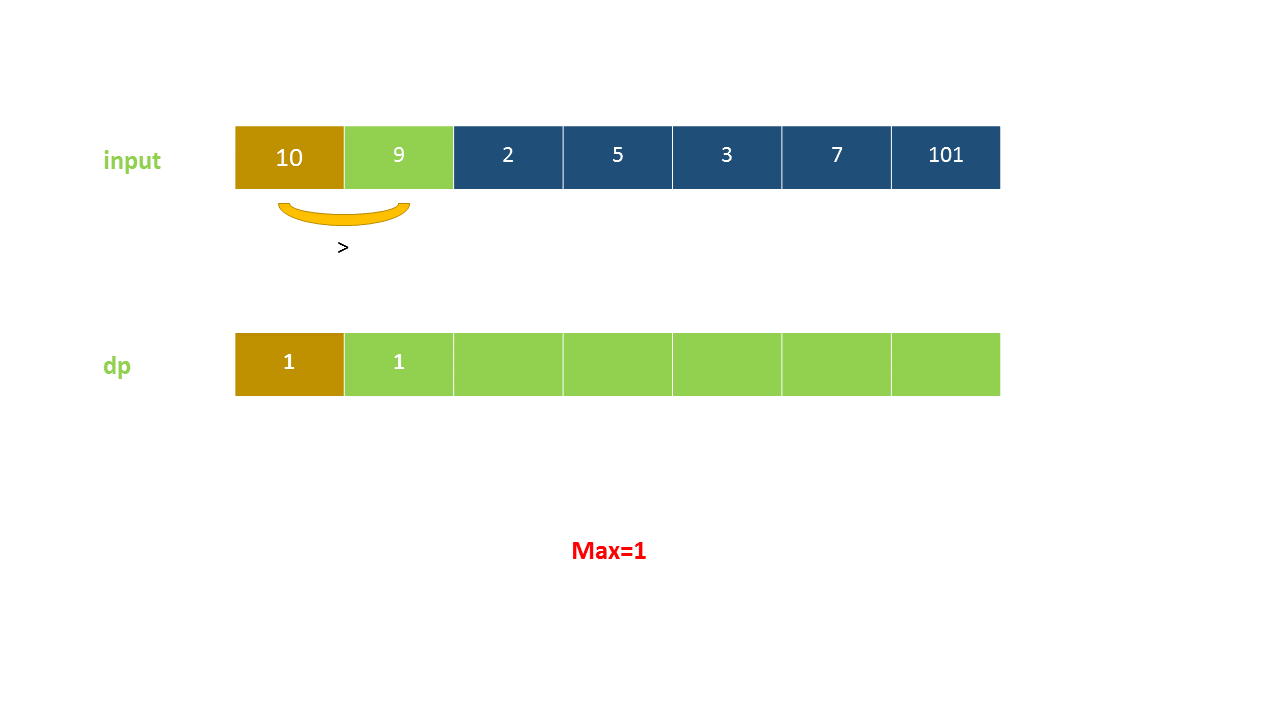
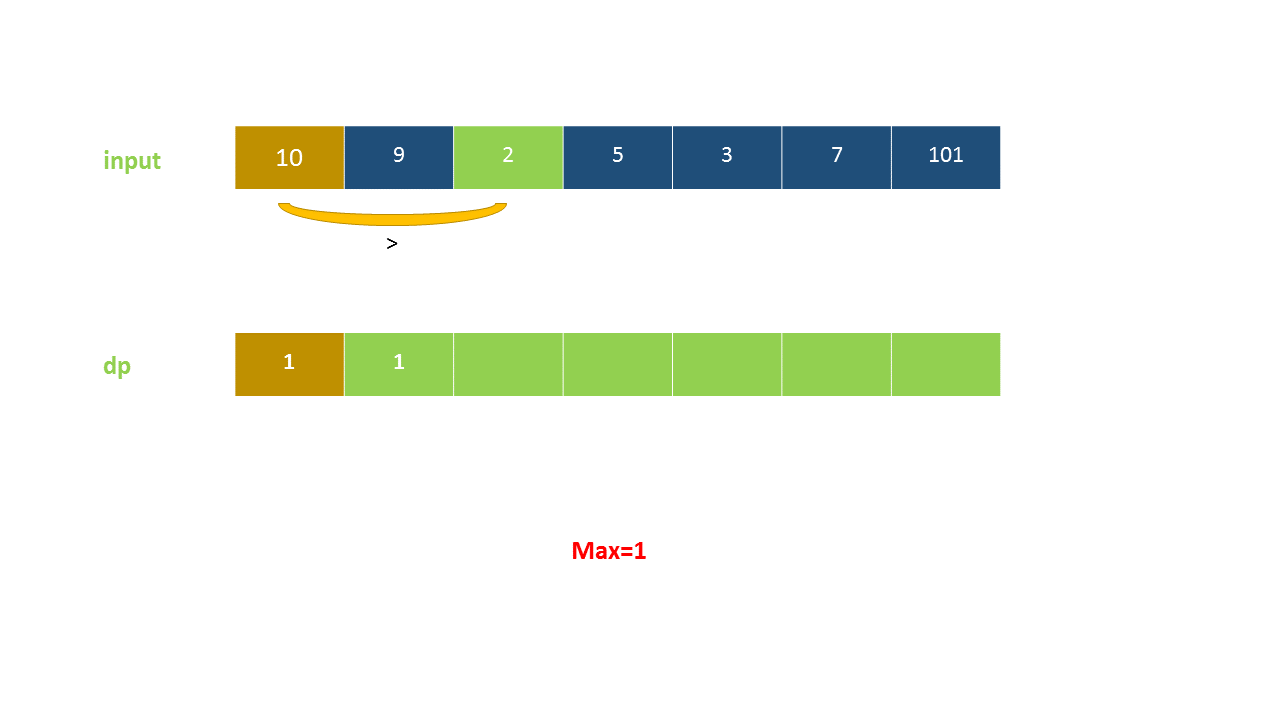
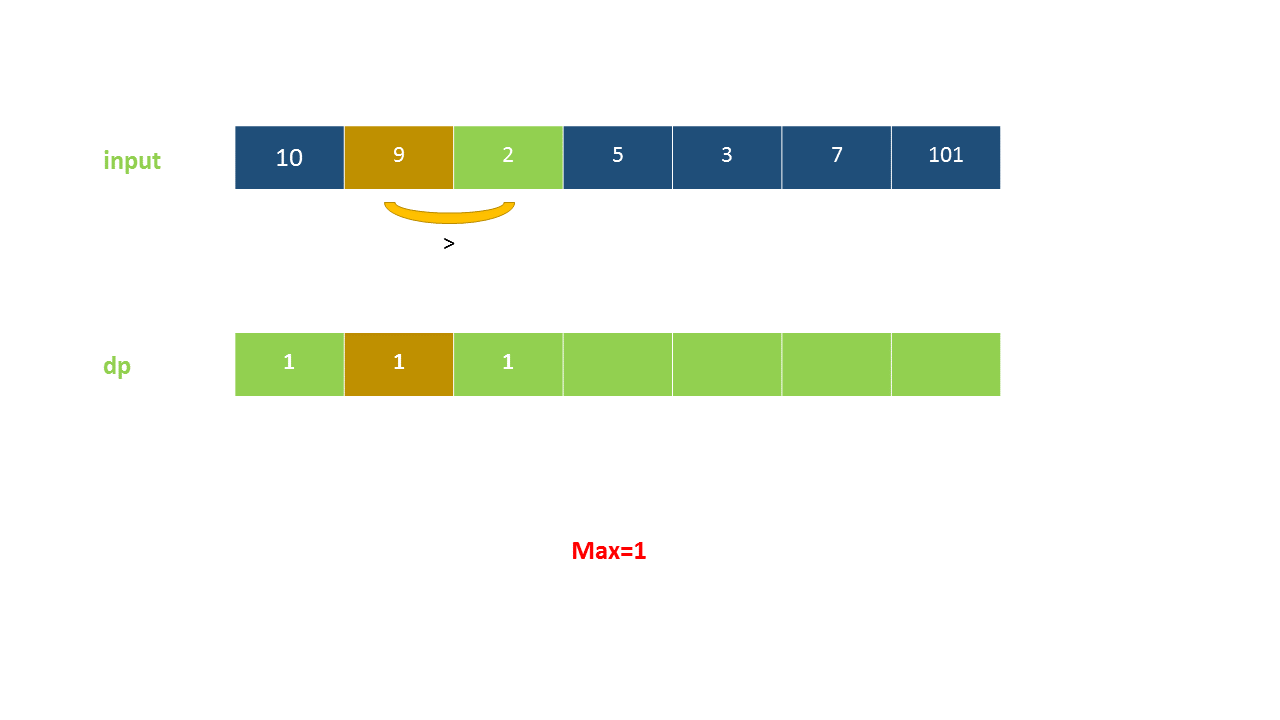
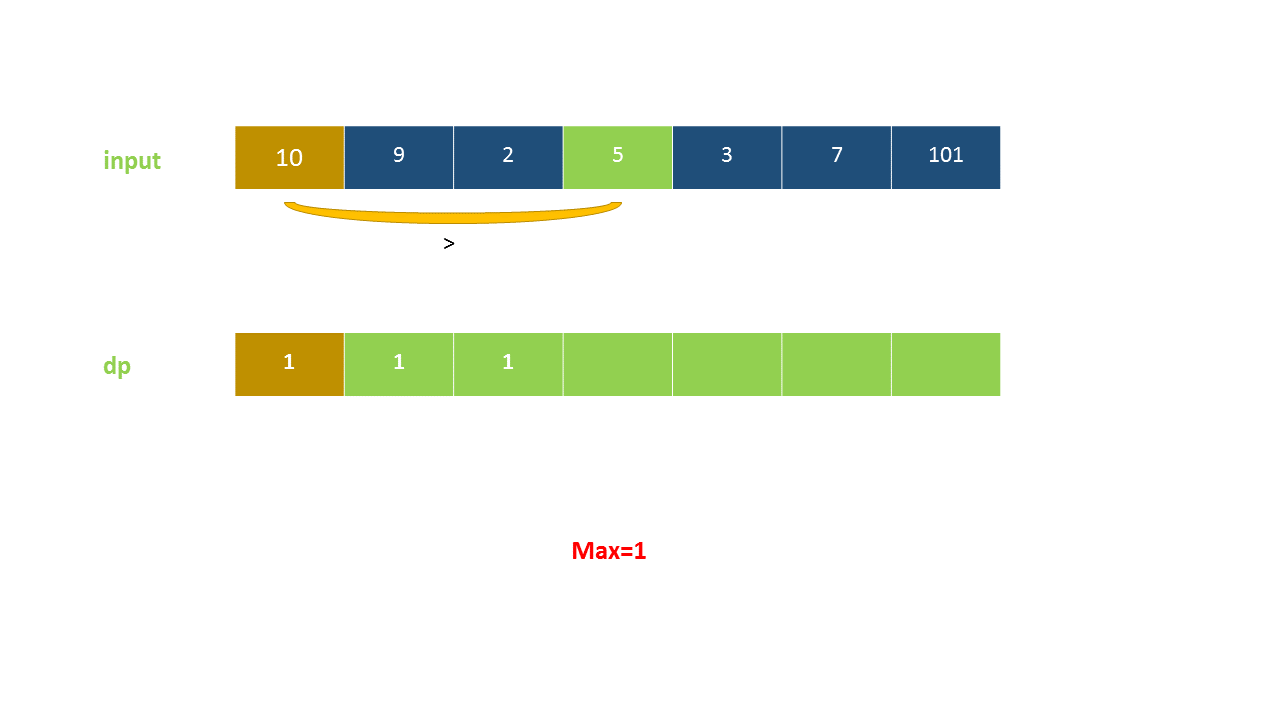
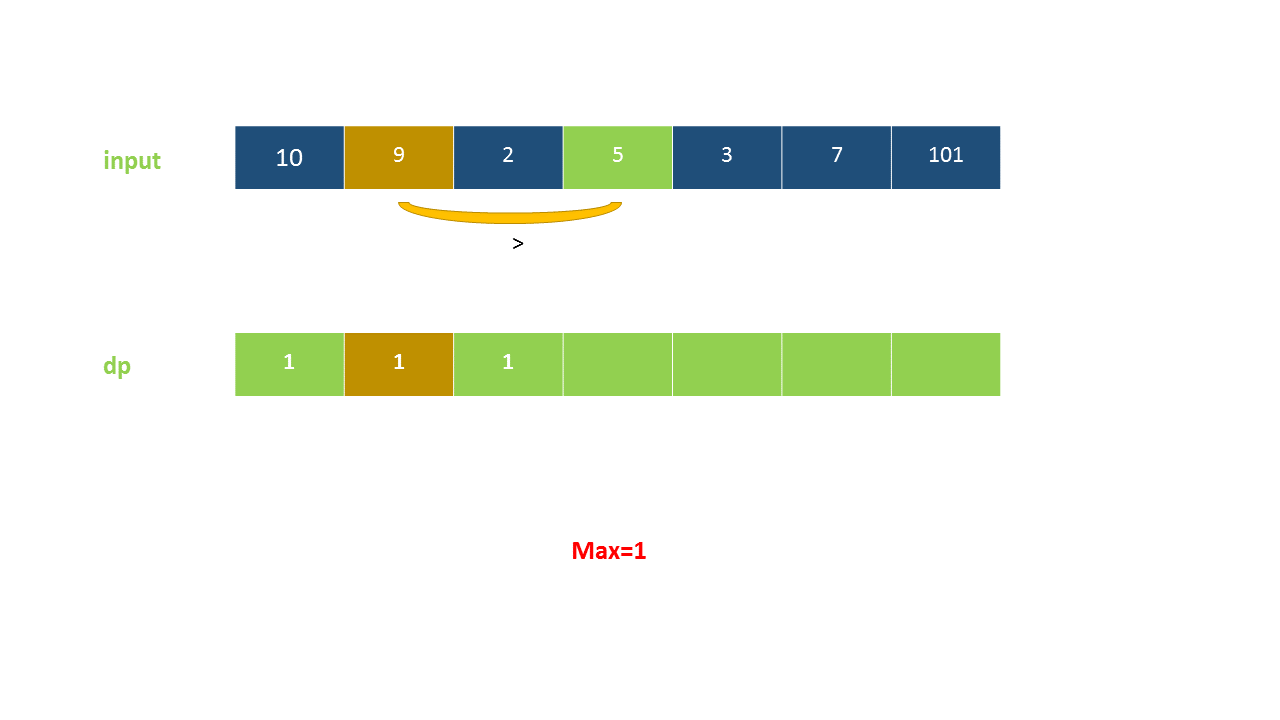
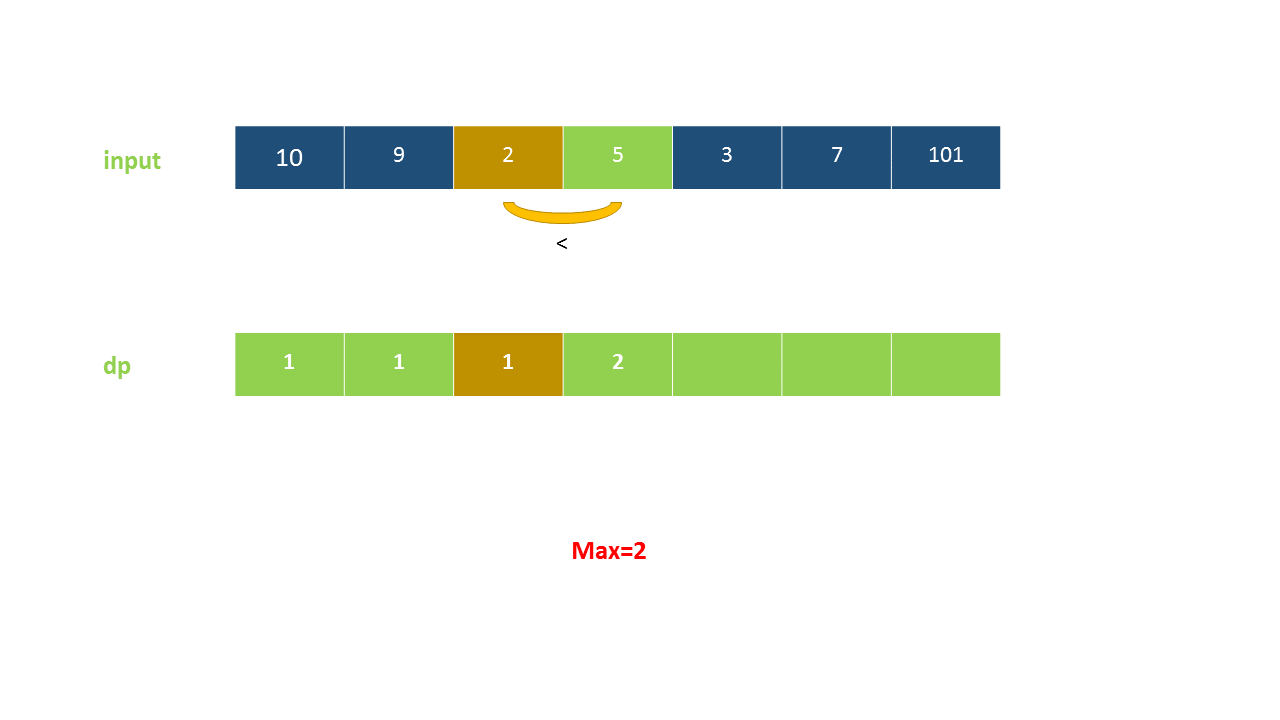
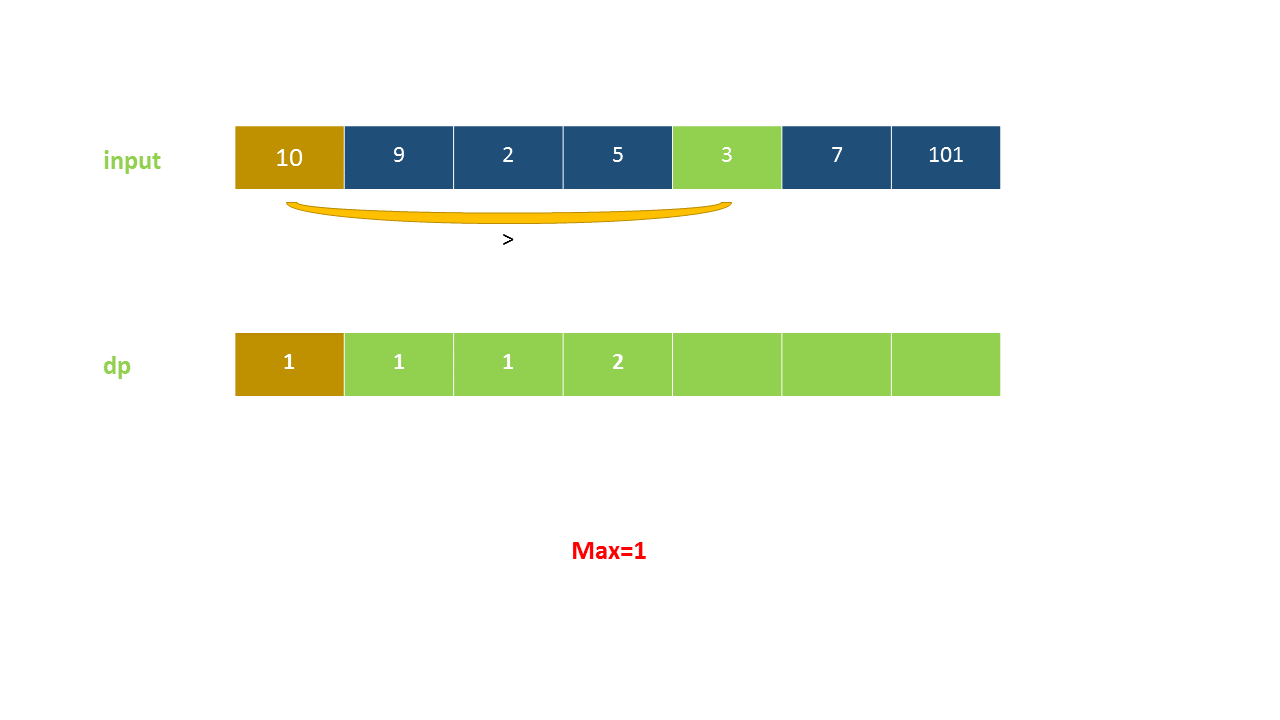
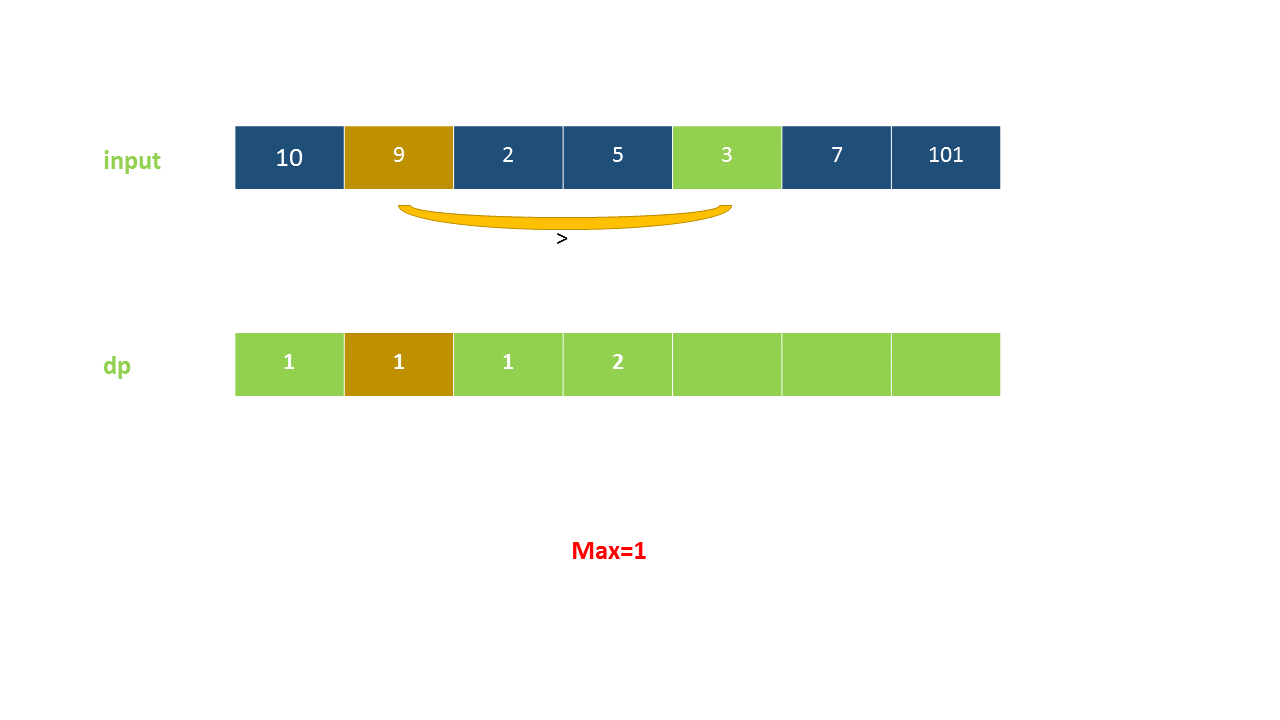
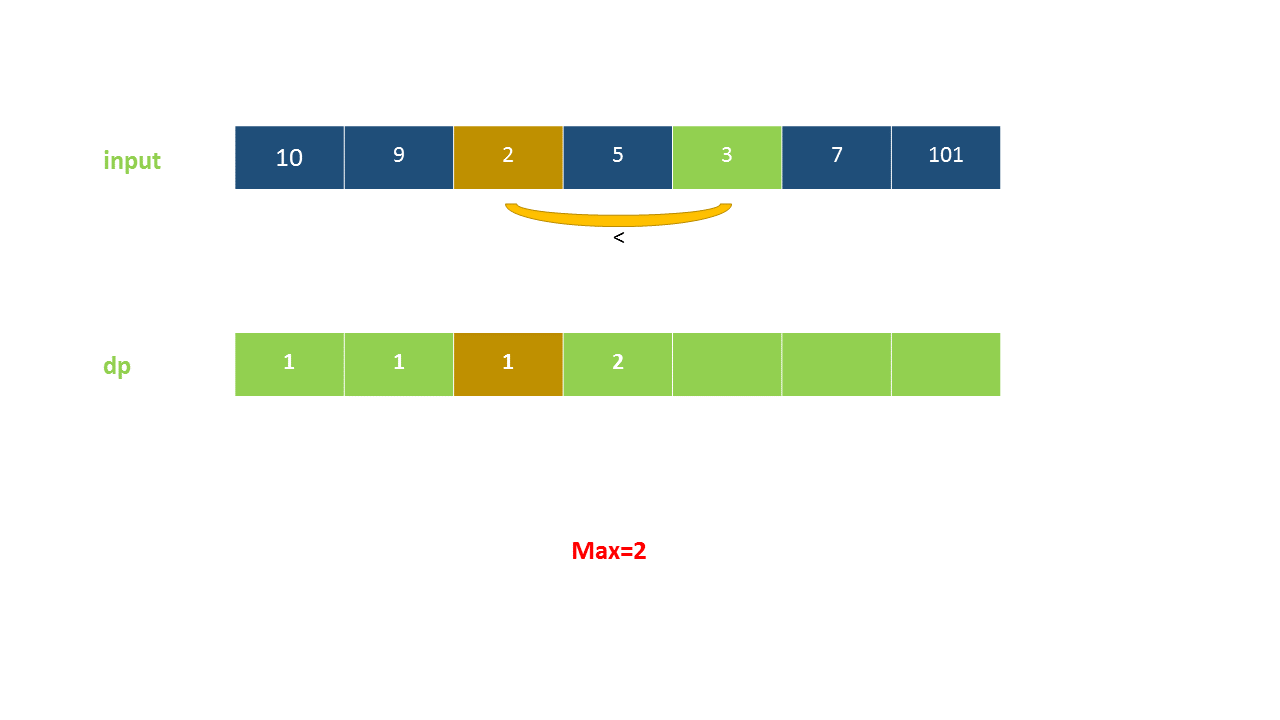
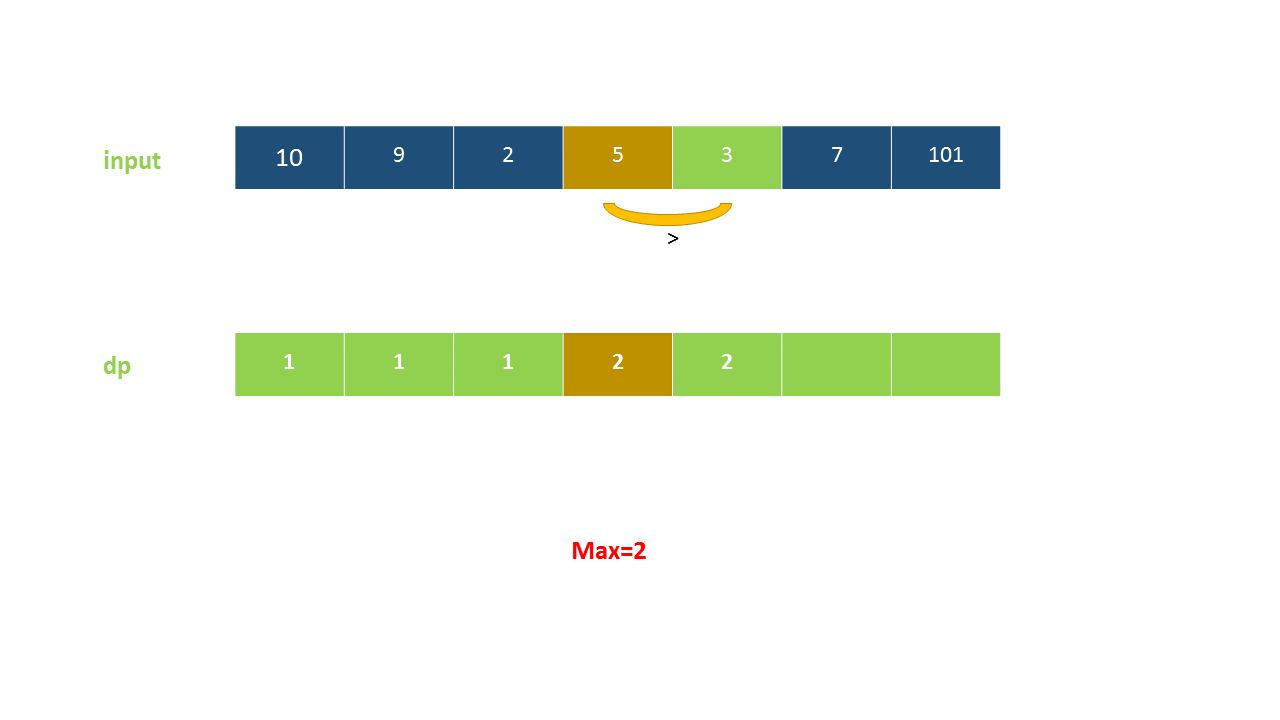
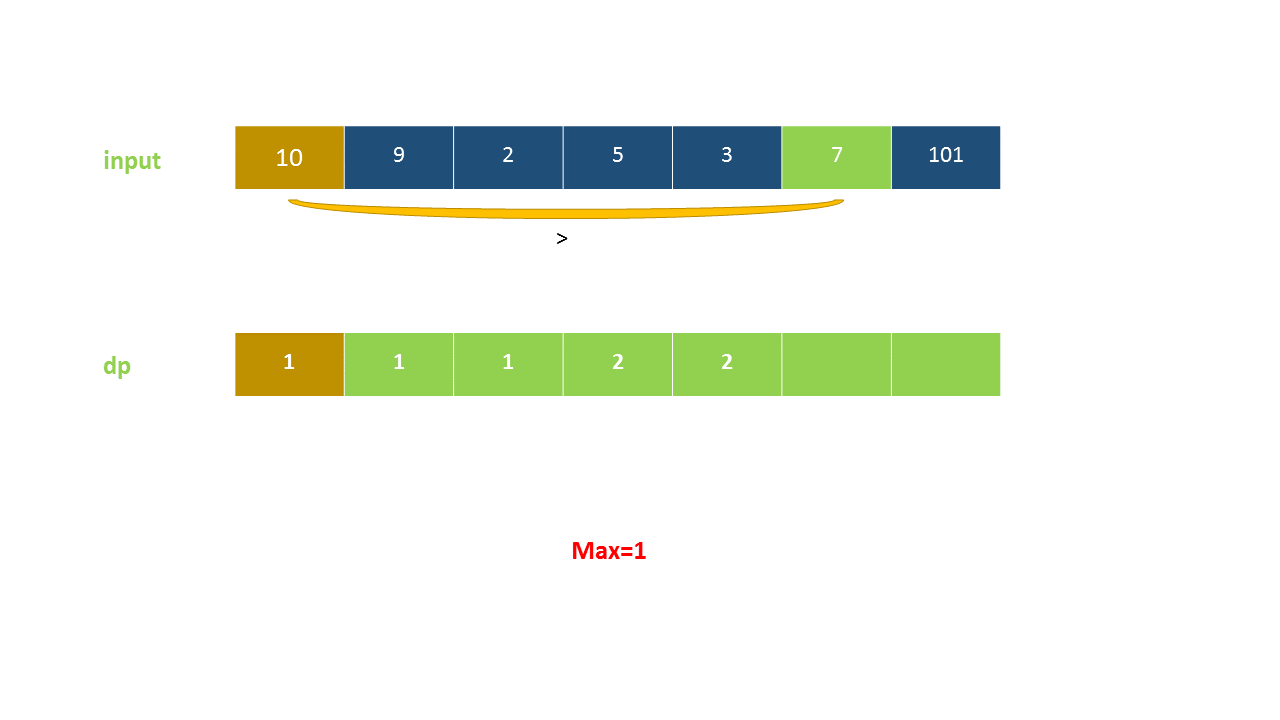
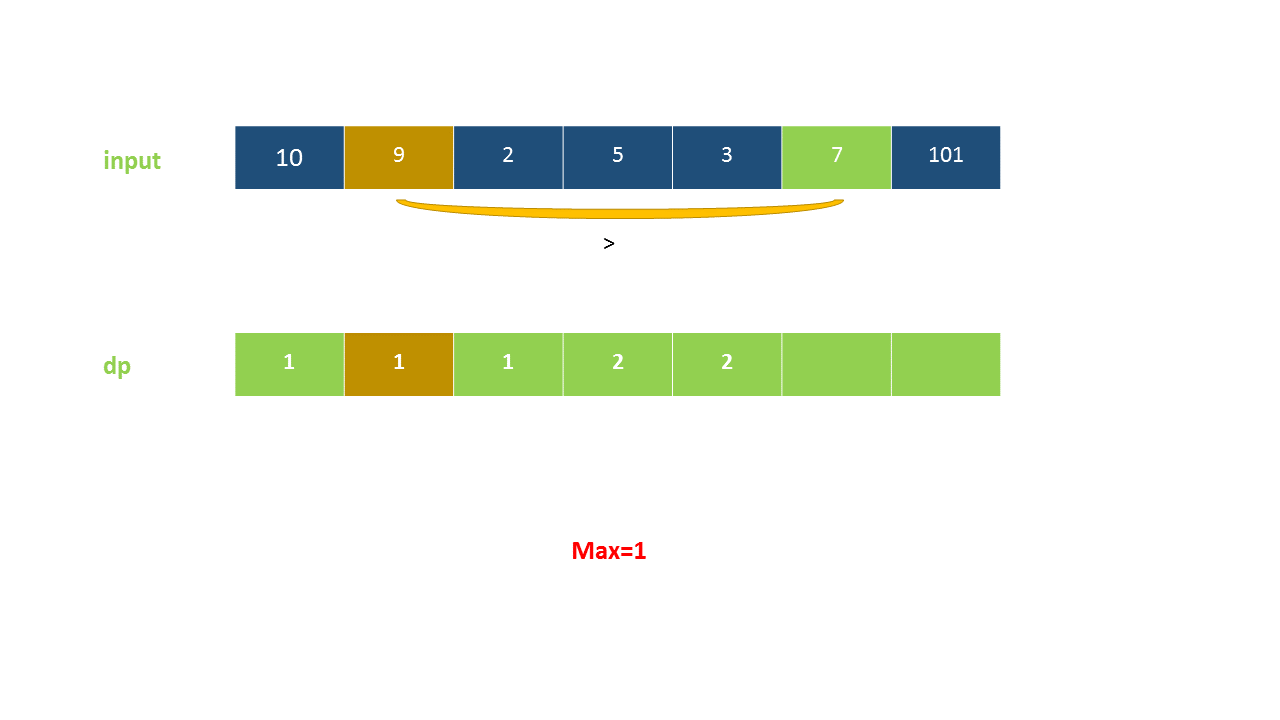
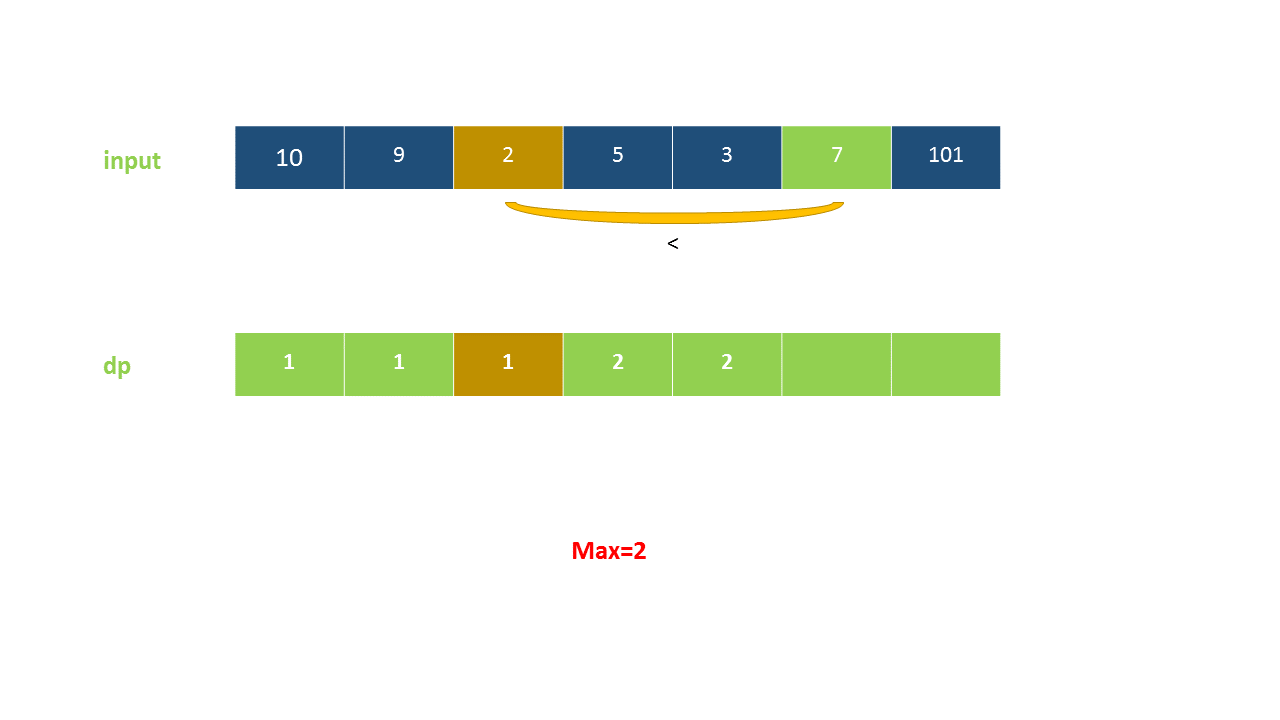
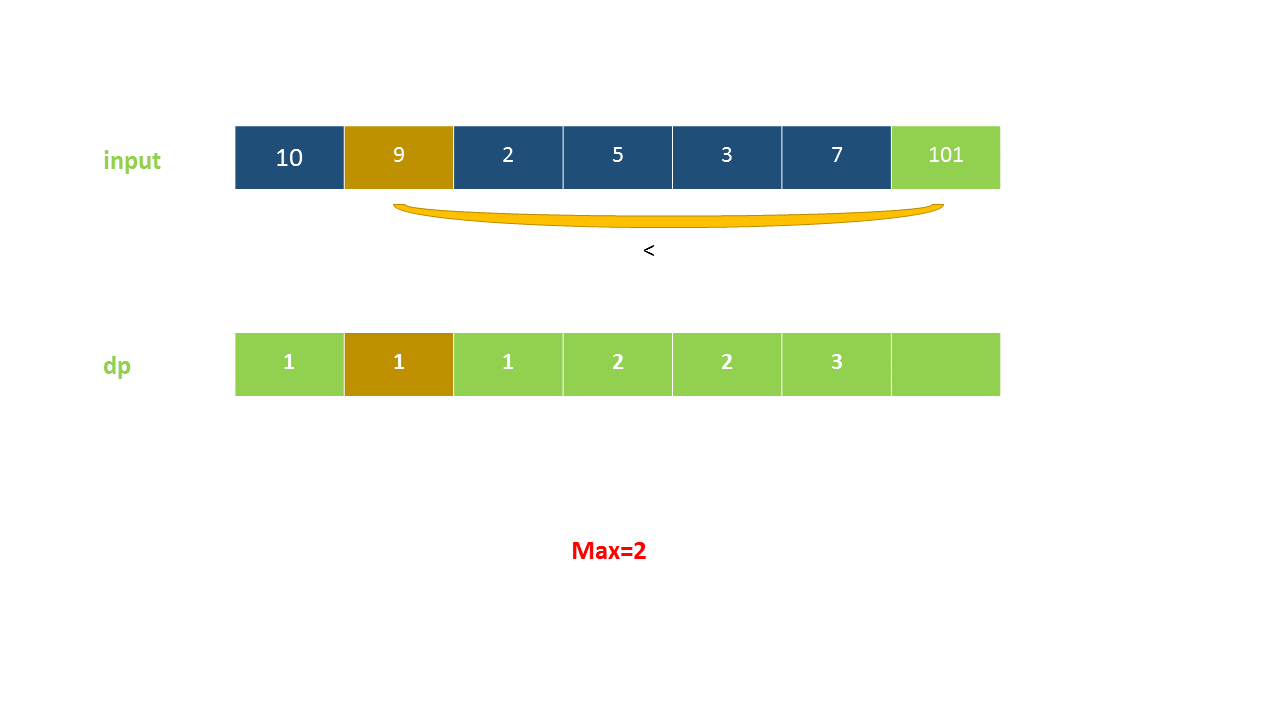
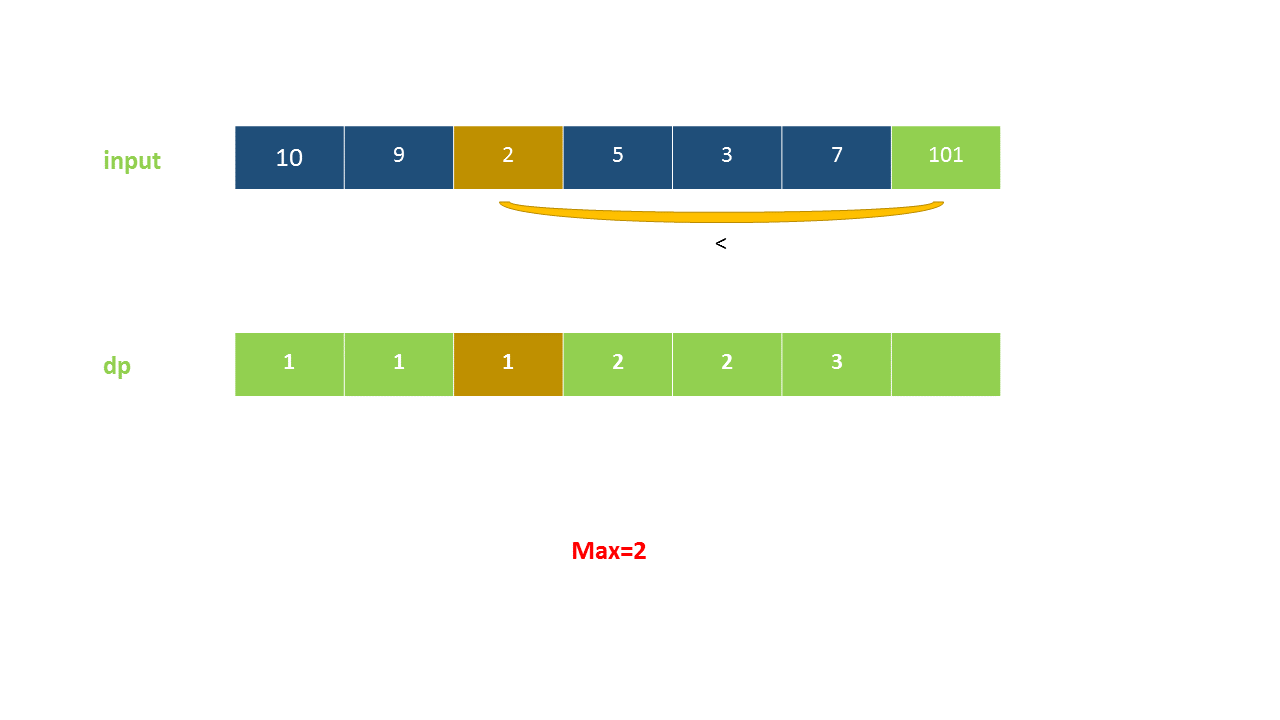
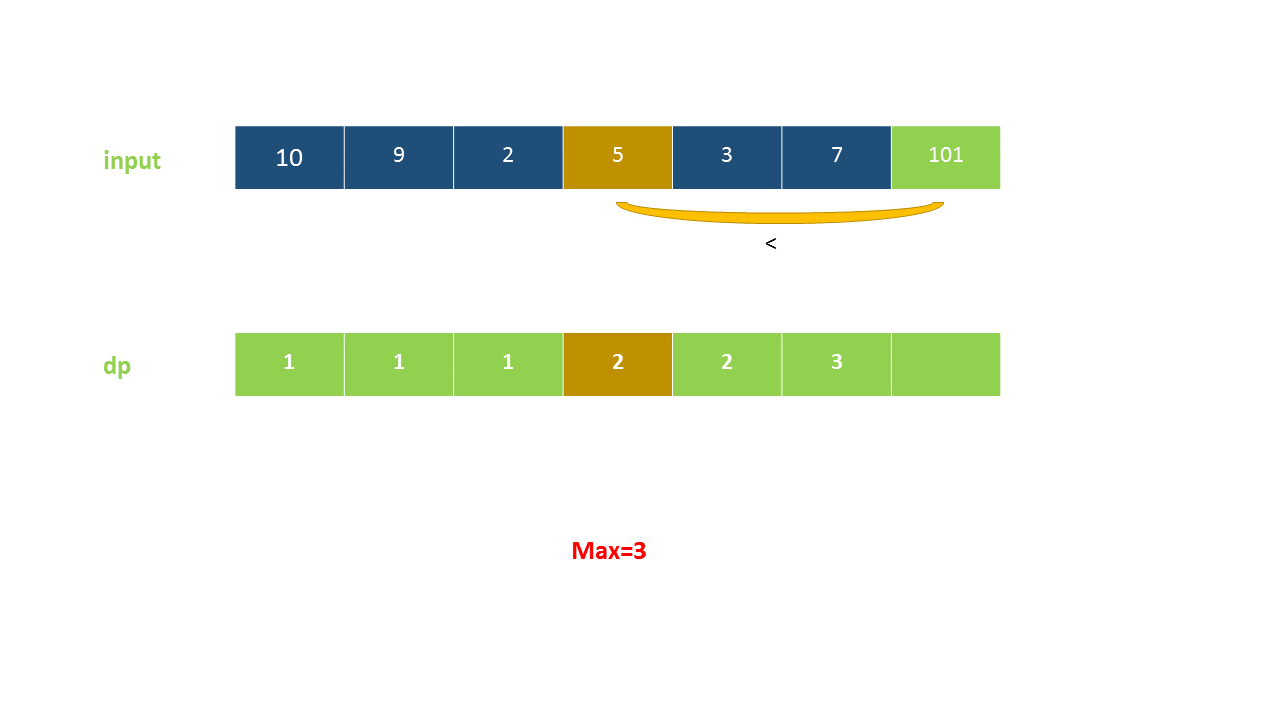
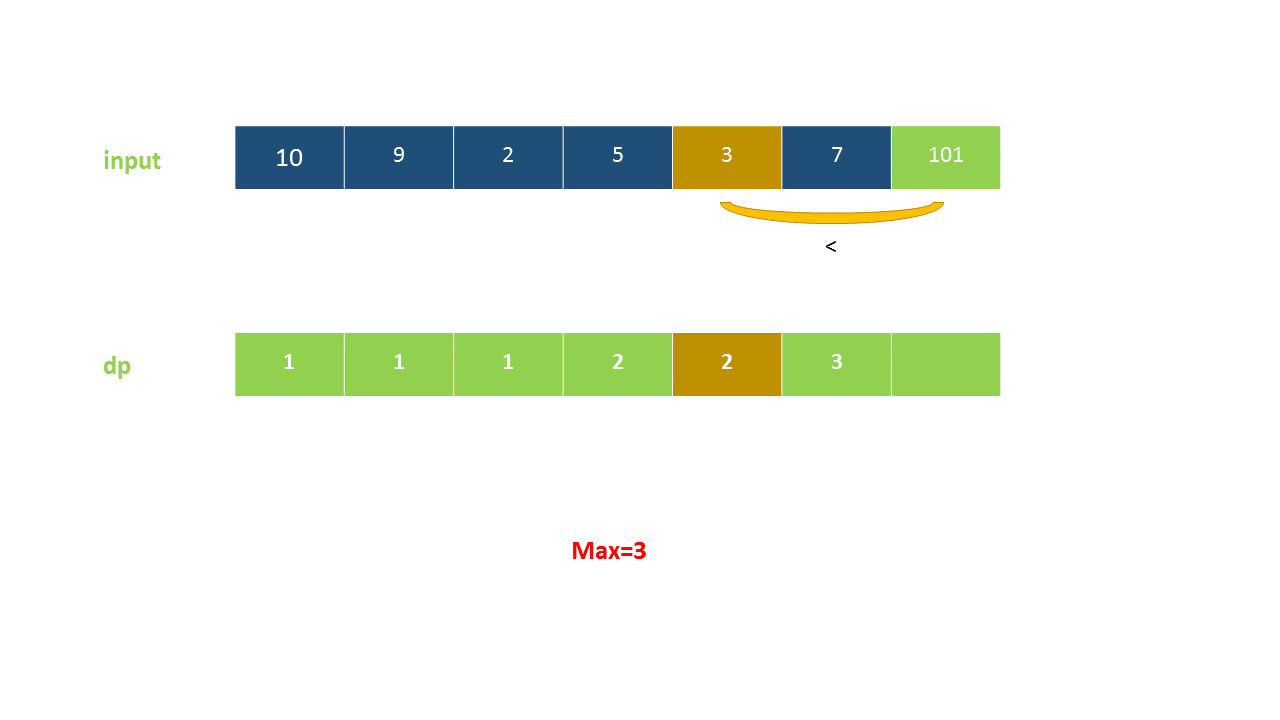
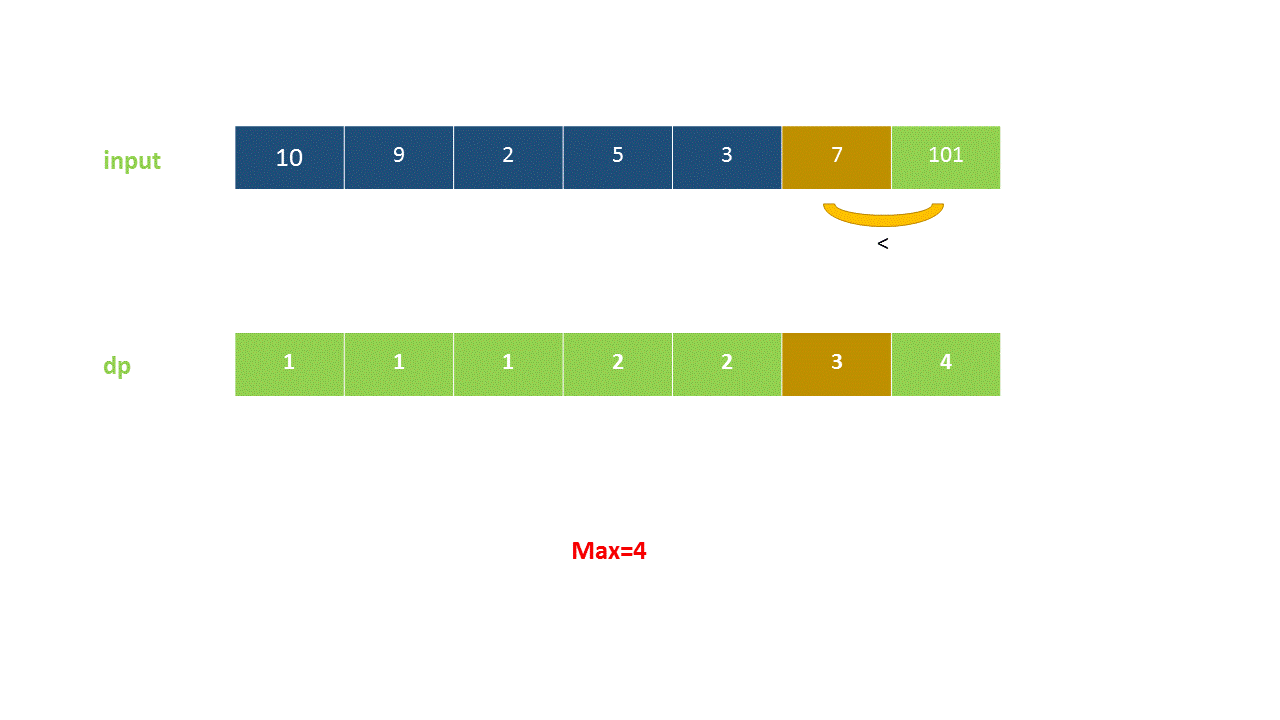
定义 dp}[i]$ 为考虑前 $i$ 个元素，以第 $i$ 个数字结尾的最长上升子序列的长度，注意 nums}[i]$ 必须被选取。

我们从小到大计算 dp 数组的值，在计算 dp}[i]$ 之前，我们已经计算出 dp}[0 \ldots i-1]$ 的值，则状态转移方程为：

$$
\textit{dp}[i] = \max(\textit{dp}[j]) + 1, \text{其中} , 0 \leq j < i , \text{且} , \textit{num}[j]<\textit{num}[i]
$$

即考虑往 dp}[0 \ldots i-1]$ 中最长的上升子序列后面再加一个 nums}[i]$。由于 dp}[j]$ 代表 nums}[0 \ldots j]$ 中以 nums}[j]$ 结尾的最长上升子序列，所以如果能从 dp}[j]$ 这个状态转移过来，那么 nums}[i]$ 必然要大于 nums}[j]$，才能将 nums}[i]$ 放在 nums}[j]$ 后面以形成更长的上升子序列。

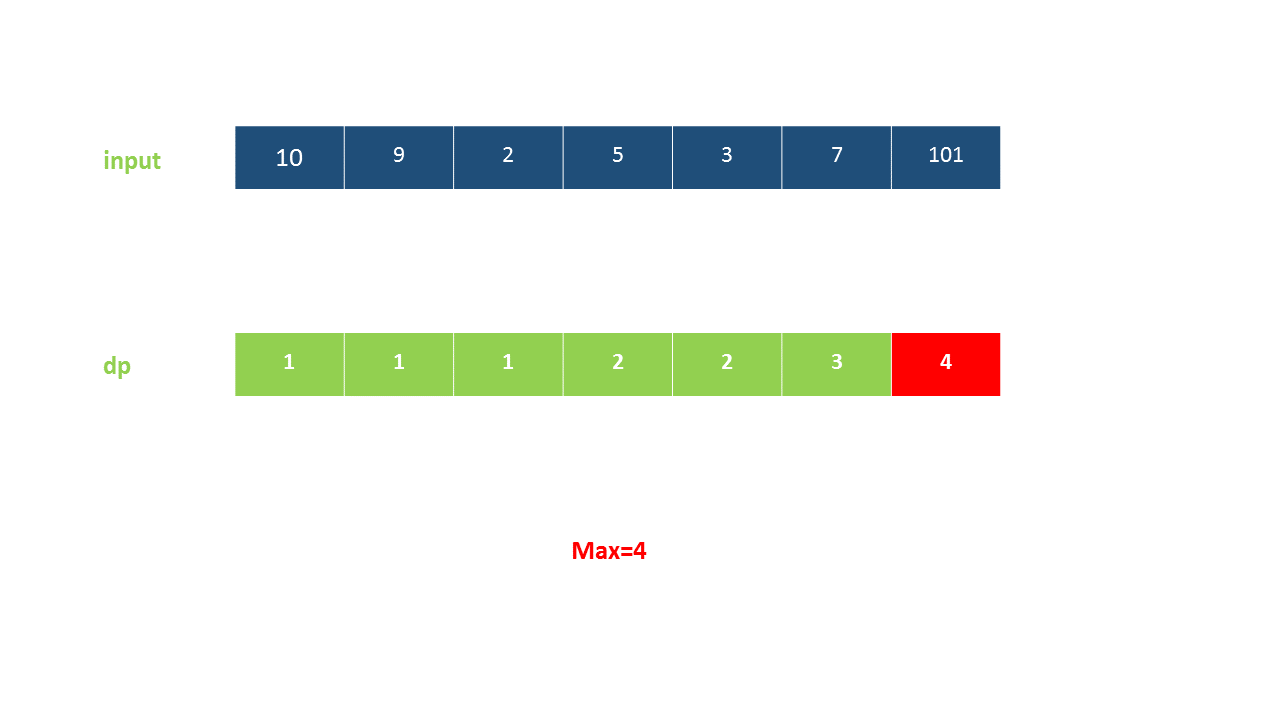
最后，整个数组的最长上升子序列即所有 dp}[i]$ 中的最大值。

$$
\text{LIS}_{\textit{length}}= \max(\textit{dp}[i]), \text{其中} , 0\leq i < n
$$

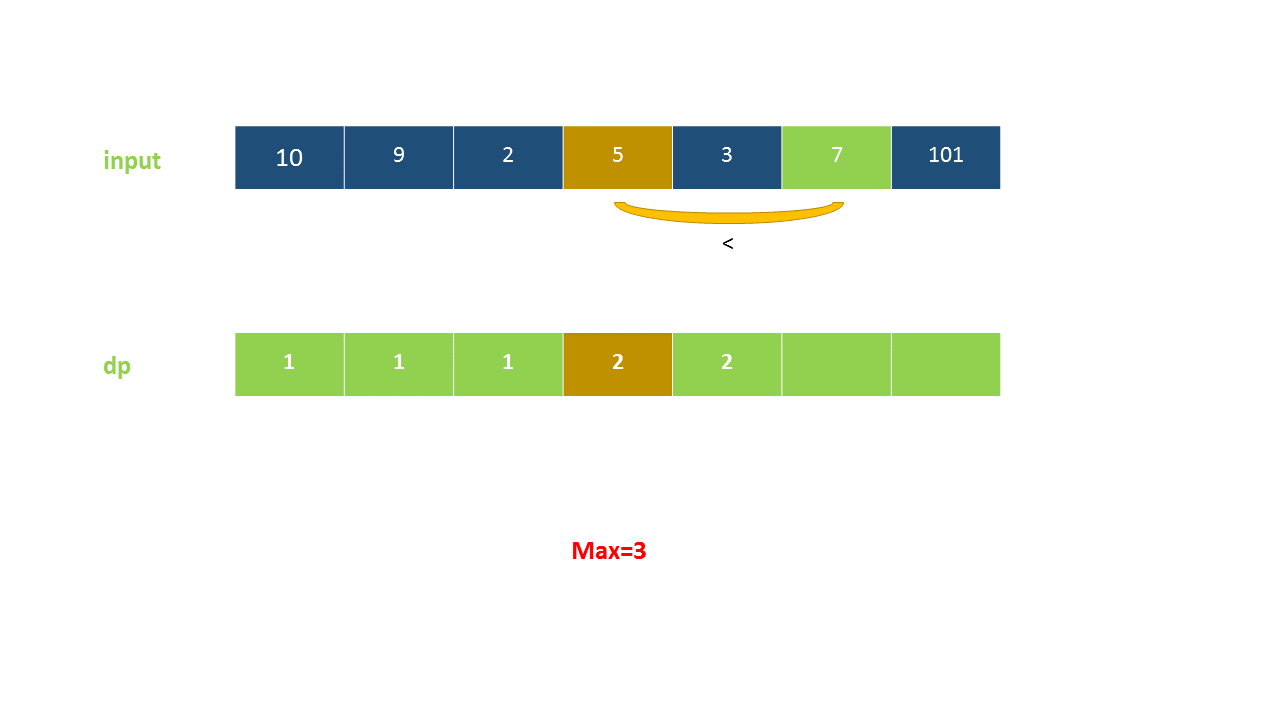
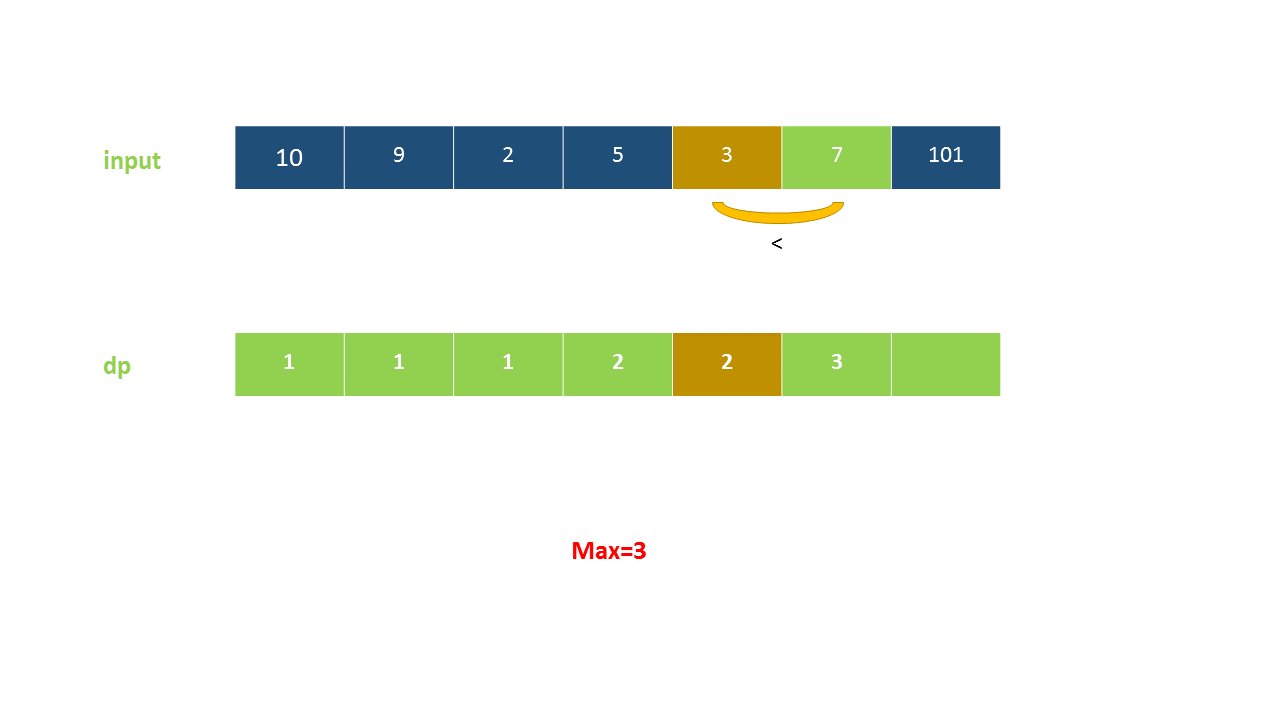
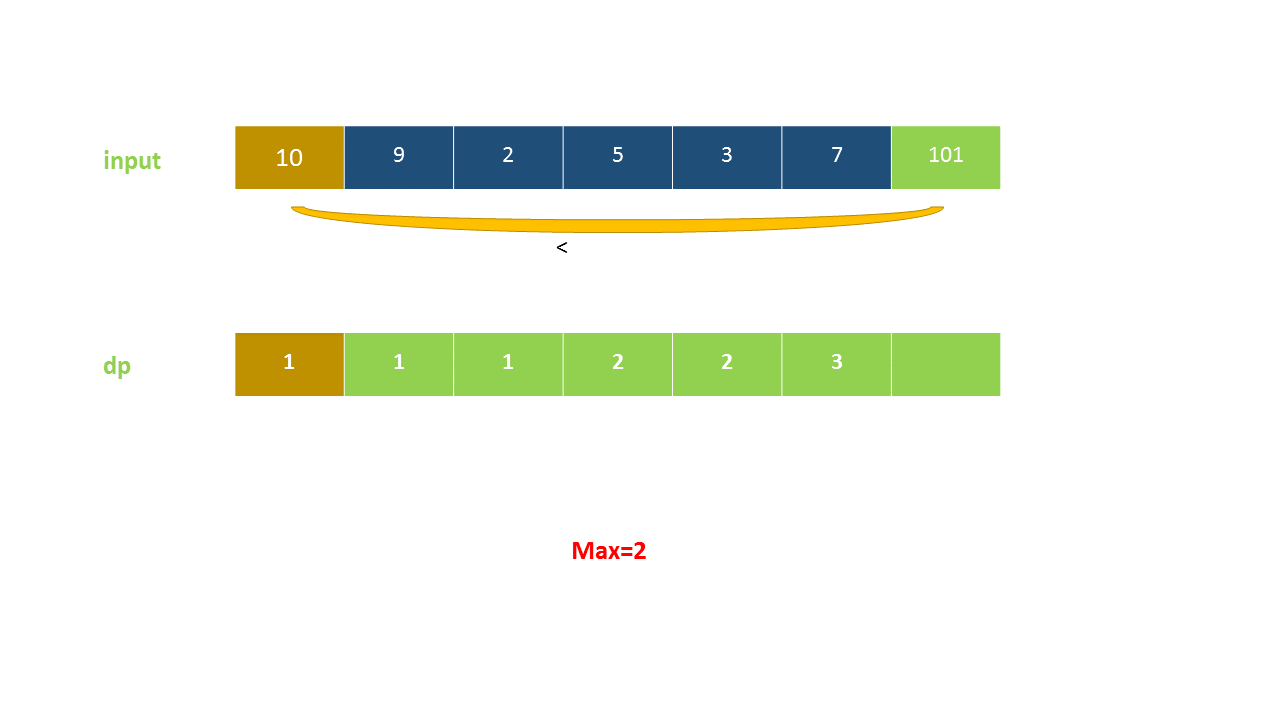
以下动画演示了该方法：

<,,,,,,,,,,,,,,,,,,,,,,>

[sol1-Java]

class Solution {
    public int lengthOfLIS(int[] nums) {
        if (nums.length == 0) {
            return 0;
        }
        int[] dp = new int[nums.length];
        dp[0] = 1;
        int maxans = 1;
        for (int i = 1; i < nums.length; i++) {
            dp[i] = 1;
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
            maxans = Math.max(maxans, dp[i]);
        }
        return maxans;
    }
}

[sol1-C++]

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n = (int)nums.size();
        if (n == 0) {
            return 0;
        }
        vector<int> dp(n, 0);
        for (int i = 0; i < n; ++i) {
            dp[i] = 1;
            for (int j = 0; j < i; ++j) {
                if (nums[j] < nums[i]) {
                    dp[i] = max(dp[i], dp[j] + 1);
                }
            }
        }
        return *max_element(dp.begin(), dp.end());
    }
};

[sol1-Python3]

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if not nums:
            return 0
        dp = []
        for i in range(len(nums)):
            dp.append(1)
            for j in range(i):
                if nums[i] > nums[j]:
                    dp[i] = max(dp[i], dp[j] + 1)
        return max(dp)

复杂度分析

• 时间复杂度：$O(n^2)$，其中 $n$ 为数组 nums 的长度。动态规划的状态数为 $n$，计算状态 $dp[i]$ 时，需要 $O(n)$ 的时间遍历 $dp[0 \ldots i-1]$ 的所有状态，所以总时间复杂度为 $O(n^2)$。

• 空间复杂度：$O(n)$，需要额外使用长度为 $n$ 的 $dp$ 数组。

方法二：贪心 + 二分查找

思路与算法

考虑一个简单的贪心，如果我们要使上升子序列尽可能的长，则我们需要让序列上升得尽可能慢，因此我们希望每次在上升子序列最后加上的那个数尽可能的小。

基于上面的贪心思路，我们维护一个数组 $d[i]$ ，表示长度为 $i$ 的最长上升子序列的末尾元素的最小值，用 len 记录目前最长上升子序列的长度，起始时 $len$ 为 $1$，$d[1] = \textit{nums}[0]$。

同时我们可以注意到 $d[i]$ 是关于 $i$ 单调递增的。因为如果 $d[j] \geq d[i]$ 且 $j < i$，我们考虑从长度为 $i$ 的最长上升子序列的末尾删除 $i-j$ 个元素，那么这个序列长度变为 $j$ ，且第 $j$ 个元素 $x$（末尾元素）必然小于 $d[i]$，也就小于 $d[j]$。那么我们就找到了一个长度为 $j$ 的最长上升子序列，并且末尾元素比 $d[j]$ 小，从而产生了矛盾。因此数组 $d$ 的单调性得证。

我们依次遍历数组 nums 中的每个元素，并更新数组 $d$ 和 $len$ 的值。如果 nums}[i] > d[\textit{len}]$ 则更新 $len = len + 1$，否则在 $d[1 \ldots len]$中找满足 $d[i - 1] < \textit{nums}[j] < d[i]$ 的下标 $i$，并更新 $d[i] = \textit{nums}[j]$。

根据 $d$ 数组的单调性，我们可以使用二分查找寻找下标 $i$，优化时间复杂度。

最后整个算法流程为：

• 设当前已求出的最长上升子序列的长度为 len（初始时为 $1$），从前往后遍历数组 nums，在遍历到 nums}[i]$ 时：

  • 如果 nums}[i] > d[\textit{len}]$ ，则直接加入到 $d$ 数组末尾，并更新 len} = \textit{len} + 1$；

  • 否则，在 $d$ 数组中二分查找，找到第一个比 nums}[i]$ 小的数 $d[k]$ ，并更新 $d[k + 1] = \textit{nums}[i]$。

以输入序列 $[0, 8, 4, 12, 2]$ 为例：

• 第一步插入 $0$，$d = [0]$；

• 第二步插入 $8$，$d = [0, 8]$；

• 第三步插入 $4$，$d = [0, 4]$；

• 第四步插入 $12$，$d = [0, 4, 12]$；

• 第五步插入 $2$，$d = [0, 2, 12]$。

最终得到最大递增子序列长度为 $3$。

[sol2-Java]

class Solution {
    public int lengthOfLIS(int[] nums) {
        int len = 1, n = nums.length;
        if (n == 0) {
            return 0;
        }
        int[] d = new int[n + 1];
        d[len] = nums[0];
        for (int i = 1; i < n; ++i) {
            if (nums[i] > d[len]) {
                d[++len] = nums[i];
            } else {
                int l = 1, r = len, pos = 0; // 如果找不到说明所有的数都比 nums[i] 大，此时要更新 d[1]，所以这里将 pos 设为 0
                while (l <= r) {
                    int mid = (l + r) >> 1;
                    if (d[mid] < nums[i]) {
                        pos = mid;
                        l = mid + 1;
                    } else {
                        r = mid - 1;
                    }
                }
                d[pos + 1] = nums[i];
            }
        }
        return len;
    }
}

[sol2-C++]

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int len = 1, n = (int)nums.size();
        if (n == 0) {
            return 0;
        }
        vector<int> d(n + 1, 0);
        d[len] = nums[0];
        for (int i = 1; i < n; ++i) {
            if (nums[i] > d[len]) {
                d[++len] = nums[i];
            } else {
                int l = 1, r = len, pos = 0; // 如果找不到说明所有的数都比 nums[i] 大，此时要更新 d[1]，所以这里将 pos 设为 0
                while (l <= r) {
                    int mid = (l + r) >> 1;
                    if (d[mid] < nums[i]) {
                        pos = mid;
                        l = mid + 1;
                    } else {
                        r = mid - 1;
                    }
                }
                d[pos + 1] = nums[i];
            }
        }
        return len;
    }
};

[sol2-Python3]

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        d = []
        for n in nums:
            if not d or n > d[-1]:
                d.append(n)
            else:
                l, r = 0, len(d) - 1
                loc = r
                while l <= r:
                    mid = (l + r) // 2
                    if d[mid] >= n:
                        loc = mid
                        r = mid - 1
                    else:
                        l = mid + 1
                d[loc] = n
        return len(d)

复杂度分析

• 时间复杂度：$O(n\log n)$。数组 nums 的长度为 $n$，我们依次用数组中的元素去更新 $d$ 数组，而更新 $d$ 数组时需要进行 $O(\log n)$ 的二分搜索，所以总时间复杂度为 $O(n\log n)$。

• 空间复杂度：$O(n)$，需要额外使用长度为 $n$ 的 $d$ 数组。