给定一个二维矩阵 matrix,以下类型的多个请求:
计算其子矩形范围内元素的总和,该子矩阵的 左上角 为 (row1, col1) , 右下角 为 (row2, col2) 。
实现 NumMatrix 类:
NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、 右下角 (row2, col2) 所描述的子矩阵的元素 总和 。
示例 1:
**输入:**
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
**输出:**
[null, 8, 11, 12]
**解释:**
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]);
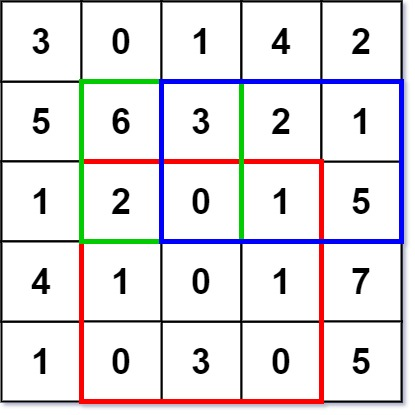
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 200-105 <= matrix[i][j] <= 1050 <= row1 <= row2 < m0 <= col1 <= col2 < n最多调用 104 次 sumRegion 方法
前言 这道题是「303. 区域和检索 - 数组不可变 」的进阶,第 303 题是在一维数组中做区域和检索,这道题是在二维矩阵中做区域和检索。
这道题有两种解法,分别是对每一行计算一维前缀和,以及对整个矩阵计算二维前缀和。
方法一:一维前缀和 第 303 题中,初始化时对数组计算前缀和,每次检索即可在 $O(1)$ 的时间内得到结果。可以将第 303 题的做法应用于这道题,初始化时对矩阵的每一行计算前缀和,检索时对二维区域中的每一行计算子数组和,然后对每一行的子数组和计算总和。
具体实现方面,创建 $m$ 行 $n+1$ 列的二维数组 sums,其中 $m$ 和 $n$ 分别是矩阵 matrix 的行数和列数,sums}[i]$ 为 matrix}[i]$ 的前缀和数组。将 sums 的列数设为 $n+1$ 的目的是为了方便计算每一行的子数组和,不需要对 col}_1=0$ 的情况特殊处理。
[sol1-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class NumMatrix { int [][] sums; public NumMatrix (int [][] matrix) { int m = matrix.length; if (m > 0 ) { int n = matrix[0 ].length; sums = new int [m][n + 1 ]; for (int i = 0 ; i < m; i++) { for (int j = 0 ; j < n; j++) { sums[i][j + 1 ] = sums[i][j] + matrix[i][j]; } } } } public int sumRegion (int row1, int col1, int row2, int col2) { int sum = 0 ; for (int i = row1; i <= row2; i++) { sum += sums[i][col2 + 1 ] - sums[i][col1]; } return sum; } }
[sol1-JavaScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 var NumMatrix = function (matrix ) { const m = matrix.length ; if (m > 0 ) { const n = matrix[0 ].length ; this .sums = new Array (m).fill (0 ).map (() => new Array (n + 1 ).fill (0 )); for (let i = 0 ; i < m; i++) { for (let j = 0 ; j < n; j++) { this .sums [i][j + 1 ] = this .sums [i][j] + matrix[i][j]; } } } }; NumMatrix .prototype sumRegion = function (row1, col1, row2, col2 ) { let sum = 0 ; for (let i = row1; i <= row2; i++) { sum += this .sums [i][col2 + 1 ] - this .sums [i][col1]; } return sum; };
[sol1-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 type NumMatrix struct { sums [][]int } func Constructor (matrix [][]int ) sums := make ([][]int , len (matrix)) for i, row := range matrix { sums[i] = make ([]int , len (row)+1 ) for j, v := range row { sums[i][j+1 ] = sums[i][j] + v } } return NumMatrix{sums} } func (nm *NumMatrix) int ) (sum int ) { for i := row1; i <= row2; i++ { sum += nm.sums[i][col2+1 ] - nm.sums[i][col1] } return }
[sol1-Python3] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class NumMatrix : def __init__ (self, matrix: List [List [int ]] ): m, n = len (matrix), (len (matrix[0 ]) if matrix else 0 ) self.sums = [[0 ] * (n + 1 ) for _ in range (m)] _sums = self.sums for i in range (m): for j in range (n): _sums[i][j + 1 ] = _sums[i][j] + matrix[i][j] def sumRegion (self, row1: int , col1: int , row2: int , col2: int ) -> int : _sums = self.sums total = sum (_sums[i][col2 + 1 ] - _sums[i][col1] for i in range (row1, row2 + 1 )) return total
[sol1-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class NumMatrix {public : vector<vector<int >> sums; NumMatrix (vector<vector<int >>& matrix) { int m = matrix.size (); if (m > 0 ) { int n = matrix[0 ].size (); sums.resize (m, vector <int >(n + 1 )); for (int i = 0 ; i < m; i++) { for (int j = 0 ; j < n; j++) { sums[i][j + 1 ] = sums[i][j] + matrix[i][j]; } } } } int sumRegion (int row1, int col1, int row2, int col2) int sum = 0 ; for (int i = row1; i <= row2; i++) { sum += sums[i][col2 + 1 ] - sums[i][col1]; } return sum; } };
[sol1-C] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 typedef struct { int ** sums; int sumsSize; } NumMatrix; NumMatrix* numMatrixCreate (int ** matrix, int matrixSize, int * matrixColSize) { NumMatrix* ret = malloc (sizeof (NumMatrix)); ret->sums = malloc (sizeof (int *) * matrixSize); ret->sumsSize = matrixSize; for (int i = 0 ; i < matrixSize; i++) { ret->sums[i] = malloc (sizeof (int ) * (matrixColSize[i] + 1 )); ret->sums[i][0 ] = 0 ; for (int j = 0 ; j < matrixColSize[i]; j++) { ret->sums[i][j + 1 ] = ret->sums[i][j] + matrix[i][j]; } } return ret; } int numMatrixSumRegion (NumMatrix* obj, int row1, int col1, int row2, int col2) { int sum = 0 ; for (int i = row1; i <= row2; i++) { sum += obj->sums[i][col2 + 1 ] - obj->sums[i][col1]; } return sum; } void numMatrixFree (NumMatrix* obj) { for (int i = 0 ; i < obj->sumsSize; i++) { free (obj->sums[i]); } free (obj->sums); }
复杂度分析
时间复杂度:初始化 $O(mn)$,每次检索 $O(m)$,其中 $m$ 和 $n$ 分别是矩阵 matrix 的行数和列数。
空间复杂度:$O(mn)$,其中 $m$ 和 $n$ 分别是矩阵 matrix 的行数和列数。需要创建一个 $m$ 行 $n+1$ 列的前缀和数组 sums。
方法二:二维前缀和 方法一虽然利用了前缀和,但是每次检索的时间复杂度是 $O(m)$,仍然没有降到 $O(1)$。为了将每次检索的时间复杂度降到 $O(1)$,需要使用二维前缀和,在初始化的时候计算二维前缀和数组。
假设 $m$ 和 $n$ 分别是矩阵 matrix 的行数和列数。定义当 $0 \le i<m$ 且 $0 \le j<n$ 时,$f(i,j)$ 为矩阵 matrix 的以 $(i,j)$ 为右下角的子矩阵的元素之和:
$$
当 $i=0$ 或 $j=0$ 时,计算 $f(i,j)$ 只需要对矩阵 matrix 的最上边的行和最左边的列分别计算前缀和即可。当 $i$ 和 $j$ 都大于 $0$ 时,如何计算 $f(i,j)$ 的值?
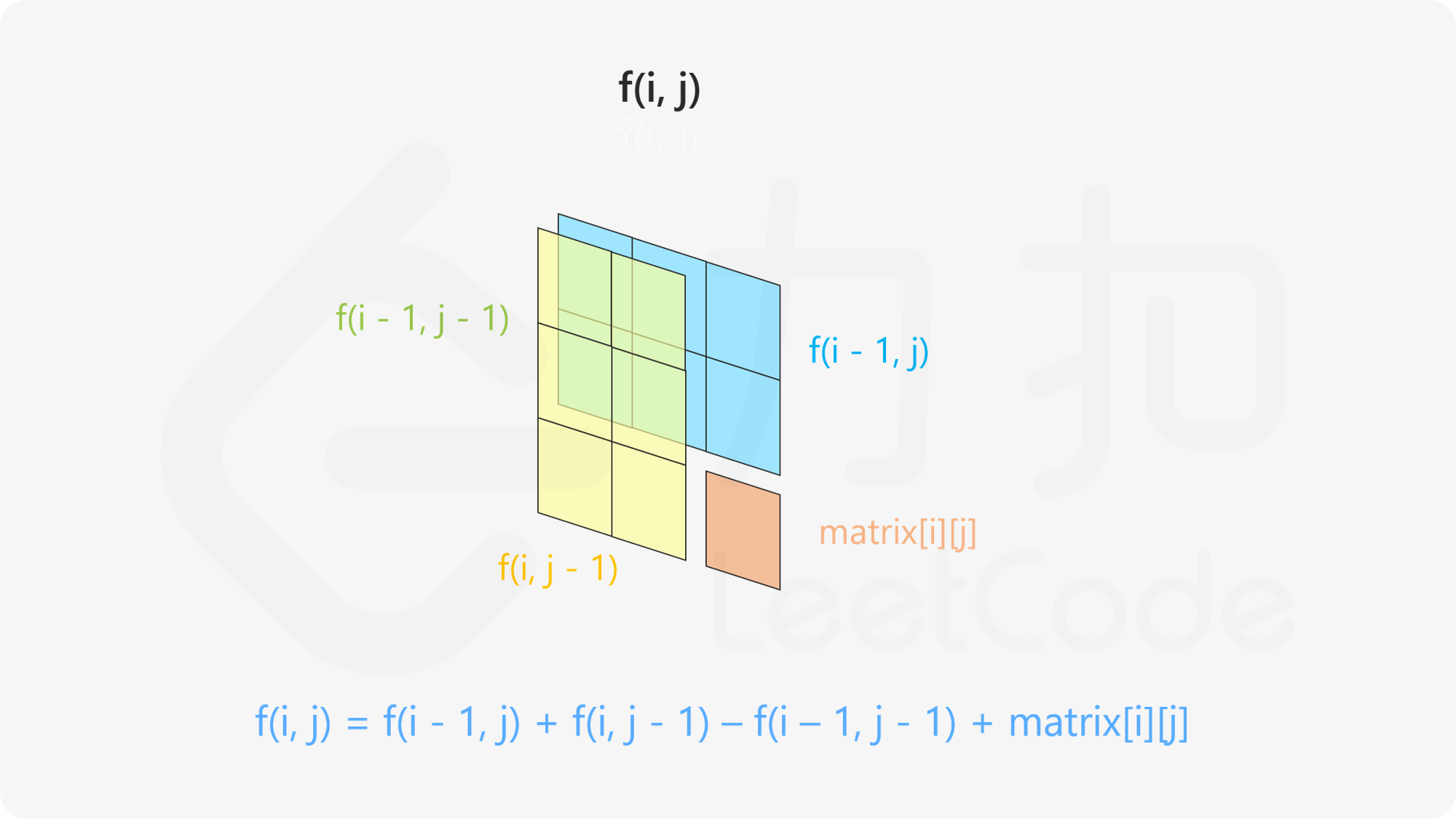
当 $i$ 和 $j$ 都大于 $0$ 时,假设计算 $f(i,j)$ 时已经知道了 $f(i-1,j)$、$f(i,j-1)$ 和 $f(i-1,j-1)$ 的值。为了计算 $f(i,j)$,自然而然会想到使用 $f(i-1,j)$、$f(i,j-1)$ 和 matrix}[i][j]$ 的值。
注意到 $f(i-1,j)$ 和 $f(i,j-1)$ 这两项涉及到的矩阵 matrix 的元素有重合,矩阵 matrix 的以 $(i-1,j-1)$ 为右下角的子矩阵都在这两项中出现。因此如果计算 $f(i-1,j)+f(i,j-1)+\textit{matrix}[i][j]$,则该结果值比 $f(i,j)$ 多了 $f(i-1,j-1)$,因此 $f(i,j)$ 的计算如下:
$$
具体推导如下:
$$
因此在初始化的时候,即可对所有 $0 \le i<m$ 和 $0 \le j<n$ 计算得到 $f(i,j)$ 的值。
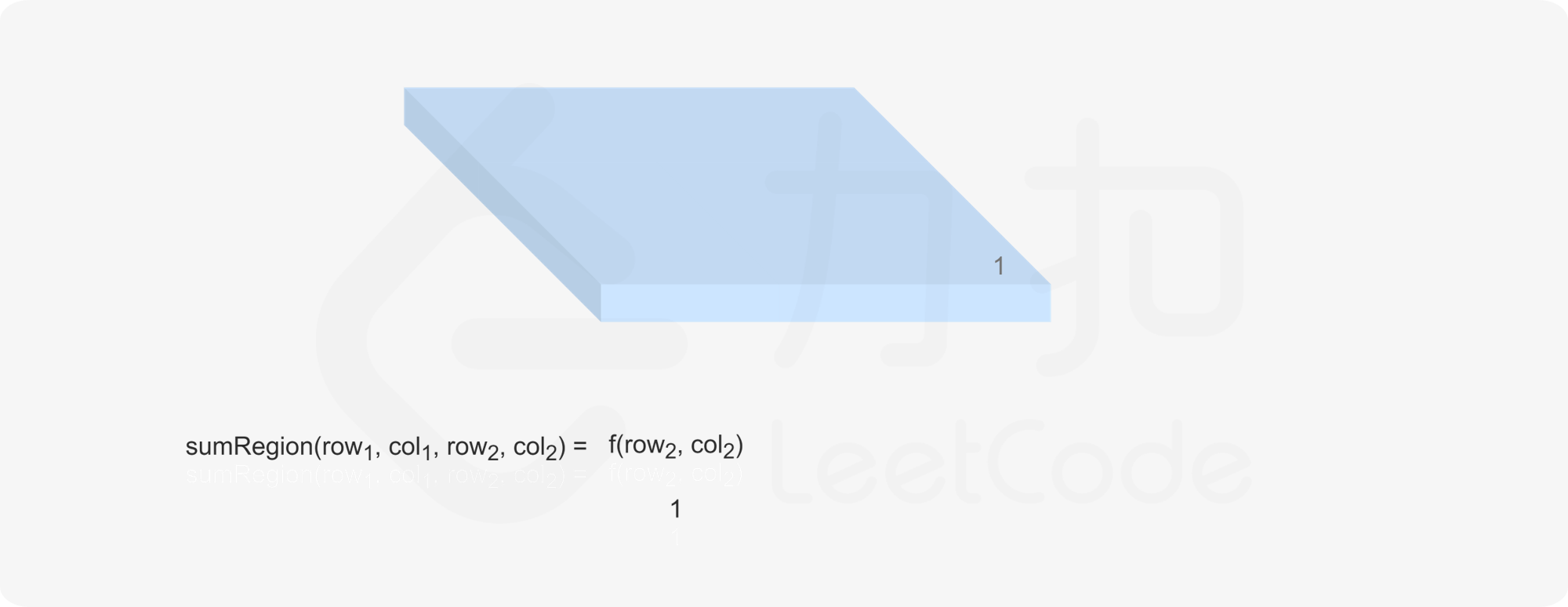
检索时,应利用预处理得到的 $f$ 的值。当 row}_1=0$ 且 col}_1=0$ 时,sumRegion}(\textit{row}_1,\textit{col}_1,\textit{row}_2,\textit{col}_2)=f(\textit{row}_2,\textit{col}_2)$。
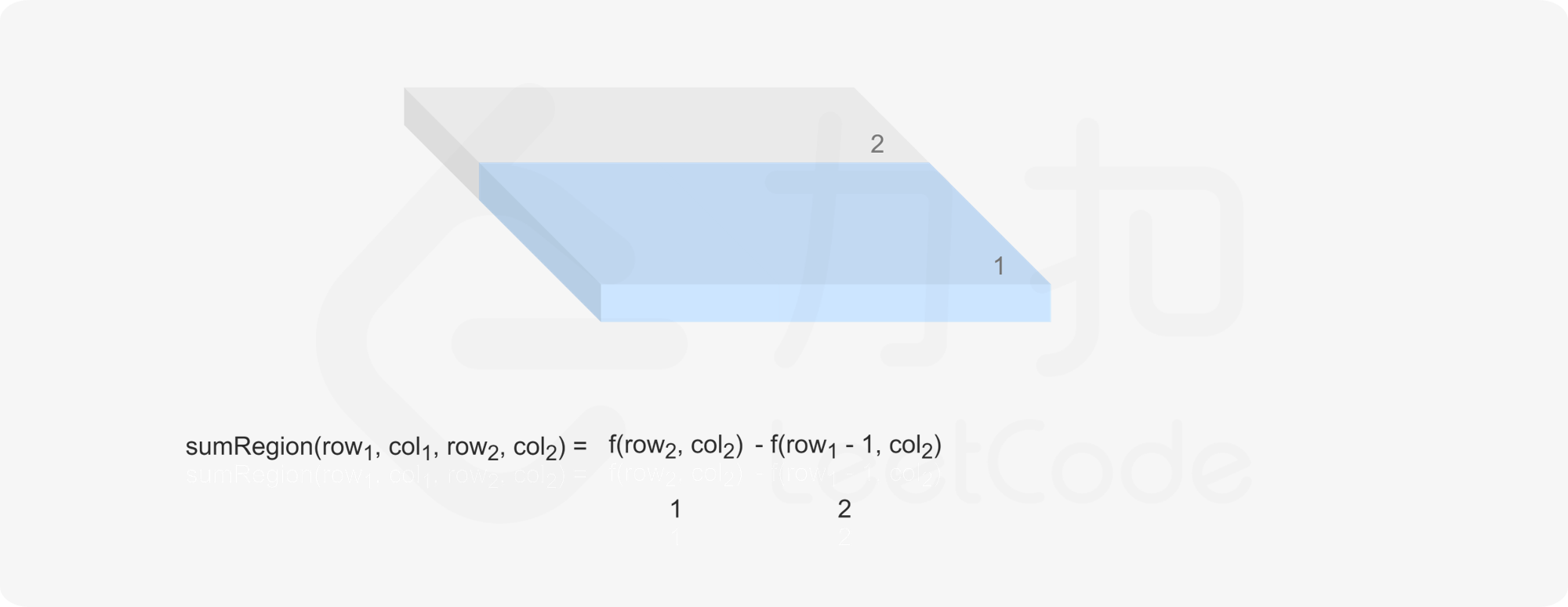
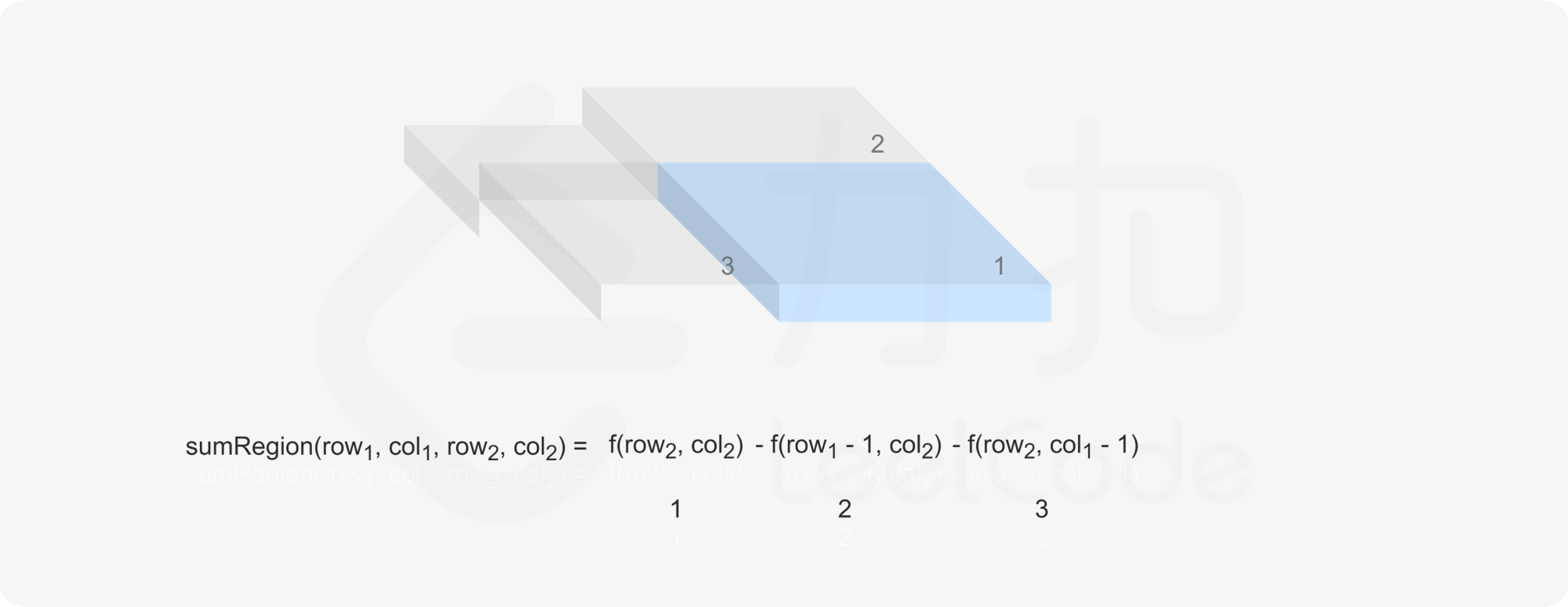
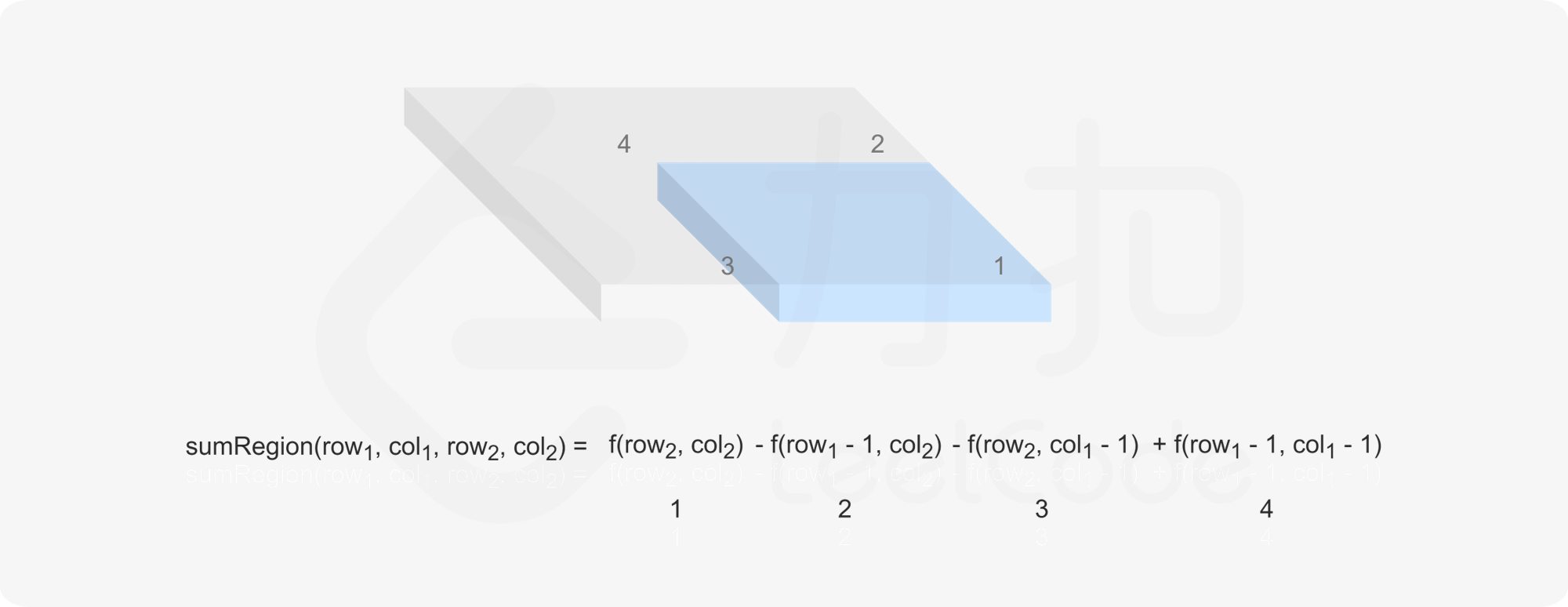
当 row}_1 \le \textit{row}_2$ 且 col}_1 \le \textit{col}_2$ 时,sumRegion}(\textit{row}_1,\textit{col}_1,\textit{row}_2,\textit{col}_2)$ 可以写成如下形式:
$$
<
即可在 $O(1)$ 时间内得到 sumRegion}(\textit{row}_1,\textit{col}_1,\textit{row}_2,\textit{col}_2)$ 的值。
具体实现方面,创建 $m+1$ 行 $n+1$ 列的二维数组 sums,其中 sums}[i+1][j+1]$ 的值为上述 $f(i,j)$ 的值。
将 sums 的行数和列数分别设为 $m+1$ 和 $n+1$ 的目的是为了方便计算 sumRegion}(\textit{row}_1,\textit{col}_1,\textit{row}_2,\textit{col}_2)$ ,不需要对 row}_1=0$ 和 col}_1=0$ 的情况特殊处理。此时有:
$$
[sol2-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class NumMatrix { int [][] sums; public NumMatrix (int [][] matrix) { int m = matrix.length; if (m > 0 ) { int n = matrix[0 ].length; sums = new int [m + 1 ][n + 1 ]; for (int i = 0 ; i < m; i++) { for (int j = 0 ; j < n; j++) { sums[i + 1 ][j + 1 ] = sums[i][j + 1 ] + sums[i + 1 ][j] - sums[i][j] + matrix[i][j]; } } } } public int sumRegion (int row1, int col1, int row2, int col2) { return sums[row2 + 1 ][col2 + 1 ] - sums[row1][col2 + 1 ] - sums[row2 + 1 ][col1] + sums[row1][col1]; } }
[sol2-JavaScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 var NumMatrix = function (matrix ) { const m = matrix.length ; if (m > 0 ) { const n = matrix[0 ].length ; this .sums = new Array (m + 1 ).fill (0 ).map (() => new Array (n + 1 ).fill (0 )); for (let i = 0 ; i < m; i++) { for (let j = 0 ; j < n; j++) { this .sums [i + 1 ][j + 1 ] = this .sums [i][j + 1 ] + this .sums [i + 1 ][j] - this .sums [i][j] + matrix[i][j]; } } } }; NumMatrix .prototype sumRegion = function (row1, col1, row2, col2 ) { return this .sums [row2 + 1 ][col2 + 1 ] - this .sums [row1][col2 + 1 ] - this .sums [row2 + 1 ][col1] + this .sums [row1][col1]; };
[sol2-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 type NumMatrix struct { sums [][]int } func Constructor (matrix [][]int ) m := len (matrix) if m == 0 { return NumMatrix{} } n := len (matrix[0 ]) sums := make ([][]int , m+1 ) sums[0 ] = make ([]int , n+1 ) for i, row := range matrix { sums[i+1 ] = make ([]int , n+1 ) for j, v := range row { sums[i+1 ][j+1 ] = sums[i+1 ][j] + sums[i][j+1 ] - sums[i][j] + v } } return NumMatrix{sums} } func (nm *NumMatrix) int ) int { return nm.sums[row2+1 ][col2+1 ] - nm.sums[row1][col2+1 ] - nm.sums[row2+1 ][col1] + nm.sums[row1][col1] }
[sol2-Python3] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class NumMatrix : def __init__ (self, matrix: List [List [int ]] ): m, n = len (matrix), (len (matrix[0 ]) if matrix else 0 ) self.sums = [[0 ] * (n + 1 ) for _ in range (m + 1 )] _sums = self.sums for i in range (m): for j in range (n): _sums[i + 1 ][j + 1 ] = _sums[i][j + 1 ] + _sums[i + 1 ][j] - _sums[i][j] + matrix[i][j] def sumRegion (self, row1: int , col1: int , row2: int , col2: int ) -> int : _sums = self.sums return _sums[row2 + 1 ][col2 + 1 ] - _sums[row1][col2 + 1 ] - _sums[row2 + 1 ][col1] + _sums[row1][col1]
[sol2-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class NumMatrix {public : vector<vector<int >> sums; NumMatrix (vector<vector<int >>& matrix) { int m = matrix.size (); if (m > 0 ) { int n = matrix[0 ].size (); sums.resize (m + 1 , vector <int >(n + 1 )); for (int i = 0 ; i < m; i++) { for (int j = 0 ; j < n; j++) { sums[i + 1 ][j + 1 ] = sums[i][j + 1 ] + sums[i + 1 ][j] - sums[i][j] + matrix[i][j]; } } } } int sumRegion (int row1, int col1, int row2, int col2) return sums[row2 + 1 ][col2 + 1 ] - sums[row1][col2 + 1 ] - sums[row2 + 1 ][col1] + sums[row1][col1]; } };
[sol2-C] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 typedef struct { int ** sums; int sumsSize; } NumMatrix; NumMatrix* numMatrixCreate (int ** matrix, int matrixSize, int * matrixColSize) { NumMatrix* ret = malloc (sizeof (NumMatrix)); ret->sums = malloc (sizeof (int *) * (matrixSize + 1 )); ret->sumsSize = matrixSize + 1 ; int n = matrixSize ? matrixColSize[0 ] : 0 ; for (int i = 0 ; i <= matrixSize; i++) { ret->sums[i] = malloc (sizeof (int ) * (n + 1 )); memset (ret->sums[i], 0 , sizeof (int ) * (n + 1 )); } for (int i = 0 ; i < matrixSize; i++) { for (int j = 0 ; j < matrixColSize[i]; j++) { ret->sums[i + 1 ][j + 1 ] = ret->sums[i][j + 1 ] + ret->sums[i + 1 ][j] - ret->sums[i][j] + matrix[i][j]; } } return ret; } int numMatrixSumRegion (NumMatrix* obj, int row1, int col1, int row2, int col2) { return obj->sums[row2 + 1 ][col2 + 1 ] - obj->sums[row1][col2 + 1 ] - obj->sums[row2 + 1 ][col1] + obj->sums[row1][col1]; } void numMatrixFree (NumMatrix* obj) { for (int i = 0 ; i < obj->sumsSize; i++) { free (obj->sums[i]); } free (obj->sums); }
复杂度分析
时间复杂度:初始化 $O(mn)$,每次检索 $O(1)$,其中 $m$ 和 $n$ 分别是矩阵 matrix 的行数和列数。
空间复杂度:$O(mn)$,其中 $m$ 和 $n$ 分别是矩阵 matrix 的行数和列数。需要创建一个 $m+1$ 行 $n+1$ 列的二维前缀和数组 sums。
 ,
, ,
, ,
, >
>