树是一个无向图,其中任何两个顶点只通过一条路径连接。 换句话说,一个任何没有简单环路的连通图都是一棵树。
给你一棵包含 n 个节点的树,标记为 0 到 n - 1 。给定数字 n 和一个有 n - 1 条无向边的 edgesedges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条无向边。
可选择树中任何一个节点作为根。当选择节点 x 作为根节点时,设结果树的高度为 h 。在所有可能的树中,具有最小高度的树(即,min(h))被称为最小高度树 。
请你找到所有的 最小高度树 并按 任意顺序 返回它们的根节点标签列表。
树的 高度 是指根节点和叶子节点之间最长向下路径上边的数量。
示例 1:
**输入:** n = 4, edges = [[1,0],[1,2],[1,3]]
**输出:** [1]
**解释:** 如图所示,当根是标签为 1 的节点时,树的高度是 1 ,这是唯一的最小高度树。
示例 2:
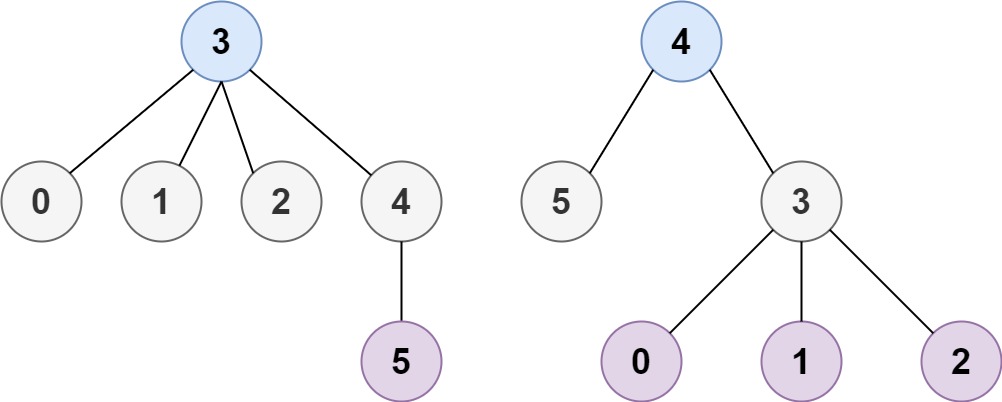
**输入:** n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
**输出:** [3,4]
提示:
1 <= n <= 2 * 104edges.length == n - 10 <= ai, bi < nai != bi所有 (ai, bi) 互不相同
给定的输入 保证 是一棵树,并且 不会有重复的边
方法一:广度优先搜索 思路与算法
题目中给定的含有 $n$ 个节点的树,可以推出含有以下特征:
任意两个节点之间有且仅有一条路径;
树中的共有 $n-1$ 条不同的边;
叶子节点的度为 $1$,非叶子节点的度至少为 $2$;
树的高度由根节点到叶子节点的最大距离决定。
最直接的解法是,枚举以每个节点为根构成的树,然后求出该树的高度,所有树的最小高度即为答案,需要的时间复杂度为 $O(n^2)$,在此不再描述。
设 dist}[x][y]$ 表示从节点 $x$ 到节点 $y$ 的距离,假设树中距离最长的两个节点为 $(x,y)$,它们之间的距离为 maxdist} = \textit{dist}[x][y]$,则可以推出以任意节点构成的树最小高度一定为 minheight} = \Big \lceil \dfrac{\textit{maxdist}}{2} \Big \rceil$,且最小高度的树根节点一定在 节点 $x$ 到节点 $y$ 的路径上。
首先证明树的高度一定为 minheight} = \Big \lceil \dfrac{\textit{maxdist}}{2} \Big \rceil$,可以用反证法证明,假设存在节点 $z$,以节点 $z$ 为根的树的高度 $h < \textit{minheight,则可以推出:
如果节点 $z$ 存在于从 $x$ 到 $y$ 的路径上,由于 $x$ 与 $y$ 均为叶子节点,则可以知道 $x$ 到 $z$ 距离与 $y$ 到 $z$ 距离均小于 minheight,dist}[x][y] = \textit{dist}[x][z] + \textit{dist}[z][y] \le 2 \times \Big \lceil \dfrac{\textit{dist}[x][y]}{2} \Big \rceil - 2 < \textit{dist}[x][y]$,这与 $x$ 到 $y$ 的距离为 dist}[x][y]$ 相矛盾;
如果节点 $z$ 不存在于 $x$ 到 $y$ 的路径上,假设 $z$ 到 $x$ 的路径为 $z \rightarrow \cdots \rightarrow a \rightarrow \cdots \rightarrow x$,$z$ 到 $y$ 的路径为 $z \rightarrow \cdots \rightarrow a \rightarrow \cdots \rightarrow y$,这两个路径之间一定存在公共的交叉点,假设交叉点为 $a$,则可以知道此时 $z$ 到 $x$ 的距离为 dist}[z][x] = \textit{dist}[z][a] + \textit{dist}[a][x]$,$z$ 到 $y$ 的距离为 dist}[z][y] = \textit{dist}[z][a] + \textit{dist}[a][y]$,由于树的高度小于 $h < \textit{minheight,所以可以推出 dist}[z][a] + \textit{dist}[a][x] < \textit{minheight,dist}[z][a] + \textit{dist}[a][y] < \textit{minheight,即可以推出 dist}[a][x] + \textit{dist}[a][y] \le 2 \times \textit{minheight} - 2 = 2 \times \Big \lceil \dfrac{\textit{dist}[x][y]}{2} \Big \rceil - 2 < \textit{dist}[x][y]$,这与 $x$ 到 $y$ 的距离为 dist}[x][y]$ 相矛盾;
其次证明最小高度树的根节点一定存在于 $x$ 到 $y$ 的路径上,假设存在节点 $z$ 它的最小高度为 minheight,但节点 $z$ 不存在于 $x$ 到 $y$ 之间的路径上:
设 $z$ 到 $x$ 的路径为 $z \rightarrow \cdots \rightarrow a \rightarrow \cdots \rightarrow x$,$z$ 到 $y$ 的路径为 $z \rightarrow \cdots \rightarrow a \rightarrow \cdots \rightarrow y$,这两个路径之间一定存在公共的交叉点,假设交叉点为 $a$, 则可以知道此时 $z$ 到 $x$ 的距离为 dist}[z][x] = \textit{dist}[z][a] + \textit{dist}[a][x]$,$z$ 到 $y$ 的距离为 dist}[z][y] = \textit{dist}[z][a] + \textit{dist}[a][y]$,由于树的高度小 $h = \textit{minheight,所以可以推出 dist}[z][a] + \textit{dist}[a][x] \le \textit{minheight,dist}[z][a] + \textit{dist}[a][y] \le \textit{minheight,由于 $z$ 不在 $x$ 到 $y$ 的路径上,所以可以知道 dist}[z][a] \ge 1$,即可以推出 dist}[a][x] < \textit{minheight},\textit{dist}[a][y] < \textit{minheight,即可以推出 dist}[a][x] + \textit{dist}[a][y] \le 2 \times \textit{minheight} - 2 = 2 \times \Big \lceil \dfrac{\textit{dist}[x][y]}{2} \Big \rceil - 2 < \textit{dist}[x][y]$,这与 $x$ 到 $y$ 的距离为 dist}[x][y]$ 相矛盾。
综合上述推理,设两个叶子节点的最长距离为 maxdist,可以得到结论最小高度树的高度为 $\Big \lceil \dfrac{\textit{maxdist}}{2} \Big \rceil$,且最小高度树的根节点一定存在其最长路径上。假设最长的路径的 $m$ 个节点依次为 $p_1 \rightarrow p_2 \rightarrow \cdots \rightarrow p_m$,最长路径的长度为 $m-1$,可以得到以下结论:
因此我们只需要求出路径最长的两个叶子节点即可,并求出其路径的最中间的节点即为最小高度树的根节点。可以利用以下算法找到图中距离最远的两个节点与它们之间的路径:
以任意节点 $p$ 出现,利用广度优先搜索或者深度优先搜索找到以 $p$ 为起点的最长路径的终点 $x$;
以节点 $x$ 出发,找到以 $x$ 为起点的最长路径的终点 $y$;
$x$ 到 $y$ 之间的路径即为图中的最长路径,找到路径的中间节点即为根节点。
上述算法的证明可以参考「算法导论习题解答 9-1 」。在此我们利用广度优先搜索来找到节点的最长路径,首先找到距离节点 $0$ 的最远节点 $x$,然后找到距离节点 $x$ 的最远节点 $y$,然后找到节点 $x$ 与节点 $y$ 的路径,然后找到根节点。
代码
[sol1-Python3] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class Solution : def findMinHeightTrees (self, n: int , edges: List [List [int ]] ) -> List [int ]: if n == 1 : return [0 ] g = [[] for _ in range (n)] for x, y in edges: g[x].append(y) g[y].append(x) parents = [0 ] * n def bfs (start: int ): vis = [False ] * n vis[start] = True q = deque([start]) while q: x = q.popleft() for y in g[x]: if not vis[y]: vis[y] = True parents[y] = x q.append(y) return x x = bfs(0 ) y = bfs(x) path = [] parents[x] = -1 while y != -1 : path.append(y) y = parents[y] m = len (path) return [path[m // 2 ]] if m % 2 else [path[m // 2 - 1 ], path[m // 2 ]]
[sol1-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 class Solution {public : int findLongestNode (int u, vector<int > & parent, vector<vector<int >>& adj) int n = adj.size (); queue<int > qu; vector<bool > visit (n) ; qu.emplace (u); visit[u] = true ; int node = -1 ; while (!qu.empty ()) { int curr = qu.front (); qu.pop (); node = curr; for (auto & v : adj[curr]) { if (!visit[v]) { visit[v] = true ; parent[v] = curr; qu.emplace (v); } } } return node; } vector<int > findMinHeightTrees (int n, vector<vector<int >>& edges) { if (n == 1 ) { return {0 }; } vector<vector<int >> adj (n); for (auto & edge : edges) { adj[edge[0 ]].emplace_back (edge[1 ]); adj[edge[1 ]].emplace_back (edge[0 ]); } vector<int > parent (n, -1 ) ; int x = findLongestNode (0 , parent, adj); int y = findLongestNode (x, parent, adj); vector<int > path; parent[x] = -1 ; while (y != -1 ) { path.emplace_back (y); y = parent[y]; } int m = path.size (); if (m % 2 == 0 ) { return {path[m / 2 - 1 ], path[m / 2 ]}; } else { return {path[m / 2 ]}; } } };
[sol1-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 class Solution { public List<Integer> findMinHeightTrees (int n, int [][] edges) { List<Integer> ans = new ArrayList <Integer>(); if (n == 1 ) { ans.add(0 ); return ans; } List<Integer>[] adj = new List [n]; for (int i = 0 ; i < n; i++) { adj[i] = new ArrayList <Integer>(); } for (int [] edge : edges) { adj[edge[0 ]].add(edge[1 ]); adj[edge[1 ]].add(edge[0 ]); } int [] parent = new int [n]; Arrays.fill(parent, -1 ); int x = findLongestNode(0 , parent, adj); int y = findLongestNode(x, parent, adj); List<Integer> path = new ArrayList <Integer>(); parent[x] = -1 ; while (y != -1 ) { path.add(y); y = parent[y]; } int m = path.size(); if (m % 2 == 0 ) { ans.add(path.get(m / 2 - 1 )); } ans.add(path.get(m / 2 )); return ans; } public int findLongestNode (int u, int [] parent, List<Integer>[] adj) { int n = adj.length; Queue<Integer> queue = new ArrayDeque <Integer>(); boolean [] visit = new boolean [n]; queue.offer(u); visit[u] = true ; int node = -1 ; while (!queue.isEmpty()) { int curr = queue.poll(); node = curr; for (int v : adj[curr]) { if (!visit[v]) { visit[v] = true ; parent[v] = curr; queue.offer(v); } } } return node; } }
[sol1-C#] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 public class Solution { public IList<int > FindMinHeightTrees (int n, int [][] edges IList<int > ans = new List<int >(); if (n == 1 ) { ans.Add(0 ); return ans; } IList<int >[] adj = new IList<int >[n]; for (int i = 0 ; i < n; i++) { adj[i] = new List<int >(); } foreach (int [] edge in edges) { adj[edge[0 ]].Add(edge[1 ]); adj[edge[1 ]].Add(edge[0 ]); } int [] parent = new int [n]; Array.Fill(parent, -1 ); int x = FindLongestNode(0 , parent, adj); int y = FindLongestNode(x, parent, adj); IList<int > path = new List<int >(); parent[x] = -1 ; while (y != -1 ) { path.Add(y); y = parent[y]; } int m = path.Count; if (m % 2 == 0 ) { ans.Add(path[m / 2 - 1 ]); } ans.Add(path[m / 2 ]); return ans; } public int FindLongestNode (int u, int [] parent, IList<int >[] adj int n = adj.Length; Queue<int > queue = new Queue<int >(); bool [] visit = new bool [n]; queue.Enqueue(u); visit[u] = true ; int node = -1 ; while (queue.Count > 0 ) { int curr = queue.Dequeue(); node = curr; foreach (int v in adj[curr]) { if (!visit[v]) { visit[v] = true ; parent[v] = curr; queue.Enqueue(v); } } } return node; } }
[sol1-C] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 int findLongestNode (int u, int * parent, const struct ListNode ** adj, int n) { int * queue = (int *)malloc (sizeof (int ) * n); int head = 0 , tail = 0 ; bool * visit = (bool *)malloc (sizeof (bool ) * n); memset (visit, 0 , sizeof (bool ) * n); queue [tail++] = u; visit[u] = true ; int res = -1 ; while (head != tail) { int curr = queue [head++]; res = curr; struct ListNode * node = while (node) { if (!visit[node->val]) { visit[node->val] = true ; parent[node->val] = curr; queue [tail++] = node->val; } node = node->next; } } free (queue ); free (visit); return res; } int * findMinHeightTrees (int n, int ** edges, int edgesSize, int * edgesColSize, int * returnSize) { int * res = NULL ; if (n == 1 ) { res = (int *)malloc (sizeof (int )); *res = 0 ; *returnSize = 1 ; return res; } struct ListNode ** adj =struct ListNode *)malloc (sizeof (struct ListNode *) * n); for (int i = 0 ; i < n; i++) { adj[i] = NULL ; } for (int i = 0 ; i < edgesSize; i++) { int u = edges[i][0 ]; int v = edges[i][1 ]; struct ListNode * node =struct ListNode *)malloc (sizeof (struct ListNode)); node->val = u; node->next = adj[v]; adj[v] = node; node = (struct ListNode *)malloc (sizeof (struct ListNode)); node->val = v; node->next = adj[u]; adj[u] = node; } int * parent = (int *)malloc (sizeof (int ) * n); int x = findLongestNode(0 , parent, adj, n); int y = findLongestNode(x, parent, adj, n); int * path = (int *)malloc (sizeof (int ) * n); int pos = 0 ; parent[x] = -1 ; while (y != -1 ) { path[pos++] = y; y = parent[y]; } if (pos % 2 == 0 ) { res = (int *)malloc (sizeof (int ) * 2 ); res[0 ] = path[pos / 2 - 1 ]; res[1 ] = path[pos / 2 ]; *returnSize = 2 ; } else { res = (int *)malloc (sizeof (int )); *res = path[pos / 2 ]; *returnSize = 1 ; } free (path); free (parent); for (int i = 0 ; i < n; i++) { struct ListNode * node = while (node) { struct ListNode * curr = node = curr->next; free (curr); } } free (adj); return res; }
[sol1-JavaScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 var findMinHeightTrees = function (n, edges ) { const ans = []; if (n === 1 ) { ans.push (0 ); return ans; } const adj = new Array (n).fill (0 ).map (() => new Array ()); for (const edge of edges) { adj[edge[0 ]].push (edge[1 ]); adj[edge[1 ]].push (edge[0 ]); } const parent = new Array (n).fill (-1 ); const x = findLongestNode (0 , parent, adj); let y = findLongestNode (x, parent, adj); const path = []; parent[x] = -1 ; while (y !== -1 ) { path.push (y); y = parent[y]; } const m = path.length ; if (m % 2 === 0 ) { ans.push (path[Math .floor (m / 2 ) - 1 ]); } ans.push (path[Math .floor (m / 2 )]); return ans; } const findLongestNode = (u, parent, adj ) => { const n = adj.length ; const queue = []; const visit = new Array (n).fill (false ); queue.push (u); visit[u] = true ; let node = -1 ; while (queue.length ) { const curr = queue.shift (); node = curr; for (const v of adj[curr]) { if (!visit[v]) { visit[v] = true ; parent[v] = curr; queue.push (v); } } } return node; };
[sol1-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 func findMinHeightTrees (n int , edges [][]int ) int { if n == 1 { return []int {0 } } g := make ([][]int , n) for _, e := range edges { x, y := e[0 ], e[1 ] g[x] = append (g[x], y) g[y] = append (g[y], x) } parents := make ([]int , n) bfs := func (start int ) int ) { vis := make ([]bool , n) vis[start] = true q := []int {start} for len (q) > 0 { x, q = q[0 ], q[1 :] for _, y := range g[x] { if !vis[y] { vis[y] = true parents[y] = x q = append (q, y) } } } return } x := bfs(0 ) y := bfs(x) path := []int {} parents[x] = -1 for y != -1 { path = append (path, y) y = parents[y] } m := len (path) if m%2 == 0 { return []int {path[m/2 -1 ], path[m/2 ]} } return []int {path[m/2 ]} }
复杂度分析
时间复杂度:$O(n)$,其中 $n$ 是为节点的个数。图中边的个数为 $n-1$,因此建立图的关系需要的时间复杂度为 $O(n)$,通过广度优先搜索需要的时间复杂度为 $O(n + n - 1)$,求最长路径的时间复杂度为 $O(n)$,因此总的时间复杂度为 $O(n)$。
空间复杂度:$O(n)$,其中 $n$ 是节点的个数。由于题目给定的图中任何两个顶点都只有一条路径连接,因此图中边的数目刚好等于 $n-1$,用邻接表构造图所需的空间刚好为 $O(2 \times n)$,存储每个节点的距离和父节点均为 $O(n)$,使用广度优先搜索时,队列中最多有 $n$ 个元素,所需的空间也为 $O(n)$,因此空间复杂度为 $O(n)$。
方法二:深度优先搜索 思路与算法
方法一中使用广度优先搜索求出路径最长的节点与路径,我们还可以使用深度优先搜索来实现。首先找到距离节点 $0$ 的最远节点 $x$,然后找到距离节点 $x$ 的最远节点 $y$,然后找到节点 $x$ 与节点 $y$ 的路径,然后找到根节点。
代码
[sol2-Python3] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class Solution : def findMinHeightTrees (self, n: int , edges: List [List [int ]] ) -> List [int ]: if n == 1 : return [0 ] g = [[] for _ in range (n)] for x, y in edges: g[x].append(y) g[y].append(x) parents = [0 ] * n maxDepth, node = 0 , -1 def dfs (x: int , pa: int , depth: int ): nonlocal maxDepth, node if depth > maxDepth: maxDepth, node = depth, x parents[x] = pa for y in g[x]: if y != pa: dfs(y, x, depth + 1 ) dfs(0 , -1 , 1 ) maxDepth = 0 dfs(node, -1 , 1 ) path = [] while node != -1 : path.append(node) node = parents[node] m = len (path) return [path[m // 2 ]] if m % 2 else [path[m // 2 - 1 ], path[m // 2 ]]
[sol2-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 class Solution {public : void dfs (int u, vector<int > & dist, vector<int > & parent, const vector<vector<int >> & adj) for (auto & v : adj[u]) { if (dist[v] < 0 ) { dist[v] = dist[u] + 1 ; parent[v] = u; dfs (v, dist, parent, adj); } } } int findLongestNode (int u, vector<int > & parent, const vector<vector<int >> & adj) int n = adj.size (); vector<int > dist (n, -1 ) ; dist[u] = 0 ; dfs (u, dist, parent, adj); int maxdist = 0 ; int node = -1 ; for (int i = 0 ; i < n; i++) { if (dist[i] > maxdist) { maxdist = dist[i]; node = i; } } return node; } vector<int > findMinHeightTrees (int n, vector<vector<int >>& edges) { if (n == 1 ) { return {0 }; } vector<vector<int >> adj (n); for (auto & edge : edges) { adj[edge[0 ]].emplace_back (edge[1 ]); adj[edge[1 ]].emplace_back (edge[0 ]); } vector<int > parent (n, -1 ) ; int x = findLongestNode (0 , parent, adj); int y = findLongestNode (x, parent, adj); vector<int > path; parent[x] = -1 ; while (y != -1 ) { path.emplace_back (y); y = parent[y]; } int m = path.size (); if (m % 2 == 0 ) { return {path[m / 2 - 1 ], path[m / 2 ]}; } else { return {path[m / 2 ]}; } } };
[sol2-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 class Solution { public List<Integer> findMinHeightTrees (int n, int [][] edges) { List<Integer> ans = new ArrayList <Integer>(); if (n == 1 ) { ans.add(0 ); return ans; } List<Integer>[] adj = new List [n]; for (int i = 0 ; i < n; i++) { adj[i] = new ArrayList <Integer>(); } for (int [] edge : edges) { adj[edge[0 ]].add(edge[1 ]); adj[edge[1 ]].add(edge[0 ]); } int [] parent = new int [n]; Arrays.fill(parent, -1 ); int x = findLongestNode(0 , parent, adj); int y = findLongestNode(x, parent, adj); List<Integer> path = new ArrayList <Integer>(); parent[x] = -1 ; while (y != -1 ) { path.add(y); y = parent[y]; } int m = path.size(); if (m % 2 == 0 ) { ans.add(path.get(m / 2 - 1 )); } ans.add(path.get(m / 2 )); return ans; } public int findLongestNode (int u, int [] parent, List<Integer>[] adj) { int n = adj.length; int [] dist = new int [n]; Arrays.fill(dist, -1 ); dist[u] = 0 ; dfs(u, dist, parent, adj); int maxdist = 0 ; int node = -1 ; for (int i = 0 ; i < n; i++) { if (dist[i] > maxdist) { maxdist = dist[i]; node = i; } } return node; } public void dfs (int u, int [] dist, int [] parent, List<Integer>[] adj) { for (int v : adj[u]) { if (dist[v] < 0 ) { dist[v] = dist[u] + 1 ; parent[v] = u; dfs(v, dist, parent, adj); } } } }
[sol2-C#] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 public class Solution { public IList<int > FindMinHeightTrees (int n, int [][] edges IList<int > ans = new List<int >(); if (n == 1 ) { ans.Add(0 ); return ans; } IList<int >[] adj = new IList<int >[n]; for (int i = 0 ; i < n; i++) { adj[i] = new List<int >(); } foreach (int [] edge in edges) { adj[edge[0 ]].Add(edge[1 ]); adj[edge[1 ]].Add(edge[0 ]); } int [] parent = new int [n]; Array.Fill(parent, -1 ); int x = FindLongestNode(0 , parent, adj); int y = FindLongestNode(x, parent, adj); IList<int > path = new List<int >(); parent[x] = -1 ; while (y != -1 ) { path.Add(y); y = parent[y]; } int m = path.Count; if (m % 2 == 0 ) { ans.Add(path[m / 2 - 1 ]); } ans.Add(path[m / 2 ]); return ans; } public int FindLongestNode (int u, int [] parent, IList<int >[] adj int n = adj.Length; int [] dist = new int [n]; Array.Fill(dist, -1 ); dist[u] = 0 ; DFS(u, dist, parent, adj); int maxdist = 0 ; int node = -1 ; for (int i = 0 ; i < n; i++) { if (dist[i] > maxdist) { maxdist = dist[i]; node = i; } } return node; } public void DFS (int u, int [] dist, int [] parent, IList<int >[] adj foreach (int v in adj[u]) { if (dist[v] < 0 ) { dist[v] = dist[u] + 1 ; parent[v] = u; DFS(v, dist, parent, adj); } } } }
[sol2-C] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 void dfs (int u, int * dist, int * parent, const struct ListNode ** adj) { for (struct ListNode * node = adj[u]; node; node = node->next) { int v = node->val; if (dist[v] < 0 ) { dist[v] = dist[u] + 1 ; parent[v] = u; dfs(v, dist, parent, adj); } } } int findLongestNode (int u, int * parent, const struct ListNode ** adj, int n) { int * dist = (int *)malloc (sizeof (int ) * n); memset (dist, -1 , sizeof (int ) * n); dist[u] = 0 ; dfs(u, dist, parent, adj); int maxdist = 0 ; int node = -1 ; for (int i = 0 ; i < n; i++) { if (dist[i] > maxdist) { maxdist = dist[i]; node = i; } } free (dist); return node; } int * findMinHeightTrees (int n, int ** edges, int edgesSize, int * edgesColSize, int * returnSize) { int * res = NULL ; if (n == 1 ) { res = (int *)malloc (sizeof (int )); *res = 0 ; *returnSize = 1 ; return res; } struct ListNode ** adj =struct ListNode *)malloc (sizeof (struct ListNode *) * n); for (int i = 0 ; i < n; i++) { adj[i] = NULL ; } for (int i = 0 ; i < edgesSize; i++) { int u = edges[i][0 ]; int v = edges[i][1 ]; struct ListNode * node =struct ListNode *)malloc (sizeof (struct ListNode)); node->val = u; node->next = adj[v]; adj[v] = node; node = (struct ListNode *)malloc (sizeof (struct ListNode)); node->val = v; node->next = adj[u]; adj[u] = node; } int * parent = (int *)malloc (sizeof (int ) * n); int x = findLongestNode(0 , parent, adj, n); int y = findLongestNode(x, parent, adj, n); int * path = (int *)malloc (sizeof (int ) * n); int pos = 0 ; parent[x] = -1 ; while (y != -1 ) { path[pos++] = y; y = parent[y]; } if (pos % 2 == 0 ) { res = (int *)malloc (sizeof (int ) * 2 ); res[0 ] = path[pos / 2 - 1 ]; res[1 ] = path[pos / 2 ]; *returnSize = 2 ; } else { res = (int *)malloc (sizeof (int )); *res = path[pos / 2 ]; *returnSize = 1 ; } free (path); free (parent); for (int i = 0 ; i < n; i++) { struct ListNode * node = while (node) { struct ListNode * curr = node = curr->next; free (curr); } } free (adj); return res; }
[sol2-JavaScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 var findMinHeightTrees = function (n, edges ) { const ans = []; if (n === 1 ) { ans.push (0 ); return ans; } const adj = new Array (n).fill (0 ).map (() => new Array ()); for (const edge of edges) { adj[edge[0 ]].push (edge[1 ]); adj[edge[1 ]].push (edge[0 ]); } const parent = new Array (n).fill (-1 ); let x = findLongestNode (0 , parent, adj); let y = findLongestNode (x, parent, adj); const path = []; parent[x] = -1 ; while (y !== -1 ) { path.push (y); y = parent[y]; } const m = path.length ; if (m % 2 === 0 ) { ans.push (path[Math .floor (m / 2 ) - 1 ]); } ans.push (path[Math .floor (m / 2 )]); return ans; } const findLongestNode = (u, parent, adj ) => { const n = adj.length ; const dist = new Array (n).fill (-1 ); dist[u] = 0 ; const dfs = (u, dist, parent, adj ) => { for (const v of adj[u]) { if (dist[v] < 0 ) { dist[v] = dist[u] + 1 ; parent[v] = u; dfs (v, dist, parent, adj); } } } dfs (u, dist, parent, adj); let maxdist = 0 ; let node = -1 ; for (let i = 0 ; i < n; i++) { if (dist[i] > maxdist) { maxdist = dist[i]; node = i; } } return node; }
[sol2-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 func findMinHeightTrees (n int , edges [][]int ) int { if n == 1 { return []int {0 } } g := make ([][]int , n) for _, e := range edges { x, y := e[0 ], e[1 ] g[x] = append (g[x], y) g[y] = append (g[y], x) } parents := make ([]int , n) maxDepth, node := 0 , -1 var dfs func (int , int , int ) dfs = func (x, pa, depth int ) if depth > maxDepth { maxDepth, node = depth, x } parents[x] = pa for _, y := range g[x] { if y != pa { dfs(y, x, depth+1 ) } } } dfs(0 , -1 , 1 ) maxDepth = 0 dfs(node, -1 , 1 ) path := []int {} for node != -1 { path = append (path, node) node = parents[node] } m := len (path) if m%2 == 0 { return []int {path[m/2 -1 ], path[m/2 ]} } return []int {path[m/2 ]} }
复杂度分析
时间复杂度:$O(n)$,其中 $n$ 是为节点的个数。图中边的个数为 $n-1$,因此建立图的关系需要的时间复杂度为 $O(n)$,通过深度优先搜索需要的时间复杂度为 $O(n + n - 1)$,求最长路径的时间复杂度为 $O(n)$,因此总的时间复杂度为 $O(n)$。
空间复杂度:$O(n)$,其中 $n$ 是节点的个数。由于题目给定的图中任何两个顶点都只有一条路径连接,因此图中边的数目刚好等于 $n-1$,用邻接表构造图所需的空间刚好为 $O(2 \times n)$,存储每个节点的距离和父节点均为 $O(n)$,使用深度优先搜索时,递归的最大深度为 $O(n)$,所需的空间也为 $O(n)$,因此总的空间复杂度为 $O(n)$。
方法三:拓扑排序 思路与算法
由于树的高度由根节点到叶子节点之间的最大距离构成,假设树中距离最长的两个节点为 $(x,y)$,它们之间的距离为 maxdist} = \textit{dist}[x][y]$,假设 $x$ 到 $y$ 的路径为 $x \rightarrow p_1 \rightarrow p_2 \rightarrow \cdots \rightarrow p_{k-1} \rightarrow p_k \rightarrow y$,根据方法一的证明已知最小树的根节点一定为该路径中的中间节点,我们尝试删除最外层的度为 $1$ 的节点 $x,y$ 后,则可以知道路径中与 $x,y$ 相邻的节点 $p_1, p_k$ 此时也变为度为 $1$ 的节点,此时我们再次删除最外层度为 $1$ 的节点直到剩下根节点为止。
可以用反证法证明,删除节点 $x, y$ 之后,节点 $p_1, p_k$ 一定变为度为 $1$ 的叶子节点,假设删除 $x, y$ 之后,节点 $p_1, p_k$ 的度不为 $1$,可以假设 $p_1$ 的度不为 $1$, 则此时与 $p_1$ 相邻的节点除了 $p_2$ 外还有其余节点 $q$ 且 $q$ 不在最长的路径中,此时我们知道在最开始的树中节点 $q$ 的度一定不为 $1$,与 $q$ 连接的节点为 $q’$,则此时经过节点 $q’$ 的路径 dist}[q’][y] = \textit{dist}[p_1][y] + 2 > \textit{dist}[x][y]$,这与 dist}[x][y]$ 为树中的最长路径相矛盾。
实际做法如下:
首先找到所有度为 $1$ 的节点压入队列,此时令节点剩余计数 remainNodes} = n$;
同时将当前 remainNodes 计数减去出度为 $1$ 的节点数目,将最外层的度为 $1$ 的叶子节点取出,并将与之相邻的节点的度减少,重复上述步骤将当前节点中度为 $1$ 的节点压入队列中;
重复上述步骤,直到剩余的节点数组 remainNodes} \le 2$ 时,此时剩余的节点即为当前高度最小树的根节点。
代码
[sol3-Python3] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution : def findMinHeightTrees (self, n: int , edges: List [List [int ]] ) -> List [int ]: if n == 1 : return [0 ] g = [[] for _ in range (n)] deg = [0 ] * n for x, y in edges: g[x].append(y) g[y].append(x) deg[x] += 1 deg[y] += 1 q = [i for i, d in enumerate (deg) if d == 1 ] remainNodes = n while remainNodes > 2 : remainNodes -= len (q) tmp = q q = [] for x in tmp: for y in g[x]: deg[y] -= 1 if deg[y] == 1 : q.append(y) return q
[sol3-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 class Solution {public : vector<int > findMinHeightTrees (int n, vector<vector<int >>& edges) { if (n == 1 ) { return {0 }; } vector<int > degree (n) ; vector<vector<int >> adj (n); for (auto & edge : edges){ adj[edge[0 ]].emplace_back (edge[1 ]); adj[edge[1 ]].emplace_back (edge[0 ]); degree[edge[0 ]]++; degree[edge[1 ]]++; } queue<int > qu; vector<int > ans; for (int i = 0 ; i < n; i++) { if (degree[i] == 1 ) { qu.emplace (i); } } int remainNodes = n; while (remainNodes > 2 ) { int sz = qu.size (); remainNodes -= sz; for (int i = 0 ; i < sz; i++) { int curr = qu.front (); qu.pop (); for (auto & v : adj[curr]) { if (--degree[v] == 1 ) { qu.emplace (v); } } } } while (!qu.empty ()) { ans.emplace_back (qu.front ()); qu.pop (); } return ans; } };
[sol3-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 class Solution { public List<Integer> findMinHeightTrees (int n, int [][] edges) { List<Integer> ans = new ArrayList <Integer>(); if (n == 1 ) { ans.add(0 ); return ans; } int [] degree = new int [n]; List<Integer>[] adj = new List [n]; for (int i = 0 ; i < n; i++) { adj[i] = new ArrayList <Integer>(); } for (int [] edge : edges) { adj[edge[0 ]].add(edge[1 ]); adj[edge[1 ]].add(edge[0 ]); degree[edge[0 ]]++; degree[edge[1 ]]++; } Queue<Integer> queue = new ArrayDeque <Integer>(); for (int i = 0 ; i < n; i++) { if (degree[i] == 1 ) { queue.offer(i); } } int remainNodes = n; while (remainNodes > 2 ) { int sz = queue.size(); remainNodes -= sz; for (int i = 0 ; i < sz; i++) { int curr = queue.poll(); for (int v : adj[curr]) { degree[v]--; if (degree[v] == 1 ) { queue.offer(v); } } } } while (!queue.isEmpty()) { ans.add(queue.poll()); } return ans; } }
[sol3-C#] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 public class Solution { public IList<int > FindMinHeightTrees (int n, int [][] edges IList<int > ans = new List<int >(); if (n == 1 ) { ans.Add(0 ); return ans; } int [] degree = new int [n]; IList<int >[] adj = new IList<int >[n]; for (int i = 0 ; i < n; i++) { adj[i] = new List<int >(); } foreach (int [] edge in edges) { adj[edge[0 ]].Add(edge[1 ]); adj[edge[1 ]].Add(edge[0 ]); degree[edge[0 ]]++; degree[edge[1 ]]++; } Queue<int > queue = new Queue<int >(); for (int i = 0 ; i < n; i++) { if (degree[i] == 1 ) { queue.Enqueue(i); } } int remainNodes = n; while (remainNodes > 2 ) { int sz = queue.Count; remainNodes -= sz; for (int i = 0 ; i < sz; i++) { int curr = queue.Dequeue(); foreach (int v in adj[curr]) { degree[v]--; if (degree[v] == 1 ) { queue.Enqueue(v); } } } } while (queue.Count > 0 ) { ans.Add(queue.Dequeue()); } return ans; } }
[sol3-C] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 int * findMinHeightTrees (int n, int ** edges, int edgesSize, int * edgesColSize, int * returnSize) { int * res = NULL ; if (n == 1 ) { res = (int *)malloc (sizeof (int )); *res = 0 ; *returnSize = 1 ; return res; } struct ListNode ** adj =struct ListNode *)malloc (sizeof (struct ListNode *) * n); int * degree = (int *)malloc (sizeof (int ) * n); memset (degree, 0 , sizeof (int ) * n); for (int i = 0 ; i < n; i++) { adj[i] = NULL ; } for (int i = 0 ; i < edgesSize; i++) { int u = edges[i][0 ]; int v = edges[i][1 ]; struct ListNode * node =struct ListNode *)malloc (sizeof (struct ListNode)); node->val = u; node->next = adj[v]; adj[v] = node; node = (struct ListNode *)malloc (sizeof (struct ListNode)); node->val = v; node->next = adj[u]; adj[u] = node; degree[u]++; degree[v]++; } int * queue = (int *)malloc (sizeof (int ) * n); int head = 0 ; int tail = 0 ; for (int i = 0 ; i < n; i++) { if (degree[i] == 1 ) { queue [tail++] = i; } } int remainNodes = n; while (remainNodes > 2 ) { int sz = tail - head; remainNodes -= sz; for (int i = 0 ; i < sz; i++) { int curr = queue [head++]; struct ListNode * node = while (node) { int v = node->val; degree[v]--; if (degree[v] == 1 ) { queue [tail++] = v; } node = node->next; } } } res = (int *)malloc (sizeof (int ) * remainNodes); *returnSize = remainNodes; int pos = 0 ; while (head != tail) { res[pos++] = queue [head++]; } free (queue ); free (degree); for (int i = 0 ; i < n; i++) { struct ListNode * node = while (node) { struct ListNode * curr = node = curr->next; free (curr); } } free (adj); return res; }
[sol3-JavaScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 var findMinHeightTrees = function (n, edges ) { const ans = []; if (n === 1 ) { ans.push (0 ); return ans; } const degree = new Array (n).fill (0 ); const adj = new Array (n).fill (0 ).map (() => new Array ()); for (const edge of edges) { adj[edge[0 ]].push (edge[1 ]); adj[edge[1 ]].push (edge[0 ]); degree[edge[0 ]]++; degree[edge[1 ]]++; } const queue = []; for (let i = 0 ; i < n; i++) { if (degree[i] === 1 ) { queue.push (i); } } let remainNodes = n; while (remainNodes > 2 ) { const sz = queue.length ; remainNodes -= sz; for (let i = 0 ; i < sz; i++) { const curr = queue.shift (); for (const v of adj[curr]) { degree[v]--; if (degree[v] === 1 ) { queue.push (v); } } } } while (queue.length ) { ans.push (queue.shift ()); } return ans; };
[sol3-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 func findMinHeightTrees (n int , edges [][]int ) int { if n == 1 { return []int {0 } } g := make ([][]int , n) deg := make ([]int , n) for _, e := range edges { x, y := e[0 ], e[1 ] g[x] = append (g[x], y) g[y] = append (g[y], x) deg[x]++ deg[y]++ } q := []int {} for i, d := range deg { if d == 1 { q = append (q, i) } } remainNodes := n for remainNodes > 2 { remainNodes -= len (q) tmp := q q = nil for _, x := range tmp { for _, y := range g[x] { deg[y]-- if deg[y] == 1 { q = append (q, y) } } } } return q }
复杂度分析
时间复杂度:$O(n)$,其中 $n$ 是为节点的个数。图中边的个数为 $n-1$,因此建立图的关系需要的时间复杂度为 $O(n)$,通过广度优先搜索需要的时间复杂度为 $O(n + n - 1)$,求最长路径的时间复杂度为 $O(n)$,因此总的时间复杂度为 $O(n)$。
空间复杂度:$O(n)$,其中 $n$ 是节点的个数。由于题目给定的图中任何两个顶点都只有一条路径连接,因此图中边的数目刚好等于 $n-1$,用邻接表构造图所需的空间刚好为 $O(2 \times n)$,存储每个节点的距离和父节点均为 $O(n)$,使用广度优先搜索时,队列中最多有 $n$ 个元素,所需的空间也为 $O(n)$,因此空间复杂度为 $O(n)$。