超级丑数 是一个正整数,并满足其所有质因数都出现在质数数组 primes 中。
给你一个整数 n 和一个整数数组 primes ,返回第 n 个 超级丑数 。
题目数据保证第 n 个 超级丑数 在 32-bit 带符号整数范围内。
示例 1:
**输入:** n = 12, primes = [2,7,13,19]
**输出:** 32
**解释:** 给定长度为 4 的质数数组 primes = [2,7,13,19],前 12 个超级丑数序列为:[1,2,4,7,8,13,14,16,19,26,28,32] 。
示例 2:
**输入:** n = 1, primes = [2,3,5]
**输出:** 1
**解释:** 1 不含质因数,因此它的所有质因数都在质数数组 primes = [2,3,5] 中。
提示:
1 <= n <= 1051 <= primes.length <= 1002 <= primes[i] <= 1000- 题目数据 保证
primes[i] 是一个质数
primes 中的所有值都 互不相同 ,且按 递增顺序 排列
前言
这道题和「264. 丑数 II 」相似,区别在于,第 264 题规定丑数是只包含质因数 $2$、$3$ 和 $5$ 的正整数,这道题规定超级丑数是只包含数组 primes 中的质因数的正整数。
第 264 题的方法包括最小堆和动态规划。由于这道题的数据规模较大,因此最小堆的解法会超时,此处只提供动态规划的解法。
方法一:动态规划
定义数组 dp,其中 dp}[i]$ 表示第 $i$ 个超级丑数,第 $n$ 个超级丑数即为 dp}[n]$。
由于最小的超级丑数是 $1$,因此 dp}[1]=1$。
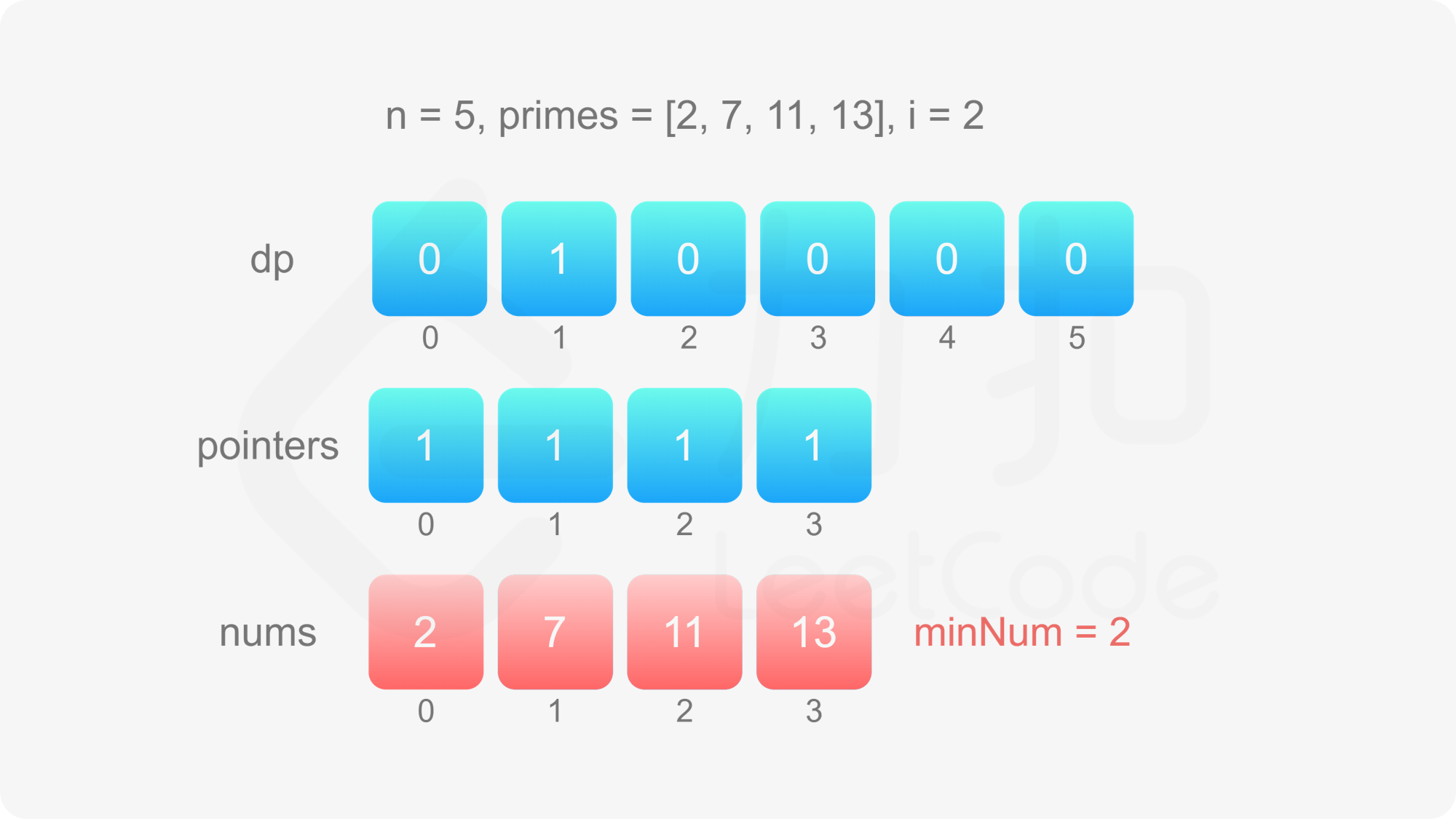
如何得到其余的超级丑数呢?创建与数组 primes 相同长度的数组 pointers,表示下一个超级丑数是当前指针指向的超级丑数乘以对应的质因数。初始时,数组 pointers 的元素值都是 $1$。
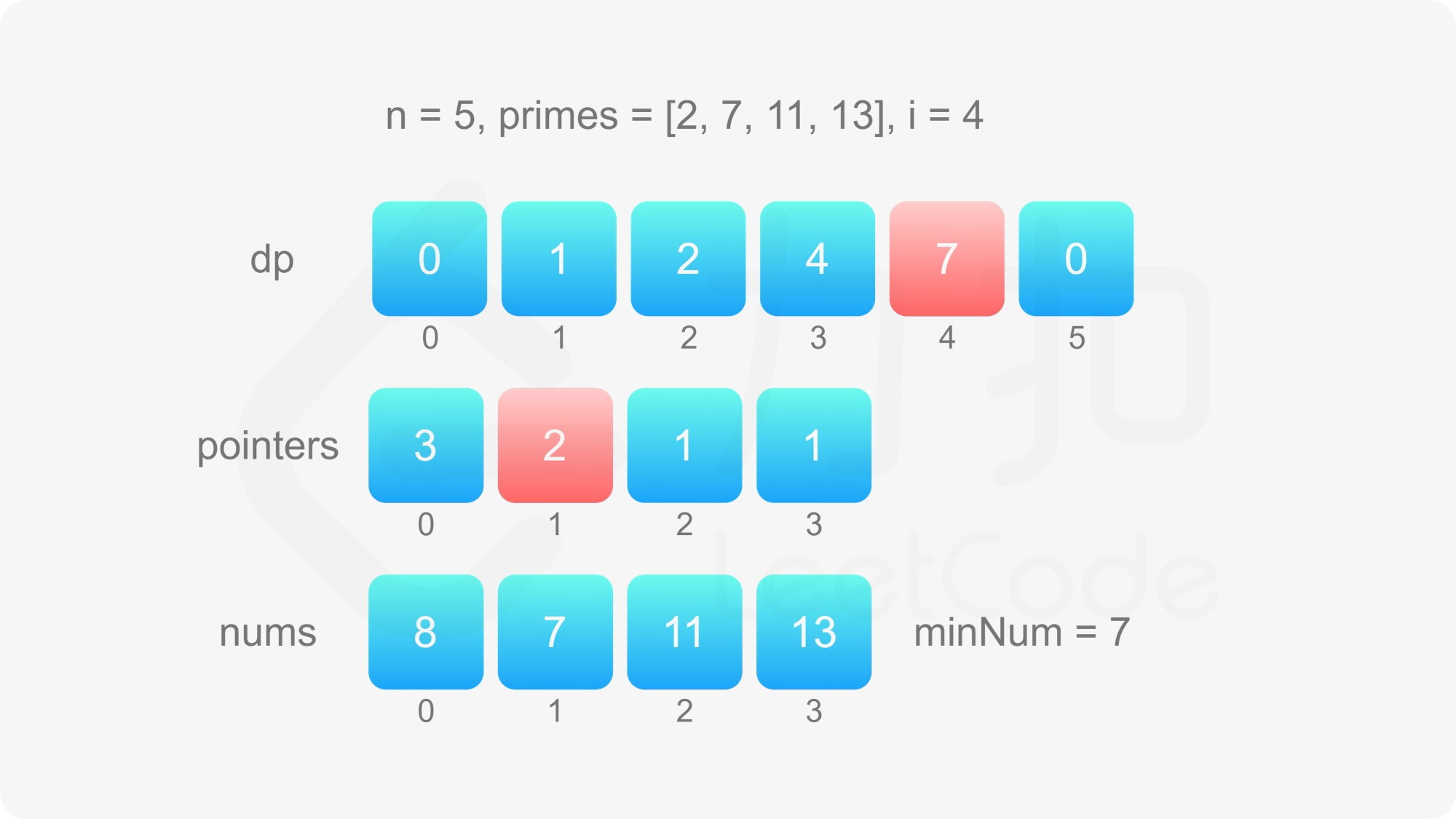
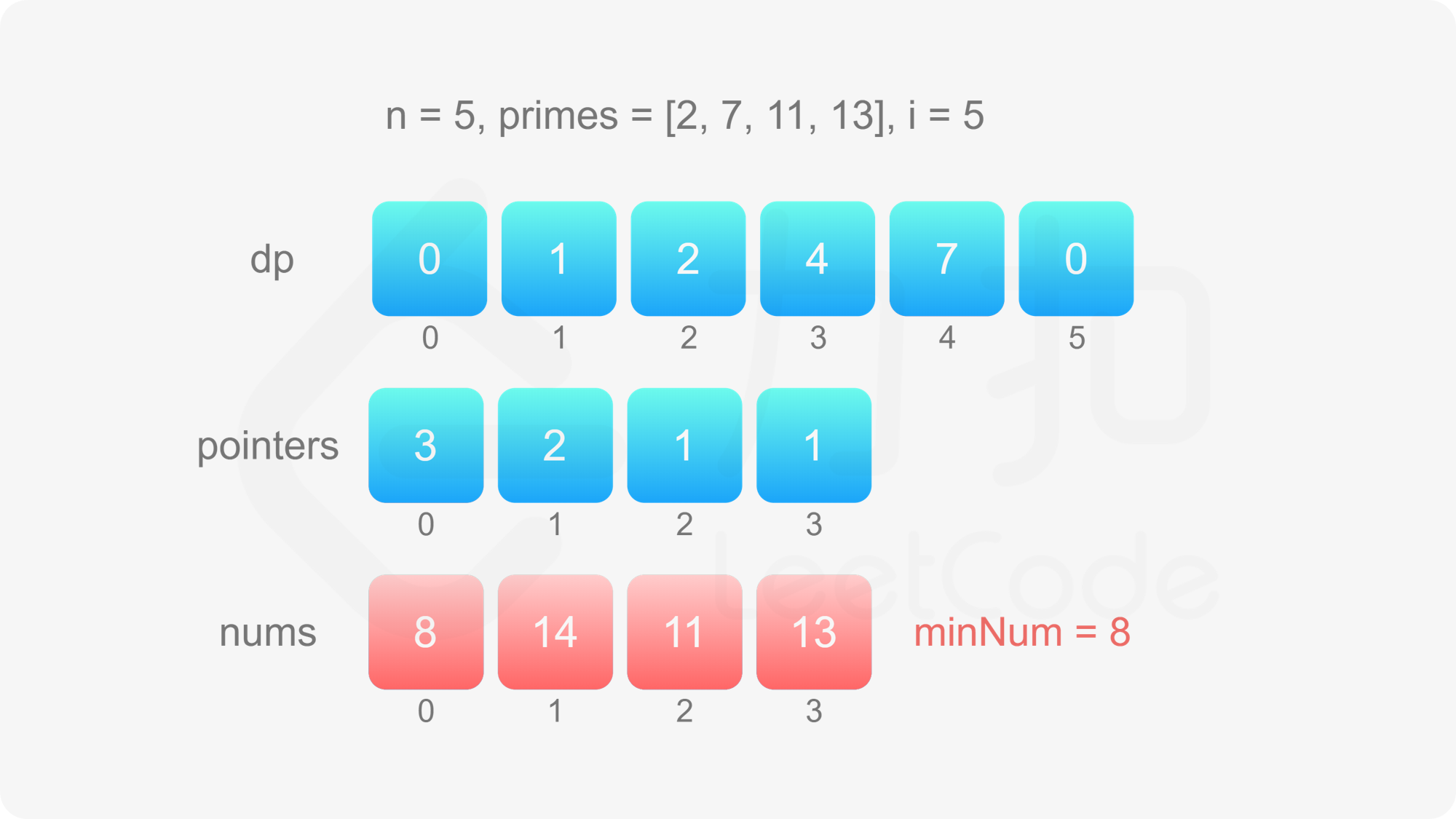
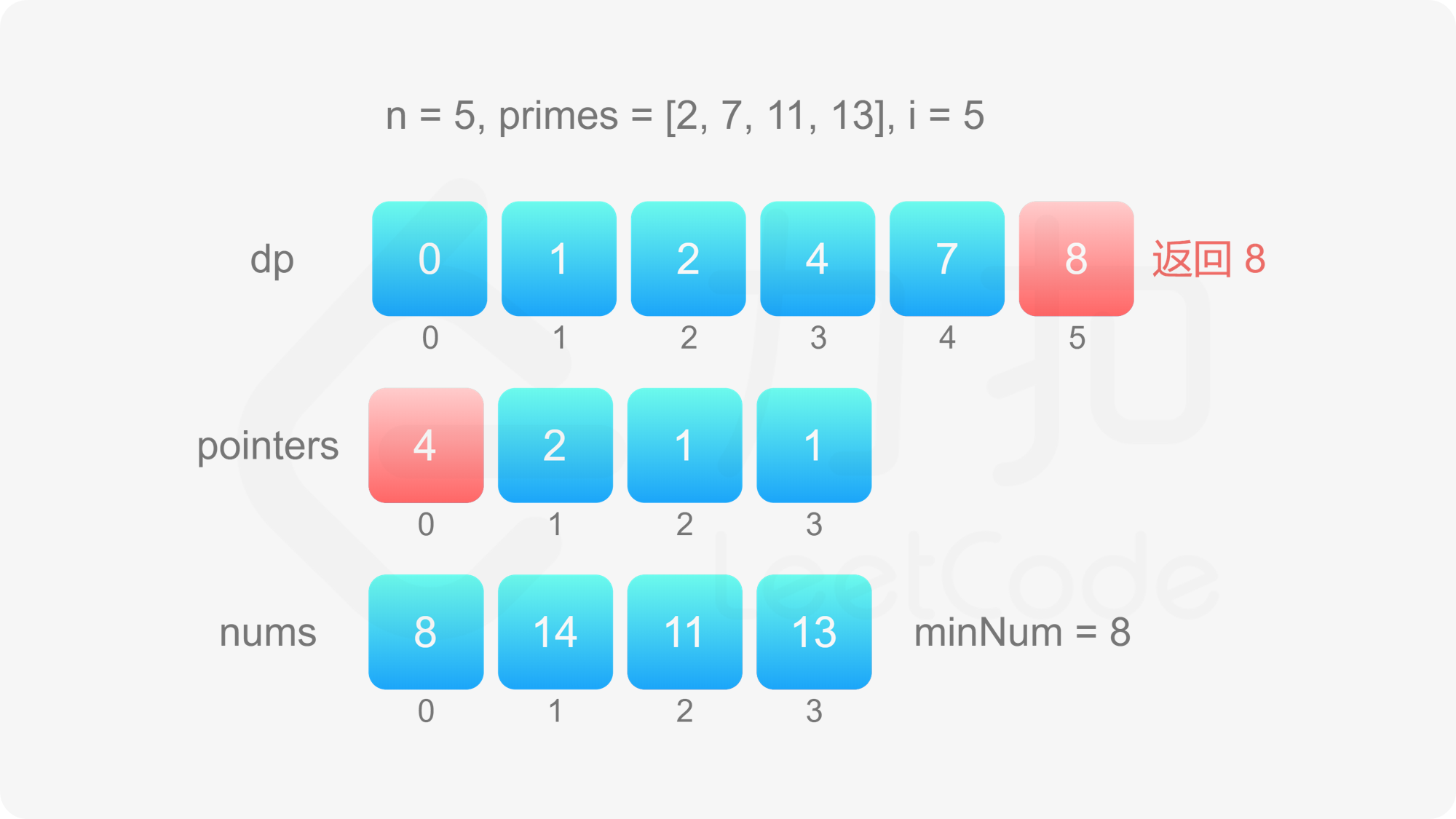
当 $2 \le i \le n$ 时,令 dp}[i]=\underset{0 \le j < m}{\min} {\textit{dp}[\textit{pointers}[j]] \times \textit{primes}[j]\,然后对于每个 $0 \le j < m$,分别比较 dp}[i]$ 和 dp}[\textit{pointers}[j]] \times \textit{primes}[j]$ 是否相等,如果相等则将 pointers}[j]$ 加 $1$。
正确性证明
对于 $i>1$,在计算 dp}[i]$ 时,指针 pointers}[j](0 \le j < m)$ 的含义是使得 dp}[k] \times \textit{primes}[j] > \textit{dp}[i-1]$ 的最小的下标 $k$,即当 $k \ge \textit{pointers}[j]$ 时 dp}[k] \times \textit{primes}[j] > \textit{dp}[i-1]$,当 $k<\textit{pointers}[j]$ 时 dp}[k] \times \textit{primes}[j] \le \textit{dp}[i-1]$。
因此,对于 $i>1$,在计算 dp}[i]$ 时,对任意 $0 \le j < m$,dp}[\textit{pointers}[j]] \times \textit{primes}[j]$ 都大于 dp}[i-1]$,dp}[\textit{pointers}[j]-1] \times \textit{primes}[j]$ 都小于或等于 dp}[i-1]$。令 dp}[i]=\underset{0 \le j < m}{\min} {\textit{dp}[\textit{pointers}[j]] \times \textit{primes}[j]\,则 dp}[i]>\textit{dp}[i-1]$ 且 dp}[i]$ 是大于 dp}[i-1]$ 的最小的超级丑数。
在计算 dp}[i]$ 之后,会更新数组 pointers 中的指针,更新之后的指针将用于计算 dp}[i+1]$,同样满足 dp}[i+1]>\textit{dp}[i]$ 且 dp}[i+1]$ 是大于 dp}[i]$ 的最小的超级丑数。
< ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution {
public int nthSuperUglyNumber(int n, int[] primes) {
int[] dp = new int[n + 1];
int m = primes.length;
int[] pointers = new int[m];
int[] nums = new int[m];
Arrays.fill(nums, 1);
for (int i = 1; i <= n; i++) {
int minNum = Arrays.stream(nums).min().getAsInt();
dp[i] = minNum;
for (int j = 0; j < m; j++) {
if (nums[j] == minNum) {
pointers[j]++;
nums[j] = dp[pointers[j]] * primes[j];
}
}
}
return dp[n];
}
}
|
[sol1-C#]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| public class Solution {
public int NthSuperUglyNumber(int n, int[] primes) {
int[] dp = new int[n + 1];
int m = primes.Length;
int[] pointers = new int[m];
int[] nums = new int[m];
Array.Fill(nums, 1);
for (int i = 1; i <= n; i++) {
int minNum = nums.Min();
dp[i] = minNum;
for (int j = 0; j < m; j++) {
if (nums[j] == minNum) {
pointers[j]++;
nums[j] = dp[pointers[j]] * primes[j];
}
}
}
return dp[n];
}
}
|
[sol1-JavaScript]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| var nthSuperUglyNumber = function(n, primes) {
const dp = new Array(n + 1).fill(0);
const m = primes.length;
const pointers = new Array(m).fill(0);
const nums = new Array(m).fill(1);
for (let i = 1; i <= n; i++) {
let minNum = Number.MAX_SAFE_INTEGER;
for (let j = 0; j < m; j++) {
minNum = Math.min(minNum, nums[j]);
}
dp[i] = minNum;
for (let j = 0; j < m; j++) {
if (nums[j] == minNum) {
pointers[j]++;
nums[j] = dp[pointers[j]] * primes[j];
}
}
}
return dp[n];
};
|
[sol1-Python3]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| class Solution:
def nthSuperUglyNumber(self, n: int, primes: List[int]) -> int:
dp = [0] * (n + 1)
m = len(primes)
pointers = [0] * m
nums = [1] * m
for i in range(1, n + 1):
min_num = min(nums)
dp[i] = min_num
for j in range(m):
if nums[j] == min_num:
pointers[j] += 1
nums[j] = dp[pointers[j]] * primes[j]
return dp[n]
|
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class Solution {
public:
int nthSuperUglyNumber(int n, vector<int>& primes) {
vector<long> dp(n + 1);
int m = primes.size();
vector<int> pointers(m, 0);
vector<long> nums(m, 1);
for (int i = 1; i <= n; i++) {
long minNum = INT_MAX;
for (int j = 0; j < m; j++) {
minNum = min(minNum, nums[j]);
}
dp[i] = minNum;
for (int j = 0; j < m; j++) {
if (nums[j] == minNum) {
pointers[j]++;
nums[j] = dp[pointers[j]] * primes[j];
}
}
}
return dp[n];
}
};
|
[sol1-C]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| int nthSuperUglyNumber(int n, int* primes, int primesSize) {
long dp[n + 1];
int pointers[primesSize];
for (int i = 0; i < primesSize; i++) {
pointers[i] = 0;
}
long nums[primesSize];
for (int i = 0; i < primesSize; i++) {
nums[i] = 1;
}
for (int i = 1; i <= n; i++) {
long minNum = INT_MAX;
for (int j = 0; j < primesSize; j++) {
minNum = fmin(minNum, nums[j]);
}
dp[i] = minNum;
for (int j = 0; j < primesSize; j++) {
if (nums[j] == minNum) {
pointers[j]++;
nums[j] = dp[pointers[j]] * primes[j];
}
}
}
return dp[n];
}
|
[sol1-Golang]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| func nthSuperUglyNumber(n int, primes []int) int {
dp := make([]int, n+1)
m := len(primes)
pointers := make([]int, m)
nums := make([]int, m)
for i := range nums {
nums[i] = 1
}
for i := 1; i <= n; i++ {
minNum := math.MaxInt64
for j := range pointers {
minNum = min(minNum, nums[j])
}
dp[i] = minNum
for j := range nums {
if nums[j] == minNum {
pointers[j]++
nums[j] = dp[pointers[j]] * primes[j]
}
}
}
return dp[n]
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
|
复杂度分析
时间复杂度:$O(nm)$,其中 $n$ 是待求的超级丑数的编号,$m$ 是数组 primes 的长度。需要计算数组 dp 中的 $n$ 个元素,每个元素的计算都需要 $O(m)$ 的时间。
空间复杂度:$O(n+m)$,其中 $n$ 是待求的超级丑数的编号,$m$ 是数组 primes 的长度。需要创建数组 dp、数组 pointers 和数组 nums,空间分别是 $O(n)$、$O(m) 和 $O(m)$。
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>