0319-灯泡开关

初始时有 n __ 个灯泡处于关闭状态。第一轮，你将会打开所有灯泡。接下来的第二轮，你将会每两个灯泡关闭第二个。

第三轮，你每三个灯泡就切换第三个灯泡的开关（即，打开变关闭，关闭变打开）。第 i 轮，你每 i 个灯泡就切换第 i 个灯泡的开关。直到第 n
轮，你只需要切换最后一个灯泡的开关。

找出并返回 n _ _ 轮后有多少个亮着的灯泡。

示例 1：

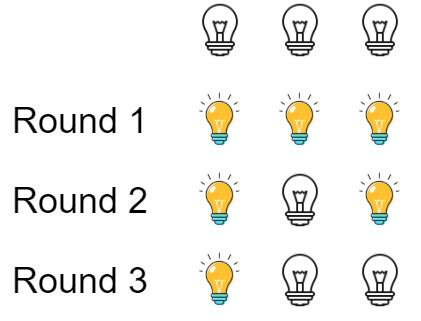
**输入：** n = **** 3
**输出：** 1 
**解释：**
初始时, 灯泡状态 **[关闭, 关闭, 关闭]**.
第一轮后, 灯泡状态 **[开启, 开启, 开启]**.
第二轮后, 灯泡状态 **[开启, 关闭, 开启]**.
第三轮后, 灯泡状态 **[开启, 关闭, 关闭]**. 

你应该返回 1，因为只有一个灯泡还亮着。

示例 2：

**输入：** n = 0
**输出：** 0

示例 3：

**输入：** n = 1
**输出：** 1

提示：

• 0 <= n <= 109

方法一：数学

思路与算法

如果我们将所有的灯泡从左到右依次编号为 $1, 2, \cdots, n$，那么可以发现：

在第 $i$ 轮时，我们会将所有编号为 $i$ 的倍数的灯泡进行切换。

因此，对于第 $k$ 个灯泡，它被切换的次数恰好就是 $k$ 的约数个数。如果 $k$ 有偶数个约数，那么最终第 $k$ 个灯泡的状态为暗；如果 $k$ 有奇数个约数，那么最终第 $k$ 个灯泡的状态为亮。

对于 $k$ 而言，如果它有约数 $x$，那么一定有约数 $\dfrac{k}{x。因此只要当 $x^2 \neq k$ 时，约数都是「成对」出现的。这就说明，只有当 $k$ 是「完全平方数」时，它才会有奇数个约数，否则一定有偶数个约数。

因此我们只需要找出 $1, 2, \cdots, n$ 中的完全平方数的个数即可，答案即为 $\lfloor \sqrt{n} \rfloor$，其中 $\lfloor \cdot \rfloor$ 表示向下取整。

细节

由于 $\sqrt{n 涉及到浮点数运算，为了保证不出现精度问题，我们可以计算 $\sqrt{n + \dfrac{1}{2}，这样可以保证计算出来的结果向下取整在 $32$ 位整数范围内一定正确。

代码

[sol1-C++]

class Solution {
public:
    int bulbSwitch(int n) {
        return sqrt(n + 0.5);
    }
};

[sol1-Java]

class Solution {
    public int bulbSwitch(int n) {
        return (int) Math.sqrt(n + 0.5);
    }
}

[sol1-C#]

public class Solution {
    public int BulbSwitch(int n) {
        return (int) Math.Sqrt(n + 0.5);
    }
}

[sol1-Python3]

class Solution:
    def bulbSwitch(self, n: int) -> int:
        return int(sqrt(n + 0.5))

[sol1-JavaScript]

var bulbSwitch = function(n) {
    return Math.floor(Math.sqrt(n + 0.5));
};

[sol1-Golang]

func bulbSwitch(n int) int {
    return int(math.Sqrt(float64(n) + 0.5))
}

复杂度分析

• 时间复杂度：$O(1)$。

• 空间复杂度：$O(1)$。