给定长度分别为 m 和 n 的两个数组,其元素由 0-9 构成,表示两个自然数各位上的数字。现在从这两个数组中选出 k (k <= m + n) 个数字拼接成一个新的数,要求从同一个数组中取出的数字保持其在原数组中的相对顺序。
求满足该条件的最大数。结果返回一个表示该最大数的长度为 k 的数组。
说明: 请尽可能地优化你算法的时间和空间复杂度。
示例 1:
**输入:**
nums1 = [3, 4, 6, 5]
nums2 = [9, 1, 2, 5, 8, 3]
k = 5
**输出:**
[9, 8, 6, 5, 3]
示例 2:
**输入:**
nums1 = [6, 7]
nums2 = [6, 0, 4]
k = 5
**输出:**
[6, 7, 6, 0, 4]
示例 3:
**输入:**
nums1 = [3, 9]
nums2 = [8, 9]
k = 3
**输出:**
[9, 8, 9]
方法一:单调栈 为了找到长度为 $k$ 的最大数,需要从两个数组中分别选出最大的子序列,这两个子序列的长度之和为 $k$,然后将这两个子序列合并得到最大数。两个子序列的长度最小为 $0$,最大不能超过 $k$ 且不能超过对应的数组长度。
令数组 nums}_1$ 的长度为 $m$,数组 nums}_2$ 的长度为 $n$,则需要从数组 nums}_1$ 中选出长度为 $x$ 的子序列,以及从数组 nums}_2$ 中选出长度为 $y$ 的子序列,其中 $x+y=k$,且满足 $0 \le x \le m$ 和 $0 \le y \le n$。需要遍历所有可能的 $x$ 和 $y$ 的值,对于每一组 $x$ 和 $y$ 的值,得到最大数。在整个过程中维护可以通过拼接得到的最大数。
对于每一组 $x$ 和 $y$ 的值,得到最大数的过程分成两步,第一步是分别从两个数组中得到指定长度的最大子序列,第二步是将两个最大子序列合并。
第一步可以通过单调栈实现。单调栈满足从栈底到栈顶的元素单调递减,从左到右遍历数组,遍历过程中维护单调栈内的元素,需要保证遍历结束之后单调栈内的元素个数等于指定的最大子序列的长度。遍历结束之后,将从栈底到栈顶的元素依次拼接,即得到最大子序列。
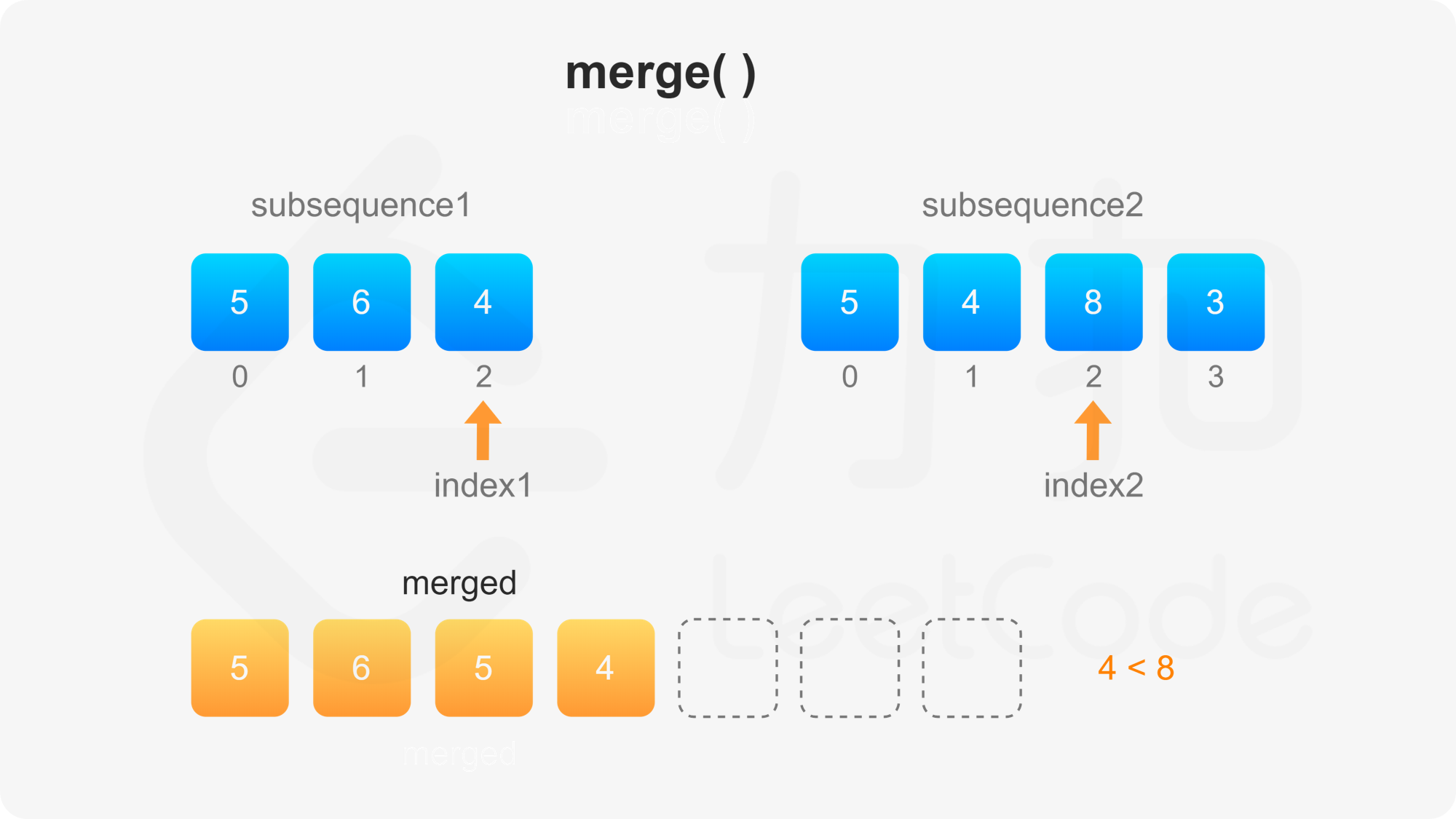
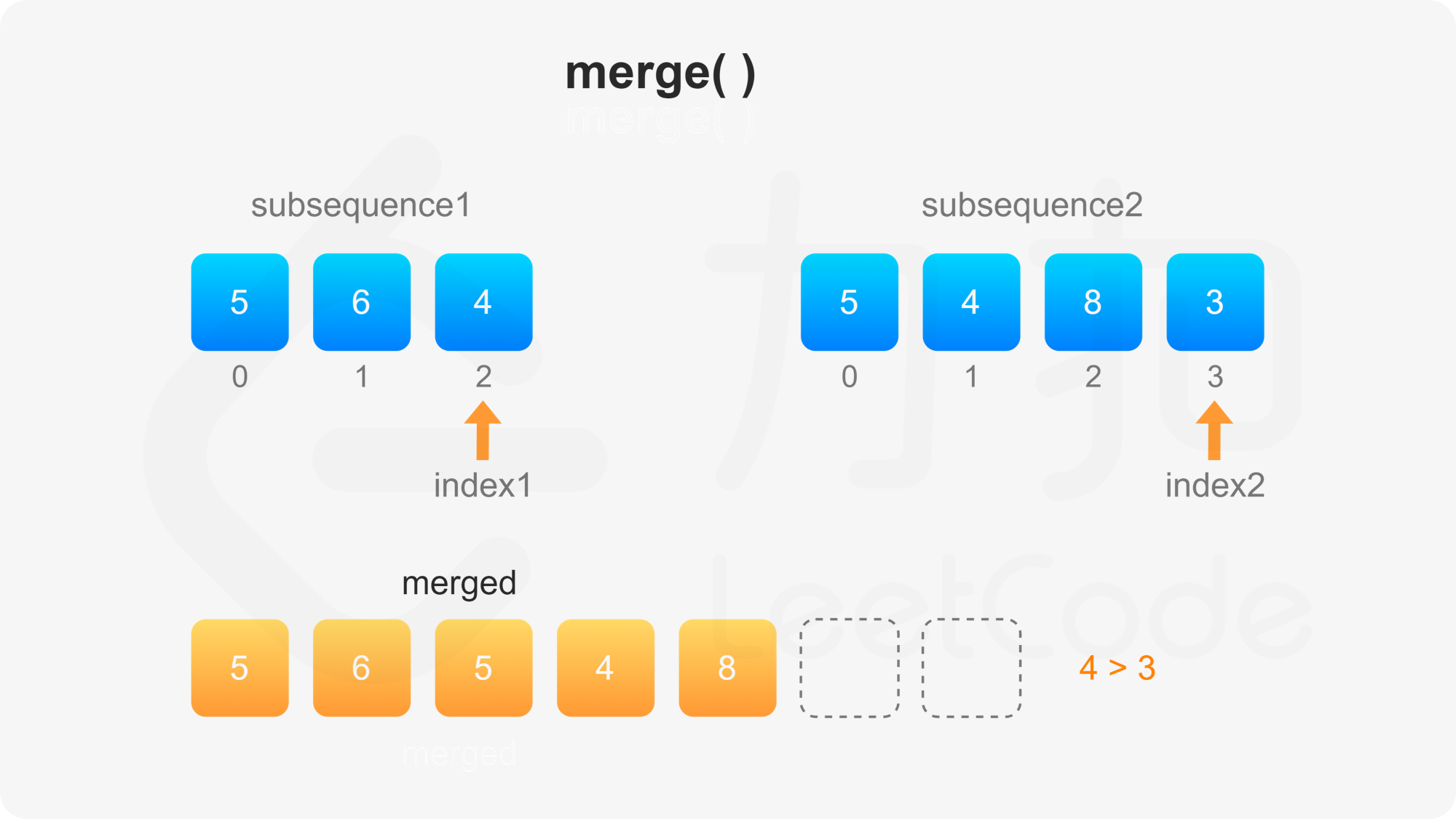
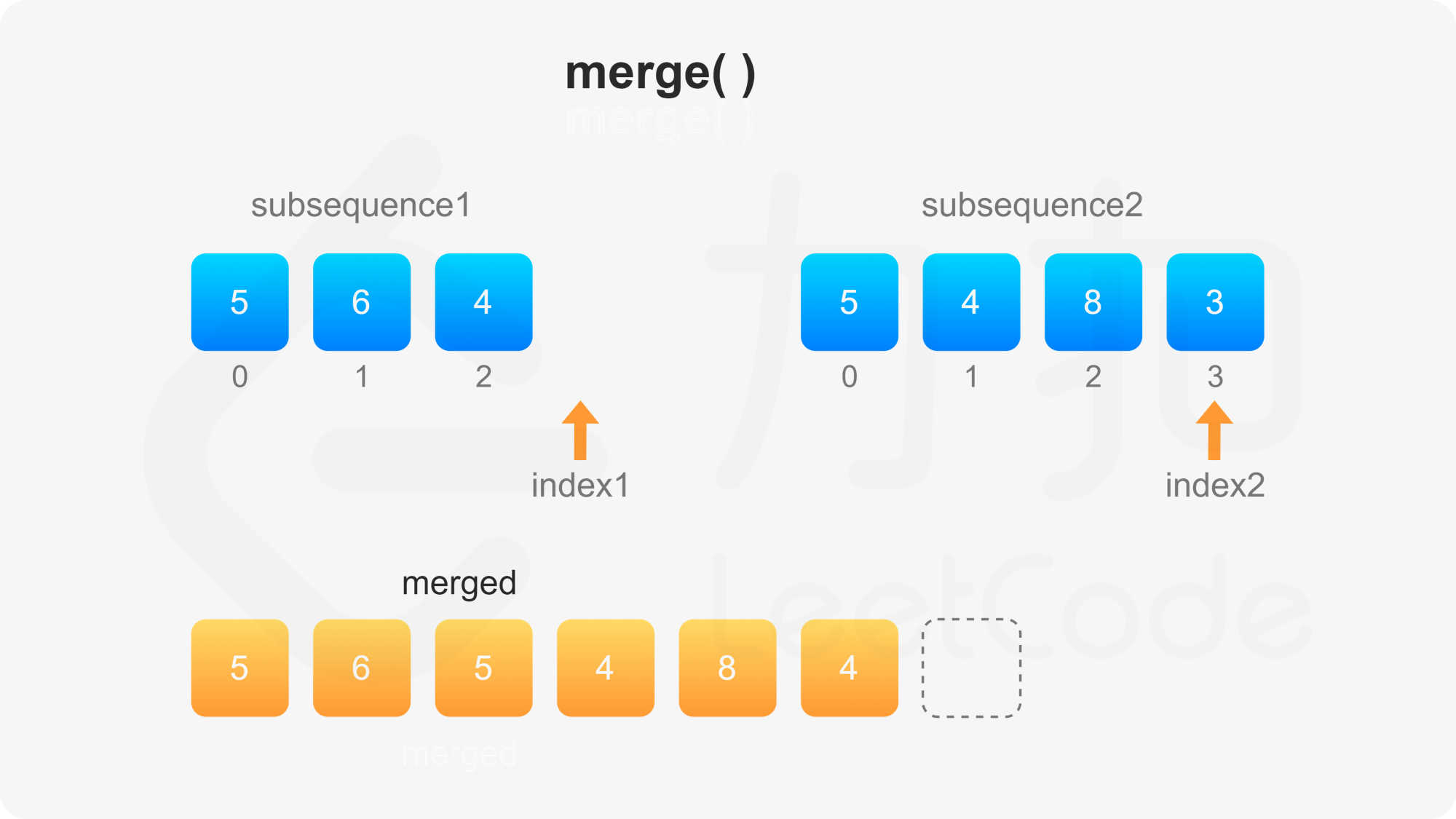
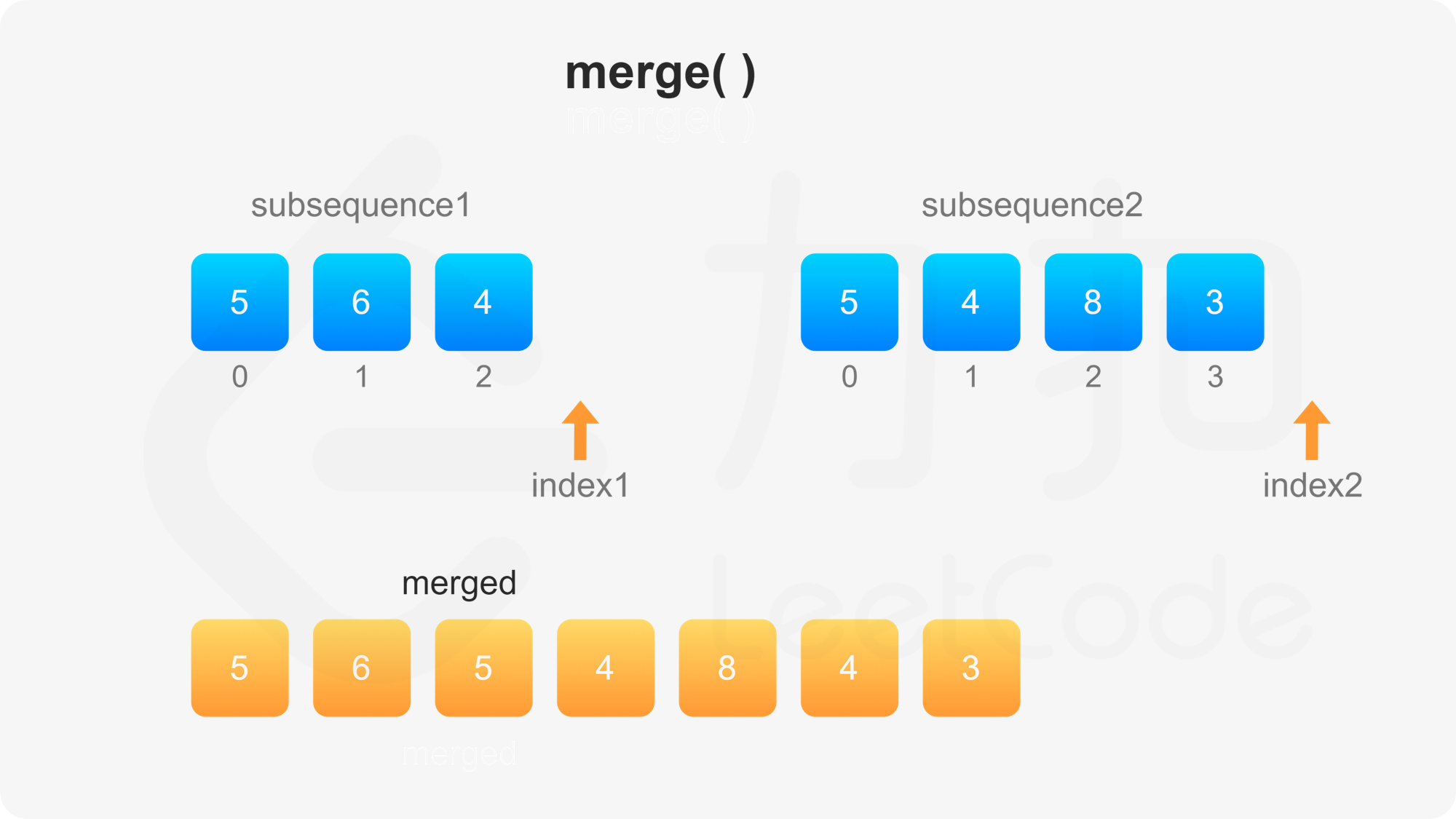
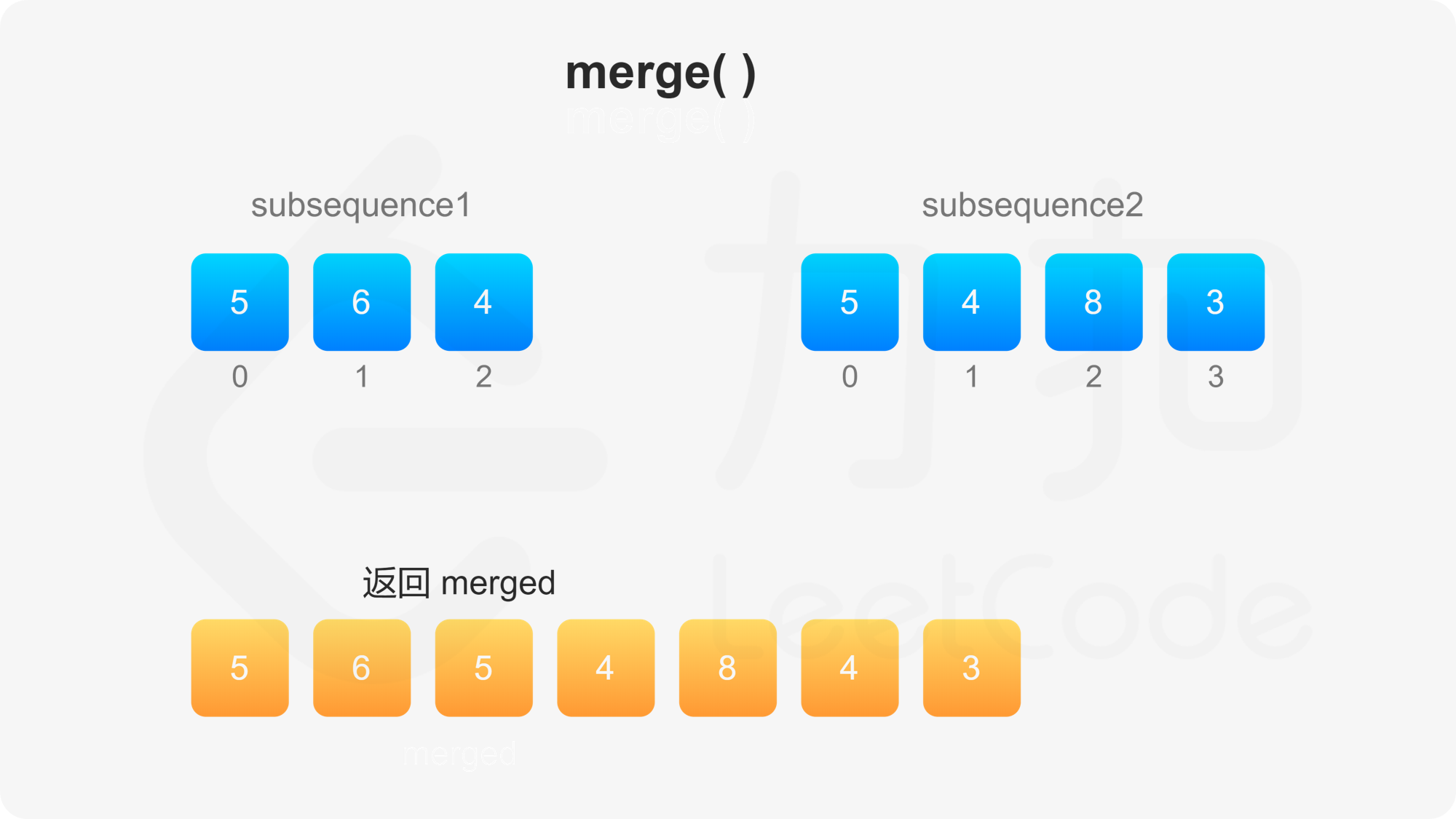
第二步需要自定义比较方法。首先比较两个子序列的当前元素,如果两个当前元素不同,则选其中较大的元素作为下一个合并的元素,否则需要比较后面的所有元素才能决定选哪个元素作为下一个合并的元素。
<
在下面的代码中,单调栈使用数组实现,数组最左侧为栈底。使用数组实现,可以直接从左到右遍历数组得到最大子序列。
[sol1-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 class Solution { public int [] maxNumber(int [] nums1, int [] nums2, int k) { int m = nums1.length, n = nums2.length; int [] maxSubsequence = new int [k]; int start = Math.max(0 , k - n), end = Math.min(k, m); for (int i = start; i <= end; i++) { int [] subsequence1 = maxSubsequence(nums1, i); int [] subsequence2 = maxSubsequence(nums2, k - i); int [] curMaxSubsequence = merge(subsequence1, subsequence2); if (compare(curMaxSubsequence, 0 , maxSubsequence, 0 ) > 0 ) { System.arraycopy(curMaxSubsequence, 0 , maxSubsequence, 0 , k); } } return maxSubsequence; } public int [] maxSubsequence(int [] nums, int k) { int length = nums.length; int [] stack = new int [k]; int top = -1 ; int remain = length - k; for (int i = 0 ; i < length; i++) { int num = nums[i]; while (top >= 0 && stack[top] < num && remain > 0 ) { top--; remain--; } if (top < k - 1 ) { stack[++top] = num; } else { remain--; } } return stack; } public int [] merge(int [] subsequence1, int [] subsequence2) { int x = subsequence1.length, y = subsequence2.length; if (x == 0 ) { return subsequence2; } if (y == 0 ) { return subsequence1; } int mergeLength = x + y; int [] merged = new int [mergeLength]; int index1 = 0 , index2 = 0 ; for (int i = 0 ; i < mergeLength; i++) { if (compare(subsequence1, index1, subsequence2, index2) > 0 ) { merged[i] = subsequence1[index1++]; } else { merged[i] = subsequence2[index2++]; } } return merged; } public int compare (int [] subsequence1, int index1, int [] subsequence2, int index2) { int x = subsequence1.length, y = subsequence2.length; while (index1 < x && index2 < y) { int difference = subsequence1[index1] - subsequence2[index2]; if (difference != 0 ) { return difference; } index1++; index2++; } return (x - index1) - (y - index2); } }
[sol1-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 class Solution {public : vector<int > maxNumber (vector<int >& nums1, vector<int >& nums2, int k) { int m = nums1.size (), n = nums2.size (); vector<int > maxSubsequence (k, 0 ) ; int start = max (0 , k - n), end = min (k, m); for (int i = start; i <= end; i++) { vector<int > subsequence1 (MaxSubsequence(nums1, i)) ; vector<int > subsequence2 (MaxSubsequence(nums2, k - i)) ; vector<int > curMaxSubsequence (merge(subsequence1, subsequence2)) ; if (compare (curMaxSubsequence, 0 , maxSubsequence, 0 ) > 0 ) { maxSubsequence.swap (curMaxSubsequence); } } return maxSubsequence; } vector<int > MaxSubsequence (vector<int >& nums, int k) { int length = nums.size (); vector<int > stack (k, 0 ) ; int top = -1 ; int remain = length - k; for (int i = 0 ; i < length; i++) { int num = nums[i]; while (top >= 0 && stack[top] < num && remain > 0 ) { top--; remain--; } if (top < k - 1 ) { stack[++top] = num; } else { remain--; } } return stack; } vector<int > merge (vector<int >& subsequence1, vector<int >& subsequence2) { int x = subsequence1.size (), y = subsequence2.size (); if (x == 0 ) { return subsequence2; } if (y == 0 ) { return subsequence1; } int mergeLength = x + y; vector<int > merged (mergeLength) ; int index1 = 0 , index2 = 0 ; for (int i = 0 ; i < mergeLength; i++) { if (compare (subsequence1, index1, subsequence2, index2) > 0 ) { merged[i] = subsequence1[index1++]; } else { merged[i] = subsequence2[index2++]; } } return merged; } int compare (vector<int >& subsequence1, int index1, vector<int >& subsequence2, int index2) int x = subsequence1.size (), y = subsequence2.size (); while (index1 < x && index2 < y) { int difference = subsequence1[index1] - subsequence2[index2]; if (difference != 0 ) { return difference; } index1++; index2++; } return (x - index1) - (y - index2); } };
[sol1-JavaScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 var maxNumber = function (nums1, nums2, k ) { const m = nums1.length , n = nums2.length ; const maxSubsequence = new Array (k).fill (0 ); let start = Math .max (0 , k - n), end = Math .min (k, m); for (let i = start; i <= end; i++) { const subsequence1 = new MaxSubsequence (nums1, i); const subsequence2 = new MaxSubsequence (nums2, k - i); const curMaxSubsequence = merge (subsequence1, subsequence2); if (compare (curMaxSubsequence, 0 , maxSubsequence, 0 ) > 0 ) { maxSubsequence.splice (0 , k, ...curMaxSubsequence); } } return maxSubsequence; }; var MaxSubsequence = function (nums, k ) { const length = nums.length ; const stack = new Array (k).fill (0 ); let top = -1 ; let remain = length - k; for (let i = 0 ; i < length; i++) { const num = nums[i]; while (top >= 0 && stack[top] < num && remain > 0 ) { top--; remain--; } if (top < k - 1 ) { stack[++top] = num; } else { remain--; } } return stack; } const merge = (subsequence1, subsequence2 ) => { const x = subsequence1.length , y = subsequence2.length ; if (x === 0 ) { return subsequence2; } if (y === 0 ) { return subsequence1; } const mergeLength = x + y; const merged = new Array (mergeLength).fill (0 ); let index1 = 0 , index2 = 0 ; for (let i = 0 ; i < mergeLength; i++) { if (compare (subsequence1, index1, subsequence2, index2) > 0 ) { merged[i] = subsequence1[index1++]; } else { merged[i] = subsequence2[index2++]; } } return merged; } const compare = (subsequence1, index1, subsequence2, index2 ) => { const x = subsequence1.length , y = subsequence2.length ; while (index1 < x && index2 < y) { const difference = subsequence1[index1] - subsequence2[index2]; if (difference !== 0 ) { return difference; } index1++; index2++; } return (x - index1) - (y - index2); }
[sol1-Python3] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 class Solution : def maxNumber (self, nums1: List [int ], nums2: List [int ], k: int ) -> List [int ]: m, n = len (nums1), len (nums2) maxSubsequence = [0 ] * k start, end = max (0 , k - n), min (k, m) for i in range (start, end + 1 ): subsequence1 = self.getMaxSubsequence(nums1, i) subsequence2 = self.getMaxSubsequence(nums2, k - i) curMaxSubsequence = self.merge(subsequence1, subsequence2) if self.compare(curMaxSubsequence, 0 , maxSubsequence, 0 ) > 0 : maxSubsequence = curMaxSubsequence return maxSubsequence def getMaxSubsequence (self, nums: List [int ], k: int ) -> int : stack = [0 ] * k top = -1 remain = len (nums) - k for i, num in enumerate (nums): while top >= 0 and stack[top] < num and remain > 0 : top -= 1 remain -= 1 if top < k - 1 : top += 1 stack[top] = num else : remain -= 1 return stack def merge (self, subsequence1: List [int ], subsequence2: List [int ] ) -> List [int ]: x, y = len (subsequence1), len (subsequence2) if x == 0 : return subsequence2 if y == 0 : return subsequence1 mergeLength = x + y merged = list () index1 = index2 = 0 for _ in range (mergeLength): if self.compare(subsequence1, index1, subsequence2, index2) > 0 : merged.append(subsequence1[index1]) index1 += 1 else : merged.append(subsequence2[index2]) index2 += 1 return merged def compare (self, subsequence1: List [int ], index1: int , subsequence2: List [int ], index2: int ) -> int : x, y = len (subsequence1), len (subsequence2) while index1 < x and index2 < y: difference = subsequence1[index1] - subsequence2[index2] if difference != 0 : return difference index1 += 1 index2 += 1 return (x - index1) - (y - index2)
[sol1-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 func maxSubsequence (a []int , k int ) int ) { for i, v := range a { for len (s) > 0 && len (s)+len (a)-1 -i >= k && v > s[len (s)-1 ] { s = s[:len (s)-1 ] } if len (s) < k { s = append (s, v) } } return } func lexicographicalLess (a, b []int ) bool { for i := 0 ; i < len (a) && i < len (b); i++ { if a[i] != b[i] { return a[i] < b[i] } } return len (a) < len (b) } func merge (a, b []int ) int { merged := make ([]int , len (a)+len (b)) for i := range merged { if lexicographicalLess(a, b) { merged[i], b = b[0 ], b[1 :] } else { merged[i], a = a[0 ], a[1 :] } } return merged } func maxNumber (nums1, nums2 []int , k int ) int ) { start := 0 if k > len (nums2) { start = k - len (nums2) } for i := start; i <= k && i <= len (nums1); i++ { s1 := maxSubsequence(nums1, i) s2 := maxSubsequence(nums2, k-i) merged := merge(s1, s2) if lexicographicalLess(res, merged) { res = merged } } return }
[sol1-C] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 int compare (int * subseq1, int subseq1Size, int index1, int * subseq2, int subseq2Size, int index2) { while (index1 < subseq1Size && index2 < subseq2Size) { int difference = subseq1[index1] - subseq2[index2]; if (difference != 0 ) { return difference; } index1++; index2++; } return (subseq1Size - index1) - (subseq2Size - index2); } int * merge (int * subseq1, int subseq1Size, int * subseq2, int subseq2Size) { if (subseq1Size == 0 ) { return subseq2; } if (subseq2Size == 0 ) { return subseq1; } int mergeLength = subseq1Size + subseq2Size; int * merged = malloc (sizeof (int ) * (subseq1Size + subseq2Size)); int index1 = 0 , index2 = 0 ; for (int i = 0 ; i < mergeLength; i++) { if (compare(subseq1, subseq1Size, index1, subseq2, subseq2Size, index2) > 0 ) { merged[i] = subseq1[index1++]; } else { merged[i] = subseq2[index2++]; } } return merged; } int * MaxSubsequence (int * nums, int numsSize, int k) { int * stack = malloc (sizeof (int ) * k); memset (stack , 0 , sizeof (int ) * k); int top = -1 ; int remain = numsSize - k; for (int i = 0 ; i < numsSize; i++) { int num = nums[i]; while (top >= 0 && stack [top] < num && remain > 0 ) { top--; remain--; } if (top < k - 1 ) { stack [++top] = num; } else { remain--; } } return stack ; } void swap (int ** a, int ** b) { int * tmp = *a; *a = *b, *b = tmp; } int * maxNumber (int * nums1, int nums1Size, int * nums2, int nums2Size, int k, int * returnSize) { int * maxSubsequence = malloc (sizeof (int ) * k); memset (maxSubsequence, 0 , sizeof (int ) * k); *returnSize = k; int start = fmax(0 , k - nums2Size), end = fmin(k, nums1Size); for (int i = start; i <= end; i++) { int * subseq1 = MaxSubsequence(nums1, nums1Size, i); int * subseq2 = MaxSubsequence(nums2, nums2Size, k - i); int * curMaxSubsequence = merge(subseq1, i, subseq2, k - i); if (compare(curMaxSubsequence, k, 0 , maxSubsequence, k, 0 ) > 0 ) { swap(&curMaxSubsequence, &maxSubsequence); } } return maxSubsequence; }
复杂度分析
时间复杂度:$O(k(m+n+k^2))$,其中 $m$ 和 $n$ 分别是数组 nums}_1$ 和 nums}_2$ 的长度,$k$ 是拼接最大数的长度。
空间复杂度:$O(k)$,其中 $k$ 是拼接最大数的长度。每次从两个数组得到两个子序列,两个子序列的长度之和为 $k$。
 ,
, ,
,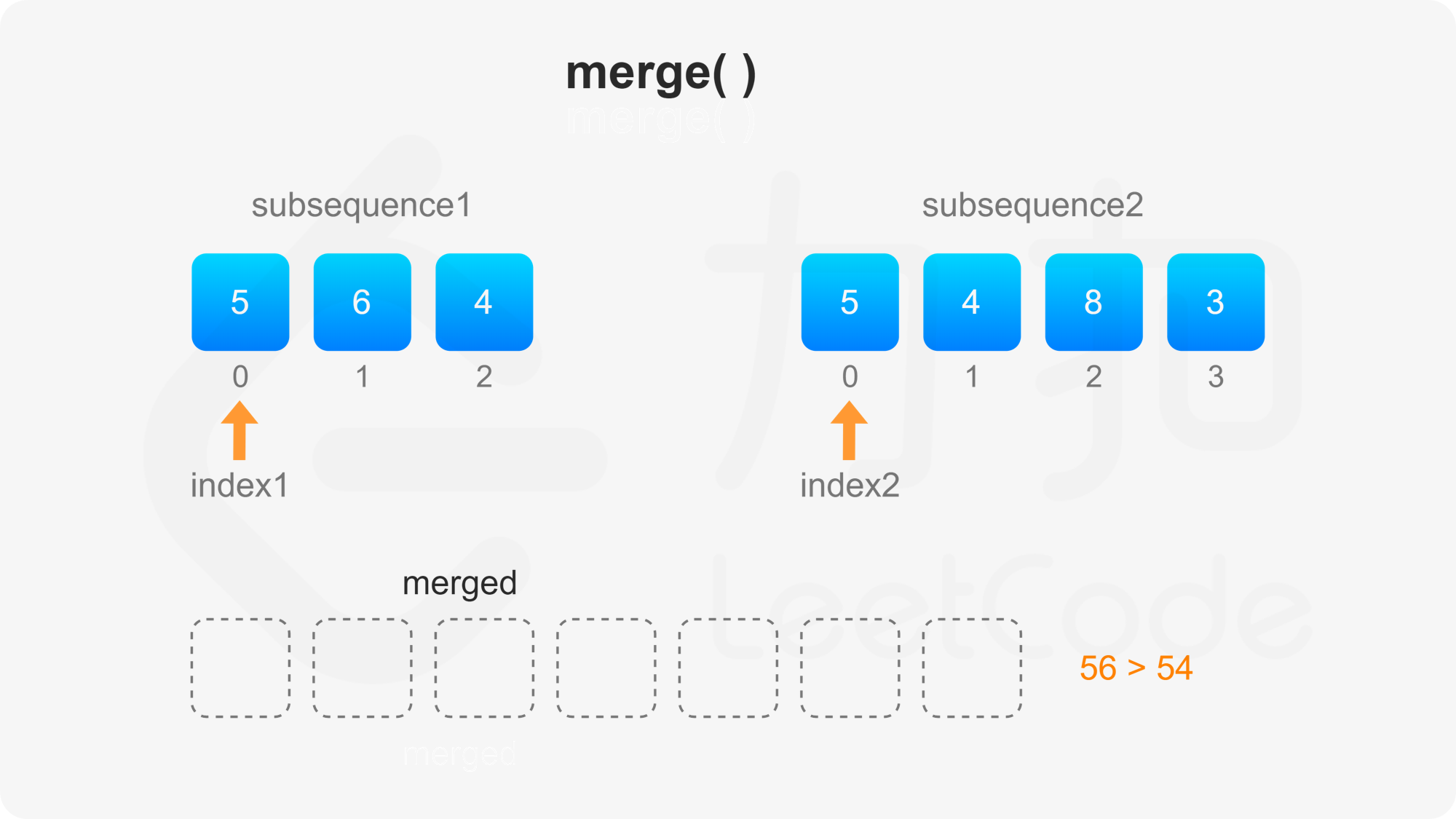 ,
,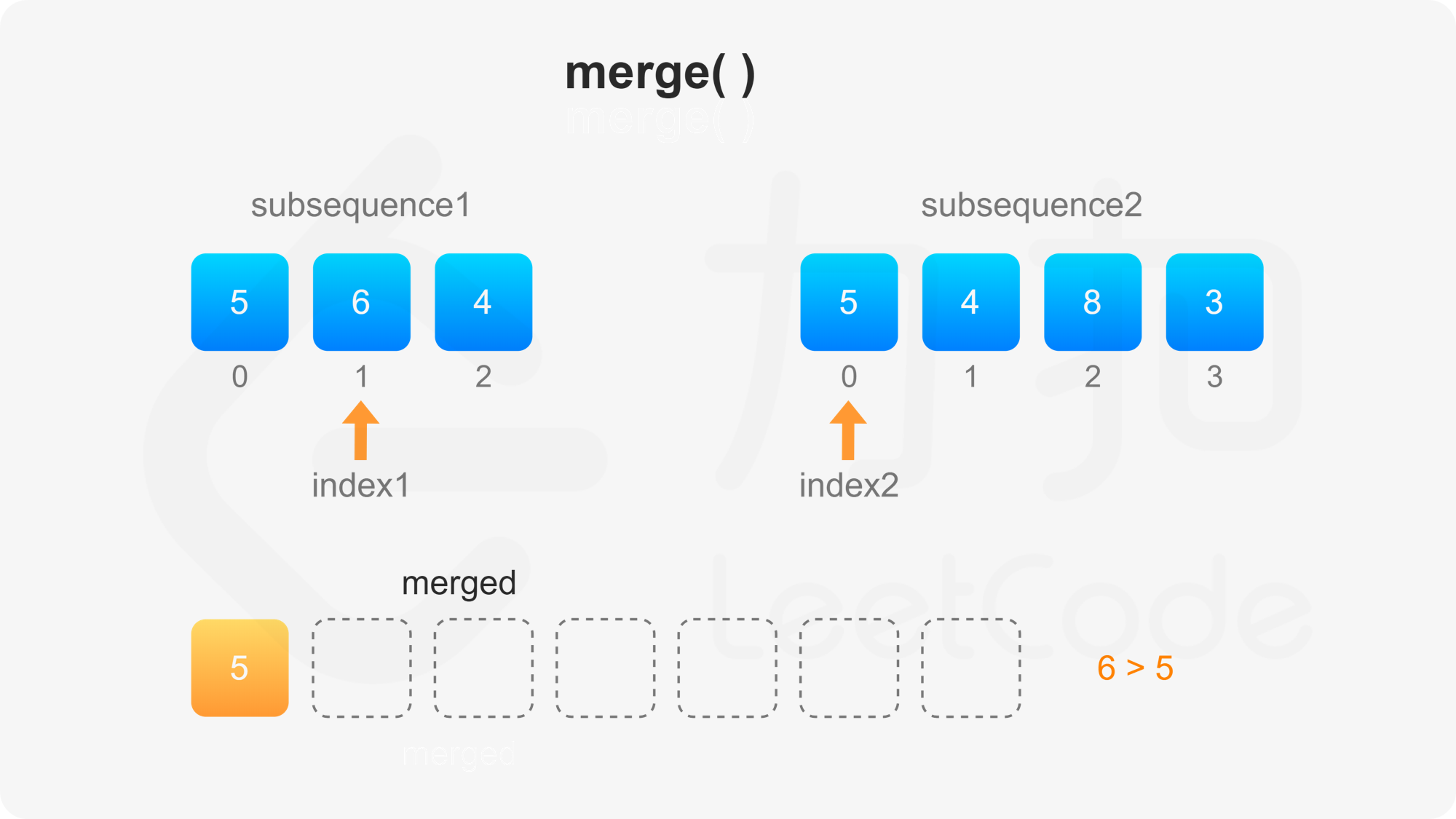 ,
,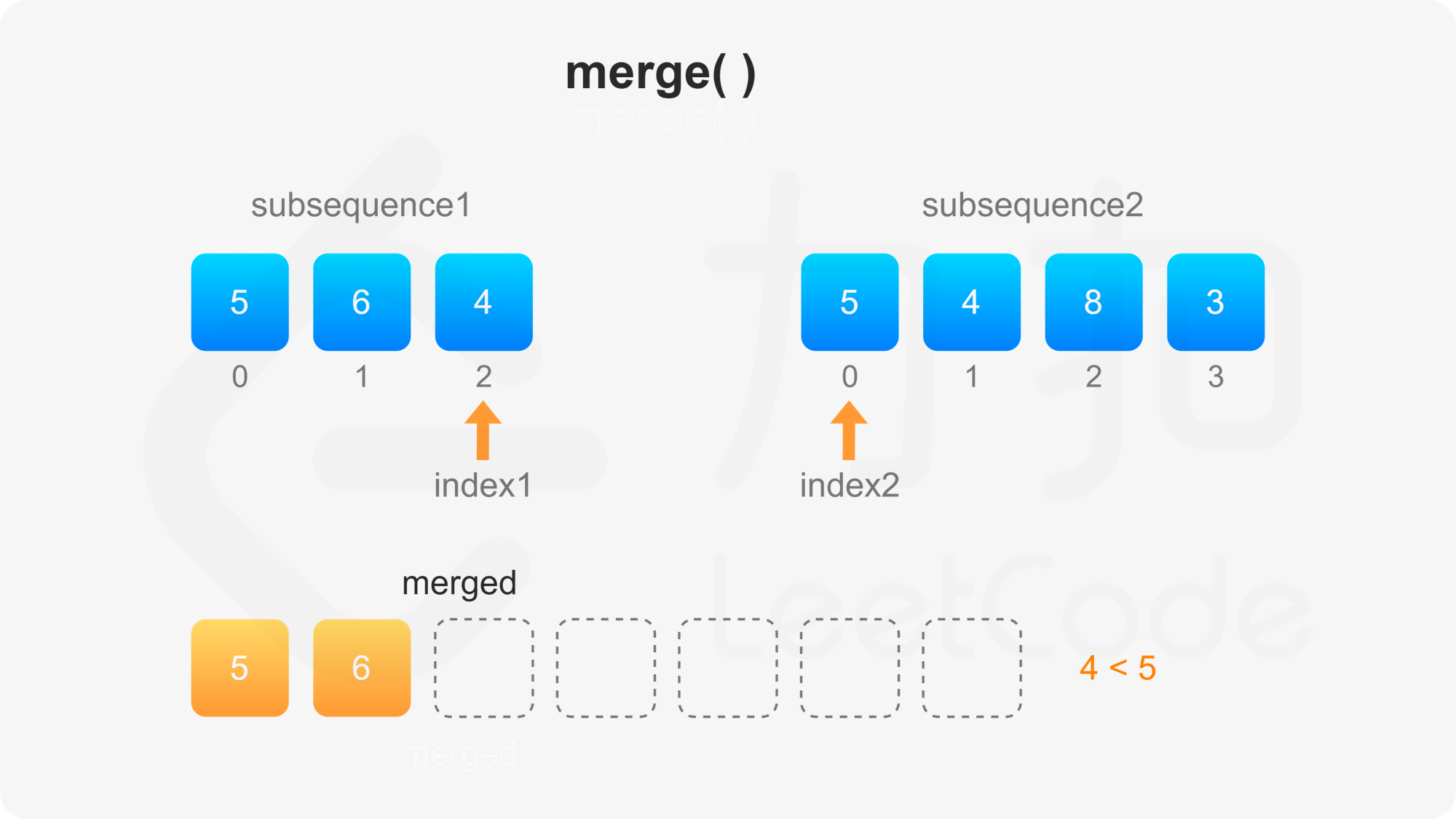 ,
,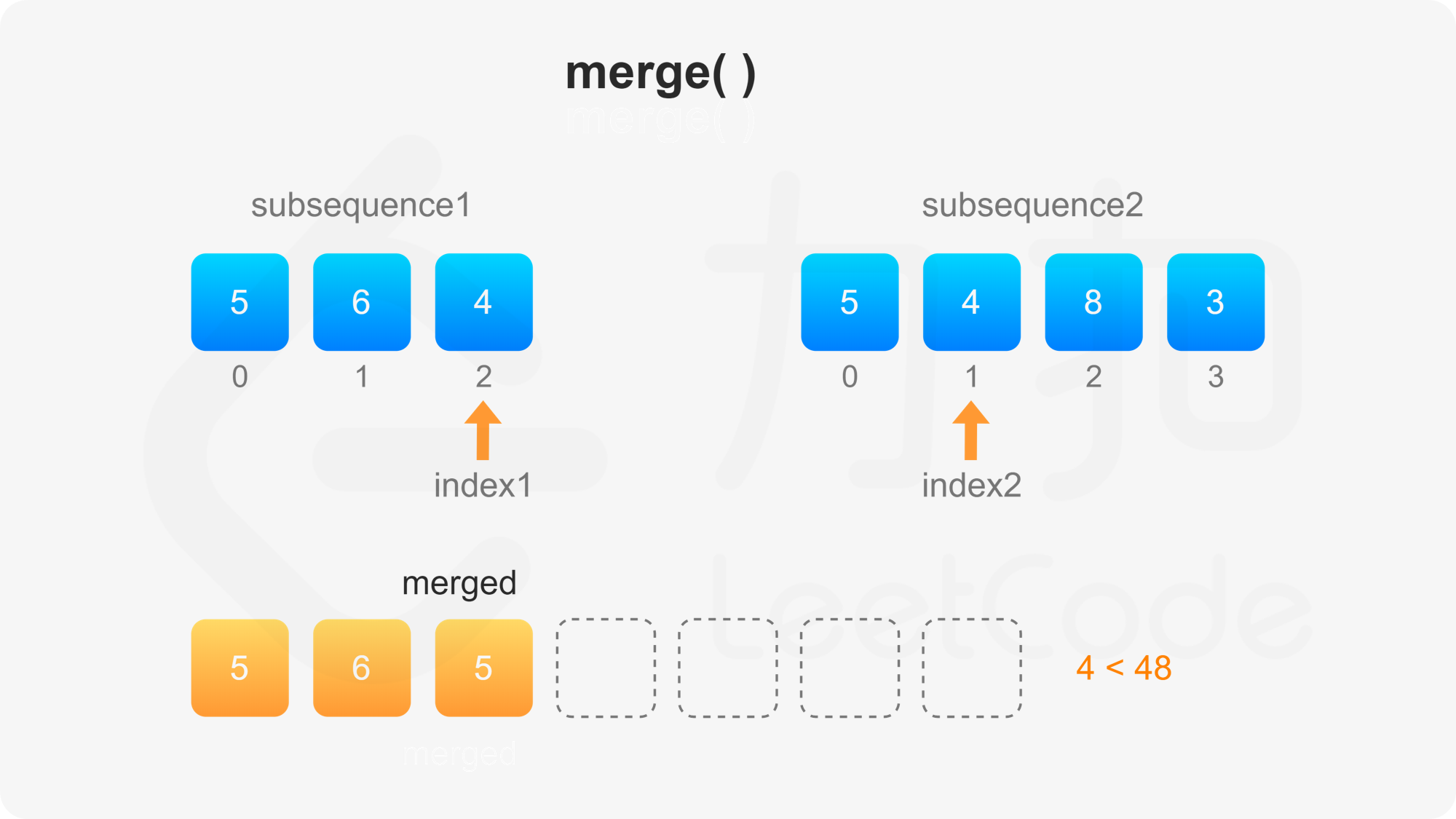 ,
, ,
, ,
, ,
, ,
, >
>