0322-零钱兑换

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

你可以认为每种硬币的数量是无限的。

示例 1：

**输入：** coins = [1, 2, 5], amount = 11
**输出：**3 
**解释：** 11 = 5 + 5 + 1

示例 2：

**输入：** coins = [2], amount = 3
**输出：** -1

示例 3：

**输入：** coins = [1], amount = 0
**输出：** 0

提示：

1 <= coins.length <= 12
1 <= coins[i] <= 231 - 1
0 <= amount <= 104

前言

该问题可建模为以下优化问题：

$$\min_{x} \sum_{i=0}^{n - 1} x_i \ \text{subject to} \sum_{i=0}^{n - 1} x_i \times c_i = S$$

其中，$S$ 是总金额，$c_i$ 是第 $i$ 枚硬币的面值，$x_i$ 是面值为 $c_i$ 的硬币数量，由于 $x_i \times c_i$ 不能超过总金额 $S$，可以得出 $x_i$ 最多不会超过 $\frac{S}{c_i，所以 $x_i$ 的取值范围为 $[{0, \frac{S}{c_i}}]$。

一个简单的解决方案是通过回溯的方法枚举每个硬币数量子集 $[x_0\dots\ x_{n - 1}]$，针对给定的子集计算它们组成的金额数，如果金额数为 $S$，则记录返回合法硬币总数的最小值，反之返回 $-1$。

该做法的时间复杂度为 $O(S^n)$，会超出时间限制，因此必须加以优化。

方法一：记忆化搜索

我们能改进上面的指数时间复杂度的解吗？当然可以，利用动态规划，我们可以在多项式的时间范围内求解。首先，我们定义：

$F(S)$：组成金额 $S$ 所需的最少硬币数量
$[c_{0}\ldots c_{n-1}]$ ：可选的 $n$ 枚硬币面额值

我们注意到这个问题有一个最优的子结构性质，这是解决动态规划问题的关键。最优解可以从其子问题的最优解构造出来。如何将问题分解成子问题？假设我们知道 $F(S)$，即组成金额 $S$ 最少的硬币数，最后一枚硬币的面值是 $C$。那么由于问题的最优子结构，转移方程应为：
$$
F(S) = F(S - C) + 1
$$

但我们不知道最后一枚硬币的面值是多少，所以我们需要枚举每个硬币面额值 $c_0, c_1, c_2 \ldots c_{n -1 并选择其中的最小值。下列递推关系成立：

$$
F(S) = \min_{i=0 … n-1}{ F(S - c_i) } + 1 \ \text{subject to} \ \ S-c_i \geq 0
$$
$$
F(S) = 0 \ , \text{when} \ S = 0
$$
$$
F(S) = -1 \ , \text{when} \ n = 0
$$

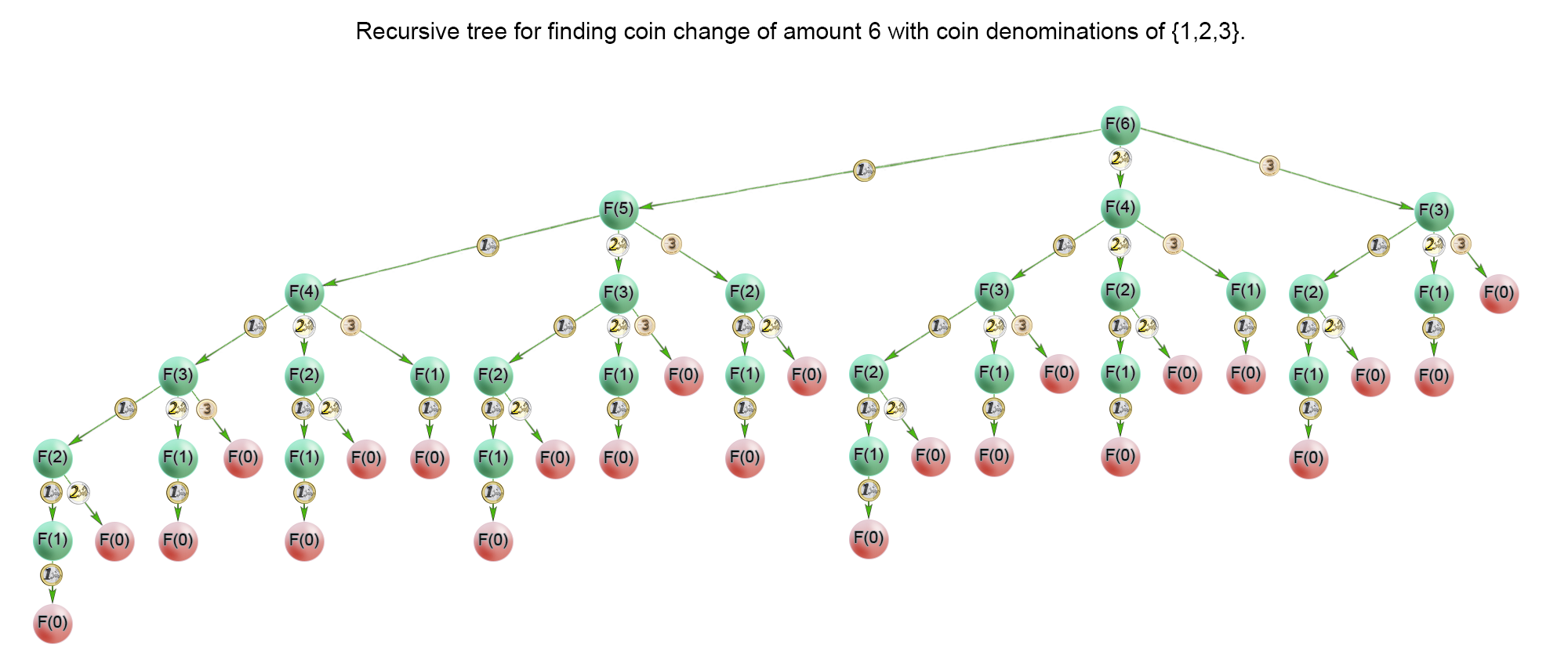
在上面的递归树中，我们可以看到许多子问题被多次计算。例如，$F(1)$ 被计算了 $13$ 次。为了避免重复的计算，我们将每个子问题的答案存在一个数组中进行记忆化，如果下次还要计算这个问题的值直接从数组中取出返回即可，这样能保证每个子问题最多只被计算一次。

[sol1-C++]class Solution {
    vector<int>count;
    int dp(vector<int>& coins, int rem) {
        if (rem < 0) return -1;
        if (rem == 0) return 0;
        if (count[rem - 1] != 0) return count[rem - 1];
        int Min = INT_MAX;
        for (int coin:coins) {
            int res = dp(coins, rem - coin);
            if (res >= 0 && res < Min) {
                Min = res + 1;
            }
        }
        count[rem - 1] = Min == INT_MAX ? -1 : Min;
        return count[rem - 1];
    }
public:
    int coinChange(vector<int>& coins, int amount) {
        if (amount < 1) return 0;
        count.resize(amount);
        return dp(coins, amount);
    }
};

[sol1-Java]public class Solution {
    public int coinChange(int[] coins, int amount) {
        if (amount < 1) {
            return 0;
        }
        return coinChange(coins, amount, new int[amount]);
    }

    private int coinChange(int[] coins, int rem, int[] count) {
        if (rem < 0) {
            return -1;
        }
        if (rem == 0) {
            return 0;
        }
        if (count[rem - 1] != 0) {
            return count[rem - 1];
        }
        int min = Integer.MAX_VALUE;
        for (int coin : coins) {
            int res = coinChange(coins, rem - coin, count);
            if (res >= 0 && res < min) {
                min = 1 + res;
            }
        }
        count[rem - 1] = (min == Integer.MAX_VALUE) ? -1 : min;
        return count[rem - 1];
    }
}

[sol1-Python3]class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        @functools.lru_cache(amount)
        def dp(rem) -> int:
            if rem < 0: return -1
            if rem == 0: return 0
            mini = int(1e9)
            for coin in self.coins:
                res = dp(rem - coin)
                if res >= 0 and res < mini:
                    mini = res + 1
            return mini if mini < int(1e9) else -1

        self.coins = coins
        if amount < 1: return 0
        return dp(amount)

复杂度分析

时间复杂度：$O(Sn)$，其中 $S$ 是金额，$n$ 是面额数。我们一共需要计算 $S$ 个状态的答案，且每个状态 $F(S)$ 由于上面的记忆化的措施只计算了一次，而计算一个状态的答案需要枚举 $n$ 个面额值，所以一共需要 $O(Sn)$ 的时间复杂度。
空间复杂度：$O(S)$，我们需要额外开一个长为 $S$ 的数组来存储计算出来的答案 $F(S)$ 。

方法二：动态规划

算法

我们采用自下而上的方式进行思考。仍定义 $F(i)$ 为组成金额 $i$ 所需最少的硬币数量，假设在计算 $F(i)$ 之前，我们已经计算出 $F(0)-F(i-1)$ 的答案。则 $F(i)$ 对应的转移方程应为

$$F(i)=\min_{j=0 \ldots n-1}{F(i -c_j)} + 1$$

其中 $c_j$ 代表的是第 $j$ 枚硬币的面值，即我们枚举最后一枚硬币面额是 $c_j$，那么需要从 $i-c_j$ 这个金额的状态 $F(i-c_j)$ 转移过来，再算上枚举的这枚硬币数量 $1$ 的贡献，由于要硬币数量最少，所以 $F(i)$ 为前面能转移过来的状态的最小值加上枚举的硬币数量 $1$ 。

例子1：假设

coins = [1, 2, 5], amount = 11

则，当 $i==0$ 时无法用硬币组成，为 0 。当 $i<0$ 时，忽略 $F(i)$

F(i)	最小硬币数量
F(0)	0 //金额为0不能由硬币组成
F(1)	1 //$F(1)=min(F(1-1),F(1-2),F(1-5))+1=1$
F(2)	1 //$F(2)=min(F(2-1),F(2-2),F(2-5))+1=1$
F(3)	2 //$F(3)=min(F(3-1),F(3-2),F(3-5))+1=2$
F(4)	2 //$F(4)=min(F(4-1),F(4-2),F(4-5))+1=2$
…	…
F(11)	3 //$F(11)=min(F(11-1),F(11-2),F(11-5))+1=3$
我们可以看到问题的答案是通过子问题的最优解得到的。

例子2：假设

coins = [1, 2, 3], amount = 6

{:width=300}

在上图中，可以看到：
$$
\begin{aligned}
F(3) &= \min({F(3- c_1), F(3-c_2), F(3-c_3)}) + 1 \
&= \min({F(3- 1), F(3-2), F(3-3)}) + 1 \
&= \min({F(2), F(1), F(0)}) + 1 \
&= \min({1, 1, 0}) + 1 \
&= 1
\end{aligned}
$$

[sol2-C++]class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        int Max = amount + 1;
        vector<int> dp(amount + 1, Max);
        dp[0] = 0;
        for (int i = 1; i <= amount; ++i) {
            for (int j = 0; j < (int)coins.size(); ++j) {
                if (coins[j] <= i) {
                    dp[i] = min(dp[i], dp[i - coins[j]] + 1);
                }
            }
        }
        return dp[amount] > amount ? -1 : dp[amount];
    }
};

[sol2-Java]public class Solution {
    public int coinChange(int[] coins, int amount) {
        int max = amount + 1;
        int[] dp = new int[amount + 1];
        Arrays.fill(dp, max);
        dp[0] = 0;
        for (int i = 1; i <= amount; i++) {
            for (int j = 0; j < coins.length; j++) {
                if (coins[j] <= i) {
                    dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1);
                }
            }
        }
        return dp[amount] > amount ? -1 : dp[amount];
    }
}

[sol2-Python3]class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        dp = [float('inf')] * (amount + 1)
        dp[0] = 0
        
        for coin in coins:
            for x in range(coin, amount + 1):
                dp[x] = min(dp[x], dp[x - coin] + 1)
        return dp[amount] if dp[amount] != float('inf') else -1 

复杂度分析

时间复杂度：$O(Sn)$，其中 $S$ 是金额，$n$ 是面额数。我们一共需要计算 $O(S)$ 个状态，$S$ 为题目所给的总金额。对于每个状态，每次需要枚举 $n$ 个面额来转移状态，所以一共需要 $O(Sn)$ 的时间复杂度。
空间复杂度：$O(S)$。数组 dp 需要开长度为总金额 $S$ 的空间。