0375-猜数字大小 II

我们正在玩一个猜数游戏，游戏规则如下：

1. 我从 1 ** ** 到 n 之间选择一个数字。
2. 你来猜我选了哪个数字。
3. 如果你猜到正确的数字，就会 赢得游戏 。
4. 如果你猜错了，那么我会告诉你，我选的数字比你的 更大或者更小 ，并且你需要继续猜数。
5. 每当你猜了数字 x 并且猜错了的时候，你需要支付金额为 x 的现金。如果你花光了钱，就会 输掉游戏 。

给你一个特定的数字 n ，返回能够 确保你获胜 的最小现金数， 不管我选择那个数字 。

示例 1：

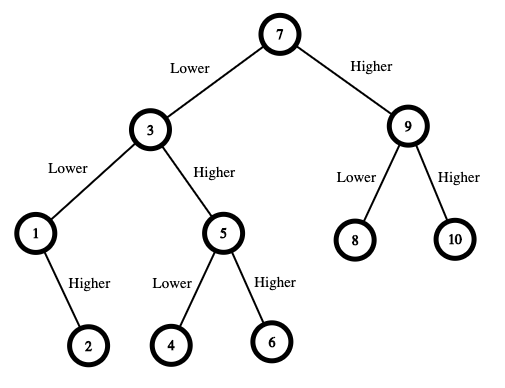
**输入：** n = 10
**输出：** 16
**解释：** 制胜策略如下：
- 数字范围是 [1,10] 。你先猜测数字为 7 。
    - 如果这是我选中的数字，你的总费用为 $0 。否则，你需要支付 $7 。
    - 如果我的数字更大，则下一步需要猜测的数字范围是 [8,10] 。你可以猜测数字为 9 。
        - 如果这是我选中的数字，你的总费用为 $7 。否则，你需要支付 $9 。
        - 如果我的数字更大，那么这个数字一定是 10 。你猜测数字为 10 并赢得游戏，总费用为 $7 + $9 = $16 。
        - 如果我的数字更小，那么这个数字一定是 8 。你猜测数字为 8 并赢得游戏，总费用为 $7 + $9 = $16 。
    - 如果我的数字更小，则下一步需要猜测的数字范围是 [1,6] 。你可以猜测数字为 3 。
        - 如果这是我选中的数字，你的总费用为 $7 。否则，你需要支付 $3 。
        - 如果我的数字更大，则下一步需要猜测的数字范围是 [4,6] 。你可以猜测数字为 5 。
            - 如果这是我选中的数字，你的总费用为 $7 + $3 = $10 。否则，你需要支付 $5 。
            - 如果我的数字更大，那么这个数字一定是 6 。你猜测数字为 6 并赢得游戏，总费用为 $7 + $3 + $5 = $15 。
            - 如果我的数字更小，那么这个数字一定是 4 。你猜测数字为 4 并赢得游戏，总费用为 $7 + $3 + $5 = $15 。
        - 如果我的数字更小，则下一步需要猜测的数字范围是 [1,2] 。你可以猜测数字为 1 。
            - 如果这是我选中的数字，你的总费用为 $7 + $3 = $10 。否则，你需要支付 $1 。
            - 如果我的数字更大，那么这个数字一定是 2 。你猜测数字为 2 并赢得游戏，总费用为 $7 + $3 + $1 = $11 。
在最糟糕的情况下，你需要支付 $16 。因此，你只需要 $16 就可以确保自己赢得游戏。

示例 2：

**输入：** n = 1
**输出：** 0
**解释：** 只有一个可能的数字，所以你可以直接猜 1 并赢得游戏，无需支付任何费用。

示例 3：

**输入：** n = 2
**输出：** 1
**解释：** 有两个可能的数字 1 和 2 。
- 你可以先猜 1 。
    - 如果这是我选中的数字，你的总费用为 $0 。否则，你需要支付 $1 。
    - 如果我的数字更大，那么这个数字一定是 2 。你猜测数字为 2 并赢得游戏，总费用为 $1 。
最糟糕的情况下，你需要支付 $1 。

提示：

• 1 <= n <= 200

方法一：动态规划

为了将支付的金额最小化，除了需要将每次支付的金额控制在较低值以外，还需要在猜数字的过程中缩小所选数字的范围。当猜了数字 $x$ 并且猜错时，会知道 $x$ 比所选数字大还是小。如果 $x$ 比所选数字大，则任何比 $x$ 大的数字一定都比所选数字大，因此应该在比 $x$ 小的数字中继续猜数字。如果 $x$ 比所选数字小，同理可知应该在比 $x$ 大的数字中继续猜数字。

用 $f(i, j)$ 表示在范围 $[i, j]$ 内确保胜利的最少金额，目标是计算 $f(1, n)$。

假设第一次猜的数字是 $x$ 并且猜错，则需要支付金额 $x$，当 $x$ 大于所选数字时，为了确保胜利还需要支付的金额是 $f(1, x - 1)$，当 $x$ 小于所选数字时，为了确保胜利还需要支付的金额是 $f(x + 1, n)$。为了在任何情况下都能确保胜利，应考虑最坏情况，计算 $f(1, n)$ 时应取上述两者的最大值：$f(1, n) = x + \max(f(1, x - 1), f(x + 1, n))$。

为了将确保胜利的金额最小化，需要遍历从 $1$ 到 $n$ 的所有可能的 $x$，使得 $f(1, n)$ 的值最小：

$$
f(1, n) = \min\limits_{1 \le x \le n} {x + \max(f(1, x - 1), f(x + 1, n))}
$$

由于 $f(1, x - 1)$ 和 $f(x + 1, n)$ 都是比原始问题 $f(1, n)$ 规模更小的问题，因此可以使用动态规划的方法求解。

动态规划的状态为 $f(i, j)$，表示在范围 $[i, j]$ 内确保胜利的最少金额。

当 $i = j$ 时范围 $[i, j]$ 只包含 $1$ 个数字，所选数字一定是范围内的唯一的数字，不存在猜错的情况，因此 $f(i, j) = 0$；当 $i > j$ 时范围 $[i, j]$ 不存在，因此 $f(i, j) = 0$。综合上述两种情况可知，动态规划的边界情况是：当 $i \ge j$ 时，$f(i, j) = 0$。

当 $i < j$ 时，在范围 $[i, j]$ 内第一次猜的数字可能是该范围内的任何一个数字。在第一次猜的数字是 $k$ 的情况下（$i \le k \le j$），在范围 $[i, j]$ 内确保胜利的最少金额是 $k + \max(f(i, k - 1), f(k + 1, j))$。需要遍历全部可能的 $k$ 找到在范围 $[i, j]$ 内确保胜利的最少金额，因此状态转移方程如下：

$$
f(i, j) = \min\limits_{i \le k \le j} {k + \max(f(i, k - 1), f(k + 1, j))}
$$

由于状态转移方程为根据规模小的子问题计算规模大的子问题，因此计算子问题的顺序为先计算规模小的子问题，后计算规模大的子问题，需要注意循环遍历的方向。

实现方面，创建行数和列数都是 $n + 1$ 的二维数组 $f$，其中 $f[i][j]$ 即为状态 $f(i, j)$。在根据状态转移方程计算时需要注意下标的边界问题，当 $j = n$ 时，如果 $k = j$ 则 $k + 1 > n$，此时 $f[k][j]$ 会出现下标越界。为了避免出现下标越界，计算 $f[i][j]$ 的方法是：首先令 $f[i][j] = j + f[i][j - 1]$，然后遍历 $i \le k < j$ 的每个 $k$，更新 $f[i][j]$ 的值。

[sol1-Java]

class Solution {
    public int getMoneyAmount(int n) {
        int[][] f = new int[n + 1][n + 1];
        for (int i = n - 1; i >= 1; i--) {
            for (int j = i + 1; j <= n; j++) {
                f[i][j] = j + f[i][j - 1];
                for (int k = i; k < j; k++) {
                    f[i][j] = Math.min(f[i][j], k + Math.max(f[i][k - 1], f[k + 1][j]));
                }
            }
        }
        return f[1][n];
    }
}

[sol1-C#]

public class Solution {
    public int GetMoneyAmount(int n) {
        int[,] f = new int[n + 1, n + 1];
        for (int i = n - 1; i >= 1; i--) {
            for (int j = i + 1; j <= n; j++) {
                f[i, j] = j + f[i, j - 1];
                for (int k = i; k < j; k++) {
                    f[i, j] = Math.Min(f[i, j], k + Math.Max(f[i, k - 1], f[k + 1, j]));
                }
            }
        }
        return f[1, n];
    }
}

[sol1-C++]

class Solution {
public:
    int getMoneyAmount(int n) {
        vector<vector<int>> f(n+1,vector<int>(n+1));
        for (int i = n - 1; i >= 1; i--) {
            for (int j = i + 1; j <= n; j++) {
                f[i][j] = j + f[i][j - 1];
                for (int k = i; k < j; k++) {
                    f[i][j] = min(f[i][j], k + max(f[i][k - 1], f[k + 1][j]));
                }
            }
        }
        return f[1][n];
    }
};

[sol1-Golang]

func getMoneyAmount(n int) int {
    f := make([][]int, n+1)
    for i := range f {
        f[i] = make([]int, n+1)
    }
    for i := n - 1; i >= 1; i-- {
        for j := i + 1; j <= n; j++ {
            f[i][j] = j + f[i][j-1]
            for k := i; k < j; k++ {
                cost := k + max(f[i][k-1], f[k+1][j])
                if cost < f[i][j] {
                    f[i][j] = cost
                }
            }
        }
    }
    return f[1][n]
}

func max(a, b int) int {
    if b > a {
        return b
    }
    return a
}

[sol1-Python3]

class Solution:
    def getMoneyAmount(self, n: int) -> int:
        f = [[0] * (n + 1) for _ in range(n + 1)]
        for i in range(n - 1, 0, -1):
            for j in range(i + 1, n + 1):
                f[i][j] = j + f[i][j - 1]
                for k in range (i, j):
                    f[i][j] = min(f[i][j], k + max(f[i][k - 1], f[k + 1][j]))
        return f[1][n]

[sol1-JavaScript]

var getMoneyAmount = function(n) {
    const f = new Array(n + 1).fill(0).map(() => new Array(n + 1).fill(0));
    for (let i = n - 1; i >= 1; i--) {
        for (let j = i + 1; j <= n; j++) {
            f[i][j] = j + f[i][j - 1];
            for (let k = i; k < j; k++) {
                f[i][j] = Math.min(f[i][j], k + Math.max(f[i][k - 1], f[k + 1][j]));
            }
        }
    }
    return f[1][n];
};

复杂度分析

• 时间复杂度：$O(n^3)$，其中 $n$ 是给定的参数。状态数量是 $O(n^2)$，需要对每个状态使用 $O(n)$ 的时间计算状态值，因此总时间复杂度是 $O(n^3)$。

• 空间复杂度：$O(n^2)$。需要创建 $n + 1$ 行 $n + 1$ 列的二维数组 $f$。