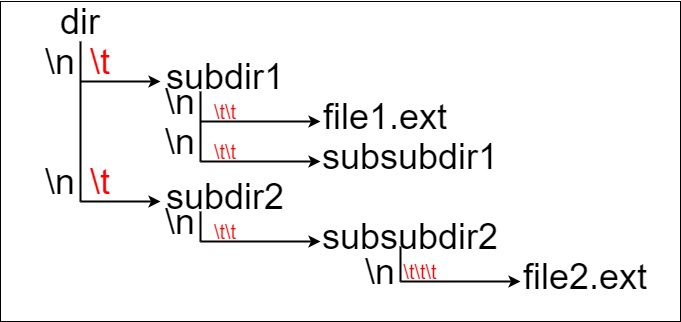
假设有一个同时存储文件和目录的文件系统。下图展示了文件系统的一个示例:
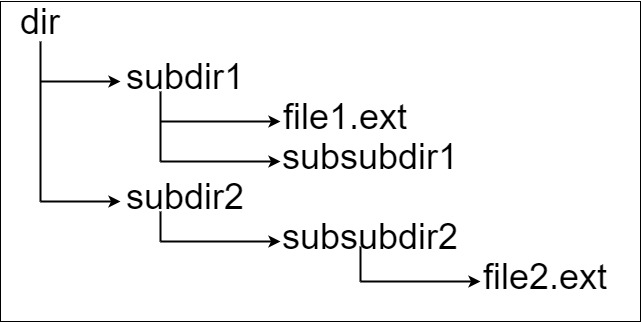
这里将 dir 作为根目录中的唯一目录。dir 包含两个子目录 subdir1 和 subdir2 。subdir1 包含文件file1.ext 和子目录 subsubdir1;subdir2 包含子目录 subsubdir2,该子目录下包含文件file2.ext 。
在文本格式中,如下所示(⟶表示制表符):
dir
⟶ subdir1
⟶ ⟶ file1.ext
⟶ ⟶ subsubdir1
⟶ subdir2
⟶ ⟶ subsubdir2
⟶ ⟶ ⟶ file2.ext
如果是代码表示,上面的文件系统可以写为"dir\n\tsubdir1\n\t\tfile1.ext\n\t\tsubsubdir1\n\tsubdir2\n\t\tsubsubdir2\n\t\t\tfile2.ext"'\n' 和 '\t' 分别是换行符和制表符。
文件系统中的每个文件和文件夹都有一个唯一的 绝对路径 ,即必须打开才能到达文件/目录所在位置的目录顺序,所有路径用 '/'file2.ext 的 绝对路径 是 "dir/subdir2/subsubdir2/file2.ext"name.extension 的格式,其中 name 和extension由字母、数字和/或空格组成。
给定一个以上述格式表示文件系统的字符串 input ,返回文件系统中 指向 文件 的 最长绝对路径 的长度 。0。
示例 1:
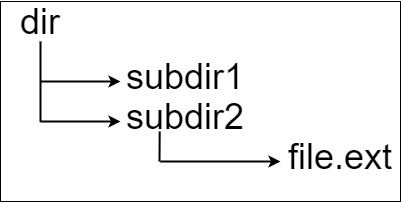
**输入:** input = "dir\n\tsubdir1\n\tsubdir2\n\t\tfile.ext"
**输出:** 20
**解释:** 只有一个文件,绝对路径为 "dir/subdir2/file.ext" ,路径长度 20
示例 2:
**输入:** input = "dir\n\tsubdir1\n\t\tfile1.ext\n\t\tsubsubdir1\n\tsubdir2\n\t\tsubsubdir2\n\t\t\tfile2.ext"
**输出:** 32
**解释:** 存在两个文件:
"dir/subdir1/file1.ext" ,路径长度 21
"dir/subdir2/subsubdir2/file2.ext" ,路径长度 32
返回 32 ,因为这是最长的路径
示例 3:
**输入:** input = "a"
**输出:** 0
**解释:** 不存在任何文件
示例 4:
**输入:** input = "file1.txt\nfile2.txt\nlongfile.txt"
**输出:** 12
**解释:** 根目录下有 3 个文件。
因为根目录中任何东西的绝对路径只是名称本身,所以答案是 "longfile.txt" ,路径长度为 12
提示:
1 <= input.length <= 104input 可能包含小写或大写的英文字母,一个换行符 '\n',一个制表符 '\t',一个点 '.',一个空格 ' ',和数字。
方法一:栈 思路与算法
题目中需求出文件系统中文件绝对路径的最大长度。首先观察文件绝对路径的特征,文件名一定包含 .',此时文件的绝对路径为 x/y/.../a.b,其中 x,y 代表文件夹的名称,a.b 代表文件名。我们可以观察到文件系统实际为树形结构,文件一定为树中的叶子节点,文件夹可以为根节点也可以为叶子节点,题目中给定的文件系统字符串实际为树按照前序遍历的结果,连续的 \verb||t’ 的个数代表当前节点的深度,相邻的文件名之间都以 `\verb||n’ 进行隔开。
假设当前的路径为 x/y/z,其中 x,y,z 的文件名长度为分别为 $l_x,l_y,l_z$,则路径 x, x/y, x/y/z 的长度分别为 $l_x, l_x + l_y + 1, l_x + l_y + l_z + 2$。我们利用栈保存当前已遍历路径的长度,栈中元素的个数即为当前路径的深度,栈顶元素即为当前路径的长度。设根节点的深度为 $1$,字符串中连续的 `\verb||t’ 的个数加 $1$ 即为当前节点的深度 depth,设当前节点的文件名为 q,当前节点的文件名长度为 $l_p$,根据节点深度 depth 有以下判断:
如果当前节点的深度大于当前路径的深度,则表明当前节点为栈顶节点的孩子节点,设当前栈顶节点的长度为 t,栈顶节点的路径为 p,则此时当前文件的路径应该为 p/q,则此时当前文件的路径长度为 $t + l_p + 1$。
如果当前节点的深度小于当前路径的深度,则表明当前节点并不是栈顶节点的孩子节点,按照先序遍历的顺序,则此时需要进行回退直到栈顶节点为当前节点的父亲节点,然后再求出当前节点的路径与长度。
由于题目只需要求出文件的长度即可,因此我们在实际运算中在栈中不需要保存完整的路径名称,只需要保存每个路径的长度即可。检测当前节点的文件名的长度并标记当前的文件名是文件还是文件夹,如果当前的字符串为文件,则求出当前文件绝对路径的长度。遍历所有可能的文件长度,即可找到文件绝对路径的最大长度。
代码
[sol1-Python3] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class Solution : def lengthLongestPath (self, input : str ) -> int : st = [] ans, i, n = 0 , 0 , len (input ) while i < n: depth = 1 while i < n and input [i] == '\t' : depth += 1 i += 1 length, isFile = 0 , False while i < n and input [i] != '\n' : if input [i] == '.' : isFile = True length += 1 i += 1 i += 1 while len (st) >= depth: st.pop() if st: length += st[-1 ] + 1 if isFile: ans = max (ans, length) else : st.append(length) return ans
[sol1-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 class Solution { public int lengthLongestPath (String input) { int n = input.length(); int pos = 0 ; int ans = 0 ; Deque<Integer> stack = new ArrayDeque <Integer>(); while (pos < n) { int depth = 1 ; while (pos < n && input.charAt(pos) == '\t' ) { pos++; depth++; } boolean isFile = false ; int len = 0 ; while (pos < n && input.charAt(pos) != '\n' ) { if (input.charAt(pos) == '.' ) { isFile = true ; } len++; pos++; } pos++; while (stack.size() >= depth) { stack.pop(); } if (!stack.isEmpty()) { len += stack.peek() + 1 ; } if (isFile) { ans = Math.max(ans, len); } else { stack.push(len); } } return ans; } }
[sol1-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 class Solution {public : int lengthLongestPath (string input) int n = input.size (); int pos = 0 ; int ans = 0 ; stack<int > st; while (pos < n) { int depth = 1 ; while (pos < n && input[pos] == '\t' ) { pos++; depth++; } int len = 0 ; bool isFile = false ; while (pos < n && input[pos] != '\n' ) { if (input[pos] == '.' ) { isFile = true ; } len++; pos++; } pos++; while (st.size () >= depth) { st.pop (); } if (!st.empty ()) { len += st.top () + 1 ; } if (isFile) { ans = max (ans, len); } else { st.emplace (len); } } return ans; } };
[sol1-C#] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 public class Solution { public int LengthLongestPath (string input int n = input.Length; int pos = 0 ; int ans = 0 ; Stack<int > stack = new Stack<int >(); while (pos < n) { int depth = 1 ; while (pos < n && input[pos] == '\t' ) { pos++; depth++; } bool isFile = false ; int len = 0 ; while (pos < n && input[pos] != '\n' ) { if (input[pos] == '.' ) { isFile = true ; } len++; pos++; } pos++; while (stack.Count >= depth) { stack.Pop(); } if (stack.Count > 0 ) { len += stack.Peek() + 1 ; } if (isFile) { ans = Math.Max(ans, len); } else { stack.Push(len); } } return ans; } }
[sol1-C] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 #define MAX(a, b) ((a) > (b) ? (a) : (b)) int lengthLongestPath (char * input) { int n = strlen (input); int pos = 0 ; int ans = 0 ; int * stack = (int *)malloc (sizeof (int ) * n); int top = 0 ; while (pos < n) { int depth = 1 ; while (pos < n && input[pos] == '\t' ) { pos++; depth++; } bool isFile = false ; int len = 0 ; while (pos < n && input[pos] != '\n' ) { if (input[pos] == '.' ) { isFile = true ; } len++; pos++; } pos++; while (top >= depth) { top--; } if (top > 0 ) { len += stack [top - 1 ] + 1 ; } if (isFile) { ans = MAX(ans, len); } else { stack [top++] = len; } } free (stack ); return ans; }
[sol1-JavaScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 var lengthLongestPath = function (input ) { const n = input.length ; let pos = 0 ; let ans = 0 ; const stack = []; while (pos < n) { let depth = 1 ; while (pos < n && input[pos] === '\t' ) { pos++; depth++; } let isFile = false ; let len = 0 ; while (pos < n && input[pos] !== '\n' ) { if (input[pos] === '.' ) { isFile = true ; } len++; pos++; } pos++; while (stack.length >= depth) { stack.pop (); } if (stack.length ) { len += stack[stack.length - 1 ] + 1 ; } if (isFile) { ans = Math .max (ans, len); } else { stack.push (len); } } return ans; };
[sol1-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 func lengthLongestPath (input string ) int ) { st := []int {} for i, n := 0 , len (input); i < n; { depth := 1 for ; i < n && input[i] == '\t' ; i++ { depth++ } length, isFile := 0 , false for ; i < n && input[i] != '\n' ; i++ { if input[i] == '.' { isFile = true } length++ } i++ for len (st) >= depth { st = st[:len (st)-1 ] } if len (st) > 0 { length += st[len (st)-1 ] + 1 } if isFile { ans = max(ans, length) } else { st = append (st, length) } } return } func max (a, b int ) int { if b > a { return b } return a }
复杂度分析
方法二:遍历 思路与算法
假设当前的路径为 x/y/z,其中 x,y,z 的文件名长度为分别为 $l_x,l_y,l_z$,则路径 x, x/y, x/y/z 的长度分别为 $l_x, l_x + l_y + 1, l_x + l_y + l_z + 2$。我们用 level}[i]$ 保存当前已遍历路径中第 $i$ 层目录的长度。设根目录为第 $1$ 层,字符串中连续的 `\verb||t’ 的个数加 $1$ 即为当前路径的层次深度 depth,设当前节点的文件名为 p,当前节点的文件名长度为 $l_p$,根据当前文件的层次深度 depth 有以下判断:
当前文件绝对路径也就等于当前路径中第 depth} - 1$ 层的绝对路径加上 /',然后再加上当前的文件名,当前文件绝对路径的长度也就等于 level}[\textit{depth} - 1] + 1 + l_p$。特殊情况需要处理,当前为根目录时,不需要添加额外的 /‘。如果当前文件名为文件夹时,则需要更新当前第 depth 层的路径长度。
由于每次目录按照向下遍历时,是按照层级目录往下进行遍历的,即每次只能遍历完第 $i$ 层目录,才能遍历到第 $i+1$ 层目录,因此我们在向下进行遍历第 $i$ 层目录时,实际上前 $i-1$ 层的目录路径不会发生改变。当从 $i$ 层目录回退到第 $j$ 层时,$i > j$,此时前 $i-1$ 层绝对路径是保持不变的,因此可以直接利用已经保存的前 $i-1$ 层的绝对路径长度。
由于题目只需要求出文件的长度即可,因此我们在实际运算中不需要保存完整的路径名称,只需要保存每个路径的长度即可。检测当前节点的文件名的长度并标记当前的文件名是文件还是文件夹,如果当前的文件名为文件,则求出当前文件绝对路径的长度。遍历所有可能的文件路径长度,即可找到文件绝对路径的最大长度。
代码
[sol2-Python3] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution : def lengthLongestPath (self, input : str ) -> int : ans, i, n = 0 , 0 , len (input ) level = [0 ] * (n + 1 ) while i < n: depth = 1 while i < n and input [i] == '\t' : depth += 1 i += 1 length, isFile = 0 , False while i < n and input [i] != '\n' : if input [i] == '.' : isFile = True length += 1 i += 1 i += 1 if depth > 1 : length += level[depth - 1 ] + 1 if isFile: ans = max (ans, length) else : level[depth] = length return ans
[sol2-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 class Solution { public int lengthLongestPath (String input) { int n = input.length(); int pos = 0 ; int ans = 0 ; int [] level = new int [n + 1 ]; while (pos < n) { int depth = 1 ; while (pos < n && input.charAt(pos) == '\t' ) { pos++; depth++; } int len = 0 ; boolean isFile = false ; while (pos < n && input.charAt(pos) != '\n' ) { if (input.charAt(pos) == '.' ) { isFile = true ; } len++; pos++; } pos++; if (depth > 1 ) { len += level[depth - 1 ] + 1 ; } if (isFile) { ans = Math.max(ans, len); } else { level[depth] = len; } } return ans; } }
[sol2-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 class Solution {public : int lengthLongestPath (string input) int n = input.size (); int pos = 0 ; int ans = 0 ; vector<int > level (n + 1 ) ; while (pos < n) { int depth = 1 ; while (pos < n && input[pos] == '\t' ) { pos++; depth++; } int len = 0 ; bool isFile = false ; while (pos < n && input[pos] != '\n' ) { if (input[pos] == '.' ) { isFile = true ; } len++; pos++; } pos++; if (depth > 1 ) { len += level[depth - 1 ] + 1 ; } if (isFile) { ans = max (ans, len); } else { level[depth] = len; } } return ans; } };
[sol2-C#] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 public class Solution { public int LengthLongestPath (string input int n = input.Length; int pos = 0 ; int ans = 0 ; int [] level = new int [n + 1 ]; while (pos < n) { int depth = 1 ; while (pos < n && input[pos] == '\t' ) { pos++; depth++; } int len = 0 ; bool isFile = false ; while (pos < n && input[pos] != '\n' ) { if (input[pos] == '.' ) { isFile = true ; } len++; pos++; } pos++; if (depth > 1 ) { len += level[depth - 1 ] + 1 ; } if (isFile) { ans = Math.Max(ans, len); } else { level[depth] = len; } } return ans; } }
[sol2-C] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 #define MAX(a, b) ((a) > (b) ? (a) : (b)) int lengthLongestPath (char * input) { int n = strlen (input); int pos = 0 ; int ans = 0 ; int * level = (int *)malloc (sizeof (int ) * (n + 1 )); memset (level, 0 , sizeof (int ) * (n + 1 )); while (pos < n) { int depth = 1 ; while (pos < n && input[pos] == '\t' ) { pos++; depth++; } bool isFile = false ; int len = 0 ; while (pos < n && input[pos] != '\n' ) { if (input[pos] == '.' ) { isFile = true ; } len++; pos++; } pos++; if (depth > 1 ) { len += level[depth - 1 ] + 1 ; } if (isFile) { ans = MAX(ans, len); } else { level[depth] = len; } } free (level); return ans; }
[sol2-JavaScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 var lengthLongestPath = function (input ) { const n = input.length ; let pos = 0 ; let ans = 0 ; const level = new Array (n + 1 ).fill (0 ); while (pos < n) { let depth = 1 ; while (pos < n && input[pos] === '\t' ) { pos++; depth++; } let len = 0 ; let isFile = false ; while (pos < n && input[pos] !== '\n' ) { if (input[pos] === '.' ) { isFile = true ; } len++; pos++; } pos++; if (depth > 1 ) { len += level[depth - 1 ] + 1 ; } if (isFile) { ans = Math .max (ans, len); } else { level[depth] = len; } } return ans; }
[sol2-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 func lengthLongestPath (input string ) int ) { n := len (input) level := make ([]int , n+1 ) for i := 0 ; i < n; { depth := 1 for ; i < n && input[i] == '\t' ; i++ { depth++ } length, isFile := 0 , false for ; i < n && input[i] != '\n' ; i++ { if input[i] == '.' { isFile = true } length++ } i++ if depth > 1 { length += level[depth-1 ] + 1 } if isFile { ans = max(ans, length) } else { level[depth] = length } } return } func max (a, b int ) int { if b > a { return b } return a }
复杂度分析